基于可变形卷积神经网络的软件漏洞检测算法

林若钦，罗 琼

(广州大学华软软件学院，广东 广州 510990)

1 引言

软件系统广泛应用于各类生产、生活领域中，其开发过程中需要考虑的首要问题就是安全性，软件漏洞既会使资源产生不必要的消耗，也会严重损失应用行业的经济财产[1-2]。漏洞通常比较隐秘，而且与正常的程序数据没有明显差异，想又快又准地找到软件中存在的漏洞并非一件易事，因此，研究一种有效的软件漏洞检测算法具有一定的必要性。

文献[3]为提升开源软件代码质量、消除安全隐患，结合混合深度学习模型，提出一种开源软件漏洞检测方法，依据漏洞库关键点，架构控制流图，提取静态代码片段，经过数字化处理，将代码片段设置成混合深度学习模型输入项，令卷积神经网络成为与特征向量的交互接口，在网络中嵌入门控循环单元，获取门控机制，通过卷积、池化处理，降低特征向量维度，将该特征向量发送至softmax分类器中检测软件漏洞；文献[4]提出的软件漏洞检测Fuzzing样本优化法中，通过剔除软件不接受样本，利用改进的动态规划算法，获取初始样本简化集合，采用改进的simhash与海明距离算法，计算样本传播路径相似度，去除高相似度样本，经过遗传变异异常样本，架构新的测试样本，作为漏洞检测的理想数据。

由于上述方法无法应对软件漏洞变化，所以，本文对文献方法取长补短，提出一种可变形卷积神经网络的软件漏洞检测方法，其创新之处在于利用可变形卷积神经网络的反向传播路径，抑制梯度爆炸与梯度消失等问题发生，凭借激活函数与残差单元，提升训练梯度稳定性，因卷积神经网络中可以实现卷积核共享，网络深度决定着反向传播路径长度，所以，能够大幅降低算法在检测软件漏洞时的内存消耗。

2 基于可变形卷积神经网络的软件漏洞检测

2.1 可变形卷积神经网络

在一个子网络中添加输入的软件漏洞特征U，该子网络由卷积层、全连接层等架构而成，得到定位网络的空间变换参数θ。为获取基于输入特征U坐标方位的输出漏洞特征X坐标点[5]，将空间变换参数θ通过网格生成器变为一个参数化采样网格[6]。

利用双线性插值采样网格生成器的采样点坐标[7]，求解对应软件漏洞特征数值，计算公式如下所示

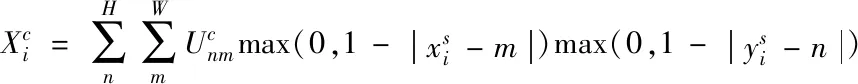
(1)

为取得更加理想的采样效果，在可变形卷积中将偏移量添加至各卷积采样点上。

2.2 软件漏洞检测

基于构建的可变形卷积网络，采用规则的采样网格R，完成输入特征映射x的采样，经过权值ω与采样值做积后，计算所有乘积的总和。可变形卷积神经网络下软件漏洞检测算法以n×n规格的标准卷积核为基础，设定输出漏洞特征X的任意点为p0，基于神经元输出形式的界定，推导出软件漏洞特征点在可变形卷积神经网络下的表达式，如下所示

X(p0)=∑pnω(pn)x(p0+pn)

(2)

式中，采样网格R包含的任意采样点为pn。

规则采样网格R在可变形卷积神经网络中会受到偏移量的变化影响，令偏移量大小与输入层大小相同，通过卷积漏洞偏移，实现采样点优化。因此，将一组满足{Δpn|n=1，2，…，N}的偏移量Δpn代入上式中，得到下列表达式

X(p0)=∑pnω(pn)x(p0+pn+Δpn)

(3)

式中，N=|R|，采样点用pn+Δpn表示。

一般情况下，偏移采样点会在不规则网格中发生偏移，确保采样点坐标始终是一个整数形式存在一定难度，导致偏移量Δpn的取值通常是一个小数，所以，利用双线性插值方法来求解偏移量Δpn，计算公式如下所示

x(p)=∑qG(q，p)x(q)

(4)

式中，偏移量取值为小数时的任意采样点方位用p表示，表达式如下所示

p=p0+pn+Δpn

(5)

特征映射x的各空间方位为q，双线性插值核为函数G(q，p)，采用下列表达式加以描述

G(q，p)=g(qx，px)g(qy，py)

(6)

式中，函数g(qn，pn)的运算规则表达式如下所示

g(qn，pn)=max(0，1-|qn-pn|)

(7)

针对可变形卷积的池化变形形式，其表达式如下所示

(8)

3 软件漏洞检测模拟分析

3.1 实验环境与评估指标

表1所示为实验的相关硬件配置与软件应用环境。

表1 实验环境

实验数据集由CWE-117与CWE-366组成。为确保软件程序正常运行，采用checkmarx处理数据集所含代码数据，人工审核数据标签，并对较长和发生错误截断的样本进行剔除。CWE-117数据集与CWE-366数据集分别是缓冲区溢出漏洞与脆弱性漏洞[8-9]，两数据集混合后含有多个数据特征，检测复杂度较大。实验数据集的具体信息如表2所示。

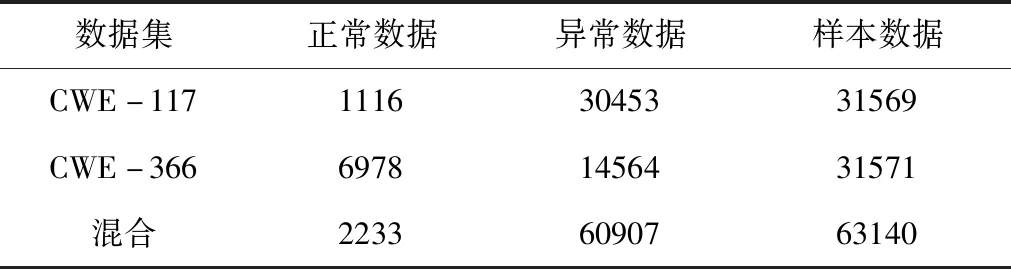
表2 数据集统计表

选用准确率precision、召回率[10]recall以及综合指标F1，评价检测算法性能，各指标界定公式分别如下所示

(9)

(10)

(11)

式中，TP为真正例，表示正确检测的漏洞数量，FP为假正例，表示检测错误的漏洞数量，FN为假负例，表示检测错误的非漏洞数量。

3.2 神经网络层数对检测算法的影响

选取混合数据集作为漏洞检测对象，通过记录递增卷积核尺寸下不同网络层数的指标数据，验证本文算法性能。

当卷积核尺寸取值为2，网络层数不断增加时，本文算法的训练集与测试集损失曲线如图1所示。

图1 卷积核尺寸取2时损失指标

根据图1中的曲线走势可以看出，当训练集与测试集的网络层数增加到7层时，损失最大，训练集的网络层数增加到9层时，损失最小，而测试集其它网络层数所产生的损失较为接近，训练期数过多有可能引发过拟合现象[11-12]。

从图2所示的相同卷积核尺寸下算法准确率与召回率曲线形式可以看出，当网络层数取值7时，准确率与召回率都呈现出较差的水平趋势，而且在训练期数达到一定数量后，两指标数据均有明显下降。

图2 卷积核尺寸取2时准确率与召回率

根据该卷积核尺寸的误报率示意图，如图3所示，发现网络层数为7时，误报率数值有明显增加，但其它层数对算法性能影响不大，训练期数仍会导致过拟合问题发生。

图3 卷积核尺寸取2时误报率

卷积核尺寸取4时不同网络层数的各项指标数据曲线走势分别如图4所示。从训练集与测试集损失曲线图中可以看出，当网络层数增加到6层时，损失最大，其它网络层数所产生的损失相差无几，训练期数不断增加后发生了欠拟合现象，准确率与召回率指标数值也始终处于最低值，其它网络层数的准确率与召回率指标数值较为接近，而误报率指标未受到网络层数与训练期数的太大影响，各网络层数的误报率均不存在显著差异。

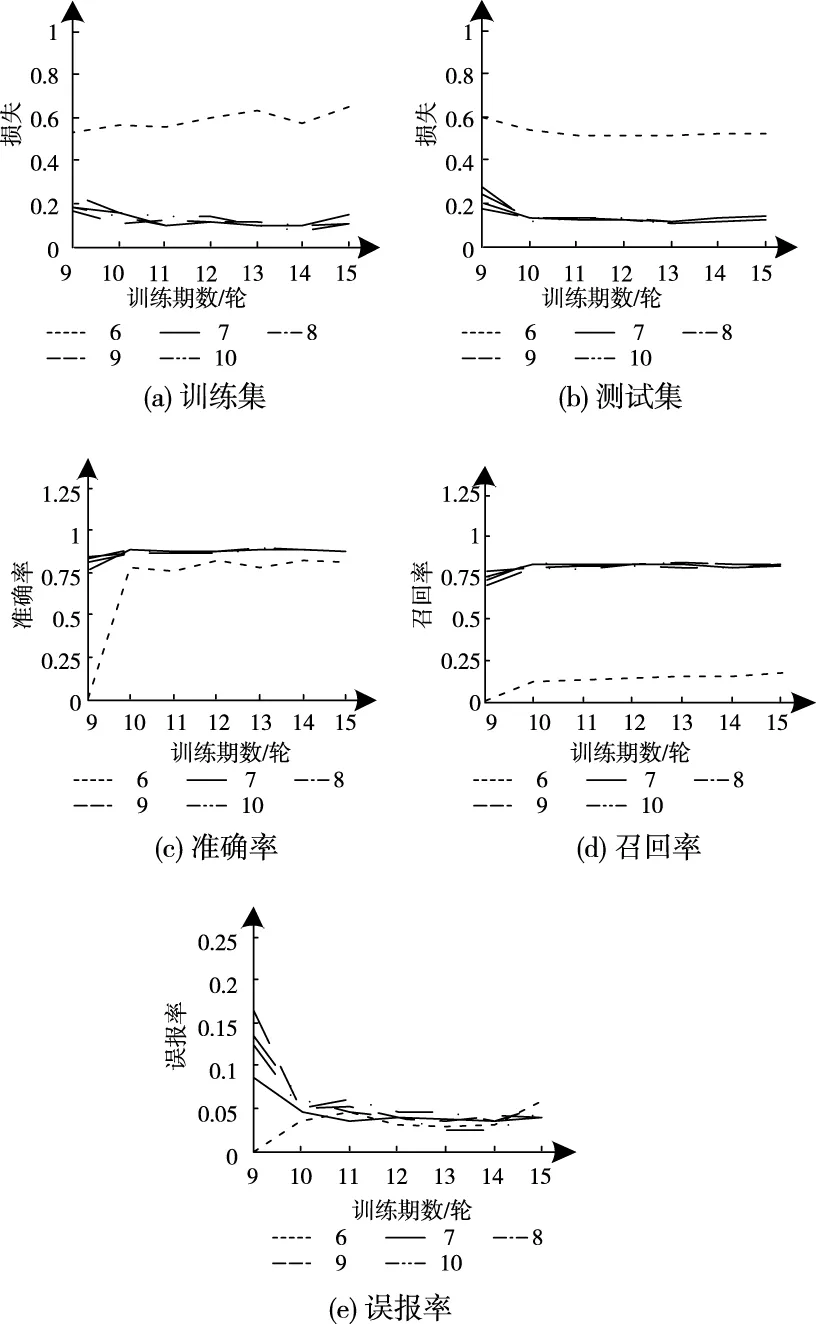
图4 卷积核尺寸取4时各指标曲线图

根据卷积核尺寸取值为6时各网络层数对应的训练集与测试集损失曲线示意图(见图5)可以看出，更深的网络层数并未造成测试集损失的显著下降，但当网络是8层时，出现了欠拟合问题，与前两种卷积核情况不同的是，卷积核尺寸较大导致过拟合临界点提前，在训练达到一定期数时，测试集损失有回弹现象，并逐渐增加提升幅度。

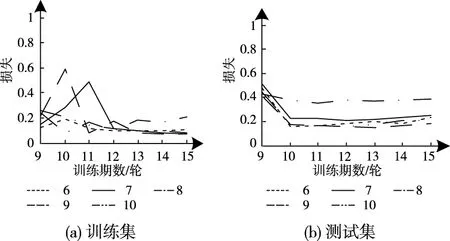
图5 卷积核尺寸取6时损失指标

通过准确率、召回率以及误报率指标曲线(如图6所示)可知，在网络深度相同的情况下，较大尺寸卷积核的网络参数规模大于较小尺寸卷积核的规模，因此，卷积核尺寸较大时的网络劣势相对显著。当训练叠加至13期后，网络的过拟合现象开始突显，准确率、召回率以及误报率指标数据均逐渐上升，网络层数过多将引发过拟合现象提前，这与前几种尺寸的卷积核对应指标情况相符合。

图6 卷积核尺寸取6时其它指标示意图

为进一步验证所得结论，探索基于不同卷积核尺寸与网络层数的感受野尺寸，整理出下列感受野尺寸统计表。

表3 不同卷积核尺寸与网络层数下感受野统计表

根据表3中感受野尺寸可以看出，感受野尺寸与标准序列长度差异较大时，神经网络不具备较好的漏洞检测性能，通过增加网络层数来加深深度，能够有效缩短感受野尺寸与标准序列长度之间的差异，大幅度提升算法的检测性能。结合上述所有实验图表数据后可知，在网络过深导致过拟合现象发生时，网络增加至8层可以对该现象形成一定的抑制优势，训练期数达到15轮后，8层网络的测试集损失、准确率、召回率以及误报率指标明显更具优越性，究其原因是此时的网络拟合能力较弱，不足以引发过拟合现象出现。

基于超参数的综合最佳结果统计表下列各表所示，用fpr表示误报率指标，则综合最佳结果c的界定表达式如下所示：

c=precision+recall-fpr

(12)

经过整理CWE-117、CWE-366两数据集与混合数据集的综合最佳结果，得到各数据集对应的结果统计表，如下所示。通过对比各类型数据集的综合最佳数据结果发现，基于相同规模的网络深度，CWE-366数据集因漏洞较少，所以，具备更理想的综合最佳结果。尽管其它两种数据集漏洞更多，检测难度更大，但根据对应综合最佳结果数据显示，该检测算法仍能够满足实际的漏洞检测需求。

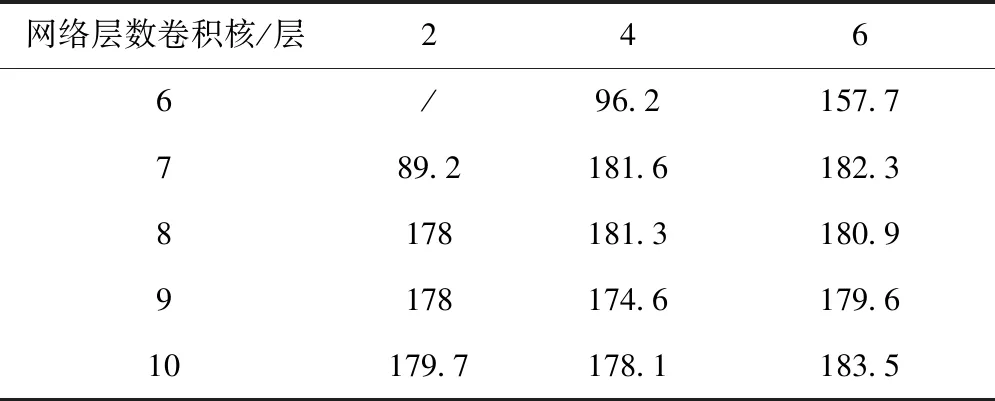
表4 CWE-117数据集综合最佳结果统计表

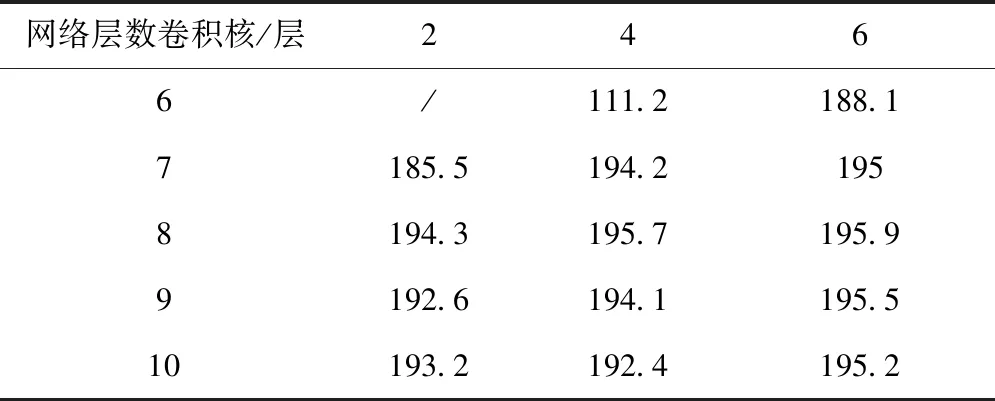
表5 CWE-366数据集综合最佳结果统计表

表6 混合数据集综合最佳结果统计表

为验证算法有效性，分别采用文献[3]、[4]方法对CWE-117数据集、CWE-366数据集以及混合数据集展开漏洞检测，获取各方法的综合最佳结果，将求取的平均值与本文算法结果均值进行对比，如表7所示。

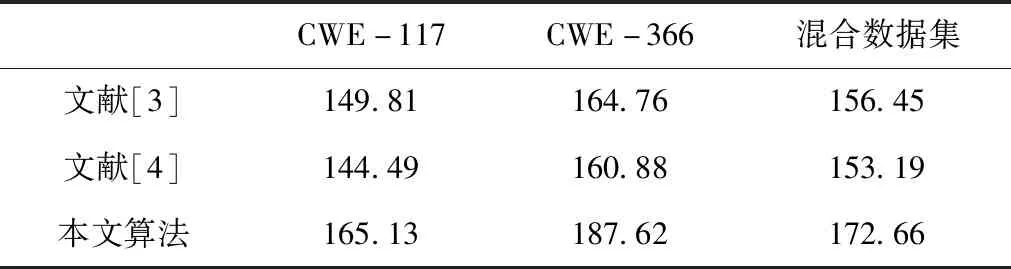
表7 各方法不同种类数据集的综合最佳结果比对表

通过对比各方法基于不同数据集的综合最佳结果可以看出，相对于文献[3]、[4]方法，本文算法的综合最佳结果相对更高，说明在检测各类数据集漏洞的过程中具有较为理想的算法性能，这是因为本文算法采用规则的采样网格与大小同于输入层的偏移量，基于可变形卷积的池化变形形式，利用一样的卷积核进行并行的卷积运算，同时处理所有输入序列，通过堆叠较多的扩张卷积层、增大扩张系数以及增加卷积核尺寸，增加感受野尺寸的灵活度与算法适应性，使算法的漏洞检测效果与稳定性得到整体提升。

4 结论

1)以可变形卷积神经网络为基础，提出一种软件漏洞检测方法，当训练叠加至13期后，网络的过拟合现象开始突显，准确率、召回率以及误报率指标数据均逐渐上升，可以保证算法的可扩展性。

2)训练期数达到15轮后，8层网络的测试集损失、准确率、召回率以及误报率指标明显更具优越性，以满足行业安全的迫切需求。

3)在今后的研究工作中，应探索出一种介于中间且保留程序语义的固定规则表示方法，使其不受编程语言与硬件平台的限制，保证输入数据的理想性；在检测算法中将不同的漏洞种类划分成一类异常组，为后续的漏洞修复处理提供有效的补充信息，引用生成对抗网络，实现漏洞修复；需尝试结合新型的技术与算法，进一步提升检测算法的精准度与智能化。