基于霍夫圆检测的标志物多图像特征定位方法

刘爱胤，熊根良，姚健康，乐文辉

(南昌大学机电工程学院，江西 南昌 330031)

1 引言

艾灸作为中医治疗中一种重要的治疗手段，在国人心中有很高的知名度。与西医治疗不同，艾灸主要是用于医疗保健和疾病防范方面，它具有强身健体的功效，而且副作用较小，能广泛适用于各种人群。在《中国制造2025》明确指出把生物医药及高性能医疗器械作为未来重点发展的十大领域之一，这对我国的医疗器械业无疑会产生深远影响。近年来，许多高校、研究机构纷纷投入了对艾灸自动寻穴的研究中，研发出了许多卓有成效的自动寻穴的方法和系统。其中属通过视觉技术和神经网络来实现自动寻穴的方法研究地较为普遍。还有一些研究是利用人体某方面的特性来实现的，如利用人体穴位低电阻特性[1，2]，利用人体穴位处与非穴位处对光的吸收、散射和反射程度不同的原理等方法[3][4]也能部分实现自动寻穴的要求，但由于目前对这些特性的基础性研究还不完善，因此这些寻穴方法还存在很大的局限性，无法实现推广使用。

利用神经网络来实现自动寻穴的方法[5]，更适合于寻找特定的几个穴位点，而且当要寻找的穴位点增加时其寻穴精度可能会相应地下降，因此不适用于较大范围地寻找穴位。还有一个缺陷就是，它需要大量的样本来训练神经网络，工作量大，当需要寻找之前没有训练过的穴位时，需要重新对神经网络进行训练，因此这种方法适应性较差。相比而言，通过视觉技术来实现自动寻穴的方法则更为成熟，也是最早被引入到中医腧穴领域的一种技术。本文就是基于视觉技术来实现艾灸自动寻穴。

2011年山东建筑大学提出一种基于归一化相关模板匹配的穴位定位与跟踪研究方法[6]，通过对贴在人体穴位上的人工标志进行模板匹配，实现了移动人体的实时穴位定位与跟踪。但这种方法需要将模板图像按一定的顺序在检测图像上滑移，每滑移一次就要进行一次相关性计算[7]，直到遍历完整张图像为止，因此计算量较大。而且其对图像的灰度线性变换较敏感，一旦进入信息贫乏的区域，误匹配率会大大提升[8]。本文提出一种基于霍夫圆和标志物形心获取穴位点位置信息的方法，这种方法能够在精确获取穴位点位置的条件下，有效减少标志物检测时的计算量，从而加快算法的执行速度，提高算法的实时性。

2 图像霍夫圆检测

2.1 标志物的选择

本方法为了实现穴位点的快速寻找需要在主要穴位点贴上标志物。标志物要能满足，其形状计算机易检测[9]、颜色与人体肤色差异较大。因此，选择蓝色圆形标签纸作为标志物。因为圆形能够很容易地通过霍夫圆变换识别出来，且圆有很好的自相似性即使标志物有一定程度的倾斜也能被较好地识别出来。

2.2 图像预处理及霍夫圆检测

为了提高霍夫圆检测的运算速度和准确率，需要对原图像进行预处理来去除不需要的信息和消除部分干扰。首先将原图像转化为灰度图像，降低图像的信息量便于后续图像处理，然后进行直方图均衡化、二值化等一系列的处理，使图像中物体边缘更为清晰明显，对处理后的图像提取轮廓从而使图像边缘信息更为精简[10]。最后，对轮廓图像进行霍夫圆检测，获取标志物的位置信息。

霍夫圆检测是将图像中每一个像素点视为潜在圆上的点，通过投票生成累加容器，设置一个累计权重来定位圆。在X-Y平面内，任意一圆可以用(x-a)2+(y-b)2=r2来表示，其中(a，b)为圆心，r为半径，可将其视为二元函数f(x，y)=r2。亦可以将其变换为a-b-r空间中的函数(a-x)2+(b-y)2-r2=0，此时x、y便是常数，可将其视为三元函数f(a，b，r)=0。此时X-Y平面中圆上一点便对应a-b-r空间内一条三维曲线；X-Y平面的圆上所有点对应的a-b-r空间内的所有曲线都相交于一点，此点便是X-Y平面上圆的圆心(a0，b0，r0)，此种检测圆位置的方法便是霍夫圆检测。累加容器就是通过统计a-b-r空间内相交曲线的累积数量，当其数量大于一定的阈值时就认为这些曲线对应的X-Y平面内的点构成一个圆。

2.3 微小轮廓过滤

由于原始轮廓图中往往存在许多微小轮廓，而这些微小轮廓对标志物的霍夫圆检测正确率会产生很大的影响[11][12]。因此，需要一个合适的轮廓阈值筛选。对轮廓图进行先膨胀后腐蚀处理，使较近邻的轮廓之间相互连接，部分微小轮廓得到消除。统计各轮廓的长度，计算均值，以此均值的加权值作为阈值对轮廓图进行处理从而消除微小轮廓。公式如下

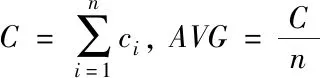
(1)

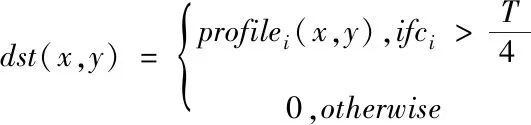
(2)

式中，ci为轮廓i的周长，n为轮廓个数，AVG为轮廓长度均值，profilei(x，y)为轮廓i的图像。微小轮廓滤除后的霍夫圆检测效果如下图1。

图1 霍夫圆检测

人体模特上贴有8个圆形标志物，图1(a)中检测出了43个霍夫圆，正确率为18.6%；图1(b)通过微小轮廓过滤后获得了12个霍夫圆，正确率为66.7%。轮廓过滤前后都没有出现标志物漏检的情况。

3 颜色检测

由于霍夫圆检测算法的稳定性不佳受环境因素影响较大，再加上人体生理凹陷、标志物不完全垂直于摄像头光轴等原因，图像中的标志物并不一定是标准的圆，会导致其检测效率低下，存在错检、漏检等情况。因此，在本算法中霍夫圆检测算法用于对图像中的圆进行初步检测，获取标志物的候选区域。为了最大可能地降低圆的漏检率，算法在不大幅增加计算量的前提下，调低了霍夫圆的检测条件，如降低圆心累加器阈值、扩大检测的圆半径范围，使得霍夫圆区域中包含所有的标志物。此时候选区域包含许多虚假霍夫圆，因此通过对候选区域进行颜色检测来将其消除[13]。

颜色检测需要将图像由RGB模型转为HSV模型[14]，此时任意颜色都是由色调、饱和度和亮度三个分量组成，而颜色变化的差异性主要是反映在色调上，颜色检测就是检测图像中指定色调范围内的颜色区域。标志物的颜色为蓝色，而蓝色对应的色调区域为75°～130°，对候选区域进行蓝色调检测便可消除虚假霍夫圆区域。颜色检测的流程图如图2:

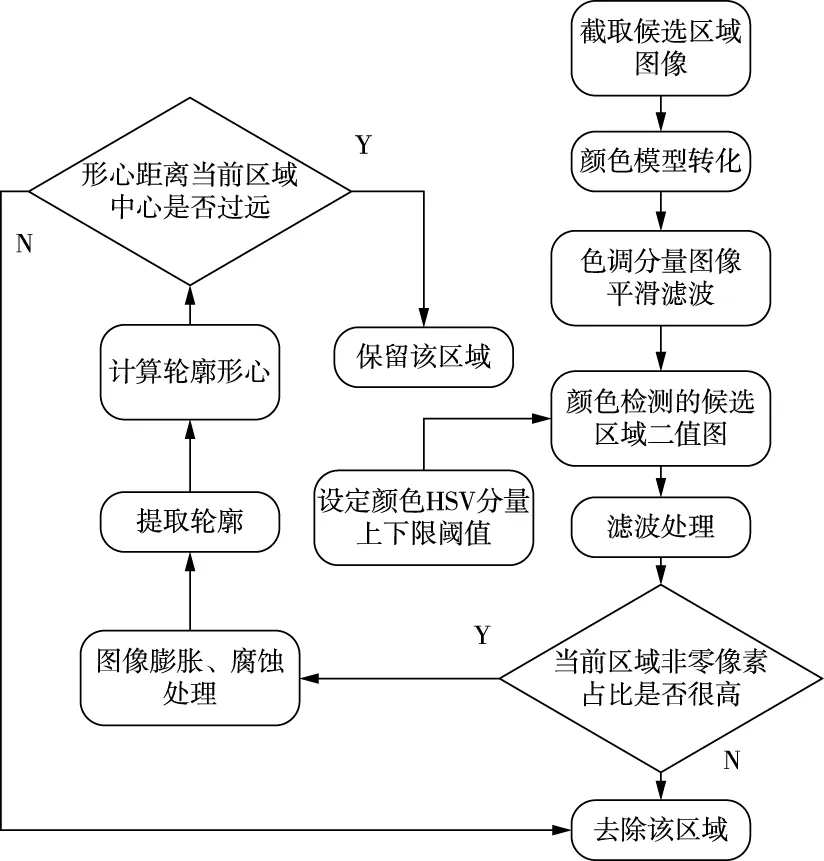
图2 颜色检测流程图

加入颜色检测后的结果如图3。

图3 候选区域颜色检测

标志物中有一个为红色，用于测试颜色检测的准确性，通过处理后图3中检测出了7个蓝色标志物，红色标志物、其它虚假霍夫圆均被滤除，正确率为100%。

4 标志物轮廓形心提取

颜色检测只是筛选出候选区域中的虚假霍夫圆区域，由于标志物在图像中不完全接近于圆的原因，霍夫圆的圆心并不一定与标志物中心重合。如图4所示，图中被红圈标出的标志物中的绿点为霍夫圆中心，其与标志物实际中心偏离，因此需要使用其它方法获得标志物的实际中心位置。

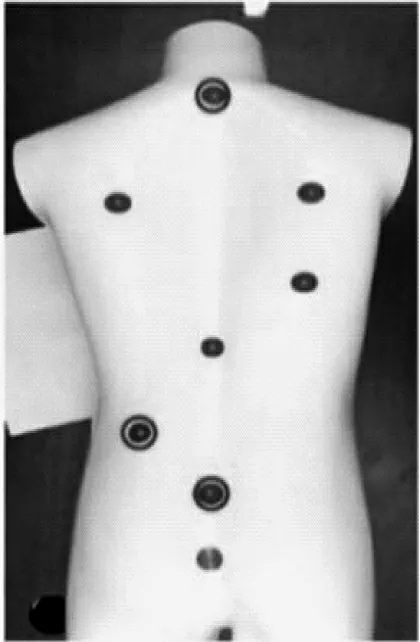
图4 霍夫圆中心位置

针对这种情况，为了准确地检测出标志物中心的位置，本文选择从标志物的形状特征入手。圆具有良好的自相似性和对称性，因此其即使在摄像头拍摄时由于标志物倾斜、标志物不完全垂直于光轴等原因导致图像中标志物变形，其形状也是趋于椭圆，而椭圆中心与标志物的中心还是重合的。受此启发，本算法提出一种基于轮廓形心的位置检测方法，实现对标志物中心位置坐标的精确定位。

轮廓的形心是由图像的几何矩mpq计算而来。设图像的像素尺寸为M*N，f(i，j)为(i，j)位置处图像的像素值，有如下公式

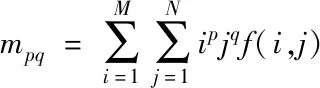
(3)

对于轮廓图像属于二值图，f(i，j)非零即1。m10便是图像关于x轴的一阶矩，m01为图像关于y轴的一阶矩，m00则是图像的原点矩。形心(px，py)的计算公式如下

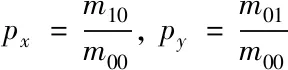
(4)

图5和表1所示，轮廓形心检测最大误差在1个像素内，而霍夫圆检测平均误差就达到了2.1个像素。因此，该方法获取的标志物位置比霍夫圆检测更为精准。

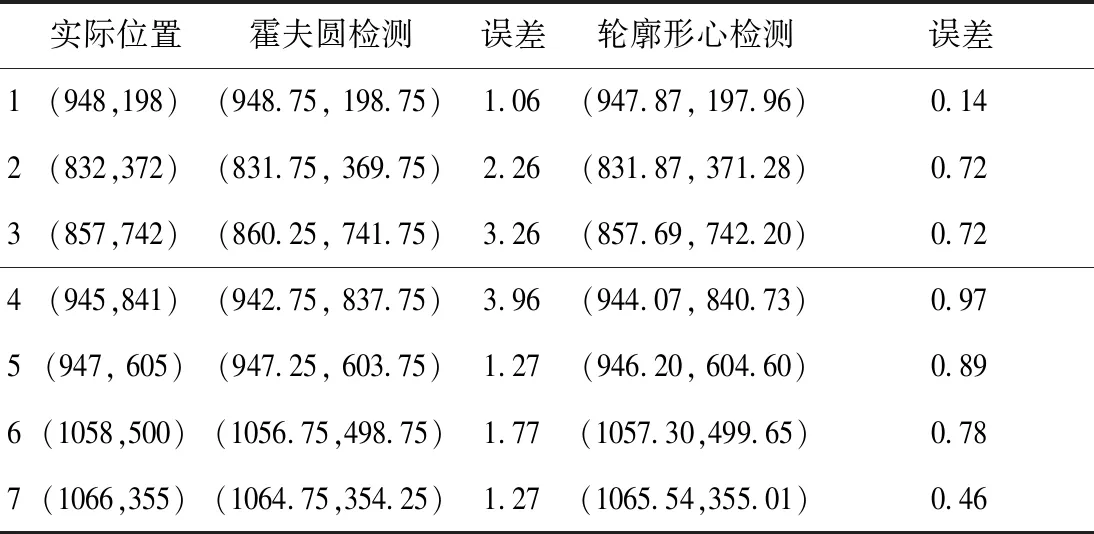
表1 不同方法获取标志物位置结果(单位：pixel)

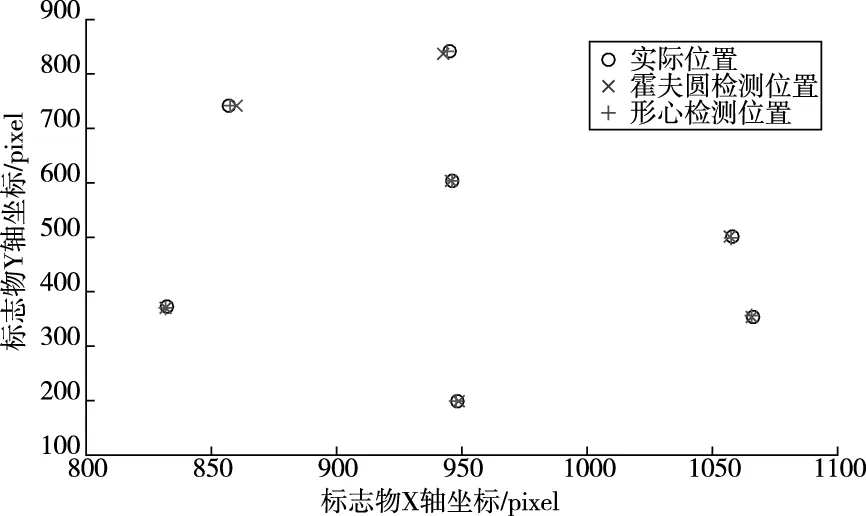
图5 不同检测方法获取标志物中心的图像坐标位置

5 标志物三维坐标获取

前面获取的标志物位置是基于图像像素坐标系，但在许多情况下空间三维坐标更为有用，其可用于控制执行机构。获取空间三维坐标还需要得到目标位置的高度信息，而单靠一个彩色摄像头较难实现高度的获取，因此本文利用深度摄像头获取高度信息，再采用坐标映射的方法实现彩色图像与深度图像的匹配，进而得到目标点的空间三维坐标。

深度图像匹配的目的就是将深度图像的图像坐标系转换到彩色图像的图像坐标系之下。设彩色摄像头对应的图像坐标和相机坐标分别为(uC，vC)、(xC，yC，zC)，深度摄像头对应的图像坐标和相机坐标分别为(uD，vD)、(xD，yD，zD)。此时存在如下公式：

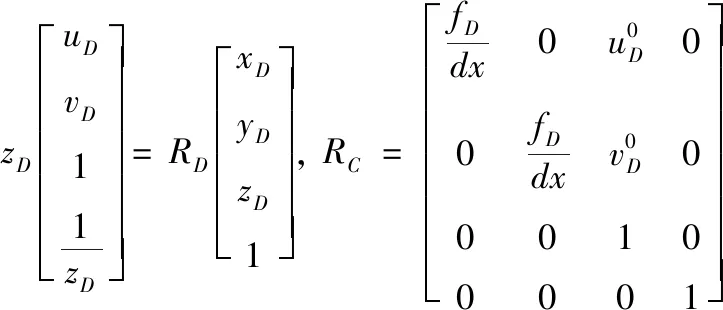
(5)

其中、RD分别为彩色图像和深度图像的内参矩阵。将两相机进行联合标定可获得两相机坐标系之间的外参矩阵M，M是由平移向量和旋转矩阵组成的4*4矩阵[15]。此时彩色相机坐标系与深度相机坐标系存在如下关系

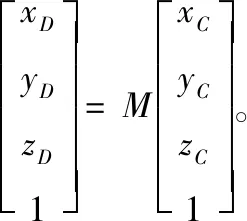
(6)

将上述方程联立求解可得彩色图像坐标与深度图像坐标的关系方程如下

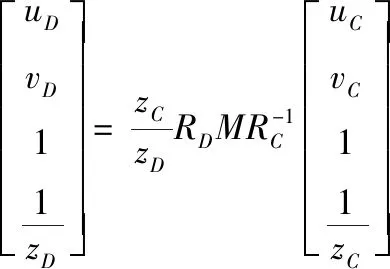
(7)

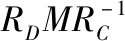
接下来就是将图像坐标转为三维空间坐标，如以下示意图空间坐标系以深度摄像头的中心点位置为原点，原点以左为X正半轴，原点以上为Y正半轴，原点向外为Z正半轴。

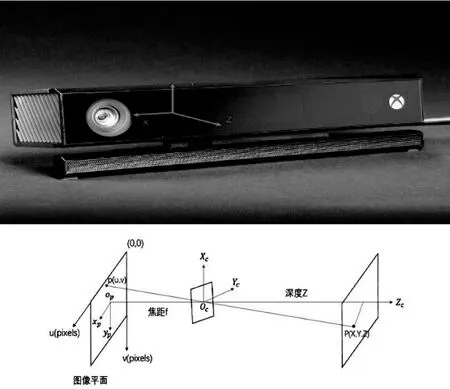
图6 相机坐标系及小孔成像模型

深度图像的像素值即是该点的深度，根据小孔成像模型和相似三角形原理可得：

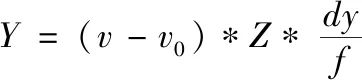
(8)

其中(u0，v0)为光心在图像平面上的坐标，dx、dy分别为每个像素在x轴、y轴方向的物理尺寸。由此获得目标点在相机三维坐标系下的坐标(X，Y，Z)。

如图7检测标定纸中黑白色块角点坐标，标定纸的右上角与光心重合，标定纸两边缘分别与相机坐标系x、y轴平行，摄像头到标定纸的垂直距离为103cm。实际位置和检测位置如表2。

图7 获取相机三维空间坐标

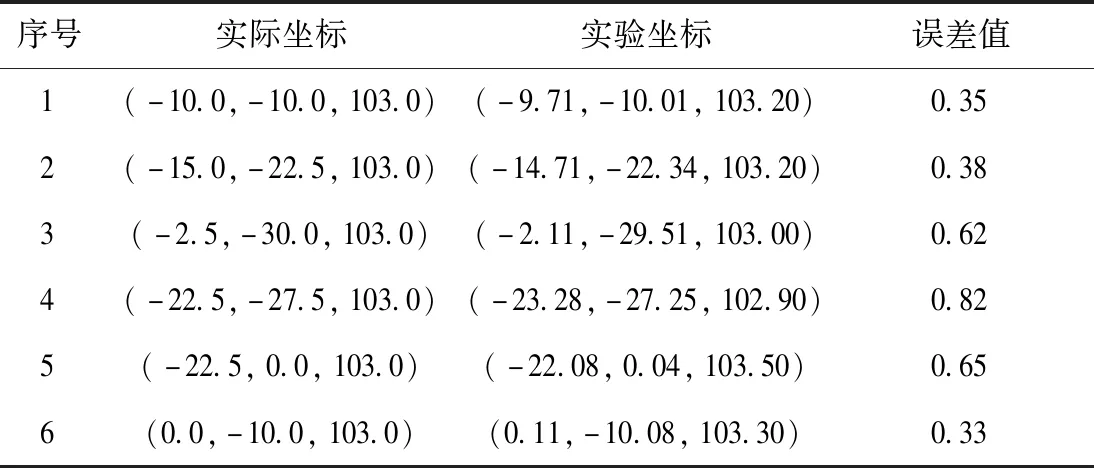
表2 相机空间三维坐标(单位：cm)

6 结论

本文设计了一种基于轮廓形心的的标志物目标位置检测的方法，该方法以霍夫圆检测获取标志物的候选区域，通过颜色检测对候选区域筛选，再计算轮廓形心获取标志物的精确位置，最后结合深度图像将目标点位置由图像坐标转换为相机空间三维坐标。该方法不仅克服了霍夫圆对标志物检测时不稳定的问题，而且在标志物存在变形的情况下实现了位置的精确定位，其精度能够在一个像素内，同时也实现了三维信息获取，具有位置获取精度高、实用性较好的特点。