基于SMPL模型的人体姿态估计

李 健，杨镖镖，张皓若

(陕西科技大学电子信息与人工智能学院，陕西 西安 710021)

1 引言

三维人体建模一直以来都是三维重建研究领域一个比较富有挑战性且比较重要的部分，其本质在于将现实世界中的人体以三维数字化的方式在计算机中存储并表示。高质量的人体三维模型在数字媒体创作、人体测量、虚拟试衣、游戏、三维动画、虚拟现实等领域有着广阔的应用前景。目前主流的三维人体建模方法主要分为以下三种：三维建模软件建模，即利用3D Max、Sketch up、Maya等基于计算机图形学原理开发的三维建模软件来生成人体三维模型；大型3D激光扫描仪建模，即通过Artec、RIEGL VZ-1000 等大型扫描设备对物体表面投射激光点阵，不断扫描并获取其三维信息；基于计算机视觉的三维人体建模，即使用普通RGB相机或深度相机来进行人体建模。基于计算机视觉人体的三维建模可以根据两个标准进行分类：一是基于模型先验，二是自由形式。基于模型先验的方法是利用参数化的人体模型来进行人体姿势和形状的估计[1]。随着人体二维关键点检测的进步，从单个图像直接对主要关节和粗略3D姿势进行3D估计方面也取得了进展[2-3]。2016年，Bogo F等人提出利用多个人体先验从检测到的14个二维关键点恢复线性模型参数[4]。然而，人体具有高度的复杂性和灵活性，从二维图像中恢复三维人体姿势和形态仍然具有很大的挑战。利用卷积神经网络(Convolutional Neural Networks，CNN)来回归参数模型可以一定程度上解决这一问题。2018年，Kanazawa A 等人提出利用基于回归的人体网格重构(Hot Module Replacement，HMR)算法[5]恢复人体姿态，但是其在自然图像中的表现仍然有待提高。随后，Alldieck T等人提出一种利用单目视频结合人体线性模型进行人体动态重建的方法，该方法可以将人体线性模型投影到人体轮廓当中，但是需要特定动作配合[6]。基于模型先验的方法可以适应更复杂的人体姿态，只需要少量的数据就可以获得粗略的模型，虽然模型缺乏准确性，但效率更高，也更简便。因此，基于模型先验的方法更适用于精度较低但效率较高的环境下。在基于自由形式的方法下，2016年Innmann M提出实时重建非刚性体[7]，然而需要输入高质量的多视图，这就限制了实际应用时的使用环境。2017年，Zhu H等人提出利用RGB视频对室外环境中穿着衣服的人体进行重建[8]，但是该方法要求人体长时间静止不动，使用范围受限。综上，现阶段基于自由形式的人体建模的方法的研究，对采集设备或者人体姿态要求较为苛刻，且模型内部没有装配动画骨架。因此，本文采用基于模型先验的人体建模方法。

2015年马普所提出了由姿态与体型参数驱动的蒙皮多人线性模型[9](Skinned Multi-Person Linear model，SMPL)，2018年Cheng Z Q等人[10]曾比较了Dyna[11]，SMPL和RealtimeSCAPE[12]几个典型的参数人体模型，得出SMPL模型在速度和准确性方面都比其它模型具有更好的表现，同时SMPL模型与现有的渲染引擎兼容。考虑到设备的便捷配置，本文仅使用单一设备。基于以上分析，本文使用单个Kinect相机和SMPL模型来进行人体三维数字化建模。

目前基于人体形变模型的姿态估计工作大多集中于单帧静态图像，由于单一视角的二维图像会丢失三维上的信息，在映射到三维姿态的时候，会产生一些不真实的姿态。为了解决上述问题，本文提出利用Kinect相机得到的人体三维骨架，拟合到SMPL模型上，弥补了二维图像映射到三维姿态时的缺失信息，从而提高了人体重建模型的准确度。

2 相关工作

2.1 SMPL人体模型

SMPL模型是一种参数化人体模型，该模型可以通过参数的改变进行任意的人体建模和动画驱动。其输入是10个体型参数(β，包含人的高矮胖瘦和头身比)和72个姿态参数(θ，包含24个关节相对角度)。将模型形状参数β和动作参数θ作用于基础模板Tμ进行动作变形，得到重构出的模型M(β，θ)以及模型的网格顶点位置T(β，θ)[9]。

M(β，θ)=W(T(β，θ)，J(β)，θ，ω)

(1)

T(β，θ)=Tμ+Bs(β)+Bp(θ)

(2)

其中W是一个混合蒙皮线性方程，其包含：

1)将β体型参数对应到骨骼关节的函数J(β)。

2)将θ姿态参数映射到模型对应点的变形函数Bp(θ)。

3)将β形状参数映射到模型对应点的变形函数Bs(β)。

4)各个关节的混合权重ω。

2.2 HMR算法

HMR算法是一个端到端的从二维人体图像恢复出三维人体模型的算法框架，算法网络框架如图1所示。

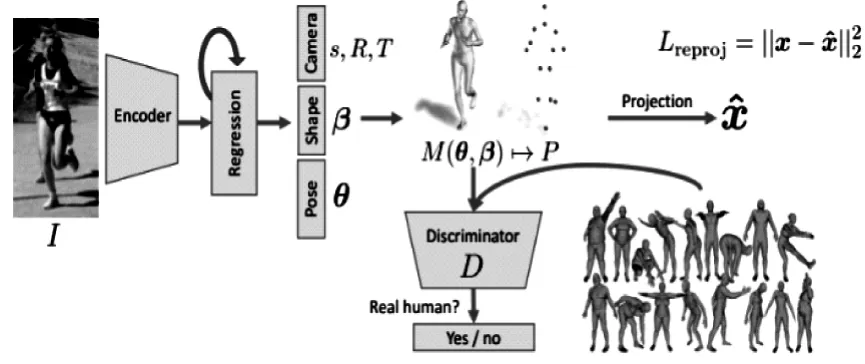
图1 HMR算法网络架构

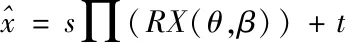
(3)

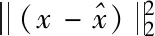
(4)

通过HMR算法估计的人体模型如图2所示。从图2中可以看出，算法在细节处(图2中圆圈所示)仍然存在一定误差。

图2 HMR算法结果

3 算法总体设计

基于SMPL模型的人体姿态估计中最主要的问题是如何将标准模板与真实数据进行非刚体配准，实质上就是为标准模板寻找合适的体型参数β和姿态参数θ，从而使β和θ所描述的人体模型与输入的真实数据实现最优配准。本文设计了一种基于SMPL模型的人体姿态与形状估计的方法，具有准确、快速的特点，能够在较短时间内生成一组完整的三维人体模型。该模型能够准确描述人体的真实姿势与形状，重建流程如图3所示。首先，具有任意姿势的用户站在Kinect传感器前，通过Kinect获取人体骨骼点信息，利用HMR算法从单张图片得到SMPL模型。然后利用迭代最近点(Iterative Closest Point，ICP)算法将SMPL模型的关节点和Kinect骨架点转换到同一坐标系下进行配准。接下来通过建立目标函数，迭代地将SMPL模型拟合到运动骨骼点上，得到优化后的模型。最后，利用摄像机标定获得的相机内、外参数将模型投影到相应的彩色图像上，得到近似于人体姿态的模型。

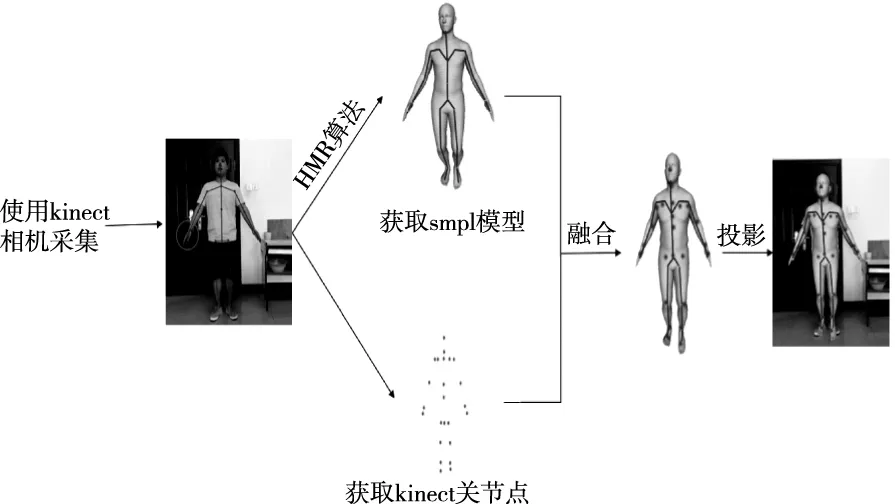
图3 重建流程

3.1 θ的整体刚性变换

姿态参数θ表示相对关节之间旋转的轴角，J(β)为根据人体形状参数β预测3D骨骼关节位置的函数[9]。然而通过J(β)得到的三维关节点只代表当前坐标系下所在位置，为了得到统一坐标系下SMPL的各个关节信息，需要进行全局刚性变换。对于关节i，将3D关节表示为Rθ(J(β)i)，其中Rθ代表由姿态θ引起的整体刚性变换[9]。本节将介绍如何进行这一变换。

罗德里格斯公式(Rodriguez formula)是计算机视觉中的一大经典公式，经常用于描述相机位姿的过程中。公式如下所示

R=I+sin(θ)K+(1-cos(θ))K2

(5)

I是单位向量，K代表旋转轴向量，θ是旋转角度，R代表旋转矩阵。通过使用罗德里格斯公式将每两个关节的轴角转换为局部旋转矩阵。当得到两个相对关节之间的局部旋转及其位置时，然后可以使用坐标的传递性来计算全局旋转变换和平移变换。

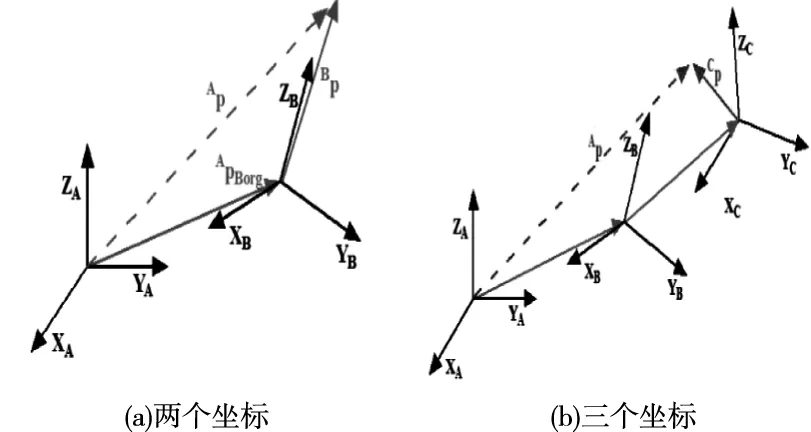
图4 同一点的坐标变换

如图4(a)所示，AP是坐标A中某一点的位置，BP是坐标B中同一点的位置，APBorg等于向量AP-BP，通过如下变换可以得到AP

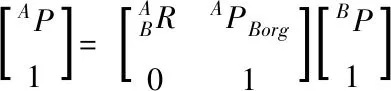
(6)

在图4(b)中，可以通过使用等式(7)将坐标系C中的CP转换成BP，并通过等式(8)将CP转换成坐标系A中的AP

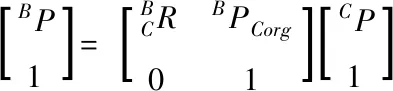
(7)

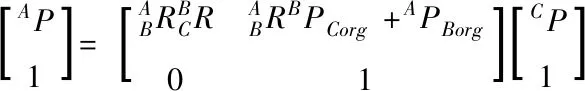
(8)

通过上述变换，可以将不同坐标系下的SMPL各个关节统一到同一坐标系下，最终可以得到SMPL的完整骨架信息，如图5所示。

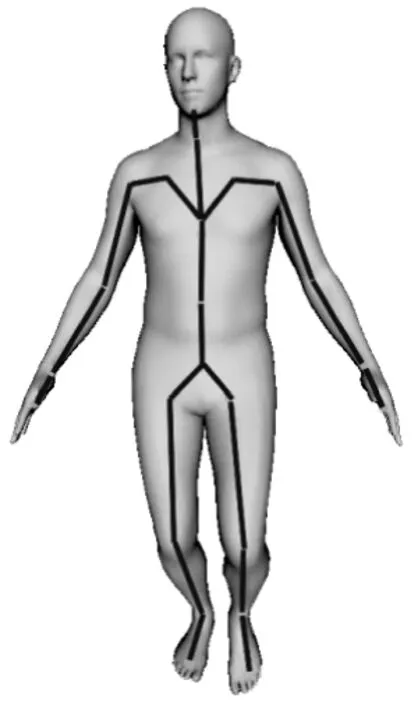
图5 3D骨架

3.2 将Kinect坐标转换为SMPL

由于SMPL三维关节与Kinect关节所在坐标系不同，需要将Kinect关节与SMPL关节变换为同一坐标系下。ICP算法是一种基于对应点的计算出最优旋转和平移的算法，常用于对齐两个点集。在已知对应点的情况下，有如下解决方案。

找到最佳刚性变换有如下几个步骤：首先，找到Kinect坐标点集A和SMPL坐标点集B的质心；其次将两个数据集都带到原点，最后找到最佳旋转R和平移T。

将两个数据集移动到原点后，计算协方差矩阵H，H矩阵定义如下

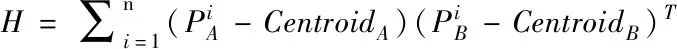
(9)

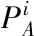
通过奇异值分解(SVD)计算得到最优旋转矩阵R[13]。

H=USVT

(10)

R=VUT

(11)

H是一个m×n的矩阵，U是m×m的矩阵，S是m×n的矩阵，V是n×n的矩阵。

通过式(12)得到平移向量T。

T=-R×CentroidA+CentroidB

(12)

最终通过式(13)将Kinect坐标转换到SMPL对应的坐标系上。

PSMPL=RPKinect+T

(13)

如图6(a)所示，显然，上方所在关节(Kinect关节)与下方关节(SMPL关节)之间的距离较远。由于躯体的刚性特质，将躯干关节作为对应点来求解旋转矩阵R和平移向量T，最终将两组点集统一到同一坐标系下，转换的结果如图6(b)示。

图6 使用ICP算法的比较

3.3 构造目标函数

利用HMR算法获得了人体的β，θ参数，然后通过θ得到SMPL的三维关节位置，接着将SMPL模型的姿态拟合到Kinect关节上。图7展示的是Kinect与SMPL骨骼点的比较。

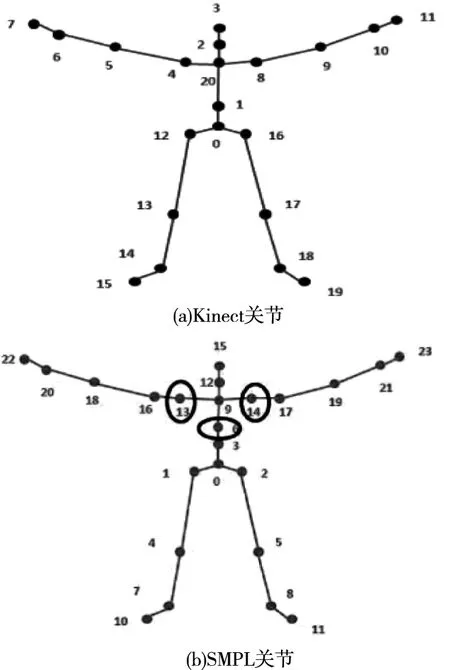
图7 Kinect与SMPL骨骼点的比较

首先，可以看到Kinect在图7(a)中有21个关节(实际上在Kinect中删除了手上的4个关节，因为不需要这些)，而SMPL模型在图7(b)中有24个关节，然而它们的关节并非一对一的。所以需要将Kinect的关节映射到SMPL模型上。例如，Kinect关节的索引12映射到SMPL关节的索引1。SMPL中有3个关节是分别索引6、13、14，而Kinect中没有对应的索引，所以需要计算它们周围点的平均值来求解它们的值。

此时需要建立一个目标函数来表示对应关节点的差异，并且尽可能最小化目标函数。目标函数公式如式(14)所示。

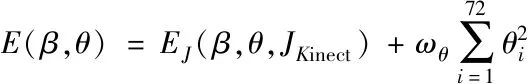
(14)

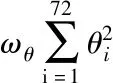
(15)

文献[5]使用的能量函数E(β，θ，J2D)，仅利用二维骨架的约束进行优化求解，不能精确的求解人体的真实姿态。本节提出的能量函数EJ(β，θ，JKinect)建立在Kinect三维骨架信息的基础上，通过求解对应关节点的最小欧式距离，得到相应的姿态参数。其中Joint代表对应的关节点个数24，wJ表示关节对应的权重，Rθ(J(β)i)代表θ全局刚性变换后得到的三维关节[9]，J(Kinect，i)表示对应的Kinect关节坐标。

在具体的实验过程中，利用Kinect相机获得三维骨骼点，通过SMPL模型得到三维关节点，在同一坐标系下，构造关节误差的目标函数，利用基于梯度的Dogleg法[14]最小化目标函数，得到相应的体型参数β和姿势参数θ。然后输入到SMPL得到完整的三维人体模型，并将得到的人体模型投影到彩色图像上。

4 实验结果及分析

4.1 实验环境

利用本文算法可以对自由移动的人体进行姿态估计。实验中将Kinect相机固定，人在Kinect相机前做任意动作，就可以得到与人体动作相似的人体模型。本实验以Kinect采取的六帧数据为例，详细分析本文算法在实验中的具体步骤，并与HMR算法和文献[6]算法进行比较。实验环境如下：

1)电脑配置：Intel Core i5-8300H CPU/16G，NVIDIA GeForce GTX1060Ti显卡/GPU 加速；

2)数据来源：Kinect相机。

3)算法实现：Chumpy、Opendr渲染库/Python语言。

4.2 实验结果

HMR算法是通过单张图片恢复人体模型，而文献[6]算法是利用彩色图的轮廓信息优化SMPL模型，选取这两种算法与本文算法进行对比。实验结果如图8所示，其中图8(a)为深度相机采取的彩色图，图8(b)为深度相机采集的3D关节图，图8(c)为本文算法重建出的模型投影图，图8(d)为HMR算法的模型投影图，图8(e)为文献[6]算法的模型投影图。

图8 姿态估计算法对比

HMR算法不仅体形上与彩色图人体差距较大，而且在一些细微的姿势上，不能很好的与人体重合，如手臂、脚部、膝盖等；而文献6算法仅限在A型姿势估计时效果较好，但与本文算法相比，仍然有所不如，且复杂姿态下得到的结果与真实人体姿态相比差异较大。如图8(c)所示，图中黄色圆点代表Kinect关节，绿色圆点代表SMPL关节点，蓝色代表SMPL骨架，可以看出，SMPL骨架能较好的拟合到Kinect关节上，从而使得得到的人体模型更接近真实人体。相比其它两个算法，本文方法能够将三维模型较为准确的投影到彩色图像上，有效估计了人体的三维姿态。

为了验证本文方法的有效性，选取豪斯多夫(HuasdOrff)距离来计算模型关节与Kinect关节点之间的均方根(Root Mean Square，RMS)误差。与欧式距离不同，Huasdorff距离定义为两组点集之间的距离，是描述两组点集之间相似程度的一种量度。

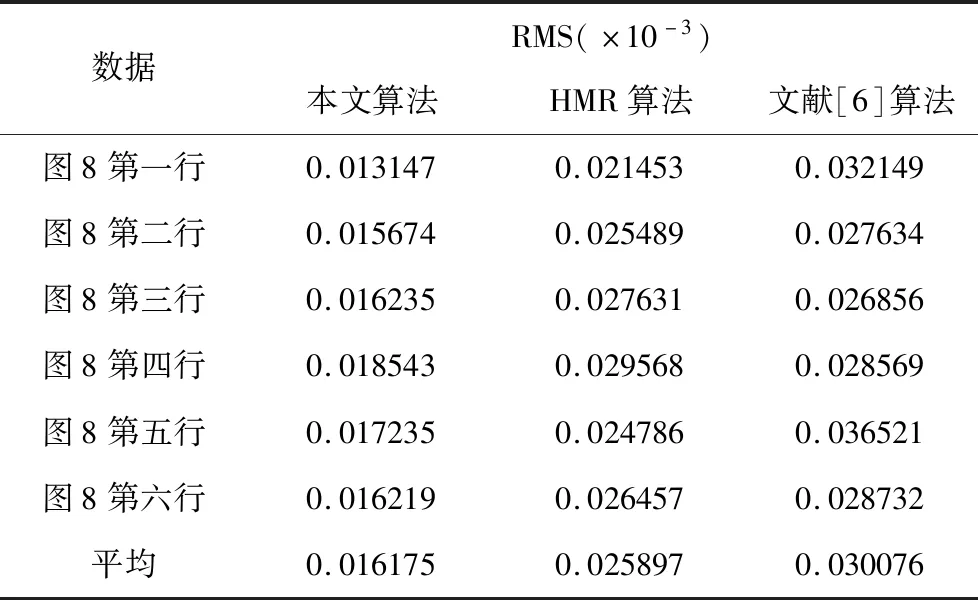
表1 定量分析表

对比结果如表1所示。从表1的对比结果分析，无论是踢腿、半蹲还是举手等动作，本文方

法在误差表现上都优于其它两种方法。综上所述，本文算法能够有效利用Kinect三维关节点的约束对人体模型参数进行求解，并且得到相对优于HMR和文献[6]算法的结果。

5 结论

本文通过总结和分析基于模型的人体姿态估计算法的研究现状，发现了目前算法存在精度有限、信息缺失等问题。针对这些问题，本文提出将Kinect三维关节点拟合到SMPL模型上，来恢复更真实的人体网格模型的方法。

该算法具有以下三个优势。一，采用Kinect相机采集数据，快速便捷；二，通过Kinect得到的人体三维信息，弥补了由二维图像映射到三维姿态时的缺失信息，减少了姿态估计时的误差；三，相较于从彩色图像拟合人体模型的方法，本文利用更能反映人体真实姿态的三维人体骨架，提取的特征维度更高，能够更详细的描述目标信息。实验结果表明本文方法较HMR方法在RMS误差上平均减小了37.5%，较文献[6]方法平均减小了46.2%，综上，本文算法通过人体三维信息的补足和约束，提高了姿态估计的精度，得到了更真实的人体模型。

文中使用的 SMPL 模型是不包含脸部与手部的模型，在后续的工作当中，可以考虑使用最新的人体形变模型[15]，来进行更为全面(包含脸、手等多部位)的人体姿态建模，并结合光照和人体纹理等信息来构建出更为逼真的人体模型。