一种改进A*算法在无人船路径规划中的应用
2021-11-17袁宇浩
陈 新,袁宇浩,饶 丹
(南京工业大学电气工程与控制科学学院,江苏南京 211816)
1 引言
水面无人船,可以简称为(USV),其主要用于军事作战、海上监视巡航、海洋环境等领域。作为监测海洋环境、维护海洋权益的现代化装备,具有广阔的应用前景[1]。当前,美国、以色列等国在这方面的研究已经取得了一定成果,结合美国军方出版的“美国国防部无人系统综合路线图”和美国海军出版的“海军无人船总体计划”[2]相结合,USV研究所涉及的关键技术主要包括:自动路径生成与路径规划技术、自主决策与避碰技术、水面目标检测与目标自动识别技术以及通信技术[3]。
自动路径生成和路径规划技术主要研究USV全局和局部路径规划,全局路径规划基于完全信息,而局部路径规划基于传感器获取的信息[4]。当前路径规划的方法主要有A*算法、人工势场法、遗传算法和蚁群算法等;在局部路径规划方面最近也产生了一些新的方法,例如强化学习法、D*算法等[5]。目前,国内外相关学者都在对USV的全局路径规划方法进行深入研究,并已取得一定的成果。卢艳爽采用A*算法结合海事规则实现全局路径规划[6];饶森应用激活值和遗传算法,利用分层思想完成了全局路径规划[7];庄家园提出了一种基于电子海图的距离寻优Dijkstra算法,该算法可以减少规划时间,提高规划精度并产生安全合理的路径[8]。Hanguen Kim在考虑海洋环境和USV最大曲率的地图中设计了基于A*算法的3-D曲率路径规划算法[9];Song C.H在栅格环境模型中应用改进的蚁群算法完成USV的全局路径规划,验证算法的有效性[10]。
电子海图是为适应航海需要而绘制的地理信息和海事信息的数字地图[11]。如果能够充分运用这些信息自动获取水面无人艇到目的地的所有可航区域和不可航区域,则将会为水面无人艇设计计划航线提供重要参考。本文在完成对电子海图数据读取、建立环境模型的基础上,提出了一种基于距离信息和角度变量的改进A*算法,将其运用在水面无人船全局路径规划。
2 海洋环境模型的建立
雷达、相机和其它传感器无法提供完全的海洋环境信息,而USV却需要在广阔的海域中航行,因此拥有可以提供详细而准确的全局海洋环境信息的S-57电子海图是必不可少的。对电子海图中的海洋环境地理信息进行统一描述,并采用栅格法进行环境建模。栅格化的电子海图一致性表述是提高路径搜索算法效率的基础。
2.1 电子海图数据提取
电子海图主要由海域要素组成,具体表现为海底地形、航行障碍、导航标志、港口设施等要素[11]。S-57电子海图是一种便于进行数据交换和传输的髙度压缩的数据格式,其标准封装格式为ISO/IEC8211国际标准,海图文件包括数据集的描述信息、特征记录和空间记录[12]。将此电子海图应用到USV全局路径规划中,需先按其对数据解析、提取和存储;因此本文采用ISO8211开源库,根据S-57电子海图的文件包结构对所有电子海图数据进行解析。S-57电子海图解析和存储的流程如图1所示。
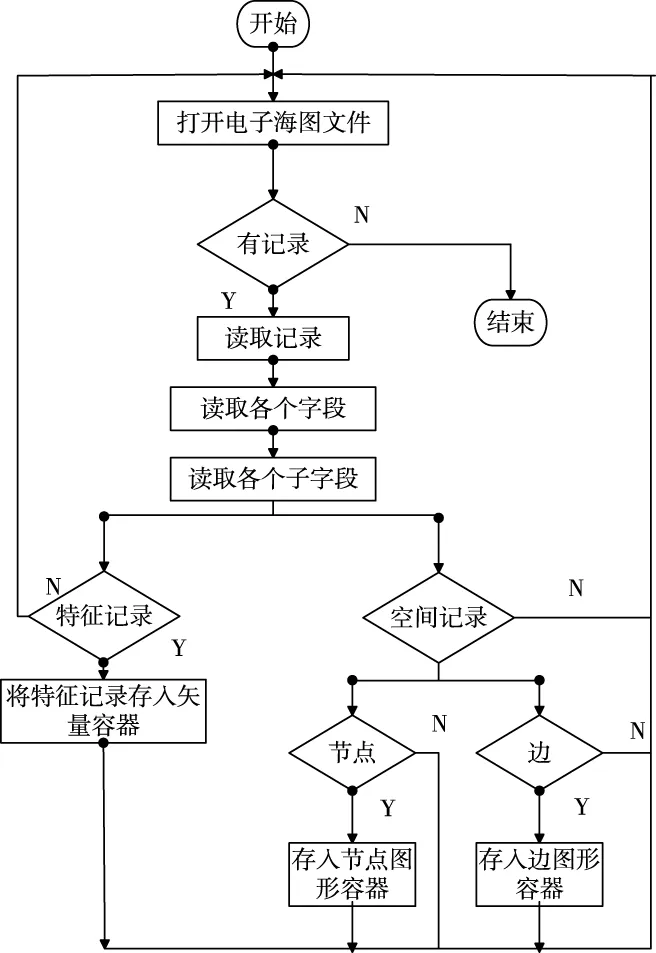
图1 S-57电子海图解析和存储流程图
读取电子海图文件中的每条记录,特征记录用矢量容器存储,空间记录用图形容器存放。将包含陆地和岛屿等障碍物的海洋环境空间描述成USV能识别的海洋环境信息。
2.2 环境模型的建立
USV环境模型的建立可以简化为:USV在海平面有限的区域内移动,区域中存在着有限数量的静态障碍物,障碍物的形状和分布位置是不确定的。环境建模方法一般分为栅格法、几何法和拓扑法3类。由于采用栅格法建立环境模型简单有效,且便于维护和修改,因此本文采用栅格法来表示环境模型。
环境模型的栅格化是通过将区域转化为一个矩形图,用网格方法将矩形划分为多个等尺寸网格单元,将阴影部分填充区作为障碍物区域。本文根据依次提取的信息判断网格中是否存在陆地和岛屿等障碍,以便在网格单元中建立可通航区和不可航行区。
原始环境模型和可航行判断后的环境模型如图2(a)、(b)所示,其中阴影部分表明是不可航行区域。
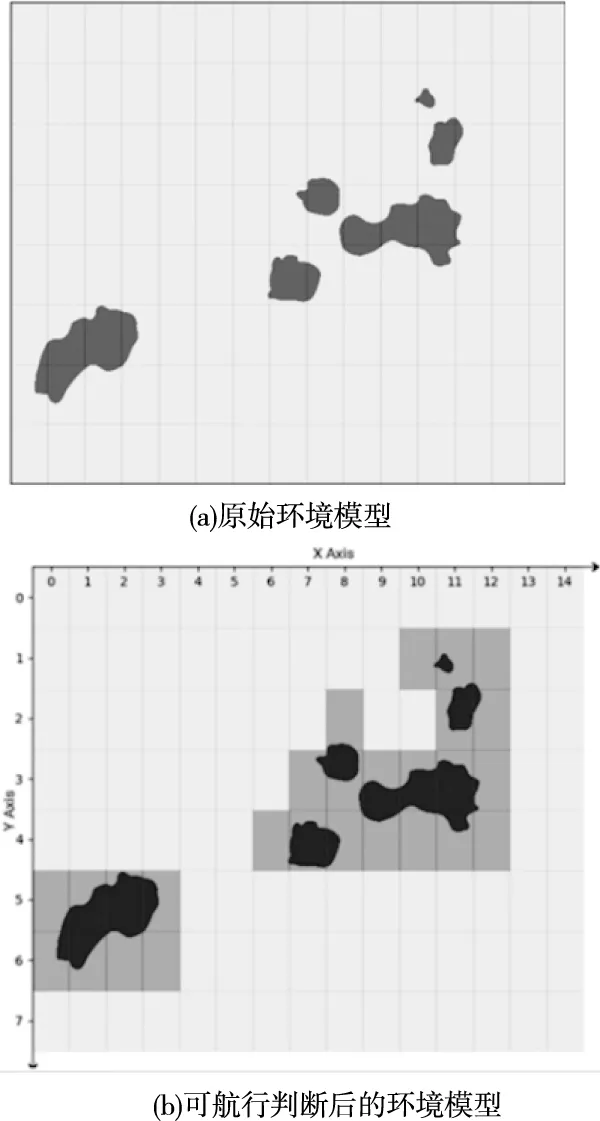
图2 环境模型
USV的仿真环境经栅格化后成为栅格地图,栅格法的一致性和规范性使环境空间变得简单有效,从而将全局路径规划问题转化为在栅格网中寻找2个栅格节点之间的最优路径问题。
3 改进A*算法的描述与实现
3.1 传统A*搜索算法基本思想及缺点
在路径规划算法中,A*算法是一种经典的启发式搜索算法。其基本思想是使用预设的代价函数来计算当前节点可能到达的每个相邻子节点的值,并选择最小成本节点加入搜索空间并展开,以此类推,直到到达目标点为止[13]。A*算法综合考虑了起始点到当前节点的真实代价和当前节点到终点的估计代价,因此可以引导搜索方向。
其中代价计算方式如式(1)所示
f(n)=g(n)+h(n)
(1)
f(n)——经过当前节点n的全局评估代价值;g(n)——起始节点到当前节点n的真实代价值;h(n)——当前节点n到目标节点的代价估计。
在评价函数中,启发函数h(n)对A*算法起主要影响作用:h(n)估值越小,A*算法需要计算的节点就越多,此时的算法效率就会降低,逐步趋近Dijkstra算法;但如果h(n)估值很大,甚至远大于g(n),此时g(n)的作用便会失效,逐步趋于BFS算法,只追求速度无法获取合理路径。
传统A*算法虽然能够规划出一条全局路径,但是往往在特殊复杂环境下规划效率低,且路径线路不优,具体问题表现在:无人船航行的环境里存在着许多不规则形状的岛屿、礁石等障碍物,如果采用传统A*算法规划路径,USV会在各个拐点或者障碍物处容易出现线路抖动甚至卡死现象,降低了规划效率,增加了路径拐点数和航行总距离。
3.2 改进A*算法
在上一小节提到过启发函数h(n)对A*算法起主要影响作用,它表示的是当前节点C到目标节点的距离代价估计值。在传统A*算法中距离估计一般采用曼哈顿距离,以X、Y方向上的距离差的绝对值之和作为估计距离,h(n)函数如式(2)所示
h(n)=|Cx-Gx|+|Cy-Gy|
(2)
式中:C为当前计算节点,G为目标节点,x,y分别是节点对应的距离行列号。
在保证USV行进间与障碍物有一定安全距离的约束下,本文主要对A*算法的启发函数h(n)做出改进,以分区加权方式来表达距离信息,以向量叉积来表达角度信息,新的启发函数h(n)+如下式(3)所示
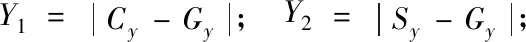
(3)
式中,S为起始节点,C为当前计算节点,G为目标节点,x,y分别是节点对应的距离行列号,p,q,w是权值。
权值p,q的设置使得h(n)可以根据节点C所处区域的不同进行调整,更好地引导搜索方向;变量w使得h(n)可根据节点向量间角度变化作出调整,诱导分布在起止点连线附近的节点趋近于S-G直线上。总而言之,本研究是根据节点C所处位置的不同调整启发函数h(n),获取更理想的h(n)值来引导路径搜索,权值选取的详细描述如下。
1)距离信息表示
常用的距离估算方式有曼哈顿距离、切比雪夫距离和欧几里得距离,三种距离估算方式具体含义和作用如表1所示:

表1 三种距离估算方式的含义和作用
因为欧几里得距离和切比雪夫距离在障碍复杂环境下与真实代价的偏差较大,所以本文选择在多障碍环境下距离估计更准的曼哈顿距离更为合适。
为避免路径行进中遇到节点代价相同而造成的路径不确定性和抖动现象,将坐标差加权后再求和。通过设置十组权值比{1∶9,2∶8,…,9∶1}进行路径搜索,最后确定权值比6∶10效率最高,即选取p=0.6,q=1。而分区加权是为了起到一定的方向引导作用。
分区加权对引导作用的体现如图3所示,以终点为坐标原点,以X=Y作为分割线,左下方区域中当前点到终点在X方向距离差大于在Y方向距离差,此时定义X1的权重为小系数,由于在选择计算点时优先选择代价小的节点,故将会引导搜索方向朝X1小的方向前进(箭头标识),同理分割线右上方的区域则会朝Y1小的方向前进(箭头标识)。分析起止线左偏的情况同样适用。
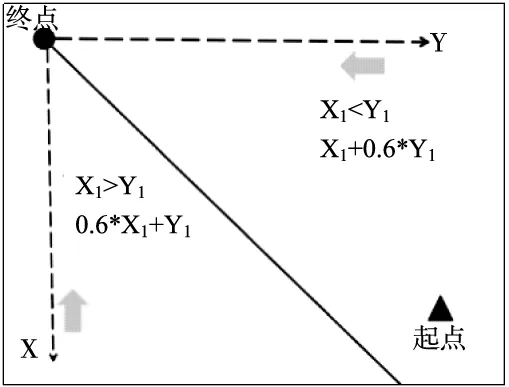
图3 距离函数几何意义分析
2)角度变量表示
有时规划出的航行成本最小的路径不止有一条,虽然最终结果只需要一条;或者规划出的航线不合理,因为分布在起始点S到目标点G连线附近的节点偏离起始点S和目标点G之间的直线LSG过多。为此,在启发函数中加入角度信息变量,来引导A*算法偏向拓展分布在起始点S到目标点G连线附近的节点。
在式(3)中加入的角度信息变量是两个向量的叉积结果的模。如图4所示,将起始点设置为S,目标点为G,当前节点为C,通过式(4)计算向量叉积得到S-G向量与C-G向量之间的角度θ
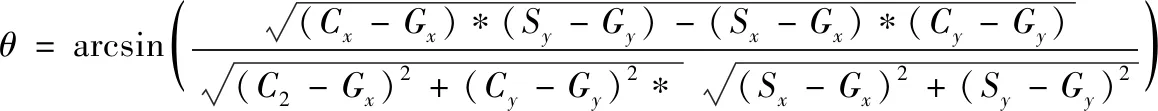
(4)
式中,C为当前计算节点,G为目标节点,x,y分别是节点对应的距离行列号。
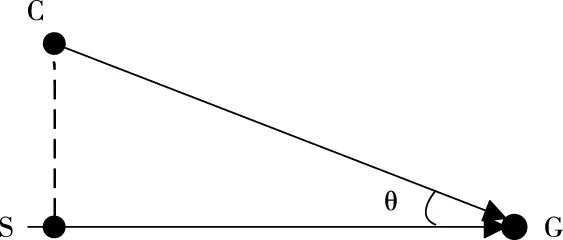
图4 角度函数几何意义分析
通常情况下起止点距离|SG|是常量,而|CS|是随着两向量夹角变化而变化的量,当两者平行的时候,|CS|达最小值,当两者垂直的时候,|CS|达最大值,它很好地以距离的形式反映了两者间的角度关系。因此,在启发函数中加入角度信息变量可诱导A*算法偏向拓展分布在起始点到目标点连线附近的节点。在本研究中将当前点C角度权重w表示为式(5)所示
w=3/(4-sin(θc))
(5)
3.3 路径优化
如果把规划出来的路径点连接起来作为水面无人艇的航行路径,折线会过多。路径中的多余节点指的是那些去掉以后不会影响路径的有效性和安全性的节点。出现的多余节点使得规划出来的路径有时会出现阶梯和锯齿状的线段。将规划的结果作为航行路径要经常改变航向,这样对水面无人艇的控制提出了很高的机动性要求。为此需要对规划的路径进行优化,以减少路径中不必要的路径点,增加路径的平滑度。
路径平滑的方法是遍历规划路径中的所有节点,当节点i和i+2之间的连接不存在障碍时,删除剩余节点i+1。继续上述的步骤直到i和j之间的连接线穿过障碍物为止,然后在节点i之后取出3个连续节点mj-1、mj和mj+1,继续这些步骤,直到已经遍历了整个路径中的所有节点。
4 仿真验证
为了验证所建环境模型和改进的A*算法的可行性和有效性,对上述算法进行了仿真。基于Map Objects开发的电子海图显示平台界面,路径规划仿真环境利用IDLE(Python3.6)开发,运行于PC机。基于电子海图的USV全局路径规划流程如图5所示。实验中实现的主要功能有:设置USV和电子海图参数;根据USV的参数信息获取并显示电子海图中障碍物的空间几何信息;完成海洋模型的建立,设置栅格大小,对电子海图进行栅格化;启动改进A*算法程序,完成全局路径规划。
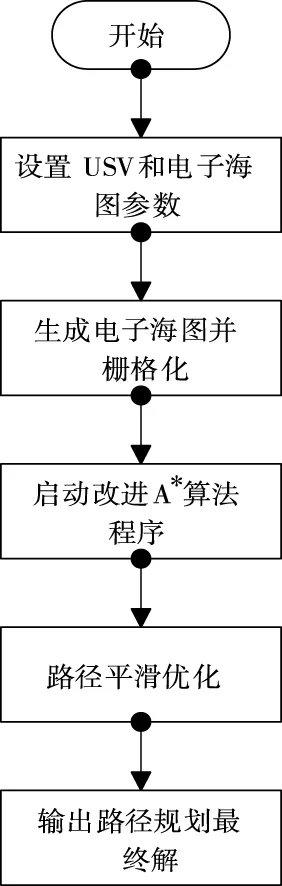
图5 全局路径规划流程图
选取中国某海域(区域坐标范围为东经112.50度至113.00度,北纬21.50度至21.98度)海图环境,在实验中,设置USV的起始位置均为(东经112.663度,北纬21.829度),终止位置均为(东经112.753度,北纬21.665度)给出仿真验证结果。
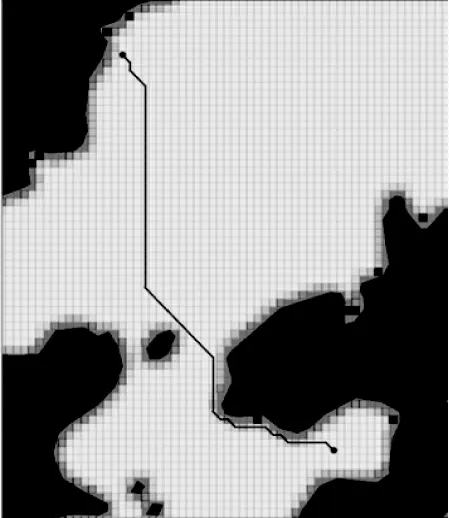
图6 传统A*算法路径规划图
如下图6所示是在栅格化电子海图环境模型下传统A*算法路径规划图,;图7所示为改进A*算法和传统A*算法路径规划效果对比图,实线为算法改进后的路径;从图中可以明显看出实线路径走向要比虚线路径好得多。图8所示为对改进算法路径平滑优化后的全局路径和没有平滑优化的路径对比效果图,其中线a表示平滑优化过的效果图,线b是表示没有平滑优化过的;从图中可以看出,经过平滑优化过的全局路径转折点更少,曲线更加平滑流畅。
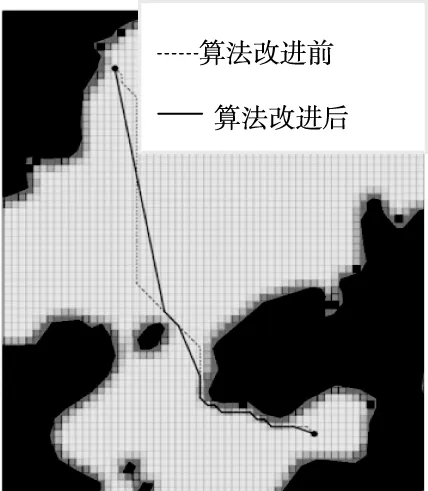
图7 改进A*算法和传统A*算法路径规划对比图
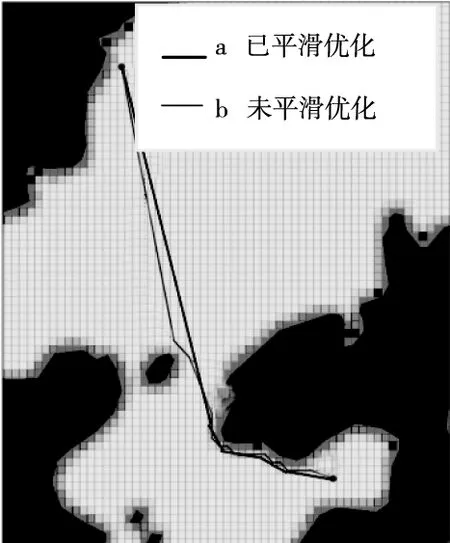
图8 路径平滑优化前后效果对比图
表2所示是仿真后的三种结果各个指标的对比图,在航行距离方面,使用传统A*算法的距离最远,而改进算法后USV的航行距离减少了0.58,在这基础上加入路径平滑优化后航行距离进一步减少了0.49,降低了USV的航行成本。与此对应的路径节点数也发生了改变,传统A*算法路径节点数有38个,而路径平滑后的改进后A*算法只有19个路径节点;节点数减少使得USV航行时转向次数减少,在保持安全距离的同时路径更加平滑,线路抖动甚至卡死现象大大改善。在规划计算时间方面,由于对启发函数加入了权值和变量信息,导致计算时间相较于未改进前有所增多。
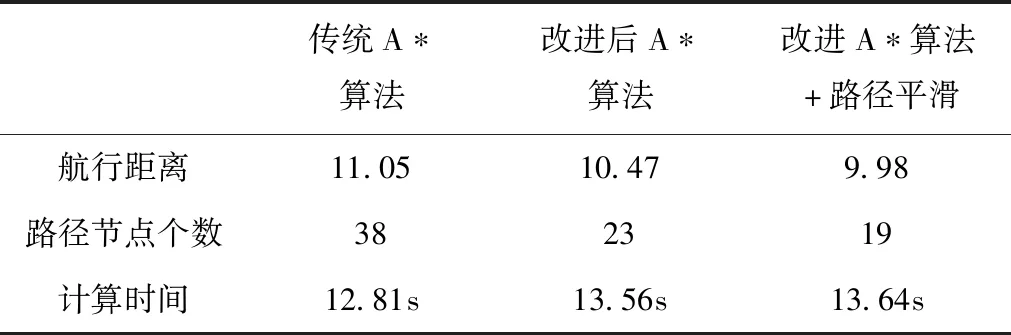
表2 仿真结果各指标对比表
5 结论
针对USV复杂的工作环境下,传统A*算法规划全局路径容易在各个拐点或者障碍物处出现线路抖动甚至卡死现象的缺点,本文基于栅格化后的S-57电子海图仿真环境模型,提出了一种对启发函数h(n)结合了分区距离信息和角度变量信息加权的改进A*算法并用于USV全局路径规划中;最后再使用路径曲线平滑法进一步优化。通过仿真实验验证得出该算法能准确地在给定海域内任意两个起止点之间生成无碰撞全局路径。相较于传统A*算法,改进A*算法虽然牺牲了规划计算时间效率,但是规划航行距离缩短,USV航行时转向次数减少,路径更加平滑,线路抖动甚至卡死现象大大改善。
