基于割点移除的社交网络重要节点评估与仿真

王 安，顾益军

(中国人民公安大学信息技术与网络安全学院，北京 102600)

1 引言

随着复杂网络科学的不断研究与发展，人们发现许多具备引用，共现关系的事物几乎都可以被转化成复杂网络。人类的社交关系的呈现出一定的组织结构，其构成的社交网络同样可以被转化成复杂网络的表示。为了对社交网络的人员进行有效地控制与管理，需要对社交网络中的节点与结构进行详细的分析。在社交网络中，一些节点在网络中处于关键的位置，如果这样的节点受到攻击不能发挥作用，就会导致整个网络的连通情况发生较大的变化，整个网络的功能也会受到较大的影响[1]。以社交通信网络为例，一些关键人物承担起重要的通信桥梁，对于这样的角色，所处的位置较为特殊，所扮演的角色较为关键，采取特定的打击便可以使整个网络崩溃。因此发掘出对于社交网络整体结构和功能起到关键作用的重要节点至关重要。

对于社交网络重要节点的评估，已有许多成熟的方法[2，3]，最为经典的方法是应用复杂网络中的中心性[4，5]，基于随机游走的PageRank[6]等方式从不同角度测定了各个节点的重要程度，进而对节点进行排序。

近年来国内外学者针对社交网络中节点重要性问题提出了一些新的改进方法。吕琳媛[7]等人在PageRank的基础上增加了背景节点，形成LeaderRank算法，将整个网络变成强连通网络，提升了算法的迭代速度与重要节点的传播性能。在LeaderRank的基础之上，顾亦然[8]等人引入节点间的相似度，以此来评估节点间的相互关系，进而得到节点的重要性表示。Hu[9]等人将社区划分与K-shell进行结合，有效的提升了K-shell算法在传播性能上的表现。然而以K-shell为代表的算法其分辨率都较差，很多节点会具有同样的重要程度。韩忠明[10]等人提出一种基于节点间的特殊三角型结构的LTC影响力度量模型，在SIR性能提高较为明显。上述方法或是基于已有算法进行改进，将原始算法加入新的特征，或是直接将复杂网络中节点间的特殊关系作为节点重要性排序的依据。而以TOPSIS[11]为代表的综合性评估方法，将多种指标进行了融合，考虑更加全面，但是与此同时也增加了算法的复杂度。

以上方法都关注了节点的不同特征，但上述算法大多都是从传播动力学模型进行综合评估，得到的重要节点在传播影响力指标上有一定的效果。对于社交网络，一些节点对于网络的鲁棒性影响同样是重要的指标，依次移除这些节点后对网络结构和功能会有不同的影响。

本文从社交网络中一些节点在结构上具有的特殊性质出发，重点关注这些节点在对整个网络结构和功能上的影响，提出一种基于复杂网络割点移除的节点重要度评估方法APRRank(ArticulationPointRemovalRank)

2 割点以及Tarjan算法

2.1 复杂网络中的割点

定义1 割集：在一个无向图中，如果有一个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，图的连通分量增多，就称这个点集为割集。

定义2 割点：在一个割集中，若该割集仅有一个节点，则称该点为割点(Articulation Point)。

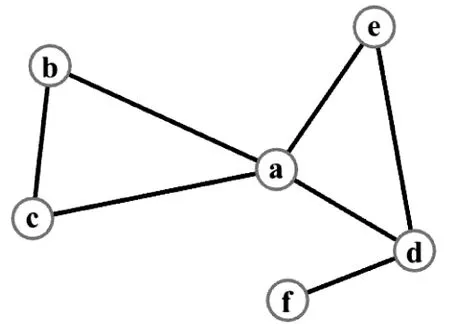
图1 割点示意图

如图1所示，在无向连通图G中，如果将节点a或者节点d及其所有的连边移除，该无向连通图G便不再连通，那么在该图中节点a和节点d就是割点。

2.2 利用Tarjan算法求取割点

求取割点有多种方法，其中最经典的便是Tarjan算法[12]。Tarjan算法是一种基于深度优先搜索(DFS)的，可以在线性时间内得到无向图割点的算法。在Tarjan算法中定义了两个数值：

定义3 DFS时间戳(DFN)：对每一个节点在深度优先搜索中被遍历时的顺序记作为节点的时间戳。记节点v的DFS时间戳为DFN[v]。

定义4回溯值(LOW)：一个节点或者它的子树通过反向边能到达的最小DFS时间戳。记节点v的回溯值为LOW[v]。

Tarjan算法在一次深度优先搜索过程中，得到所有节点的DFN和LOW值。利用以下规则判断节点v的是否为割点：

1)v为根节点时v的子树数量大于一颗。可以理解为，若移除该根节点，则会产生多颗子树，则图便不再联通。

2)v为非根节点，节点v存在一个子节点u使得节点v和节点u符合式(1)要求

DFN[v]≤LOW[u]

(1)

可以理解为从v的子节点u反向追溯，无法到达比 节点v更早被访问的节点。

图2 Tarjan算法求取割点过程示意图

Tarjan算法求取割点的过程如图2所示，以节点e为DFS的根节点遍历整个网络的所有节点。图中节点a为非根节点，它的子树上节点b的回溯值LOW[b]大于等于a的时间戳DFN[a]，所以节点a为割点，同理节点d也为割点。

3 基于割点移除的节点重要性方法

本文对社交网络重要节点的评估采用的是复杂网络节点重要性排序的方法。在诸如话单网络，朋友关系网络等社交网络中，通常需要得到一些重要的人物节点，这样的人物节点通常具有核心的作用。在复杂网络中最直观的解释是，一旦这样的节点失去相应的功能或者无法正常运转，会导致整个网络受到较大的损伤。

实际上，由于割点的定义就是去掉后图便不再连通，所以移除图中的割点便能很好的破坏网络的结构。

而在一个图中可能会有很多的割点，如何在这些割点中选择“最好”的割点便是一个关键问题。这里将“最好割点”定义为移除该割点后能使最大联通分量规模减小最多的节点。笔者发现，通常这样的节点具有较高的度中心性。度中心性的计算方式如式(2)所示

(2)

实际上在这里可以将度中心性替换为PageRank，PageRank迭代计算方法如式(3)所示

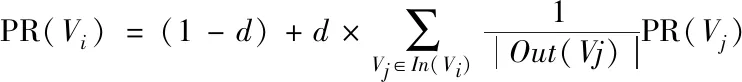
(3)

其中，PR(Vi)为节点Vi的PageRank值;d为阻尼因子，1-d是随机游走到其它节点的概率，一般取1-d=0.15；In(Vi)表示指向节点Vi的所有节点的集合，Out(Vj)表示节点vj所有指向节点的集合。由于对节点计算PageRank值时参考了节点与其邻居，一个节点的邻节点越重要，则这个节点越重要。计算的过程相比于度中心性具有较高的复杂度，整个算法的运行时间将会较大，因此在较大规模的网络中使用节点的度中心性来选择割点更为合适。

所以基于割点移除的节点重要性方法由以下几个步骤组成：

1)构建候选移除节点集合

取当前图的最大连通分量作为待操作子图。利用Tarjan算法判断并求取当前待操作子图中所含有的割点，若当前子图为点双连通分量则不存在割点，如果含有割点则将所有割点放入候选移除节点集合AP

AP={n|n∈V且n为割点}

(4)

2)获得待移除节点

将当前所有割点中具有度中心性最高的节点作为移除的节点，考虑到不是所有的图都具有割点，因此若图中无割点，则直接将该子图中度中心性最高的节点作为移除节点。

图3 割点移除过程示意图

如图3所示，移除割点a和割点d都可以破坏网络的结构，使网络的最大联通分量规模减少，但是，移除割点a后，最大联通分量规模减少的更多，割点a比割点d更接近网络的核心位置。通常，在具有多个割点的情况下，度中心性更高的节点更接近网络的中心，所以在移除节点时优先选择度中心性更高的割点。移除节点的选择如式(5)所示

(5)

其中AP为割点集，V为当前子图下节点集。

3)移除节点

移除步骤1)步得到的节点。得到不含有此节点子图。

具体而言，取G的真子图G’使得G’符合以下要求

G′(V′，E′)⊆G(V，E)

(6)

其中V’，E’分别表示移除节点后的节点集合与边集合，ω(Nr)表示取Nr所有的连边，其取值由以下公式决定

E′=E-ω(Nr)

(7)

V′={n|n∈V且n≠Nr}

(8)

4)更新当前操作子图

将移除节点后的图中最大联通分量作为新一轮移除的图。

重复1)-4)直到整个图中的最大联通分量不再具有边。

根据前文提到的步骤，本文所提出的节点重要度排序算法APRRank核心部分伪代码如下所示。

代码1 APRRank算法主要工作流程

Input：Graph

Output：节点排序以及评分 Score

1：FUNCTION APRRank(Graph)

2： LC ←σ(Graph)

3： APList←Tarjan(LC)

4： WHILE |LC.edges|≠ 0 do

5： IF APList ≠ ∅:

6： node ←MAX(DC(APList))

7： ELSE

8： node ←MAX(DC(LC))

9： END IF

10： LC ← REMOVE(LC，node)

11： LC ←σ(LC)

12： Insert node into Score

13： APList←Tarjan(LC)

14： END WHILE

15： RETURN Scor

16：END FUNCTION

4 仿真研究

为评价基于割点移除节点重要性排序算法的有效性，本文在多个真实的，规模不一，差异较大的社交网络中进行了仿真，实验数据来自NR[13]提供的开源社交关系网络。

其中Caltech36，simmons81属于Facebook网络数据集，wiki-Vote数据集包含从维基百科建立到2008年1月的所有投票链接数据。Advogato是某社交平台信任关系网络。仿真相关统计指标如下：

表1 仿真数据相关统计情况说明

4.1 结果对比

为了比较不同方法的重要节点排序结果，本文利用PageRank算法(PR)，度中心性(DC)，接近中心性(CC)，介数中心性(BC)，以及综合评估方法TOPSIS，对上述网络进行仿真，得到排名前十的重要节点。结果如表所示：

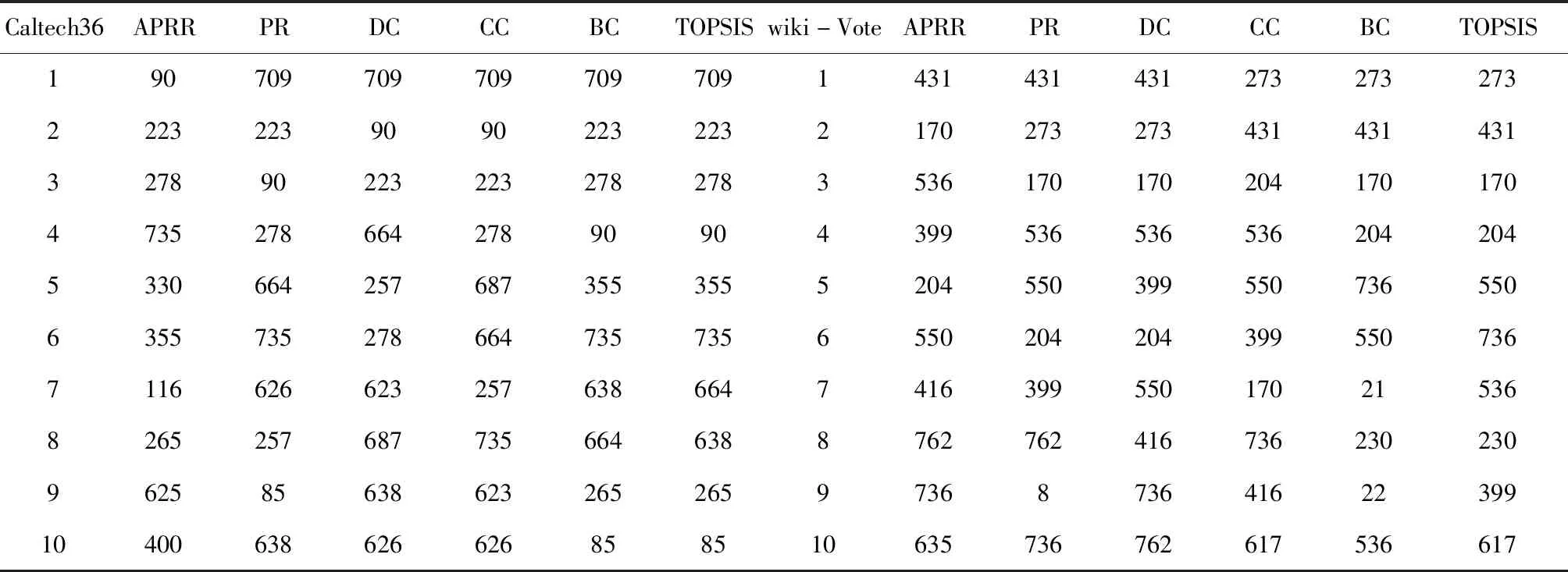
表2(a) Caltech36与wiki-Vote网络各方法排序结果

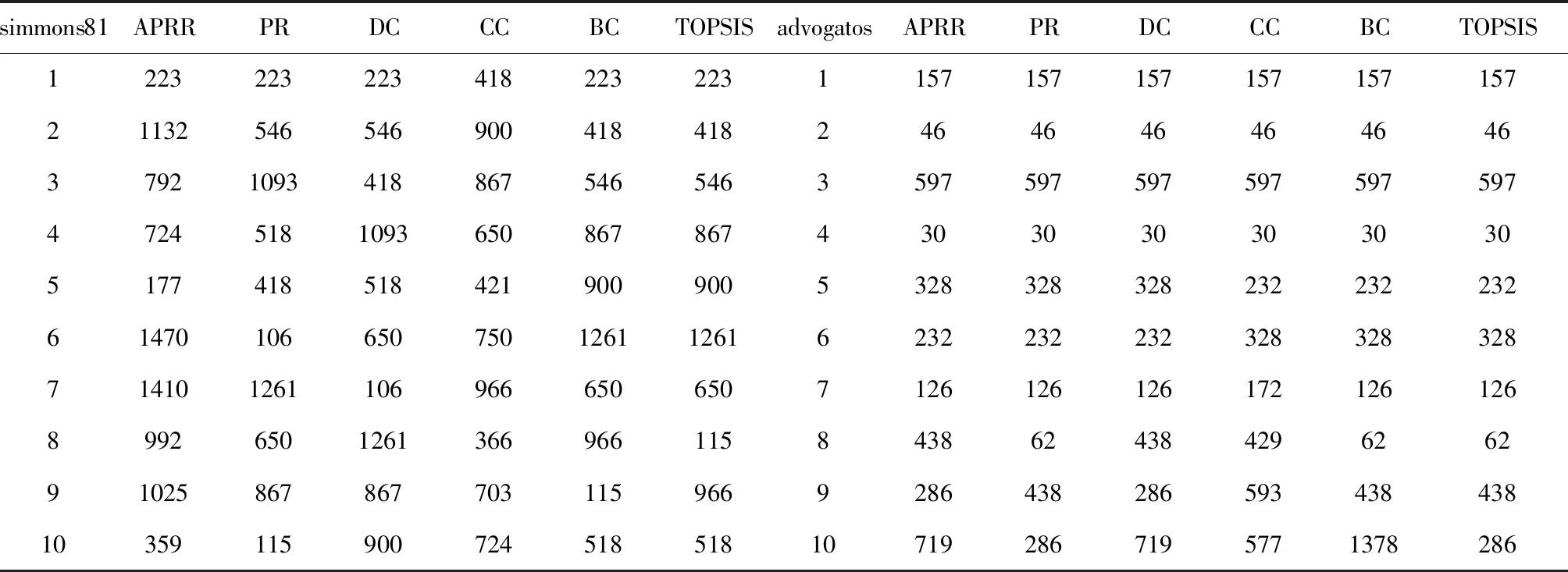
表2(b) simmons81与advogatos网络各方法排序结果

各个方法排序侧重的依据不同，所以排序的结果也存在一定的差异，以Caltech36网络为例，排名第一的节点就产生了不同，除了APRRank其它的方法均为709，APRRank方法首先关注的是割点，在此网络中的度中心性最高的割点为90号，因此将90号节点作为排名第一的节点，在移除90号节点后，产生了多个联通分量，在新的最大联通分量中再进行对度中心性最高的割点便可得到223号节点。用APRRank排序是一个动态的过程，所以后续的排列也会和其它方法有较大的不同。

4.2 鲁棒性测试

为了具体衡量本文算法的效果，本文对上述网络分别使用中心性方法，PageRank方法，TOPSIS方法，以及APRR算法对五个不同网络进行网络鲁棒性仿真。

在网络鲁棒性仿真中，首先，计算网络中所有顶点的重要性，然后按照中心度量的顺序从最高到最低去除指定的节点，即按照排序顺序依次移除节点。为了考察攻击一部分节点使之失去效果后，即移除该节点，网络整体结构和功能上的变化，本文绘制了最大联通分量相对规模(σ)随各个方法排序结果按顺序移除节点比例(n)的变化曲线。计算方式如式(9)所示

(9)

其中G为当前子图，LC为当前子图最大联通分量。

Swami等人[14]应用4种不同的方法对节点进行排序并绘制鲁棒性测试曲线。绘制曲线可以准确的得到依次移除这些节点对图的影响过程，从而间衡量了节点重要性排序的效果。纵坐标为最大联通分量规模占比，横坐标为移除节点占比。若曲线降低的速度越快，则认为网络在移除相应的节点后网络功能衰减的越快，同时也就意味着这样的节点重要性排序结果在鲁棒性测试中效果越好。

图5 Soc-wiki-Vote鲁棒性曲线

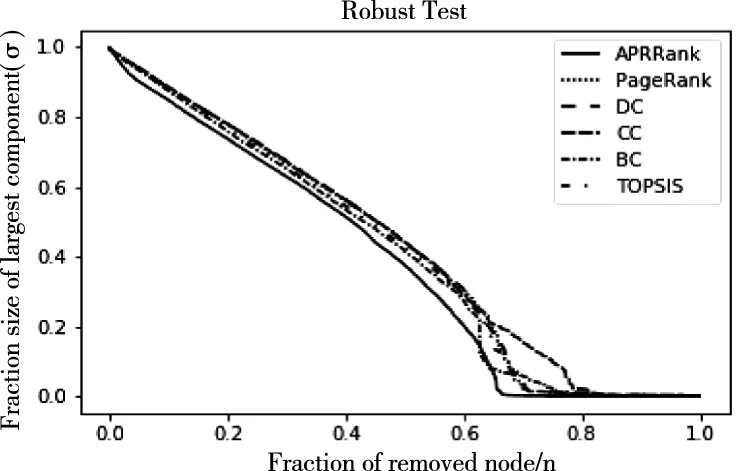
图6 Socfb-simmons81鲁棒性曲线

图7 Socfb-Caltech36鲁棒性曲线

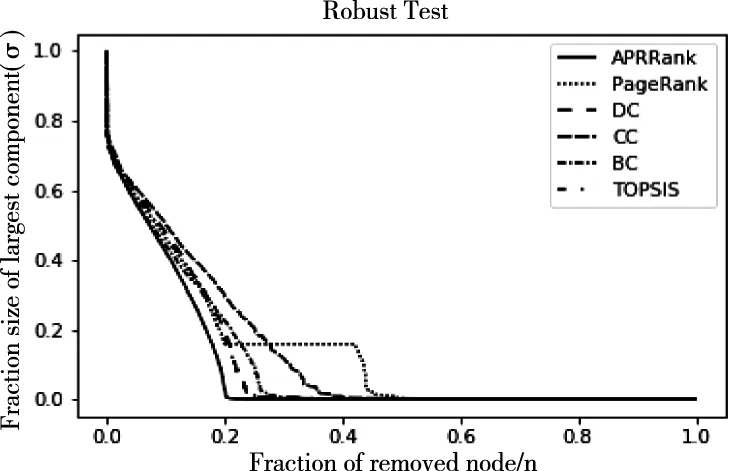
图8 Soc-advogatos鲁棒性曲线

如图5-8所示，在鲁棒性测试中，实线部分为APRR方法，其它方法均为虚线。可以从图中看出，APRRank方法在规模不一的网络中都有较好的效果，按照APRRank方法得到的节点重要性序列进行依次移除仿真社交网络中的节点，4个社交网络最大连通分量的规模衰减效果都最为明显，绝大大分都处于其它曲线下方，可以使网络更快的碎片化。因此在社交网络中如果按照APRRank方法得到序列进行针对性攻击，其打击效果要好于常见中心性方法，PR方法以及综合性评估方法TOPSIS，可以更加迅速的破坏网络，瓦解网络，证明了APRRank算法的有效性。

5 结束语

本文提出了一种基于割点移除的社交网络重要节点评估方法，对复杂网络中最大联通分量里的度数高并且具备割点角色的节点进行了依次移除，并且按移除顺序作为节点重要性的排序。在此基础之上，本文对四个规模不一网络进行了鲁棒性仿真，实验结果表明，按照本文所提出的APRRank方法依次攻击相应的节点，可以更快的破坏网络的整体功能，让网络的破碎程度更大，证实了本文所提方法的有效性。

但是，本文所提方法还有一定的不足，下一步工作将重点关注如何更快的找到割点并移除，提升算法的速度。