基于不相关性检验的大数据异常抽取算法
2021-11-17谌裕勇陆兴华
谌裕勇,陆兴华
(广东工业大学华立学院,广东 广州 511325)
1 引言
计算机与互联网技术的广泛应用,使得各行业数据均呈爆炸性增长,庞大数据量已成为互联网重要研究目标之一[1]。数据抽取可实现海量数据内高效获取目标信息与知识,数据规模大、多样化是大数据的基本特征。海量数据内通常会存在少量数据对象与正常数据期望行为不同,通常将其称为大数据的异常值[2],恰当处理此类异常数据是维护大数据正常应用的必要途径。在此背景下,有许多专家对此问题进行研究,得到了一些较好成果。
文献[3]按照异常网络数据的混合分类属性完成大数据之间的相似度分析,获得数值属性特征与分类属性特征。运用联合关联规则对异常网络数据完成模糊融合,建立异常网络数据分类模糊集,在模糊数据集中完成数据混合加权与自适应分块匹配,提取异常数据弱关联化特征量,将提取的特征量输入到模糊神经网络分类器中实行数据分类识别,达到异常大数据目标挖掘。但由于大数据具有较高随机性,导致该方法的应用准确性不高。文献[4]提出大数据集合中冗余特征排除的聚类算法。利用一致性聚类算法抽取各种子集样本,完成大数据冗余特征排除,并得到排除冗余特征的大数据集聚类结果。采用特征聚类和随机子空间的识别算法,聚类大数据集合冗余特征,实现大数据异常的抽取。但该方法存在计算开销大及复杂度高等问题。
针对以上传统方法存在的问题,提出大数据异常抽取算法。对大数据流量分流处理,利用预处理端与储存端监测异常数据风险,有效降低大数据异常抽取的耗时。基于此,构建不相关性检验模型,引入模糊遗传方法算出异常数据流汇聚于多层空间内的模糊聚类中心,耦合关联训练集与所属类型,大大增加大数据异常抽取的精度,最终实现高精度大数据异常抽取。实验结果验证了所提方法能够低耗时、高精度的完成大数据的异常抽取。
2 大数据全局趋势分析
在完成大数据异常抽取过程中,大数据全局风险趋势分析是必要的[5],可有效估计大数据异常概率。建立基于Hadoop的大数据平台异常风险监测平台,预判断大数据是否存在异常问题,判别大数据安全等级,为不相关数据分析提供借鉴。
大数据具有体量庞大、类别复杂等特征,所以平台在Hadoop操作原理前提下进行规划,采用Map/Reduce分布式形态对大数据实时操作,过程如图1所示。图中将大数据内的异常数据监测任务划分成多类子任务,各类子任务依次经过一个节点,最终将结果传输至数据库管理节点内,主管理节点融合所有结果后,所得数据即为异常风险数据监测成果。

图1 Hadoop操作示意图
图1中大数据平台通过计算端与操控端构成,利用接口1将其相连到同一个路径,增强大数据传输适用性。接口2即为平台作为操控端输入网络参变量重置标准,SDN控制器对大数据的控制就是将参变量重置后的大数据流进行分流,将大数据依次传输至监测板块,使得监测板块能实时精准的异常数据风险趋势监测。监测板块内包含预处理端与储存端,并设定预警电路与缓冲电路,增强系统对风险趋势预测可靠性。本文运用最小二乘向量机监测大数据平台异常风险[6-7],设定大数据平台内的异常数据监测样本集合为
D={(xk,yk)|k=1,2,…,N}
(1)
径向基函数为核函数ψ(·,·),运算过程为

(2)
其中,σ代表径向基函数宽度参变量。
最小二乘支持向量机的最佳决策函数运算方程是

(3)
其中,γ表示内正则化参变量。
在式(3)内引入拉格朗日乘子方法,得到:
L(w,b,e,a)=φ(w,b,e)=akyk[wTφ(xk)+b]-1+ek
(4)
其中,ak∈R表示拉格朗日乘子。
按照Mercer定理可知Ω=ZZT,即:
Ωkl=yky1φT(xl)=yky1Ψ(xk,xl)
(5)
将最小二乘支持向量机最佳决策函数转换为式(12),实现大数据风险趋势计算全过程。
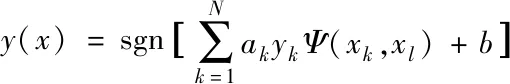
(6)
3 大数据异常抽取算法
3.1 构建不相关性检验模型
通过上述过程计算出大数据具有异常风险状态后,为获得更加准确的大数据不相关数据特征,代入Fisher函数等价模式[8],构建不相关性检验模型。若样本类间散布矩阵是Sb,类内散布矩阵是Sw,那么Fisher函数表达式为

(7)
不相关性检验模型是为了探寻不相关检验向量而提出的,其目标是找出符合Si共轭正交条件,同时让Fisher函数完成极值最佳检验向量φ1,φ2,…,φd。在真实操作中,第一个检验向量是Fisher最优检验矢量。若现阶段k个检验向量φ1,…,φk被求出后,则第k+1个不相关性检验向量φk+1可由式(8)进行求解

(8)
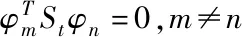
以式(8)为前提,可明确第k+1个不相关性检验向量是以下广义特征方程最大特征值相对的特征矢量,记作
PSbφ=λSwφ
(9)
式中
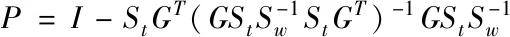
(10)

(11)
I=diag{1,1,…,1}
(12)
在不相关性检验向量的运算表达式中可知,各个检验向量相对的p的运算均牵涉数量较多的矩阵计算,中间还包含较多矩阵逆运算。在大数据不相关性检验向量数量较多时[9],求解全部检验向量的计算代价很高。下面改进不相关性检验模型,以便解决计算代价高的问题。
式(13)是Fisher函数表达式的等价模式,记作

(13)
按照Fisher检验分析定理,应当计算出让J′(φ)得到极值的φ,通常把J′(φ)模式的极值问题和以下广义特征方程问题进行统一解决
Sbφ=λStφ
(14)
利用式(14)来描述Fisher函数,那么不相关性检验向量集问题模型就变换成以下问题模型:首个检验向量是式(14)最大特征值相对的特征矢量,第r+1个不相关检验向量通过式(15)求解,呈现大数据中数据实时状态

(15)
3.2 基于模糊遗传的大数据异常抽取算法
不相关性检验模型为大数据异常抽取提供精准的数据特征依据,下面采用模糊遗传算法实现大数据异常抽取目标,为大数据安全及数据平稳传输发挥积极作用。
传统方法使用遗传算法对大数据异常抽取的具体操作是设计一个种群适应度函数及各种遗传操作,包含交叉变异、收敛条件等[10]。
如果在c个类型相对的样本类型ωm是已知值,假设被求解的参数是Q,Xi是参数Q空间内的解,针对各个Xi相对的函数,fi为Xi的适应度函数,所获得的最佳解即为让xm和函数值fm均是最大或最小的值。
遗传算法内的染色体被划分成三个子模块,分别是连接顺序和网络节点挑选、副本关联挑选及网络半连接控制。使用匀称随机方法生成二个交叉点,然后把二个交叉点交叉过程中涵盖的区域设定成匹配范围,将其记作
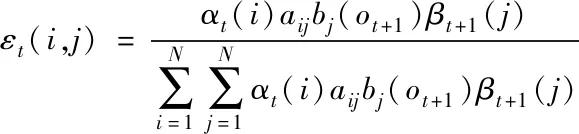
(16)
其中,αt(i)是大数据内异常数据的监测节点信道误差,bj(ot+1)代表平均值是0,方差是1的复高斯过程。
设定异常数据节点数据融合滤波器系统函数是
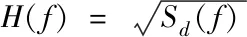
(17)
其中,Sd(f)表示多普勒功率谱。
使用遗传算法应用到异常数据特征迭代过程中,会产生一个种群,此时适应度强、遗传性质较优的染色体变成算法的首要挑选目标[11]。本文设计一种模糊遗传方式完成异常数据特征选择,遗传迭代查询散布解析式为
pri(t)=p(t)*hi(t)+npi(t)
(18)
其中,hi(t)是p(t)在大数据异常特征抽取时的变异矢量。算出大数据内异常数据特征响应函数为

(19)


(20)
使用模糊遗传方法算出异常数据流汇聚于多层空间内的模糊聚类中心,那么j为i的激活因子,得到
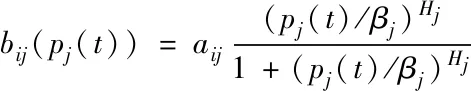
(21)
把训练集和其所属类型实时关联,获得异常数据属性集分类的信息增益解析式

(22)
通过式(22)可知,使用模糊遗传算法完成大数据异常抽取时,能够把随机变异转换为换位控制,两个等位基因相互交换,数据染色体交叉之后无需修复。副本选择基因与半连接基因全部运用匀称杂交方法,增强异常数据抽取性能。

异常数据特征对最小二乘支持向量机性能影响较多,对其余特征影响较少,采取归一化手段清除此类不良影响[12],具体过程为

(23)
其中,n代表训练样本数量,xstd代表标准差。
使用模糊数学隶属函数值方法抽取大数据内的异常数据,隶属函数值运算公式为
R(Xi)=(Xi-Xmin)/(Xmax-Xmin)
(24)
其中,Xi是指标检测值,Xmax、Xmin依次是数据异常某项指标的最大值与最小值。
利用以上过程即可完成准确的大数据异常抽取,为数据流的正常使用提供有效解决途径。
4 实验分析
为检验所提方法性能,在Cslogs大数据集上对所提方法与文献[3]、文献[4]算法进行实验对比。实验在Windows 10环境中进行,计算机CPU是Pentium(R)DualCore T4300@2.10GHz,内存2.0GB,硬盘是320GB。
4.1 不同算法的大数据异常抽取效率对比
在输入数据量固定时,按照最小支持度改变量,对比三种方法性能。关于大数据异常抽取算法,支持度适应能力是一个关键指标。图2是所提算法与文献算法的大数据异常抽取运行效率对比。
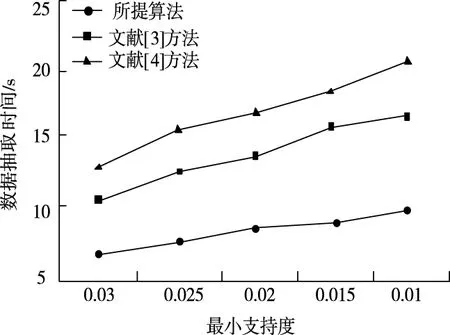
图2 三种方法大数据异常抽取时间对比
从图2中可知,最小支持度从0.03减少至0.01,以抽取效率角度而言,所提方法在大数据异常抽取时的消耗时长远低于文献[3]及文献[4]方法,原因在于所提方法利用不相关性检验模型,很好地展现数据真实状态,有效提高大数据异常抽取速率。
4.2 不同算法的大数据异常抽取准确度对比
为验证所提算法的大数据异常抽取准确性,随机选取大数据集合(来源:caesar0301/awesome-public-datasets·GitHub),对大数据训练集进行可视化区域划分,利用思迈特软件对大数据进行可视化处理,得到异常数据较多区域,以60cm×70cm网格为实验区域,大数据中的异常数据用星状表示,具体实验结果如图3。
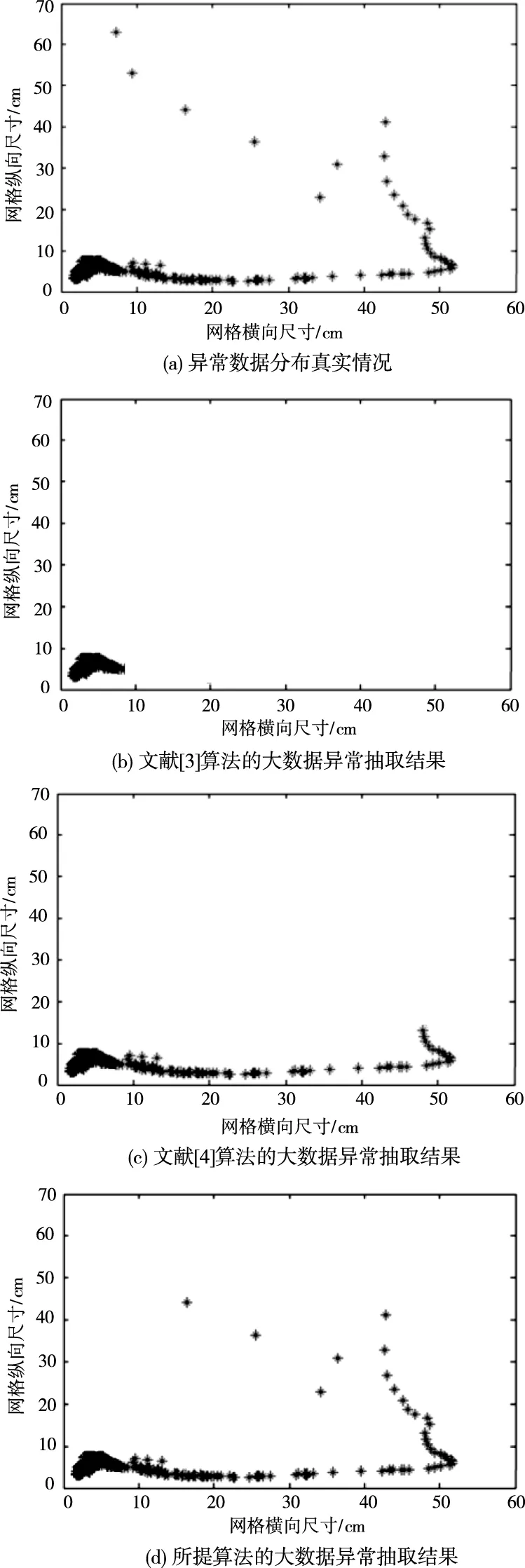
图3 不同算法的大数据异常抽取对比测试
由图3的实验结果可知,在大数据的实验测试区域内,文献[3]算法和文献[4]算法只能抽取出较为密集的异常数据区域,抽取结果与实际情况相差较大,说明传统算法的异常数据抽取误差偏大。相比之下,所提方法的大数据异常抽取结果与实际情况基本一致,进一步验证了所提算法的应用有效性。
5 结论
1)为提升大数据异常抽取时效性与准确性,引入不相关性检验,设计新的大数据异常抽取算法。
2)实验结果显示:在最小支持度从0.03减少至0.01过程中,所提方法的耗时由7s增加到了9s,与传统方法相比耗时有明显下降。且所提方法的大数据异常抽取结果与实际情况基本一致。以上实验结果验证了所提方法能够高速率、高精度的完成大数据异常抽取,应用鲁棒性强,有效增强了大数据异常辨识能力。
3)但在本次研究中,对大数据异常风险产生原因研究不够具体,不能从根源减少问题的发生,下一步会着重在此方面进行探究。
