异时滞分数阶细胞神经网络的电路设计与仿真
2021-11-17张梓涛
张梓涛,袁 晓
(四川大学电子信息学院,四川成都 610064)
1 引言
细胞神经网络(Celluar Neural Networks,CNN)[1]是20世纪80年代后期由Chua和Yang提出并建立.细胞神经网络的出现促进了人工智能的发展,同时混沌非线性学领域也得到了很大的发展.混沌现象是自然界中普遍存在的一种宏观无序、微观有序的非线性现象,亦是确定性非线性系统的一种复杂非周期的时间演化现象.由于混沌信号的高随机性、复杂性、初值敏感性,以及确定性系统方程的易实现性[2],使得混沌在非线性科学、保密通信、图像处理、信号检测等方向具有广泛的研究和应用价值[3]。
分数阶系统能表现神经网络的联想、记忆、遗传等复杂特性,相比整数阶更能揭示复杂多变系统其固有特征和非线性规律[4,5]。
现实生活中任何系统在进行信号传输时都会存在一定的时滞,且有些系统加入时滞后会发生根本性的变化[6],因此时间延迟这一因素在具体工程应用中显得十分重要.本文提出一种异时滞分数阶细胞神经网络模型,研究不同时延下系统的混沌状态,发现通过改变部分参数值可使系统具有相似的混沌吸引子.笔者研究了0.02ms、0.04ms和0.08ms不同时滞组合下分数阶CNN系统电路的混沌特性,发现通过改变某个电阻的值,可使其Multisim仿真结果与数值计算具有相似的混沌相图,从而证实了设计理念的正确性和现实可行性.
2 分数阶CNN模型及数值仿真
CNN是每一个相同的细胞元在空间上与相邻的细胞元连接形成的拓扑结构,网络中每个细胞元都有相应的输入输出和非线性动力学特性[7],是一种模拟非线性、实时并行处理的列阵结构.考虑一般分数阶细胞神经网络模型的状态方程[8]

(1)
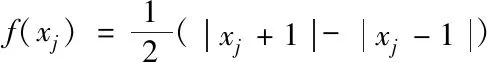
(2)
其中,xj为第j个细胞的状态变量;n为细胞单元的个数;q为微分算子阶数;ajk、sjl分别表示反馈控制系数和状态控制系数;f(xj)为细胞xj的输出;Ij为细胞的阀值.
如果令n=3,则系统(1)变为:
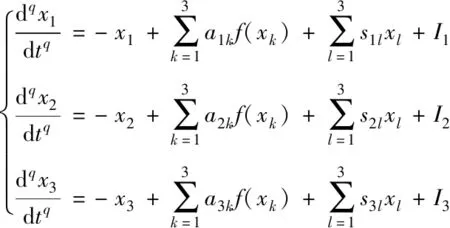
(3)
令系数矩阵
根据混沌吸引子理论,若某一点附近的相体积随时间的变化而缩小,则称为吸引子.对于系统(3),取q=1,α=1有
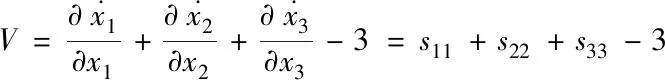
(4)
其中s11=-1.5,s22=0,s33=1,带入得∇V<0,因此系统(3)是一个耗散系统,耗散系统是混沌吸引子存在的前提条件。
当q=1,α=1,Ij=0,令系统初值分别为x1(0)=0.1,x2(0)=0.1,x3(0)=0.2,步长为0.005,步数为10000.对系统(3)进行Matlab数值仿真,利用Jacobi方法计算得到Lyapunov指数
L1=1.5815,L2=-2.5466,L3=3.9509
Lyapunov维数:
其中最大Lyapunov指数L3大于零,因此理论上判定该系统具有混沌特性[9].
进一步取q=0.9,α=0.05,用Matlab进行数值仿真得到的混沌相图如图1,可见该分数阶CNN系统产生了双螺旋混沌奇异吸引子,从而证实该系统能产生混沌现象。
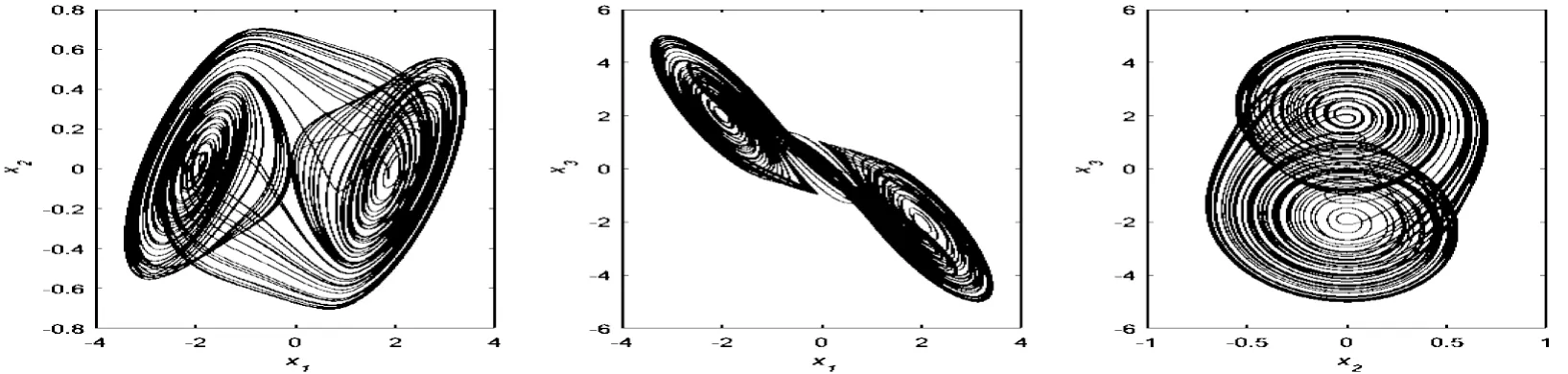
图1 q=0.9,α=0.05时系统(3)的混沌相图
3 异时滞分数阶CNN电路仿真
根据系统模型的状态方程(1),提出带时延的分数阶CNN系统方程

(5)
其中bjk为时滞反馈控制系数,τj为第j个细胞单元的时延,其余参数含义与式(1)一致.
为了降低系统复杂度,考虑纯时滞系统模型,其反馈控制系数全为零,时滞反馈控制系数与式(1)反馈控制系数相同,状态控制系数不变,即
取n=3,q=0.9,Ij=0,带入方程(5)
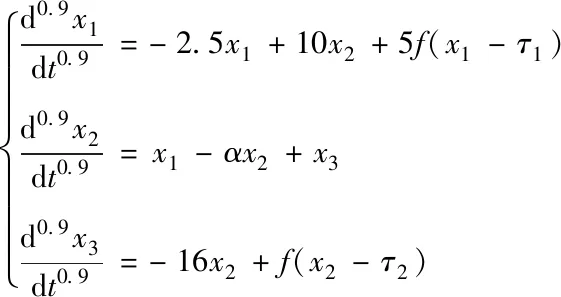
(6)
令方程(6)中τ1、τ2为时滞常数0.02ms、0.04ms和0.08ms的两两组合,根据排列组合公式,总共有6种组合情况,由于篇幅有限,仅考虑以下三种时滞情况,研究系统电路在不同情况下的混沌特性
异时滞分数阶CNN整体电路的设计采用有源运算放大器、线性电阻、线性电容、二极管等元器件,结合电路基本理论综合实现.电路主要由输出函数电路、分数阶电路、时滞电路等单元模块组成.
3.1 输出函数电路
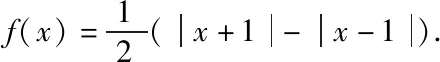
其中绝对值运算电路实现如图2所示[10],根据电路叠加原理,端口2的输出电压表达式为y=2(x1-x2)+x1.若x1<0,则二极管D1、D2截止,运放U1虚短,此时x2=2x1,即y=-x1;若x1>0,则二极管D1、D2导通,此时x2=x1,即y=x1,由此实现绝对值函数y=|x1|。
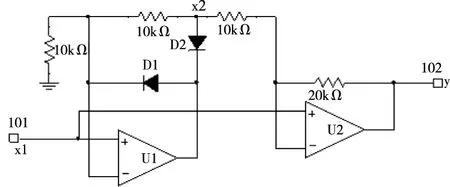
图2 绝对值运算电路
根据图2绝对值运算电路,再用运算放大器实现基本加减法,得输出函数f(x)的电路原理图及测试波形,如图3(a)-(c)。
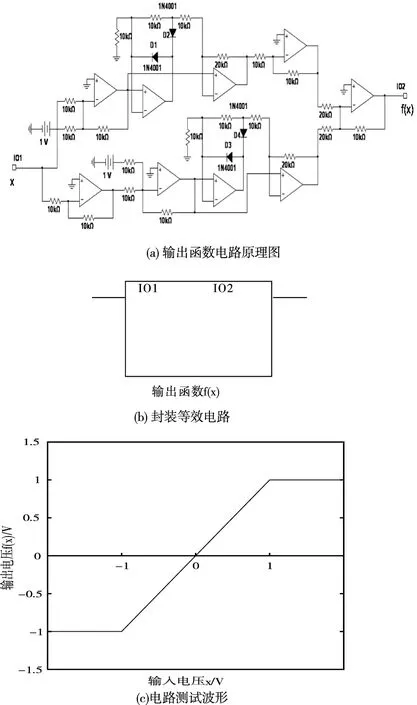
图3 f(x)电路原理图及测试波形
3.2 分数阶电路
截止目前具有分数阶运算功能的无源电路已有很多种,如链型、树形、Oldham链型、Liu-Kplan分形链型、Carlson分形格型、Morrison分形梯型等[11-14],本文使用简单的链型电路[15,16],电路结构如图4。根据结构图可直接写出端口1和端口2之间等效电路的复频域表达式
(7)
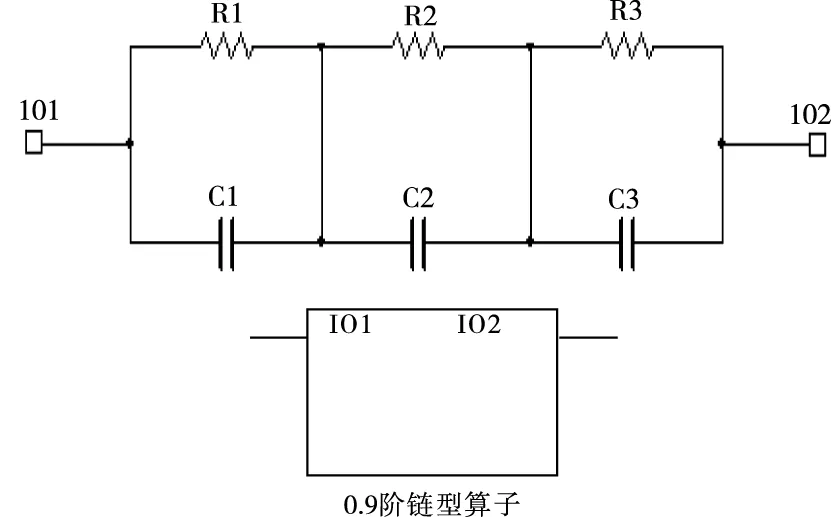
图4 分数阶电路原理图及封装
再由整数阶逼近分数阶算子的公式[17],当运算阶次q=0.9时
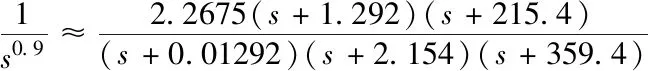
(8)
对H(s)做基本的数学变形再与式(8)比较,通过对比即可求出各元件值
3.3 时滞电路
目前能产生时延的方法主要有LCL滤波器、贝塞尔滤波器、数字电路和组通式器件等[18].由于本文设计的网络系统的工作频率位于低频带(约100Hz),因此选择结构更为简单的LCL低通滤波器来产生时延,LCL电路如图5。

图5 LCL电路原理图
根据群时延与相位的关系,群时延是系统在某频率处的相位对频率的变化率,即相频特性在某频率点的负斜率值。
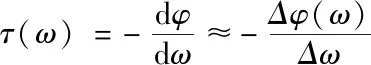
(9)
本文所构造的CNN系统电路的工作频率经测量在100Hz左右,因此需构造在该频率点附近的时滞。值得注意的是,为了获得更稳定的频率特性曲线,可在图5 LCL滤波电路两端加上相应匹配电阻,但匹配电阻的引入会对输入信号造成一定程度的衰减,因此需用运算放大器进行增益调整。电路原理图如图6。时滞常数τ可以通过调节电感值L和电容值C来改变,运算放大器用来调节输出增益。
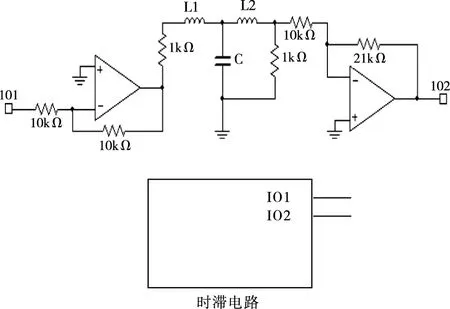
图6 时滞电路原理图及封装
具体考虑系统方程(6)中的三种时滞情况,即需分别构造工作在100Hz频率附近的0.02ms、0.04ms和0.08ms三种时滞电路.以τ=0.02ms为例,可取L1=L2=10mH,C=20nF。在Multisim中仿真得到0.02ms时滞电路的幅频特性和相频特性如图7。

图7 0.02ms时滞电路频率响应
由图7(a)幅频特性可以看出,当输入信号频率为100Hz时,输出增益为0dB,可见该时滞电路对系统信号不产生任何幅度的改变。又由群时延的概念,相位对频率的导数即为该点的时延值,对应到相频特性曲线为该点切线的负斜率,可求[50Hz,150Hz]之间相频特性的斜率作为系统的平均时延。在图7(b)相频特性中,频率为50Hz时,相位角测得为-0.36度;频率为150Hz时,相位角测得为-1.081度,因此频率范围在[50Hz,150Hz]之间直线的斜率(时滞)

(10)
测试输入频率100Hz的正弦信号,波形如图8,红线为输入蓝线为输出。仿真结果证实该电路对频率为100Hz的输入信号产生0.02ms的时延,且信号幅度基本不变。
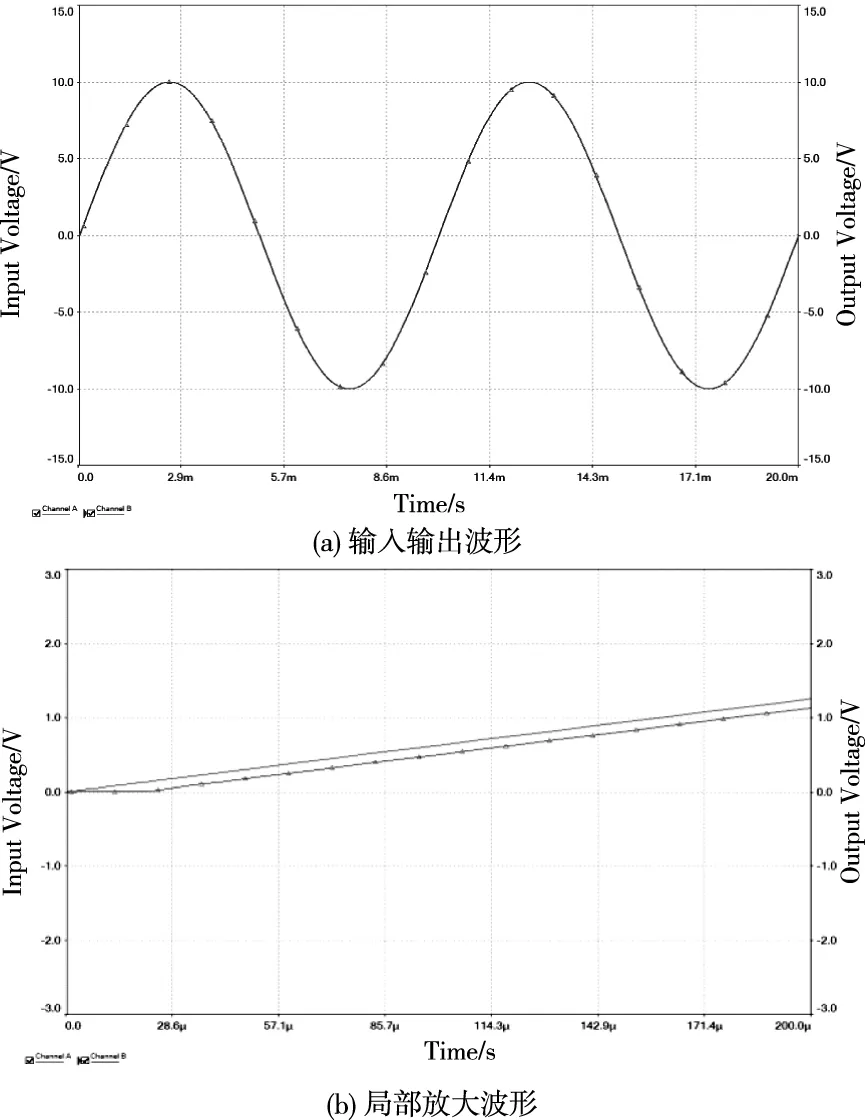
图8 0.02ms时滞电路测试波形
同理可设计0.04ms和0.08ms的时滞电路,当τ=0.04ms时,取L1=L2=25mH,C=30nF;当τ=0.08ms时,取L1=L2=50mH,C=58nF.各时滞单元模块的电路封装如图9。

图9 各时滞电路模块封装图
3.4 异时滞分数阶CNN电路及仿真
使用模拟电路中的反向加法电路、反向积分电路、反相电路等电路理论构造三阶细胞神经网络的电路模型,再结合输出函数模块、分数阶模块和时滞模块,构成带时滞的分数阶CNN整体电路,整体电路如图10(a)。其阶数q=0.9,端口1、2和端口3、4分别接时滞τ1和τ2的单元电路,端口5、6、7分别对应细胞元x1,x2,x3的状态输出,电阻Ra用来调节系统(6)中的系数α。图10(b)为封装电路,图10(c)为异时滞测试电路。
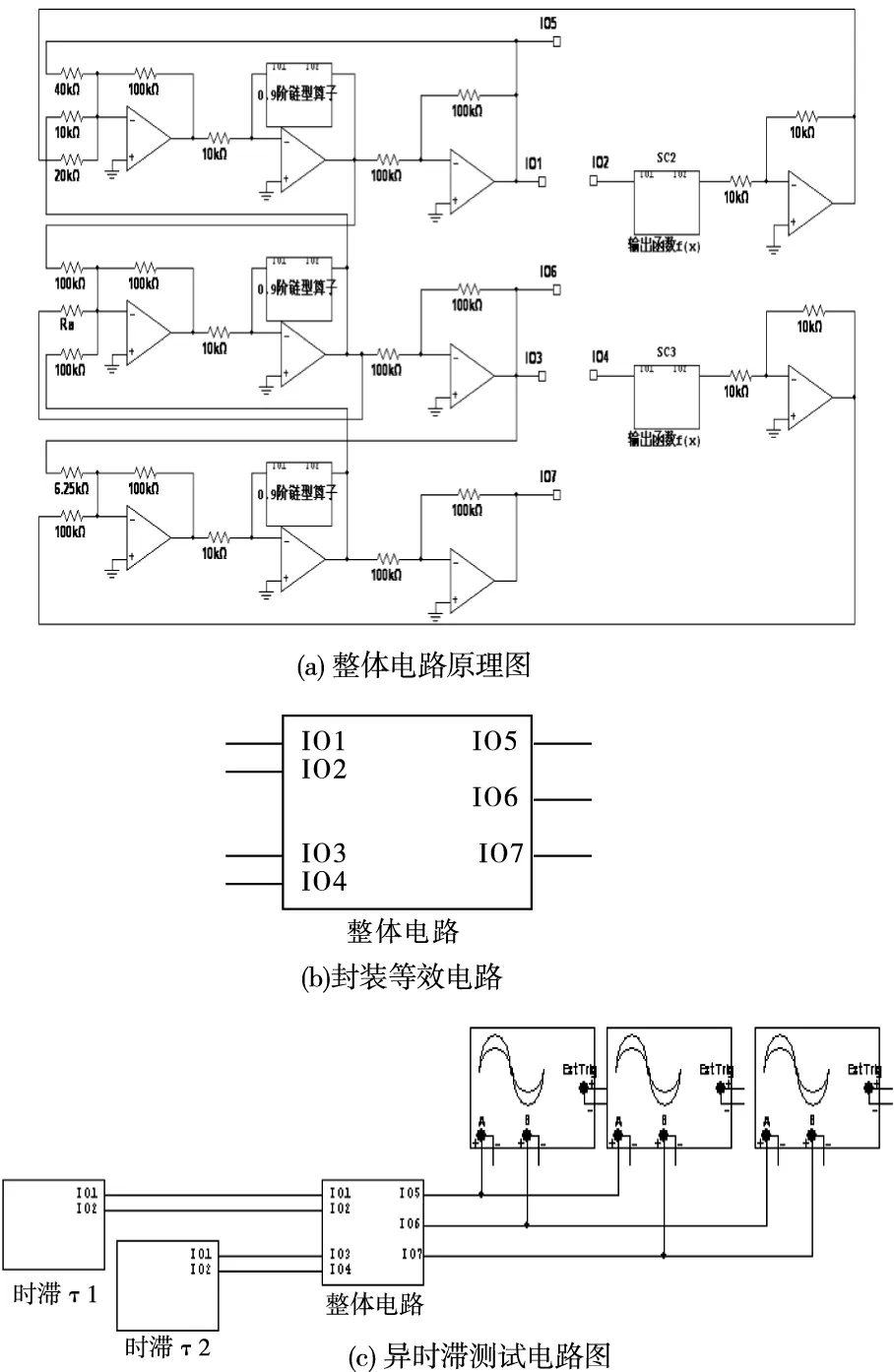
图10 异时滞分数阶CNN电路仿真
对图10(c)进行仿真测试,当时滞τ1,τ2为前文提及的三种情况时,取图10(a)中电阻Ra分别为1720kΩ,1360kΩ,840kΩ。对应方程(6)中的系数α分别约为0.06,0.07和0.12,用示波器观测细胞[x1,x2],[x1,x3],[x2,x3]的状态输出,输出相图见表1。
3.5 仿真结果对比分析
比较表1的Multisim电路仿真结果(带时滞)和图1的Matlab数值仿真结果(不带时滞),不难发现其波形十分吻合,因此该电路仿真结果是有效的.时滞分数阶CNN系统相比无时滞系统具有更大的普适性,且时滞常数τ1,τ2发生变化时,电阻Ra可调又表明该系统具有更好的鲁棒性,证实了该设计理念的正确性和物理可实现性。
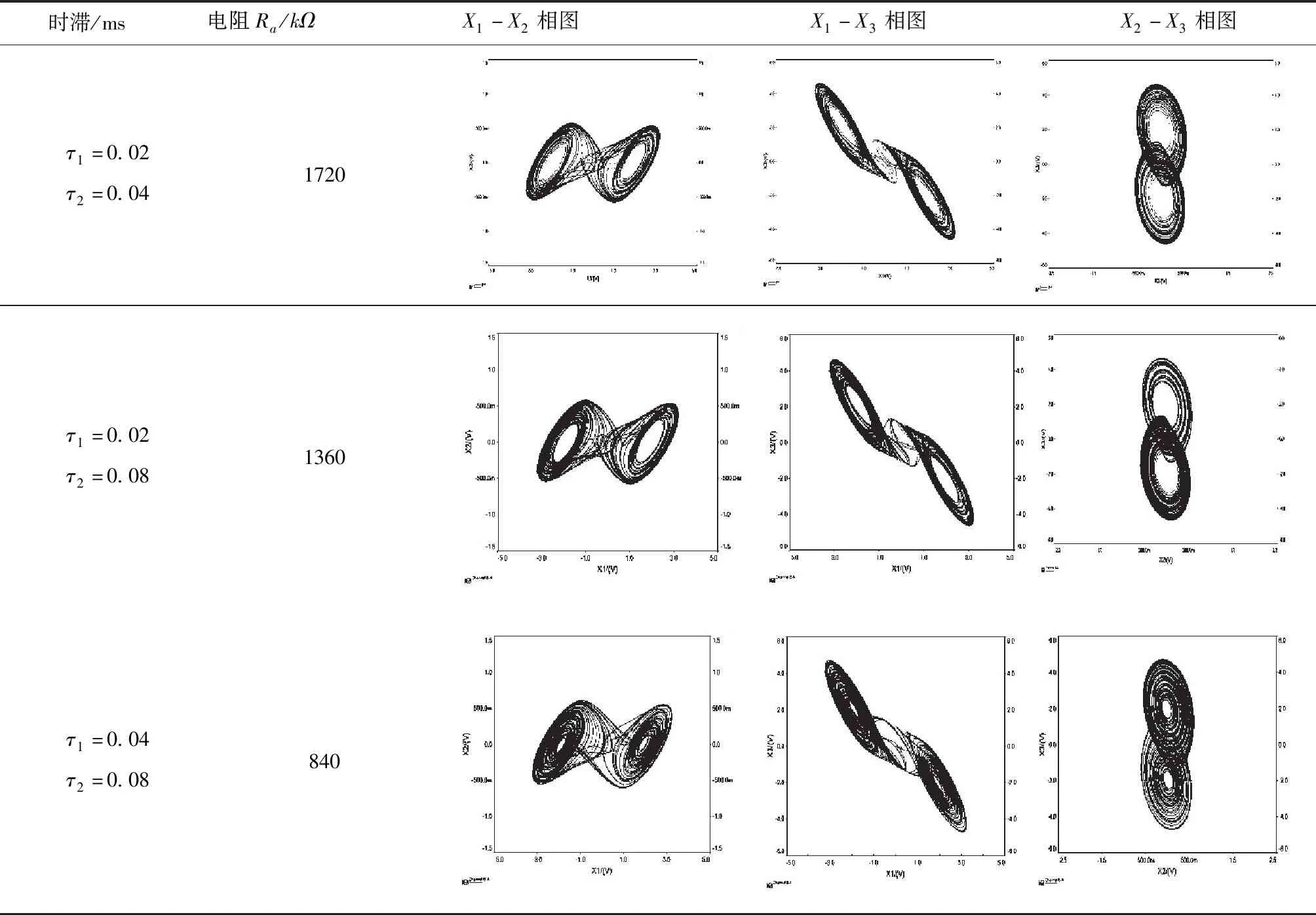
表1 电阻Ra可调节的异时滞CNN电路仿真
4 结论
1)基于细胞神经网络理论,提出时滞分数阶CNN系统模型,证实了时滞分数阶CNN的电路可实现性.
2)对于异时滞分数阶CNN系统电路,通过改变部分元件参数值可使系统具有相似的混沌特性,证实了该系统具有较好的鲁棒性和稳定性.
3)本文研究在固定时延值下的分数阶CNN系统,但工程上使用时,往往时延值会随时间变化而变化,因此对于时延为τ(t)的CNN系统有待进一步研究.
