面向温度变化的相机光学系统参数模型研究

刘丽伟，赵子君，朱绪康，许 倩

(长春工业大学计算机科学与工程学院，吉林 长春 130012)

1 引言

随着航空航天光学仪器分辨力的提高，高空或空间热环境的温度变化会引起图像发生偏移，对光学系统成像质量造成的影响已经不容忽视。温度变化对相机光学系统的影响主要和三个方面有关:第一，光学材料的折射率会随温度的变化而改变，此现象致使光学系统的焦距、主点位置以及畸变系数发生变化;第二，温度的变化会导致光学系统不同组件(如探测器靶面、镜头、支撑结构等)的膨胀或收缩，从而改变镜头的厚度、曲率半径和表面形状，进而导致焦距、主点位置的变化；第三，由于镜筒材料的热膨胀和冷收缩，光学元件之间的间距会发生变化[1，2]。因此，在光学系统的设计中，降低温度变化的影响是十分必要的，尤其是对于精度要求较高的光学系统。

对于此问题的研究起源于上世纪40年代，J.W.Perry等人研究了均匀温度变化对光学系统成像质量的影响[3]。随后有一些研究人员通过有限元分析的方法讨论了温度变化对光学系统材料特性、结构形变以及像面位移等问题进行了分析[4，5]。由于这些研究目的是为无热化技术[6]提供理论支撑，虽然无热化成像技术可以有效地提高成像质量，但不能完全消除温度变化对光学系统参数的影响。因此缺少对于基于几何光学参数温变模型的研究，目前该领域的研究仍然较少，缺少成熟的理论模型。

Podbreznik等人提出一种简单的模型，用于消除由特定温度条件引起的测量误差[7]。然而此模型是基于光学系统内参数及相机姿态不随温度变化的假设前提下，故该模型的应用范围和精度十分有限。Smith和Cope通过将镜头放置在恒温箱，取出后再进行安装标定的方法，研究了相机参数随温度的变化情况，但每次拆装过程中会不可避免的引起机械结构的改变。由于光学系统参数随温度变化的变化量本身就很小，因此无法确定其测量结果是否与拆装过程中机械结构改变有关，该测量方法不够严谨[8]。Handel研究了相机温度上升过程中，对图像处理的影响问题，并给出了相应的补偿方法。在该模型中，投影中心不变，且光学系统的内参数需保持不变。事实上，真实环境温度变化引起的热膨胀会改变光学系统的内参数，可见，此模型的假设也是不准确的[9，10]。姜广文团队通过半物理仿真和有限元分析相结合的方法研究了摄像测量中的温度效应及消除方法[11，12，13]。从以上文献分析中可以看出，目前对于光学系统参数随温度变化影响机理的研究还不够充分。

本文主要研究了相机内参数随温度变化的关系模型。首先介绍了相机的成像模型和实验设备。实验表明，温度变化会引起相机拍摄的图像点位置发生变化。同时，仿真证明了参数的变化会导致图像点位置发生变化。然后通过像点位置变化量和相机成像过程提出了图像点位置漂移模型。再通过曲线拟合方式得到了温度变化与内参数变化的关系模型。最后，验证了该模型能够有效地降低受温度影响的图像点位置漂移量，从而说明该模型可以减小温度对相机光学系统的影响。

2 相机模型和实验设备

2.1 相机模型

为了研究温度对相机光学系统内参数的影响，首先要研究相机成像原理[14]。相机成像的过程就是从三维空间转换到二维空间。针孔成像模型是理想的成像模型。由于本文研究的是温度变化对相机内参数的影响，因此在成像过程中选择针孔成像模型来实现从三维坐标系到二维坐标系的转换。假设现实世界中任意一点P的世界坐标系坐标为Pw(Xw，Yw，Zw)，该点相对应的相机坐标系中的坐标为Pc(Xc，Yc，Zc)，对应的像素坐标系中的坐标为p(u，v)。

1)世界坐标系到相机坐标系：这两个坐标系的变换属于刚体变换，只需要进行旋转和平移。其关系可表示为

Pc=RPw+t

(1)

2)相机坐标系到像素坐标系：相机坐标系中的任意点Pc(Xc，Yc，Zc)对应的像素坐标系中的投影点齐次坐标为p(u，v，1)，则这两点关系可表示为

Zcp=KPc

(2)

其中

(3)

K矩阵中这4个参数只和相机的内部结构有关。f为焦距，dx和dy分别是每个像素在图像平面x和y方向上的物理尺寸。u0和v0表示平移距离，与相机成像平面的大小相关。

2.2 实验设备

为了研究温度变化与光学系统参数变化的数学模型，必须通过实验的方法采集真实环境中温度变化与光学系统参数变化的数据集。

温控箱的箱体分为外侧固定支撑部分和内部保温层两部分。在镜筒表面覆盖导热材料，并在导热材料上粘贴多组半导体加热/制冷片以及温度传感器，温控系统通过分别控制多组半导体加热/制冷片的电流大小和方向模拟温度的快速变化，并通过温度传感器对温度变化进行实时监控，实现了对温变环境的模拟功能。箱体的正面留出镜头孔，外面再用圆形玻璃罩住，用胶水粘好，防止空气流动，光线又能透过玻璃进入镜头里面。箱体的侧面留出引线孔，方便信号线、控制线、半导体制冷片引线和温度传感器信号线的引出。实验设备如图1所示，主要分为三部分，其中图(a)为12×9棋盘格标定板，图(b)为实时显示当前镜筒温度的液晶显示屏，图(c)为控制镜头温度变化的温控箱。

图1 实验设备

采用半导体加热/制冷片可以快速实现温度变化，在面向内参数变化时，不仅控制精度更高，还能减少其它因素的影响。其中，镜头的型号为EB10210GDJ·HR，选自福建福光公司，半导体加热/制冷芯片采用TEC1-127，温度传感器选用DS18B20。在镜筒的四个方向都设置了温度传感器，为了短时间内可以快速对镜头控温，最后以平均温度作为基准。

3 温度影响与建模

3.1 温度对光学系统的影响

温度变化会导致光学系统不同组件的膨胀或收缩和光学材料折射率的变化，这些都会带来光学系统内参数的变化，从而影响相机的测量精度。

光学系统内参数受温度变化的影响可以通过实验直观体现为像平面中的点位置漂移现象，随机选取了在16℃和45℃时拍摄的标定板照片，并对中间80个像点数据做处理。如图2所示，其中图(a)为像点位置的整体漂移效果，可以看出来在不同的环境温度下，圆圈没有重合，也就是像点位置发生了变化，便于结果更突出显示，对图(a)选取部分点进行局部放大，如图(b)所示，明显看到圆圈位置发生漂移。说明像点位置会随着环境温度的变化而变化

图2 漂移现象

3.2 仿真验证

利用MATLAB对摄像机成像过程进行仿真，同样可以清楚地看到当内参数发生变化时，图像点的位置也会发生变化。如图3所示，其中图3(a)为主点u0和v0增加1/100倍后的效果，很明显可以看出，圆圈发生了漂移现象，没有重合；图3(b)为焦距f增加1/100倍后的效果，可以看出圆圈有向中间“聚拢”的现象。从这里也能看出来，内参数对像点位置的影响效果是不同的。由于光学系统参数受温度影响的变化量本身就很小，下图为坐标放大1000倍后的效果。

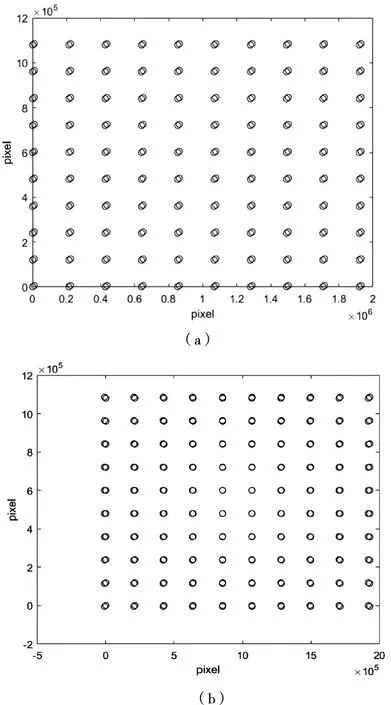
图3 仿真漂移现象

3.3 图像点漂移模型

温度变化是通过影响光学系统组件形变和材料折射率使得其内参数发生变化，进而影响光学系统性能。因为温度变化和图像点位置漂移量之间的关系是易得的，因此为了从理论上研究温度变化对光学系统内参数的影响，首先需要建立图像点坐标漂移量和参数变化量之间的关系模型，这样可以间接得到温度变化与内参数变化之间的模型关系。

以棋盘格中心点坐标建立世界坐标系，点Pw(Xw，Yw，Zw)为该坐标系中一点。设K′为温度变化后的内参数矩阵，对应的变化后的图像像素坐标系中的投影点的齐次坐标为p′(u′，v′，1)，模型建立过程如下：

首先将变化后的内参数矩阵K′和变化后的投影点坐标p′(u′，v′ )代入式(2)，得

Zcp^′=K′Pc

(4)

用δK表示内参数矩阵的变化量，像点坐标u和v的变化量分别用δu和δv表示，则

K′=K+δK

(5)

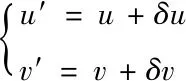
(6)

其中

(7)

将(5)-(7)代入(4)，得

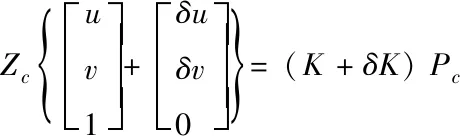
(8)

用式(8)减去式(2)得

(9)

将式(7)代入式(9)并展开得

(10)

用线性方程组形式来表示，得

(11)

上式中的i表示第i个点(i从1开始)。

其中

X=(δu0，δv0，δf/dx，δf/dy)T

(12)

通过求解上面的方程组即可得到图像点坐标漂移量和内参数变化量的关系，即图像点漂移模型。

3.4 温度变化和内参数变化的关系模型

通过上一节已经得到图像点坐标漂移量和参数变化量的关系，然后经过多组实验可以得到温度变化和像点位置漂移量的离散点对应关系，再借由漂移模型得到参数变化量，进而可以得到温度变化和内参数变化量之间的关系模型。下面采用曲线拟合方式来建立温度变化和内参数变化之间的关系模型。如式(13)所示

f(x)=a0+a1×cos(x×w)+b1×sin(x×w)+a2×cos(2×x×w)+b2×sin(2×x×w)

(13)

其中，输入为x表示温度的变化量，输出为f(x)表示内参数的变化量。a0、a1、a2、b1、b2、w是模型系数。从该模型可以得到温度变化与参数变化之间的关系。内参数随温度变化的拟合曲线如图4所示，(a)、(b)、(c)分别对应参数δu0、δv0δ、δf(dx和dy固定不变)。

图4 拟合曲线

4 模型验证

从上面可以看出，通过温度的变化量可以得到内参数的变化量，然后通过内参数的变化量又可以得到图像点的漂移量，为了验证该模型，进行了如下实验。

如图5所示:设置标准温度为20℃，随机选取其它温度下的图像点，其中“x”表示原始点集的漂移量，“.”表示经过模型修正后的点集漂移量。

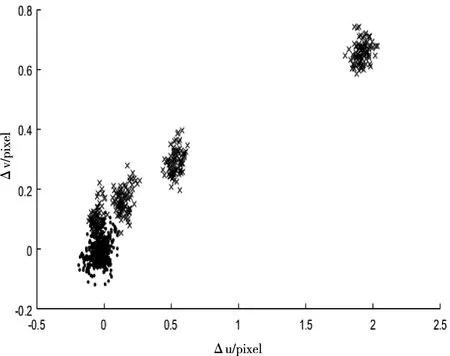
图5 模型验证

从上图中可以看出，原本分散的图像点集经模型修正后都集中在左下角。图像点集在x方向上的漂移量由大约2.5个像素下降到了0.3个像素左右，在y方向上的漂移量由大约0.7个像素下降到了0.3个像素左右。为了更直观地显示模型的修正效果，直接将温度差为20℃左右的两个点集漂移量进行比较，如图6所示。其中图(a)表示x方向的偏移量减小效果，图(b)表示y方向的偏移量减小效果。

图6 漂移量比较

从上图中可以看出，漂移量在x方向上从2个像素左右降低到0.3个像素左右，在y方向上的偏移量从大约0.7个像素左右降低到0.2个像素左右。该实验说明受温度变化影响的漂移量经过该模型修正后能够有效改善。

5 结论

温度变化会导致航天相机光学系统不同组件的膨胀或收缩和光学材料折射率的变化，这些都会带来光学系统内参数的变化，从而影响相机的测量精度。因此，对于温度变化影响的分析和修正是必不可少的。本文首先分析了温度变化对相机光学系统的影响机理，然后通过图像点漂移现象建立了图像点位置漂移模型，在此基础之上利用曲线拟合方式建立温度变化与内参数变化的关系模型，最后通过实验对该模型进行验证。结果表明，该模型可以有效地减小温度变化对相机测量的影响。