ADS-B信号交织概率仿真与分析

朱 栋，冯成涛，储开斌，宦 娟

(常州大学信息科学与工程学院，江苏 常州 213164)

1 引言

目前，空管系统中常用的监视技术主要有一次监视雷达(PSR)、二次监视雷达(SSR)、广播式自动相关监视(ADS-B)、场面监视雷达和多点定位(MLAT)[1-4]。在全球航行计划[5]和中国组块升级计划中[6]，在当前及未来相当长时期内，仍然会以上述几种监视技术为主要监视手段。

ADS-B是基于GPS全球卫星定位系统和空地、空空数据链通信的航空器运行监视系统。ADS-B系统通过飞行器主动发送自身相关信息的方式来实现地面或空中对目标的监视功能。国际民航组织(ICAO)将其确定为未来监视技术发展的主要方向，国际航空界正在积极推进ADS-B技术的应用。与传统二次雷达系统相比，ADS-B系统能够提供实时和准确的航空器位置、速度等信息，而且ADS-B系统具有建设投资小，维护费用低，使用寿命长等优点。ADS-B除了在空管监视中的重要应用之外，还能应用于雷达点迹的高精度标定[7，8]。1090扩展电文(1090ES)是实现ADS-B功能的三种数据链之一，其射频工作于1090 MHz，与二次雷达S模式应答信号的格式相同，ICAO重点推荐使用1090ES数据链。

随着航空运输业的迅猛发展，飞行器数量持续增加，由于二次雷达和1090ES等主要监视手段均使用1090 MHz这一频点，使得1090 MHz频点的同频干扰问题日益严重。同频干扰会使得ADS-B信号发生时域交织而无法被正确解码，进而造成航迹丢点。由于目标航迹连续性在空管监视中的重要性，研究ADS-B信号的交织概率，对于ADS-B地面站建设方案的设计具有非常重要的指导作用。当ADS-B信号交织概率过大时，应考虑采用多个扇区天线分空域接收信号，以降低信号交叠概率。

孙清清等[9]对1090 MHz频点的同频干扰的几种形式进行了总结，利用二项分布模型计算1090ES受A/C模式、S模式信号串扰的概率。刘萍等[10]研究了基于泊松分布的1090ES受干扰概率。胡来招等[11]研究了雷达信号侦察过程中不同雷达的脉冲信号相互交叠的概率，并对比了经典的泊松分布模型和祝正威等[12]提出的模型，并利用数值仿真的提出了修正的概率模型。1090ES信号交织概率属于离散随机事件问题，以上研究文献也基于离散随机事件的经典模型—泊松分布和二项分布模型展开分析，但未对模型中起决定作用的关键参数确定其数学表达式，也未利用两种数学模型进行相互印证。由于模型中的这些关键参数难以从数学上直接推导其表达式，本文通过仿真找出确定这些参数的表达式，并利用两个模型互相印证参数表达式的正确性，从而得到估计ADS-B信号交织概率的具体算法。

2 仿真方法

工作在1090 MHz频点上的主要信号有二次雷达模式A/C的应答信号、ADS-B的1090ES-112bit长格式信号和1090ES-56bit短格式信号。由于具备模式S询问功能的二次雷达数量较少，所以暂时不考虑模式S的应答信号。模式A/C的应答信号只有在地面二次雷达询问时目标才会被动发射，因此，模式A/C应答信号的个数与地面二次雷达的部数、二次雷达帧扫描周期以及询问周期有关，而ADS-B信号则是目标主动发射，其发射周期遵循航空无线电规范。

仿真中，假定在1秒时间段内，模式A/C的应答信号、1090ES-112bit信号和1090ES-56bit信号到达某ADS-B地面站的时间由matlab的rand函数随机产生。1秒时间段内，1090ES信号的总个数根据目标数和航空无线电规范约定的发射频率(每个目标发射1090ES-112bit信号5.2次/秒、1090ES-56bit信号1次/秒)而定，模式A/C的应答信号的总个数则由目标数、二次雷达部数及二次雷达的询问周期和帧扫描周期等参数确定。每个模式A/C的应答信号、1090ES-112bit信号和1090ES-56bit信号的时长确定，分别为20.75 μs、120 μs和64 μs。在时间轴上，根据随机产生的每个信号的到达时间和各种信号的持续时间，即可判断信号是否发生交织。仿真中，仅统计1090ES-112bit信号发生交织的个数，而不关注1090ES-56it信号，因为目标的位置、速度、航向等重要信息调制在1090ES-112bit信号上。

上述仿真重复多次，累计1090ES-112bit信号发生交织的个数，求取平均值即可得到在某特定情况下(特定的目标数、二次雷达部数、二次雷达帧扫描周期和二次雷达询问周期)，在1秒时间段内，总共发生交织的1090ES-112bit信号个数。将此交织的1090ES-112bit信号个数除以1秒时间段内所有的1090ES-112bit信号个数即可得到总交织概率。总交织概率将遵循泊松分布和二项分布模型，两种模型的表达式分别如下式(1)和(2)所示

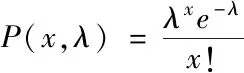
(1)

其中，x为交织次数，λ为平均交织次数。

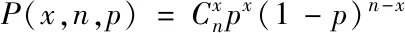
(2)

其中，x为交织次数，n为信号个数，p为单个信号交织发生概率。当p值较小时，上述两个模型等效，且λ=np。

另外，单个1090ES-112bit信号时长较长，单个1090ES-112bit信号可能发生1次、2次、…、m次交织，仿真中可分别统计并计算发生1次、2次、…、m次交织的概率，这些交织次数独立的交织概率的总和就是总交织概率。总交织概率可通过令泊松分布模型中x=0，利用下式(3)获得

P=1-P(0，λ)=1-e-λ

(3)

3 仿真结果分析

3.1 总交织概率与交织次数独立的交织概率

根据航空无线电规范，每个目标每秒主动发射1090ES-112bit信号5.2次，每秒主动发射1090ES-56bit信号1次。假定某区域内有二次雷达4部；每部雷达扫过某个目标时引发目标模式A/C的应答，假定每部二次雷达平均每秒引发某个目标5次模式A/C的应答。目标数从50批变化到1000批，利用上述仿真方法，得到不同目标数时的总交织概率、发生1次交织的概率、发生2次交织的概率、发生3次交织的概率和发生4次交织的概率，如下图1所示。随着目标数增加，单个1090ES-112bit信号发生多次交织的概率逐渐增大。

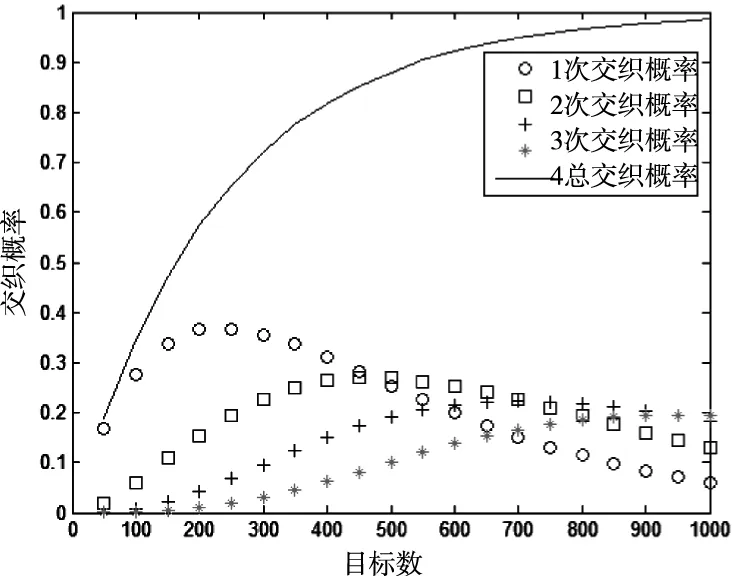
图1 总交织概率(实线)与交织次数独立的交织概率(1次-圆圈、2次-方框、3次-加号、4次-星号)

之所以分不同的交织次数来讨论交织概率，是因为1次交织的情况相对简单，仍然有可能通过时域波形上特征分离交织信号[13-15]。当排除1次交织的情况后，难以实现分离的多次交织的概率总和也将下降。如果未来1次交织信号的分离技术逐步成熟，信号交织概率的容忍度就将得以提升。

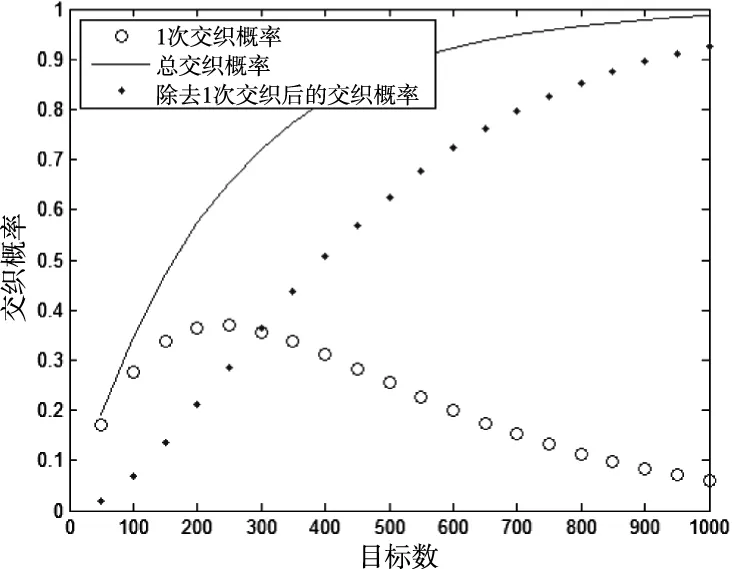
图2 总交织概率(实线)、1次交织概率(圆圈)与除去1次交织后的交织概率(点)

根据图1中的总交织概率并利用式(3)，可以计算出泊松分布模型的平均交织次数λ。再根据p=λ/n，以及二项分布模型式(2)，也可计算出1次、2次、…、m次的交织概率，其中n为1090ES-112bit信号的个数。将此计算出的交织次数独立的交织概率与直接仿真得到的结果进行对比，如图3所示，两者完全吻合，说明仿真方法与结果的正确性。

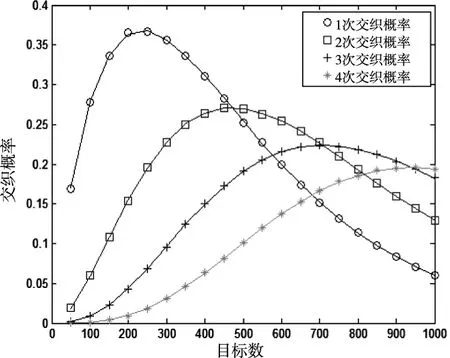
图3 交织次数独立的交织概率(实线为理论计算结果、标号为图1中仿真结果)

3.2 平均交织次数与单个信号发生交织概率

保持二次雷达的工作参数，而使二次雷达的部数从0变化到4，目标数仍从50批变化到1000批，可得如图4所示不同雷达部数时的总交织概率仿真结果以及由总交织概率推算出来的平均交织次数λ和单个信号发生交织概率p。

图4 交织概率

由图4(a)可知，随着二次雷达部数减少，模式A/C应答信号数量随着减少，1090ES-112bit信号发生交织的概率也整体下降；由图4(b)仿真结果表明，随着目标数的增加，1090ES-112bit信号个数增加，平均交织次数也随之线性增大，其比例系数定义为

kλ=λ/N

(4)

其中N为目标数；由图4(c)可知，单个信号发生交织概率p与目标数无关，而仅与二次雷达部数有关。二次雷达的部数直接关系到单个目标一秒内发射信号的总时长kD，其定义如下：

kD=f112t112+f56t56+NssrfACtAC

(5)

其中，f112和f56分别为平均每秒每个目标的发射1090ES-112bit和1090ES-56bit信号的次数；t112和t56分别为单个1090ES-112bit信号时长(120μs)和1090ES-56bit信号时长(64μs)；NSSR为二次雷达部数；fAC为对应二次雷达平均每秒引发每个目标模式A/C的应答次数；tAC为单个模式A/C应答信号时长(20.75μs)。式(5)中，可变量仅有NSSR和fAC。

3.3 交织概率估计算法

将二次雷达部数分别设定为0、1、2、3、4，fAC分别设定为4、5、6、7。将不同NSSR和fAC组合时的(kD，kλ)结果绘于图5。每组fAC的结果从左下至右上分别对应二次雷达部数从小到大。

由图5可知，无论NSSR和fAC如何变化，kD和kλ呈直线关系，直线方程为

kλ=6.786kD-0.00324

(6)

图5 不同NSSR和fAC时的kD和kλ的直线关系，其中，kD为横轴，kλ为纵轴

其中，系数6.786≈(t112+tAC)/tAC，这是由于1090ES-112bit大多与模式A/C的应答信号交织。因此，根据仿真结果得出的式(4)和(6)就可以直接计算出泊松分布模型中平均交织次数λ为

λ=(6.786kD-0.00324)N

(7)

其中，N为目标数，单个目标一秒内发射信号的总时长kD根据式(5)直接计算。并且，二项分布模型中的单个信号交织发生概率p为

p=(6.786kD-0.00324)N/n

=(6.786kD-0.00324)/f112

(8)

其中，n为1090ES-112bit信号个数。式(8)表明p与目标数N无关，仅与kD和f112相关。当fAC为5，NSSR=0、1、2、3、4时，根据式(8)可计算得出p的值示于下表1中。表1中p的结果与图4(c)中仿真所得结果完全吻合，证明了式(8)的正确性。而文献[9]仅简单的将t112与tAC之和作为p值，并未考虑kD对p的影响。

表1 当fAC为5时，根据式(8)推算得到的p值

4 结论

随着民航飞行器的持续增加，ADS-B信号与二次雷达应答信号的同频交织问题日益严重。ADS-B信号交织将使得目标航迹丢点，影响空中管制系统对目标的持续跟踪。ADS-B信号交织概率是ADS-B地面站建设方案设计需参考的重要指标之一。ADS-B信号交织属于离散随机事件问题，可以参照经典的泊松分布模型和二项分布模型进行估计。截止目前的文献虽以这两种模型展开了研究，但未明确模型中起关键作用的参数的给定方法。本文首先通过仿真得到了总交织概率和交织次数独立的交织概率的数值解，并验证了泊松分布与二项分布的内在关联；其次，改变仿真条件中的目标数和二次雷达部数对交织概率进行仿真，得到了与目标数呈线性关系的平均交织次数和与二次雷达部数相关的单个信号平均交织概率的数值解；再次，通过改变二次雷达部数和A/C模式应答频数的仿真，得到平均交织次数比例系数与单个目标单位时间内信号总时长之间的线性关系，从而得到计算平均交织次数的数学表达式；最后，通过平均交织次数与单个信号平均交织概率的内在关联，推导出单个信号平均交织概率的表达式，其理论计算结果与仿真结果完全吻合，从而证明了ADS-B信号交织概率估计算法的正确性。