拓扑与资源感知的虚拟网络功能迁移方法
2021-11-17孟相如康巧燕韩晓阳
阳 勇,孟相如,康巧燕,韩晓阳
空军工程大学 信息与导航学院,西安710077
随着互联网技术的飞速发展,网络应用更新换代速度加剧。而传统网络中网络功能大都基于专有硬件,部署和升级都要对硬件设施进行更改,一定程度上增加了运营商的开销[1]。网络功能虚拟化(network function virtualization,NFV)是下一代网络重要技术之一,通过解耦硬件设备与运行于其上的网络功能,实现网络功能的灵活部署、动态扩展以及软硬件的发展周期分离[2]。利用NFV 技术,网络功能可以当成一个普通软件的实例,部署和升级过程不需要重新购置和安装新的硬件,从而降低运营商的运营成本[3-4]。
在NFV 环境的网络中,由于服务功能链(service function chain,SFC)请求的到达时间与生存周期的差异性,随着时间的推移,部分物理节点将部署大量虚拟网络功能(virtual network function,VNF),其资源占用率达到瓶颈后,服务质量(quality of service,QoS)急剧下降[5]。与此同时,网络中存在只部署少量VNF 的节点,其大量资源处于空闲状态。若能将部署于负载较重节点上的VNF 迁移到负载较轻的节点上,实现物理网络的负载均衡[6],则能在充分利用底层网络资源的同时提高QoS。
目前针对NFV 环境中网络的负载均衡问题已有相关研究[7-15]。文献[7-9]研究了面向负载均衡的VNF部署问题,其中文献[7]提出一种基于深度强化学习的双深度Q 网络VNF 部署算法,使用机器学习收集网络的流量信息并计算资源占用阈值,按照基于阈值的策略部署VNF。文献[8]以负载均衡与链路时延为原则,采用Google 对网页排名的PageRank 算法进行节点评价,将VNF 部署在综合能力最大的节点上。文献[9]研究了具有布局约束的VNF 部署,每次贪婪地将下一个VNF 部署到当前负载最低且满足位置约束的服务器上。这类方法在VNF 部署完毕的初期对网络有较好的负载均衡性能,但难以避免随着时间的推移依然出现负载失衡问题。文献[10-12]研究了有关负载均衡的VNF 迁移,其中文献[10]提出一种多优先级的VNF 迁移开销与网络能耗联合优化算法,针对节点资源使用情况划分了5 个分区,基于贪心算法对其采取不同的迁移策略,低过载节点进行VNF合并,高过载节点进行负载均衡。该算法能在降低网络能耗的同时提高负载均衡程度,但分区太多加大了算法的复杂程度。文献[11]提出一种基于多维环境感知的VNF 快速自适应迁移算法,采用固定阈值的资源感知算法选择待迁移VNF,利用TOPSIS 算法对节点进行评价并选择迁移目的节点,能保证迁移开销的基础上,提升底层网络的负载均衡程度,但未考虑迁移后收益开销比问题。文献[12]提出一种优化网络影响的VNF 迁移方法,以降低SFC 时延为目标,同时兼顾节点负载与迁移成本,有效提高了SFC 的时效性,但对网络的负载均衡提升不明显。文献[13]提出使用虚拟软件定义网络(software defined network,SDN)控制器作为VNF 来实现负载均衡的方法,当底层网络负载失衡并且流量持续增加时,添加一个辅助的虚拟SDN 控制器共享高负载节点的负载,有效降低了高负载节点资源占用率,但添加SDN控制器加重了运营商的开销。文献[14]面向负载均衡对VNF 迁移方法进行了一般步骤的介绍。文献[15]设计了一种面向NFV 的高性能四层网络负载均衡机制,但二者均未给出关于负载均衡的具体方法。
针对上述问题,本文提出一种拓扑与资源感知的VNF 迁移方法(topology and resource-aware virtual network function migration method,TRA-VNFM)实现网络的负载均衡。首先通过两级动态阈值判定算法优先对高过载节点实施VNF 迁移,同时计算出待迁移目的节点集。然后采用资源感知算法计算部署于过载节点上的VNF 的迁移权重,并结合资源需求确定待迁移VNF。最后通过极值交互的拓扑感知算法综合考虑物理节点的各类属性,选择出最适合迁移的目的节点。实验表明,本文提出的TRA-VNFM 方法在降低SFC 的平均时延和提高网络收益开销比的基础上,对网络的负载均衡程度有较大提升。本文的主要贡献有:
(1)设计两级动态阈值判定VNF 是否进行迁移,有效提高了网络的负载均衡程度。
(2)提出节点就近契合度作为拓扑感知的评价指标,降低了SFC 端到端的平均时延。
(3)将极值交互式多目标决策方法运用于节点评价中,综合考虑了各评价指标与其组成的整体对结果的影响,提升了VNF 迁移方法的性能。
1 网络模型及评价指标
1.1 网络模型
物理网络由加权无向图G=(N,E)表示,N是物理节点集合,E是物理链路集合。任意节点ns∈N,拥有的资源由三元组表示。其中表示计算资源,表示存储资源,表示转发资源。ns的处理速度为proc(ns)。任意一条链路es∈E,其带宽为b(es),时延为d(es)。
m条虚拟SFC 组成的集合为F=(f1,f2,…,fm),fi表示第i条虚拟SFC,可用六元组(Ii,Oi,Di,Si,Vi,Li)表示,Ii为源端点,Oi为目的端点,Di为最大允许时延,Si为数据包大小,Vi为VNF 集合,Li为虚拟链路集合。其中Vi=(vi,1,vi,2,…,vi,n),vi,j表示fi的第j个VNF,其资源需求用三元组表示,表示计算资源需求,表示存储资源需求,表示转发资源需求。Li=(li,0,li,1,…,li,n),li,0表示Ii到vi,1之间的虚拟链路,li,n表示vi,n到Oi之间的虚拟链路,当j≠0,n时,li,j表示vi,j到vi,j+1之间的虚拟链路。Ti,j表示li,j的带宽需求。



Table 1 Meaning of major variables表1 主要变量含义
1.2 节点评价指标
(1)节点ns的k类资源占用率ηk(ns) 。设k∈(cal,mem,for),分别表示计算、存储、转发,对于任意物理节点ns∈N,其k类资源占用率ηk(ns)定义为当前部署(包括迁入)于ns的VNF 对k类资源的占用量与ns所拥有的k类资源总量的比值,其计算公式为式(1)。
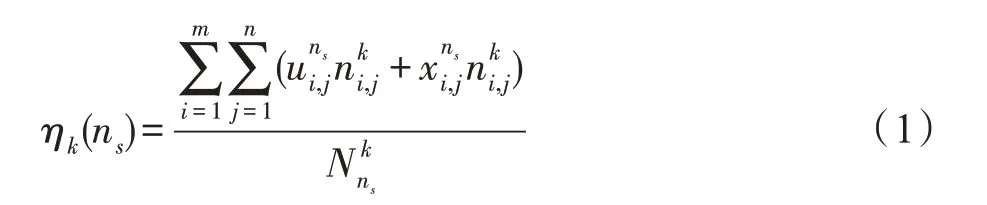
(2)节点ns对部署于其上的vi,j的处理时延本文采用通用处理器共享算法下的处理时延模型[11],如式(2)所示。

式中,tproc表示vi,j对数据包的处理时间,其计算方式为tproc=Si/proc(ns)。loadns表示节点ns上处理器负载百分比,即为计算资源占用率ηcal(ns)。loadi表示vi,j的计算资源需求与节点ns上所占计算资源的比值,即上下同比并令得的物理意义为部署于节点ns上的vi,j对ns计算资源的占用率。因此节点ns对vi,j的处理时延计算公式转化为式(3)。

(3)节点nr的就近契合度。其表示vi,j迁移的目的节点nr与待迁移fi之间的紧密程度,计算公式设计为式(4)。

式中,ns为迁移的出发节点,nr为迁移的目的节点,为待迁移vi,j所在fi中vi,j+1所部署的物理节点,为待迁移vi,j所在fi中vi,j-1所部署的物理节点。若待迁移vi,j为所在fi中第一个VNF,则n-s为源端点,若待迁移vi,j为所在fi中最后一个VNF,则n+s为目的端点。为节点nr与节点之间的最短跳数,同理。TD(nr)为节点nr的邻接节点数目。就近契合度越大,迁移的目的节点nr与fi在物理拓扑上联系越紧密,反之越松弛。节点就近契合度可作为VNF 迁移时进行拓扑感知的评价指标。
1.3 方法评价指标
(1)负载均衡指数α,用来衡量网络负载均衡的效果,其计算公式设计为式(5)。

(2)收益开销比γ,计算公式为式(6):
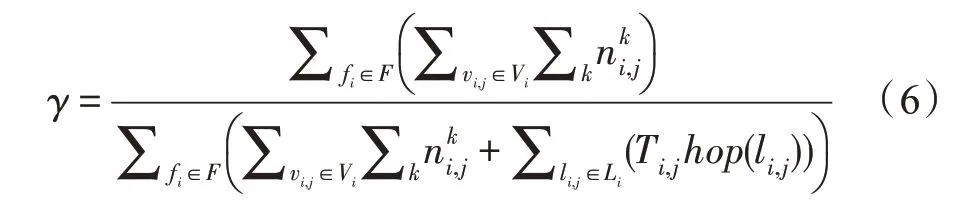
式中,hop(li,j)表示li,j部署到底层网络后的跳数。收益开销比γ越大的网络性能越好。
(3)虚拟SFC的平均时延delay,计算公式为式(7)。

式中,delayi表示fi的时延,|F|表示集合F中元素的个数,即SFC 条数。在计算delayi时既要考虑节点的处理延时,还要考虑链路的传输延时d(es),因此delayi的计算公式为式(8):
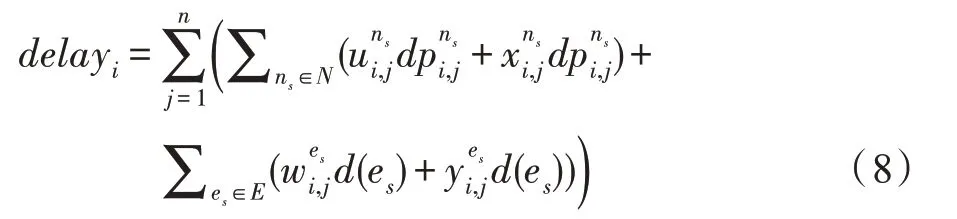
虚拟SFC 平均时延delay越小的网络性能越好。
2 VNF 迁移方法
2.1 基于两级动态阈值的迁移判定算法
为确定触发VNF 迁移的条件,需要对物理节点设置资源过载阈值;为使迁移尽量对高过载节点进行,并提升高过载节点的迁移成功率,需要对节点的过载程度进行分级,并对不同级别的过载节点设置不同的迁移判定条件;为使VNF 迁移更适应当前网络环境,过载阈值应随网络的负载变化而动态变化。基于此原则,本文针对物理节点的k类资源占用率,设置两级动态阈值,其中,针对N中的物理节点ns:
若ns存在某种资源占用率,则称之为二级过载节点。若ns不是二级过载节点,但存在ηk(ns)>则称之为一级过载节点。ns的迁移具体判定过程如图1 所示。
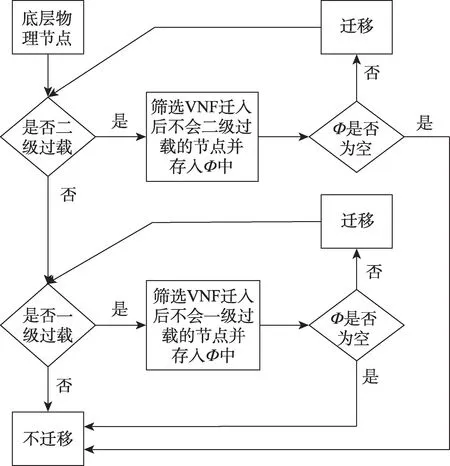
Fig.1 Migration judgment process based on two-level dynamic threshold图1 基于两级动态阈值的迁移判定过程
首先判断ns是否为二级过载节点。若是,则计算其待迁移目的节点集合Φ是否为空。对于二级过载节点,Φ定义为将待迁移VNF 迁入后仍然不会二级过载的节点集合。若Φ不为空,则在Φ中选择节点作为迁移的目的节点并实施VNF 迁移,直到ns不再二级过载。若Φ为空,则说明网络中各节点都负载严重,无法再对ns进行负载均衡,故不进行VNF迁移。
若ns不是二级过载节点,或经过VNF 迁移后已从二级过载节点中移除,则判断其是否为一级过载节点。若是,则计算其待迁移目的节点集合Φ是否为空。对于一级过载节点,Φ定义为将待迁移VNF迁入后仍然不会一级过载的节点集合。若Φ不为空,则在Φ中选择节点作为迁移的目的节点并实施VNF 迁移,直到ns不再一级过载。若Φ为空,则说明此时底层网络的负载已较为均衡,无需进行迁移。
为实现过载阈值随网络的负载变化而动态变化,k类资源的一级过载阈值设定为物理网络中该类资源的均值,即为式(9):

式中,|N|表示物理节点集合N中元素的个数,即物理节点总个数。k类资源的二级过载阈值设定为该类资源的一级过载阈值与1 的均值,即为式(10):

2.2 基于资源感知的待迁移VNF 选择算法
一个过载的物理节点上可能部署了多个VNF,需要从中选择待迁移VNF。引入迁移指数θi,j(ns)表示节点ns上的vi,j适合迁移的程度。本算法基于资源感知的动态权值计算迁移指数,保证二级过载资源的权重大于一级过载资源,一级过载资源的权重大于不过载资源,占用大过载级别资源越多的VNF迁移指数越大。
令l∈{1,2},则k类资源l级过载阈值可表示为定义表示节点ns的k类资源是否l级过载,即ηk(ns)是否大于。则迁移指数计算公式设计为式(11)。


通过比较过载节点上各VNF 的迁移指数大小,值最大的VNF 进行迁移,若节点仍然过载,则将剩下的VNF 中值最大的继续进行迁移,直到节点不再过载。
2.3 基于拓扑感知的目的节点选择算法
在集合Φ中进行目的节点选择是一个多目标决策问题,本文通过极值交互的拓扑感知算法对Φ中节点进行评价并计算迁入指数。其中拓扑感知通过使用评价指标实现,迁入指数用来衡量节点作为迁移目的节点的适合程度。最终选择迁入指数最大的节点作为迁移目的节点。极值交互的拓扑感知算法中节点评价与迁入指数计算过程如下:
步骤1确定评价指标。本文对待迁移目的节点nr的评价指标有计算资源占用率ηcal(nr),存储资源占用率ηmem(nr),转发资源占用率ηfor(nr),对待迁移vi,j的处理时延就近契合度,其中ns为迁移的出发节点。越小,越大,则节点nr的迁入指数越大。令集合φ=
步骤2计算待迁移目的节点nr的各项评价指标满意度ρ。评价指标满意度反映节点nr的某项评价指标与所有待迁移目的节点中该项评价指标最优值的契合程度,其计算方法如式(13)、式(14)所示,其中a代指ηcal(nr)、ηmem(nr)、ηfor(nr)以及中任意一个评价指标。

步骤3计算待迁移目的节点nr的总体协调度λ(d)。总体协调度反映节点的各项评价指标总体与理论最优节点之间的契合程度,其与各项评价指标满意度结合完成对迁移目的节点的选择。总体协调度计算方法如下:
首先计算节点的各项评价指标与其相应最优值之间的欧式距离和d1,如式(15)所示。

然后计算各项评价指标最优值与最差值之间的欧式距离和d2,如式(16)所示。
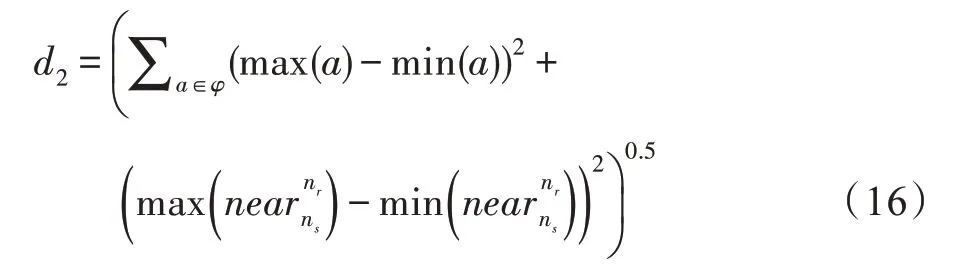
最后结合d1、d2构造总体协调度λ(d),计算方法如式(17)所示。

步骤4计算待迁移目的节点nr的迁入指数τ(nr)。设总体协调度允许的下限值为λ(d-),集合φ中各项评价指标满意度允许的下限值分别为ρ(a-),的满意度允许的下限值为若某项评价指标满意度低于其下限值,则计算出下限值与其的差值,定义为该项评价指标的补差值。若评价指标满意度高于或等于其下限值,则补差值为0。总体协调度的补差值亦然。补差值的引入可以增加低于下限值的评价指标满意度对节点迁入指数的影响。设总体协调度的补差值为z*,满意度的补差值分别为z1、z2、z3、z4、z5。则待迁移目的节点nr的迁入指数计算公式为式(18):

待迁移目的节点nr的迁入指数τ(nr)随各项评价指标满意度与总体协调度的增大而增大,随其补差值的增大而减少,反映了nr作为迁移目的节点的适合程度。因此在VNF 迁移中,选择τ最大的节点作为VNF 迁入的目的节点。VNF 迁移成功后,再对相关联虚拟链路进行重新部署。先将不满足虚拟链路带宽需求的物理链路删除,然后在剩余物理网络拓扑中运行k-最短路径算法重新部署虚拟链路。
综合以上三种算法,拓扑与资源感知的VNF 迁移方法基本流程如下所示。


3 实验仿真
本文通过Matlab 进行两组仿真实验对比TRAVNFM 方法与其他三种VNF 迁移方法的性能。第一组实验通过比较单次迁移平均时间和总迁移时间,对比四种方法在迁移过程中的性能。第二组实验通过比较负载均衡指数、收益开销比和SFC 平均时延,对比四种方法在迁移后对网络的优化程度。
3.1 仿真环境设置
物理网络是一张有25 个节点和27 条链路的连通图,为提高系统的稳定性,从中设置5 个节点空闲。实验各项参数如表2 所示。其中满意度下限与协调度下限通过多次调试,最终确定为效果最优的表中所示值。
3.2 不同方法对比
本文将TRA-VNFM 方法与其他三种VNF 迁移方法在相同实验环境下进行对比,如表3 所示。
3.3 算法性能分析
迁移过程中计算、存储与转发资源的一级与二级过载阈值如表4 所示。
为适应物理网络整体的资源占用变化,每一种资源的过载阈值都随着SFC 数量的变化而动态调整。随着SFC 数量的增加,网络整体负载上升,过载阈值随之上升。同时每种资源的二级过载阈值都高于其一级过载阈值,这是为了实现迁移优先对高过载节点进行,并提升高过载节点的迁移成功率。

Table 2 Simulation parameters表2 仿真参数

Table 3 Comparison of different VNF migration methods表3 不同VNF 迁移方法对比
第一组实验结果如图2 和图3 所示。
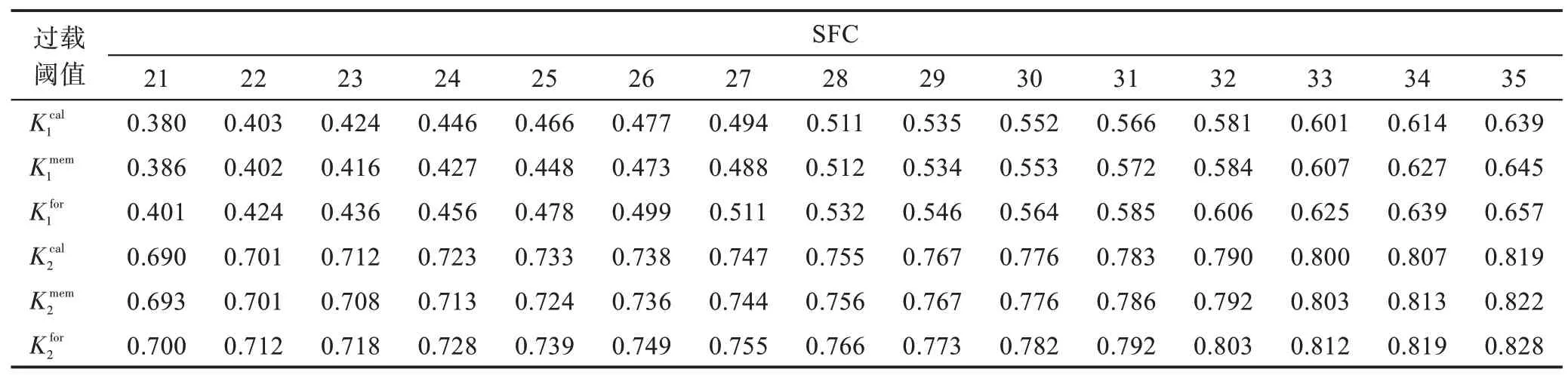
Table 4 Variation of overload threshold表4 过载阈值变化情况

Fig.2 Average time for single migration图2 单次迁移平均时间

Fig.3 Total migration time图3 总迁移时间
图2 是四种方法的单次迁移平均时间随服务功能链请求增加的变化对比图,从图中可以发现TRAVNFM 与OTRA-VNFM 单次迁移的平均时间小于MJOVME-VNFM 与RT-VNFM。这是因为TRAVNFM 与OTRA-VNFM 在对迁移目的节点选择时进行了拓扑感知,选择了与待迁移SFC 较近的节点作为迁移的目的节点,从而降低了单次迁移的时间。在TRA-VNFM 与OTRA-VNFM 的对比中,由于两者分别采用二级阈值和一级阈值进行迁移判定,迁移次数和迁移目的节点具有差异性,导致二者的单次迁移平均时间有所不同。
图3 是四种方法的总迁移时间随服务功能链请求增加的变化对比图,TRA-VNFM 与OTRA-VNFM的总迁移时间略小于MJOVME-VNFM 与RT-VNFM。这是因为TRA-VNFM 与OTRA-VNFM 在目的节点选择过程中增加了节点就近契合度作为评价指标,与MJOVME-VNFM 和RT-VNFM 只考虑资源占用率相比,TRA-VNFM 与OTRA-VNFM 虽减小了单次迁移的平均时间,一定程度上也增加了迁移次数。但TRA-VNFM 与OTRA-VNFM 采用极值交互的多目标决策算法对迁移目的节点进行选择,既考虑各评价指标的影响,又考虑其组成的整体产生的影响,因此在总迁移时间方面仍然具有优势。
第二组实验结果如图4~图6 所示。

Fig.4 Load balancing index图4 负载均衡指数

Fig.5 Revenue to expense ratio图5 收益开销比

Fig.6 Average delay of SFC图6 SFC 平均时延
图4 是四种方法的负载均衡指数对比图,TRAVNFM 的负载均衡效果明显优于另外三种方法。这是因为TRA-VNFM 使用了两级动态阈值迁移判定条件,相对于后三种方法,TRA-VNFM 优先对高负载节点进行迁移,并提升了高负载节点的迁移成功率。而高负载节点的减少会明显降低节点资源占用率方差,从而使得网络的负载均衡指数增加。
图5 比较了四种方法的收益开销比,TRA-VNFM与OTRA-VNFM 相较MJOVME-VNFM 与RT-VNFM得到了更高的收益开销比。这是因为进行了拓扑感知的TRA-VNFM 与OTRA-VNFM 在对目的节点进行评价时选择了与SFC 原部署路径紧密的节点作为迁移的目的节点,使迁移后SFC 的物理长度相较于MJOVME-VNFM 和RT-VNFM 更小,从而具有更小的链路开销,更高的收益开销比。
图6 是四种方法的SFC 平均时延对比图,SFC 的平均时延受到迁移目的节点的处理时延和重构链路的传输时延影响。而TRA-VNFM 与OTRA-VNFM在进行节点评价时,既将节点时延作为评价指标,使迁移目的节点的处理时延尽可能小,又通过就近契合度,使迁移后SFC 的物理长度尽可能小。因此与MJOVME-VNFM 和RT-VNFM 相比,TRA-VNFM 与OTRA-VNFM 具有更低的SFC 平均时延。
4 结束语
本文基于NFV 环境中网络负载均衡的特点,提出一种拓扑与资源感知的VNF 迁移方法。首先,设置两级动态阈值及相应的迁移判定条件,优先对高负载节点进行迁移。其次,使用资源感知算法计算待迁移节点上各VNF 适合迁移的程度,优先迁移对高过载资源占用多的VNF。最后,利用极值交互的拓扑感知算法对待迁移目的节点进行评价,完成迁移目的节点的选择。实验表明,本文提出的TRA-VNFM方法在降低SFC 的平均时延和提高网络收益开销比的基础上,对网络的负载均衡程度有较大提升。下一步将对SFC 的生存性进行研究,进一步提高NFV环境中网络的性能。
