基于多尺度卷积神经网络的高光谱图像分类
2021-11-17尤洪峰
刘 娜,宋 娟,董 丽,尤洪峰
(1. 青岛黄海学院智能制造学院,山东青岛 266427;2. 新疆大学 信息科学与工程学院,新疆乌鲁木齐 830000)
1 引言
高光谱图像(HSIs)在每个像素中包含数百个波段。由于高光谱图像光谱的丰富性,它们被广泛用于农业[1]、林业[2]和城市分区等[3]。丰富的波段给HSIs图像带来了足够的特征的同时也产生了许多冗余特征。最近,研究人员提出了一些新的方法来解决冗余特征。聂飞平[9]等提出了一种特征自动加权模型,使得冗余特征最小化。Ayinde等人[10]通过为不同的冗余特征建立相对余弦距离,最终消除了大量冗余特征并降低了模型计算成本。主成分分析(PCA)在消除冗余特征方面起着重要作用[11-14],并且它不受参数设置的影响,所以选择了PCA模型做特征预处理。小样本HSIs也是特征挖掘和分类中的一个难题。为了更好地实现高光谱图像的小样本分类,研究者们做了大量的研究,如支持向量机(SVM)[4],条件随机场(CRF)[5],k最近邻(KNN)[15],基于聚类[16]等。然而,上述方法对挖掘高维特征不够充分。近年来,深度学习由于其强大的特征学习和分类能力,在图像分类方面取得了越来越大的成就[17]。为了更好地挖掘高维特征,Mesut Salman[6]等人使用AlexNet提取高光谱图像的形态特征,并通过形态特征来加强特征间的空间关系;Mercedes E.Paoletti等人[7]提出了一种残差神经网络(ResNet),逐步增加卷积维数,最终实现冗余特征的消除。Gefei Yang 等人[8]提出了一种双通道稠密卷积网络(DenseNet)来提取高光谱图像的光谱特征和空间特征,并通过充分利用多种特征进一步提高了图像分类的精度。以上方法在特征挖掘中表现出优异的性能。
然而,由于卷积核的大小决定了最终学习的特征,且高光谱图像具有高维特征的性质,使得单个卷积核难以适用。虽然深层网络可以通过挖掘更深的特征来获取更多的信息,但随着模型层数量的增加,大量的有用特征同样被丢失。最终导致复杂的小样本高光谱图像识别变得困难。H Lee[18]等人提出了上下文CNN挖掘不同尺度的高光谱图像特征,并取得了良好的效果,但这方面的工作只是对输入部分进行了改进,模型的中后期对特征的挖掘还不够全面。为了解决上述问题,提出了一种MSC运算方法,在整个网络中同时对每个模块提取不同尺度的卷积特征。实验结果表明,该算法能较好地挖掘高光谱图像的特征。这篇文章的主要贡献如下:1)首次将MSC方法应用于任意模型中的每个卷积模块。这种方法特别适用于样本有限的小规模数据集。2)为了更好地理解MSC卷积的训练结果,对三个公共数据集进行了收敛性可视化分析。
2 模型结构
图1显示了基于AlexNet算法提出的MSC运算方法。首先,利用PCA算法对原始高光谱图像进行降维,保留其大部分信息维数,降低了计算量。其次,将降维后的特征输入改进后的AlexNet模型,最后通过Softmax预测每个像素并实现识别。
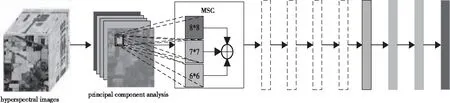
图1 改进后的AlexNet模型
图1中,MSC代表提议的MSC,虚线表示MSC方法,绿色矩阵表示Maxpooling层,蓝色矩阵表示密集层,紫色矩阵表示Softmax函数,⊕表示特征融合操作。
2.1 传统卷积
卷积可以根据给定的权重自动计算特征,最终保留有用的信息(如图像方向边、线、点等)。局部信息通过Flatten 层组合得到图像的全局信息。每个卷积核对应于一个基本特征,并且生成一对特征映射,并且共享特征图中的权重。传统的卷积运算如图2所示。

图2 传统的卷积运算过程
图2 中,绿色矩阵表示输入特征,橙色矩阵表示3的卷积核,粉红色矩阵表示输出。
传统的卷积公式如下所示
i,j代表了图像输入特征点的横坐标和纵坐标;n代表了卷积运算的次数;X代表了图像特征矩阵;Wk代表了卷积核为k的权重矩阵;bk代表了卷积核为k的偏置函数;S表示得到的新特征矩阵;*表示卷积运算公式。
2.2 多尺度卷积
特征挖掘直接受卷积核尺度的影响。有时单个卷积核不能充分挖掘复杂图像中的关键特征,导致一些关键特征的丢失。为了解决上述问题,提出了一种新的MSC方法,通过多个卷积核利用多个尺度同时挖掘特征。实验结果表明,MSC能更多的保留关键特征。MSC运算如图3所示。
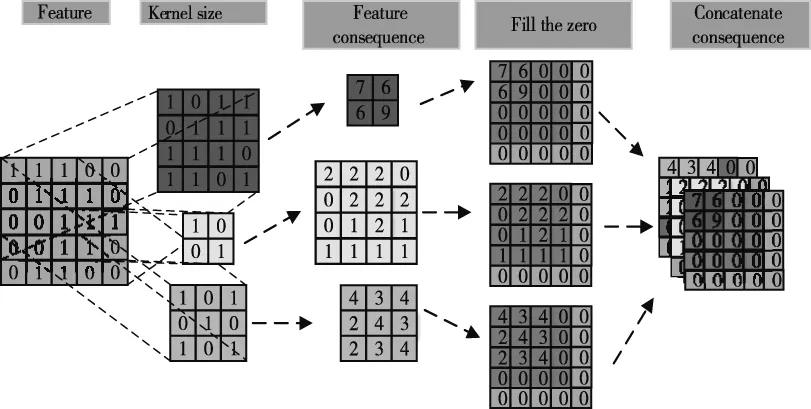
图3 MSC运算过程
图3中,绿色表示输入特征;红色、橙色和黄色表示不同尺度下卷积核的大小,粉色表示各卷积核运算结果;多颜色矩阵表示输出的特征结果;多尺度特征通过级联融合作为下一模块的输入。
多尺度卷积公式如下所示:
W(k-1,k,k+2)代表了k-1,k,k+1 三个不同尺度的卷积核运算;b(k-1,k,k+1)分别代表了k-1,k,k+1 三个卷积的偏执函数。
2.3 特征融合与分类
首先提取包含丰富空间信息和光谱信息的三维特征矩阵D(x,y,b),然后利用PCA算法进行降维,保留其包含重要特征的维数。最后,将降维的3-D特征矩阵转换为2-D(x*b,y)特征矩阵作为模型输入。公式如下:
Input=Reshape(PCA(Dx,y,b))
PCA代表了降维算法;Reshape代表了维度转换函数;Dx,y,b代表了原始特征数据;Input代表了模型输入矩阵;x表示图像的横向长度;y代表了图像的纵向长度;b表示图像的光谱纬度。
当特征被输入到MSC运算方法时,每个卷积核分别计算其特征,最后将生成的多尺度特征融合,其公式表示如下:
温度是影响生物生命活动的最重要的环境因子之一。一般能在45℃以上生长和繁殖的细菌可称为高温菌,主要包括部分细菌,古菌和真菌[10]。ClpP存在于细菌和真核生物中,除了柔膜细菌和部分真菌外[11]。它是高度保守的丝氨酸蛋白酶。ClpP最早发现于大肠杆菌中[12]。ClpP的结构有一个共同点:它包含了14个亚单元,有两个七瓣环形成一个圆柱样结构,该结构围成一个大腔室内含蛋白酶的活性部位[13]。ClpP能形成AAA+(ATP酶联合不同细胞间的活性)伴侣蛋白复合物,它可以使底物变性以及通过轴孔把它们转移到蛋白酶的蛋白水解腔室中进行降解,将蛋白降解成7~8个残基后从腔室中释放出来[14]。
Output=Concatenate(F1⊕F2⊕F3)
Output代表了最终多尺度特征融合后的输出; Concatenate特征融合函数;F1代表了卷积核尺寸为 k-1的运算结果;F2代表了卷积核尺寸为 k的运算结果;F3代表了卷积核尺寸为 k+1的运算结果;⊕代表了融合运算公式。
3 数据集及实验结果
3.1 数据集及评估方法
在这篇文章中,实验是基于三个高光谱公共数据集进行的。第一个数据集是Indina Pines,其大小为145*145,并通过PCA降至到100维,整个图像有16个不同的类。第二个数据集是Pavia University,其大小为610*340,并通过PCA降至到50维。整个图像有9个不同的类。第三个数据集是Salinas,其大小为512*217,并通过PCA降至到29维。整个图像有16个不同的类。总体准确度(OA)、平均准确度(AA)和kappa coefficient (Kappa)被用作评估所提算法策略的性能指标。

表1 部分MSC模块的算法模型
3.2 传统卷积与MSC卷积性能比较
为了比较单卷积与MSC性能哪个更好,在三个数据集上验证了它。构造了一组卷积核尺度由3,4,5组成的MSC和单卷积3,4,5比较。实验一共运行了100轮,每轮迭代20次。实验结果如图4所示。从图4可以看出,本文提出的MSC在特征挖掘和收敛方面都有更好的表现。

图4 收敛曲线(红色线代表了MSC运算。其它颜色线代表了单卷积运算)
3.3 不同模型在不同数据集上的实验结果
为了进行公平的比较,在本实验中,将MSC运算到三个经典的深度学习分割算法中,包括AlexNet[6],ResNet[7],DenseNet[8],并与原算法进行比较。不同数据集的结果显示在下表中(其中表2为Indian数据集;表3为Pavia大学数据集和表4为Salinas数据集)。

表2 提取5%,10%,15%的Indian数据集的样本作为训练集实现分类,其中粗体表示改进算法之后的结果
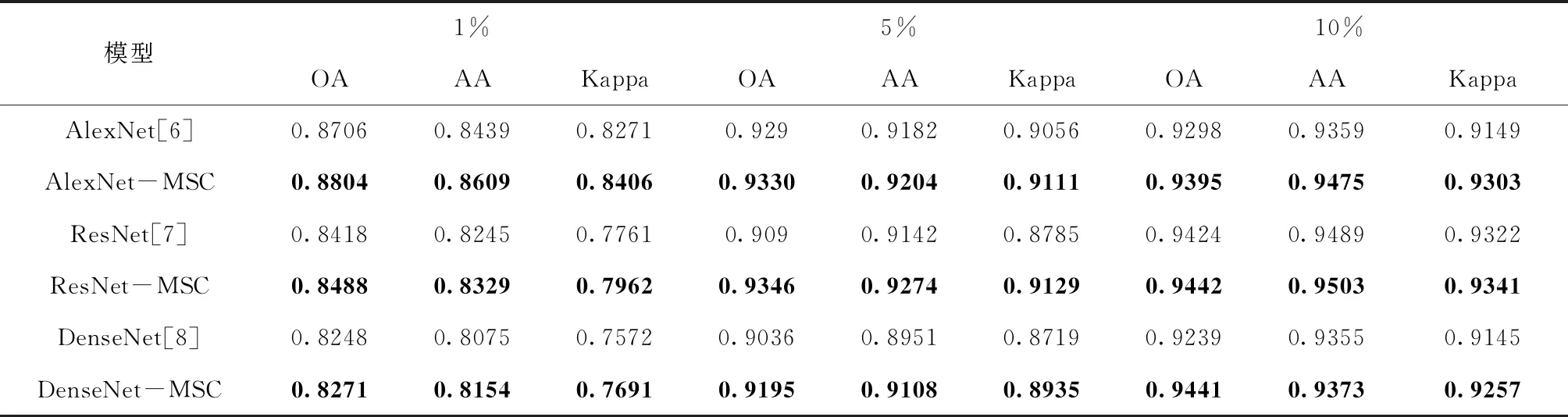
表3 提取1%,5%,10%的Pavia数据集的样本作为训练集实现分类,其中粗体表示改进算法之后的结果

表4 提取1%,5%,10%的Salinas数据集的样本作为训练集实现分类,其中粗体表示改进算法之后的结果
1) Indian数据集的结果:印度松树数据集属于小样本数据集,其中9个类小于500个样本,最小类只有20个样本。从表2中,可以清楚地看到,提出的MSC运算效果比单卷积的效果高2%到4%,对OA、AA和Kappa都是如此。图5对实验结果进行了可视化(使用5%的样本作为训练集进行训练)。可以清楚地看到,改进后的模型显著提高了分类精度(通过红色圆圈展示了原始算法与改进算法在某些地方的明显差异)。

图5 Indian数据集可视化结果
2) Pavia数据集的结果:该数据集分为9类,每类有数千个样本,但样本形状不规则。从表3可以清楚地看出,改进的卷积算法提高了OA,AA和Kappa,并且评估标准随着训练样本数量的增加而显著增加。图6对实验结果进行了可视化(使用1%的样本作为训练集进行训练)。可以清楚地看到,随着训练样本比例的增加,噪声显著降低。相对于传统的单卷积算法,改进的卷积算法的分类效果明显更强。

图6 Pavia数据集可视化结果

图7 Salinas数据集可视化结果
4 总结
针对传统卷积挖掘深层特征会导致部分关键特征丢失,从而给小样本分类带来困难的问题。本文提出了一种MSC卷积运算算法改进了传统卷积运算方式,通过同时计算多个卷积并融合运算后的多尺度深层特征,有效地保留了更多关键性特征。在三个公共数据集和三个改进算法上取得了最好的结果。充分证明了本文方法的可行性。下一步将研究关键特征间的序列问题,从而通过增强特征间的关系来获取更高的分类效果。
