基于密度演化的分布式大数据云存储方法仿真

徐 丽

(湖北工业大学计算机学院，湖北 武汉 430070)

1 引言

互联网大数据、云计算时代快速发展的今天，图片、视频等信息数据存储量需求不断增加，传统单一的存储方法已经无法满足存储需求，而分布式大数据云存储技术具有快速读取、海量处理数据等特点，能够快速有效的存储数据，被广泛应用于云计算中，同时研究学者们发现，在云存储数据的过程中，会产生部分冗余信息，影响大数据云存储的效率[1]。

针对大数据云存储问题，研究相关文献较多，其中丁穗娟[2]首先对待处理数据进行并行特征划分，并使用低负荷传输处理方式，降低存储消耗能量，以此完成海量数据云存储节能存储方法，但是冗余数据问题还能没有能到有效解决，并且该手段对设备要求较高，无法广泛应用在现实生活中。高晨[3]设计一种混合云架构作为云媒资的分布式存储平台，同时为了提高可用性，利用个人私有云和第三方提供商为用户提供能够使的用云数据交换，加强存储数据可挖掘功能使用资源交换战略，完成多方面数据加密方式，有效提高存储方法的安全性。可这样却提高了后续管理难度，并存在存储效果较差等问题。

基于此，本文使用密度演化方式来数据数据存储，密度演化是个体密度随时间变化的过程，将密度演化方法应用在大数据云存储中可有效减少分布式储存中冗余数据，有效增强分布式大数据云存储的准确率与存储效率[4.5]。

2 基于密度演化的分布式大数据云存储方法

2.1 随机系统密度演化理论及其状态概率

研究分布式大数据云存储方法，首先要分析随机系统密度演化理论。通过获取随机系统状态概率来确定函数的密度演化进展。常见性的随机系统可以表示为

X=Gn(Xn，Θ，t)

(1)

式中：Xn表示为n维状态向量；Gn表示为n维算子向量；Θ表示为联合概率密度随机向量；t表示为状态响应时间。从而获得此方程的解析或数值解答。如果存在唯一解，式(1)应转换成式(2)

XI=HI(Θ，t)，X=H(Θ，t)

(2)

式中：XI，HI分别表示为X，H的第I(I=1，2，…，n)个分量；H表示系统状态为联合概率密度随机向量Θ的函数。

在{Θ=θ}时的条件概率密度函数表示为px|Θ(x，t|θ)，θ表示为联合概率密度阈值，x表示为随机系统的数据节点。依据概率相容条件得出

(3)

由式(3)可知，在{Θ=θ}条件下，必有X=H(θ，t)，换言之，在{Θ=θ}条件下，X=H(θ，t)以概率1成立，因而其互斥时间X≠H(θ，t)的概率(及其密度)必为0，可知

px|Θ(x，t|θ)=δ(px(x，t))

(4)

式中：δ表示为Dirac函数，px(x，t)表示为状态概率密度函数。根据条件概率公式，(X(t)，Θ)的联合概率密度函数见式(5)

pXΘ(x，θ，t)

=px|Θ(x，t|θ)pΘ(θ)δ(px(x，t)-H)pΘ(θ)X(t)

(5)

式中，X(t)表示概率密度为pXΘ的边缘概率度函数，pΘ(θ)表示为联合概率密度函数，由此可以得出状态概率密度函数为

(6)

式中：ΩΘ表示为Θ的分布区域。

若将式(2)表示为一个由Θ到X的随机向量变化，就可以由Θ的概率密度函数获得X的概率密度函数。应用复合函数的求导法对式(6)两边关于t求导。如式(7)所示

pXΘ(x，θ，t)=pΘ(θ)·[δ(x-H(θ，t))]

(7)

在复合函数微分法中，可用pXΘ(x，θ，t)表示在{Θ=θ}条件下复合函数的演化规律。据此，获得广义密度演化方程，即

pXΘ(x，θ，t)·δ+x-H(θ，t)=0

(8)

由式(5)得到演化初始条件为

pXΘ(x，θ，t)|t=0=δ(x-t)pΘ(θ)

(9)

演化边界条件可定义为

pXΘ(x，θ，t)|x→±∞=0

(10)

将具有随机参数的随机系统为具有UI及初始条件的动力系统，随机参数引入状态向量，构造增广随机系统，获得联合概率密度的偏微方程。在通常情况下，此方程求解相对较难，为使得一般随机系统可以求解，建立一维广义密度演化方程。从而得出随机系统的状态概率[6]。

2.2 分布式云存储基础模型构建

获取随机系统状态概率后，分析分布式大数据云储存方法[7]。分布式系统采用连通的无向图G=(V，E)描述，其中V表示为顶点集，E表示为边集，所有节点都有同样的传输半径r，WSN网络的变化量φ∈E。分布式大数据的云存储过程会根据分码的结构形成一个包含m个向量组A={A1A2…Am}，A∈V。且每个传输集Si满足以下条件

(11)

为保证数据在任何一次传输过程中都不发生冲突干扰，需要对数据进行完整度检测，其中，AJ描述包含J个已调节数据向量。构建云动态数据采集模型，运用联合特征信息增益提取方法。引入了一个云存储管理因子Ts⊆(0，0.5)，假设被处理云采集数据是可分类的。那么在采集数据集合S。当Ts⊆S，AJ⊆A条件成立时，大数据信息系统状态相应函数表达式见式(12)

(12)

式中：ai表示为大数据信息系统的个数。

根据通信理论中频分复用理论，得到大数据频率与行为关系，常用多普勒效用表示，多普勒频移用公式描述为[8]

(13)

式中，yb表示通信接收端检测到的发射频率变化量；y0表示通信站发射端的载波频率；z表示通信基站发射端的载波频率；w表示传输功率[9]。

在此基础上，构建分布式云存储基础模型表示为

(14)

通过上述设计，得到分布式云存储基础模型，确保大数据传输存储过程中每条数据能够独立存在。为提高分布式大数据存储效率对冗余数据进行分类。

2.3 冗余数据分类

冗余数据会严重影响正常数据的存储，因此需要对冗余数据分类处理。数据在搜集时会出现网络迟延，因此采用局部特性分析方法，依据冗余数据的特性以及相邻领域的数据特征值进行对比，以体现冗余数据的特征。密度演化的分布式大数据云存储冗余数据分配流程图见图1。

图1 冗余数据分配流程图

采用最优分类操作，把冗余数据分类问题转变成最优平面求解的问题

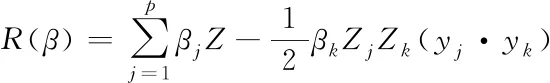
(15)

式中：R(β)表示第二次判别函数，Z表示分类阈值，Zj以及Zk分别表示yj和yk两个向量的分类阈值β描述为权重向量，p表示最大向量，yj·yk为两个向量的标量积，βj描述的是yj向量的权重，βk描述的是yk向量的权重，最优分类平面求解须满足以下要求

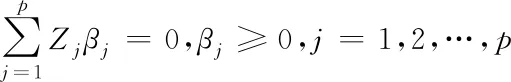
(16)

假设分布式大数据云存储中的冗余数据内的特征产生为非线性转换，那就要使用内积L(yj，yk)替换最优分类函数内的标量积。最优分类平面求解问题可以得出

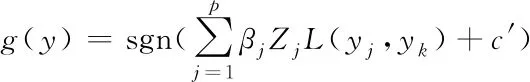
(17)

式中，c′表示为分类别属性；g(y)表示为最优分类函数。该函数可以获取密度演化分布式大数据云存储中冗余数据片段，分类出冗余数据并将其滤除[10]。

2.4 分布式大数据云存储的实现

在上述得出分布式云存储基础框架、实现冗余数据分配的基础上，完成密度演化下大数据云存储方法的实现，传统数据存储算法采用能量谱密度函数，但是该方法造成存储系统中存在较多干扰数据，存储效率地下。对此本文构建以数据特征压缩与密度演化相结合的云存储方法[11]。利用匹配滤波器检测方法对大数据进行预处理，以特征预处理结果作为为输出向量，减少冗余信息，同时为降低存储成本，利用数据特征压缩对数据进行信息降维融合，进行压缩频率普的联合特征识别，让其检验统计量见式(18)

(18)

式中，M表示为云存储节点的采样点数。其中局部性交叉项信息链描述为

(19)

式中，Cb为传输调度中产生的异常数据个数；T为传输调度产生异常数据的时间。f(x)为大数据分布式频谱感知的聚类中心，其公式可以表示为

f(x)=ωe-ωx

(20)

式中：ω表示为频谱感知系数，e表示为功率谱密度，频谱感知节点u的竞争集的定义见式(21)

(21)

通过式(21)产生出的云滴分区区域，构建模糊隶属函数，多源节点中形成新的映射

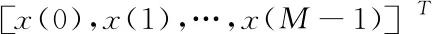
(22)

把文件块和文件块的标签信息关联到S-Table上。设计密度演化特这压缩能量检测器，如图2所示。此时，节点发送数据融合中心的概率为

图2 大数据特征压缩能量检测器

(23)

式中，∂表示为中心数据集。

基于上诉二元假设模型，构建的检验统计量且服从渐进的正态分布，通过能量检测和判决，实现大数据的云存储数据压缩[12]。

与此同时通过构建分布式数据集数实现大数据聚集，减少云存储冗余数据。通过特征压缩，得到大数据的分布式云存储压缩特征识别的虚警概率和检测概率分别表示

(24)

(25)

式中，N表示大数据虚警的统计总合；Pfi表示接受信号的时段数，Pdi表示大数据的配置参数。

将云存储中的大数据特征核函数描述为

(26)

式中，z表示为云存储中的数据集；τ表示为云存储所需的时间。以动态频谱接入的认知技术为基础，得到大数据的变化特征识别数学模型表示为

(27)

对于两个标量时间序列y1和y2，其联合概率函数为f(y1，y2)，计算大数据簇内的灰度相关特征，中心节点点增加功率来发送信标信息，将大数据库的灰度相关特征切分为若干数据块Chunk，由此实现了大数据分布式云存储。

3 仿真分析

为验证提出的大数据分布式云存储方法的有效性，设计仿真。实验采用MATLAB2011a版本作为仿真平台，在该软件中接入Hadoop云平台，并在Hadoop云平台上搭建分布式数据库系统。在oracle数据库内选取100组数据作为实验对象，每组数据包含25个数据节点，每个数据节点占据4个字节，平均分布在200*200MB的分布式网络中。

采用文献[2]、文献[3]方法作为实验对照方法，使用相同实验环境进行仿真。分别采用三种方法对冗余数据分类，得到冗余数据分类准确率对比结果如图3所示。

图3 冗余数据分配准确率对比图

根据图3可以看出中，采用文献[2]方法对分布式大数据中的冗余数据分类，得到分类准确率平均值为78%，采用文献[3]方法得到的分类准确率平均值为83%，准确率均较低。而采用本文方法得到的分类准确率平均值达到了98%，通过上述分析可知，本文方法能够有效分类分布式大数据中存在的冗余数据，节省存储空间。

在此基础上，验证三种方法的耗能及耗时情况，对比结果如图4、图5所示：

图4 分布式大数据云存储耗时对比图

图5 分布式大数据云存储耗能对比图

通过图4可知，在相同数量的分布式大数据中，采用文献[2]方法存储大数据的时间最长，其次为文献[3]方法，本文方法耗时最小，在15s内就能够完成100组数据的存储过程。

通过图5可以看出，在同样的实验环境下，文献[2]方法耗能为80Byte，文献[3]方法耗能为85Byte，本文方法则耗能最低，为30Byte。综合图4、图5能够得出，采用本文方法存储分布式大数据的耗时短、耗能低，有着较高的存储效率。

4 结论

日益增长的云存储需求是现阶段较难解决的问题，同时这也给社会提供了突破创新的路径，通过密度演化能够确定数据在存储过程中存在的冗余信息，通过合理的分配手段，减低冗余部分对云存储的印象，提升整体存储效率。分布式存储结果又可以帮助大数据完成冗余数据分配，最大程度的提升云存储整体效率和精准度。在仿真中得出，本文所提方法能够优秀完成大数据存储任务，并且减低的冗余数据和提升数据分配精准度，为社会日益增长的大数据提供的长远的存储方法，适用于各个领域中，可广泛运用在现实生活中。

同时，实验证明本文方法虽然能够减少冗余信息，提升了方法效率，但是却不能够完全的杜绝冗余数据的产生，那么接下来的研究方法就是如何通过使冗余降低至最小，甚至是可以忽略不计的程度，使得可以不计算冗余分配，由此减少方法步骤，在最大程度上提升方法的运行效率，以便更好的运行在现实环境中。