基于GRU网络的气象要素预测算法
2021-11-17王怡婷鞠兴旺陈北京
王怡婷,陈 曦,鞠兴旺,陈北京,2
(1. 南京信息工程大学计算机与软件学院,江苏 南京 210044;2. 南京信息工程大学江苏省大气环境与装备技术协同创新中心,江苏 南京 210044 )
1 引言
气象要素指某地区特定时刻下的大气物理指标和天气现象。气象要素变化与人们的经济活动息息相关,因此气象要素预测可对极端天气预警、军事分析和期货投资等提供很好的指导作用,从而帮助各部门根据天气变化提前进行统筹安排[1]。比如,在极端天气灾害预警中,气象要素预测可以为人员提前撤离和财产保护提供帮助,减少相关人员的伤亡和财产损失。
国内外学者最早采用模式预测法对气象要素进行预测,即利用天气学、动力学等气象理论,在初始条件和边界条件下探究相应要素的变化规律。曾庆存[2]早在1963年就从大气流体力学的角度对线性和非线性系统预测方程进行了思考,还原其物理过程。Marchuk等[3]首先介绍并总结了一些短期天气预测的算法,然后提出改进算法以提高预测精度,在正压模式中使用平衡方程,在斜压模式中采用准地转近似算法。不过,这类模型的搭建普遍需要运用大量的假设,存在许多限制,与实际情况具有一定差异。因此,有学者引入了基于统计的算法。这类算法通过统计某一现象在过去一段时间内特殊情况下出现的频率,推测未来一段时间内相似环境下这种现象出现的概率。比如张晨阳等[4]使用改进的贝叶斯算法对气象数据进行处理。蔡舒平[5]等探讨了基于Fisher算法的短期负荷预测,很好的利用了气象因素的累积效应。但是,此类算法会出现一些由统计本身带来的误差,使预测精度受到一定影响。
随着相关观测设施不断升级,观测所得数据呈几何级数增长[6]。巨大的数据量导致传统的算法已无法满足人们对于气象要素预测实时性越来越高的要求。因此,一些基于机器学习的算法随之出现。Kwong等[7]使用人工神经网络进行风力预测。黄豪南等[8]结合季节性差分自回归滑动平均(SARIMA)模型和BP神经网络对气要素进行预测。任才溶等[9]首先利用K-Means算法对原始气象数据聚类,然后利用欠采样方法对数据进行平衡采样,最后利用随机森林构建PM2.5浓度等级预测模型。Gao等[10]在台风踪迹的临近预测中,通过使用长短期记忆网络(LSTM)与主观经验法以及区域数值模拟法进行对比,发现在24h间隔时LSTM的预测误差低于后两者。不过,现有基于机器学习的气象要素预测研究主要是由单一要素的历史数据预测其未来时刻。而各气象要素之间是有相关性的,并且这些相关性对预测是有帮助的。当然,各气象要素之间的相关性难以用单个方程拟合出来。
因此,本文将多项气象要素输入到深度网络中相互作用。从两方面解决现有工作存在的问题:①能够处理大量的气象数据,同时减小了气象要素大数据在统计计算过程中不可避免的误差;②将各要素之间较为复杂的非线性变化关系交由深度网络结构来处理,通过带标签的监督学习过程将多项气象要素输入结果进行输出。具体来说,本文提出了一种基于控循环单元(GRU)网络的气象要素预测模型,输入8项相关的气象要素,输出基本表征大气状态的3项要素(气温、湿度和气压)的预测结果。GRU网络是LSTM网络的一种简化变体,在性能相近的同时对数据的处理速度较优,而LSTM网络由于其特殊的记忆门和遗忘门的结构,已在文献[10]中体现较高的优越性。
2 提出算法
2.1 GRU
在处理时序相关的信息时,卷积神经网络(CNN)会忽略信息之间的时序信息。为了弥补这样的缺陷,作为一种由节点定向连接成环的人工神经网络,循环神经网络(RNN)利用内部的记忆处理时序信息。不过,在时间间隔不断增大后,RNN也易于丧失远处单元的信息,这使得部分重要信息在训练中逐步减少以及大量无用信息带来的错误逐步累积。为了解决这样的问题,LSTM、GRU等结构利用门控结构对网络中的信息进行筛选。LSTM通过输入门控制是否允许写入,遗忘门控制记忆单元的值是否需要更新,输出门控制是否允许输出。三个门的作用在于让LSTM能够记住更久远处的有效历史信息,避免梯度的爆炸和消失问题。但由于LSTM的结构较为复杂,Chung等[11]在2014年提出一种新的变形GRU。它在保证与LSTM相当精度的条件下简化了网络结构,提高了效率。具体结构如图1所示。

图1 GRU网络结构示意图
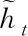
rt=σ(Wr·[ht-1,xt]),
Zt=σ(Wz·[ht-1,xt]),
(1)
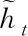
2.2 所提算法
由于GRU网络较LSTM网络在性能相近的同时对数据的处理速度较优,因此本文基于GRU网络模型提出了一种气象要素预测模型。为了学习更深层次的特征以及提高网络的拟合能力,输入的气象数据经过双GRU处理。具体模型结构如图2所示。模型对未来表征大气状态的气象要素(气温、湿度、压强)的逐小时变化进行预测。输入数据序列X={X1,X2,…,Xn},其中n为选取的与预测相关的气象要素个数,每个数据Xi由选取的多项相关气象要素组成。本文选取了8项气象要素,因此在图3中使用8种不同颜色表示。这些气象数据经过双GRU处理后再通过全连接层FC将所学习到的特征进行线性映射得到预测结果。
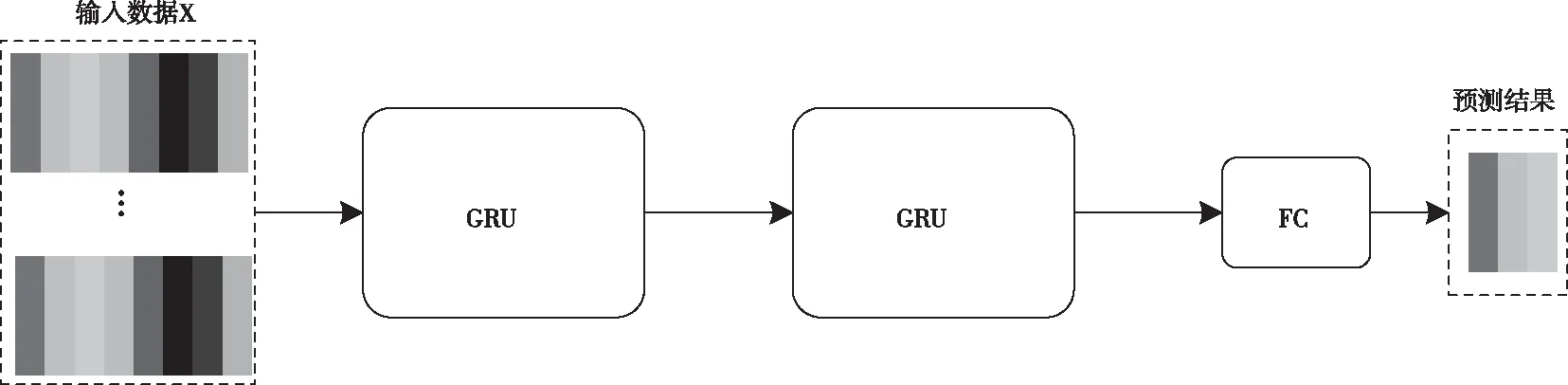
图2 基于GRU的气象要素预测网络模型
算法具体步骤如下:
1)以固定的时间间隔在数据集中选取数据序列,每一个数据包含预测相关的8项气象要素。重复这样的步骤从原始数据集中提取出训练数据。
2)将气象数据以时间序列输入到GRU网络中,首先按照式(4)中的前两个公式,由当前时刻的输入数据以及其上一时刻的输出通过重置门和更新门得到当前时刻的状态值rt和Zt。然后按照式(4)中的后两个公式,由上一时刻的输出和重置门的状态值通过tanh函数激活得到当前时刻的状态信息候选值,最后由该候选值和更新门的状态值计算得到当前时刻的输出。按照此过程得到所有时刻的输出。
3)将步骤2)所得的所有时刻的输出作为第二个GRU网络的输入,然后进行与步骤2)相同的迭代过程。
4)将步骤3)所得的输出结果作为全连接层FC的输入,通过FC层对提取的特征进行线性映射,最终得到3项气象要素的预测结果。
整个网络中使用的激活函数均为tanh激活函数,它由Sigmoid函数变形而来,表达式如下

(2)
相比于Sigmoid,tanh函数的输出以0为中心。而在气象要素预测应用中一些气象要素拥有正负极性,比如气温,并且tanh函数收敛速度更快,因此选择使用tanh作为激活函数。
为了更好地训练网络,采用均方根误差(RMSE)来衡量提出模型的损失值。t时刻包含m个气象要素的预测结果的损失值Lt为
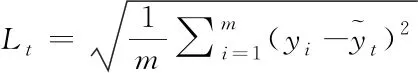
(3)


(4)
3 实验与分析
3.1 实验数据及预处理
本文所用实验数据来源于中国气象数据网(http://data.cma.cn)中的2018年南京市基本气象要素逐小时观测资料。原始数据共包含24项气象要素。为了对大气状态进行较好的预测分析,依据大气科学学科经验选取了与大气状态相关性较高的8项气象要素作为输入3项气象要素进行预测输出。输入的8项要素包括温度、湿度、气压、水平能见度、两分钟平均风速、降水量、总云量和水汽压。输出的3项气象要素为温度、湿度和气压。其中,选取了约5000个小时的数据进行实验,训练集与测试集的样本比例为4:1。不同时间间隔下的训练集和测试集的样本数如表1所示。

表1 不同时间间隔下的训练集与测试集的样本数
另外,由于一些自然、人为和仪器等因素,选取的气象数据网上的数据存在数据缺失和异常数据等问题。对于异常的数据,通过观察某一要素或某几项要素的波动范围,若明显超出正常范围,这一组数据将被全部剔除出数据集。对于缺失的数据,采用线性插值的算法进行填充,即

(5)
其中,xt是t时刻缺失的值,xt+1是缺失值下一时刻t+1时刻的值,xt-1是缺失值上一时刻t-1时刻的值。
在完善整个数据集后,最后对所有数据进行了归一化处理。此处采用最大最小法进行归一化,即,
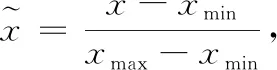
(6)
其中,x为某项气象要素的原始值,xmax为其最大值,xmin为其最小值,为归一化后的值。
3.2 实验结果对比
为了验证所提算法的效果,将提出的算法分别与基于CNN、CNN+LSTM、LSTM+LSTM算法进行对比,从而体现采用GRU相对于CNN和LSTM的优势。基于CNN的算法采用密集卷积网络(DenseNet)提取特征,而基于CNN+LSTM、LSTM+LSTM算法就是在图3所示的所提算法中将GRU+GRU组合分别由CNN+LSTM和LSTM+LSTM代替。所有算法的训练和测试均在如下实验环境中进行:11GB GeForce GTX 1080 Ti显卡,3.20 GHz i7-6900K CPU和65GB内存的服务器,Keras和Tensorflow深度学习框架。实验中对湿度、气压和温度3项要素进行预测,因此下面将分别对每项要素进行对比分析。
对表1所示的3个不同时间间隔的数据集分别进行训练和测试,测试集的3项气象要素(湿度、气压和温度)的平均RMSE值如表2所示。从表2可以发现:a) 对于所以对比算法和所有气象要素,预测误差均随时间间隔的增大而增大,这与现实中短期预报较中长期预报更准确相一致;b) 提出的基于GRU+GRU的算法与基于LSTM+LSTM的算法性能相当,基于GRU+GRU的算法在间隔较小时更优,这说明GRU确实是LSTM的有效变体,它保留了LSTM的重要特征,而且速度更快(详见表3);c) 上述两种算法均优于基于CNN的算法以及基于CNN+LSTM的算法,这进一步印证了LSTM与GRU在预测应用中较CNN更有优势。
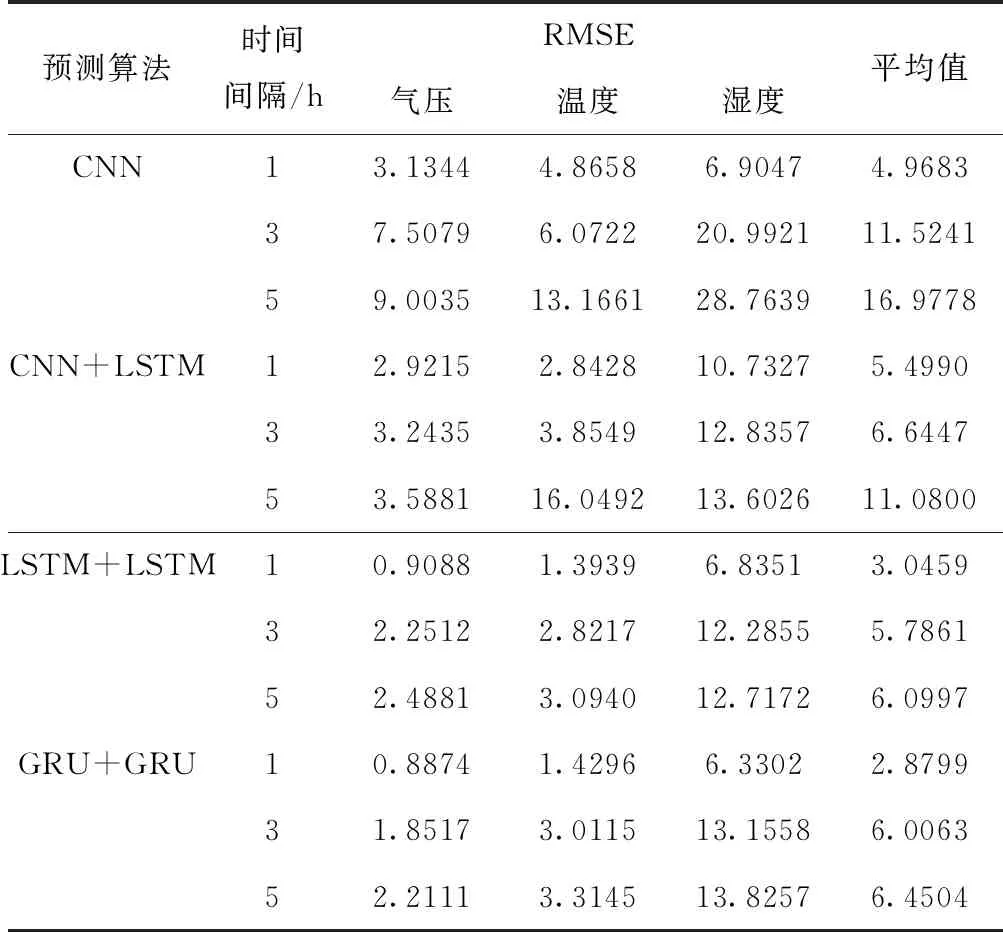
表2 不同预测算法对3项气象要素的预测误差RMSE值对比
同时,论文中还对比了各算法在相同网络层数下的训练时间,如表3所示。这里对比的是时间间隔为3h的情况。从表3中可以发现CNN训练所需时间最少,这是由于CNN的结构比LSTM以及GRU都更简单。当然,提出的基于GRU+GRU的算法也快于基于LSTM+LSTM的算法,训练时间节省近一半。这是因为GRU比LSTM少一个门函数,从而参数量少于LSTM。

表3 时间间隔为3h时各算法训练所需时间对比
4 结论
本文提出了一种基于双GRU网络的多项气象要素预测算法。该算法利用连续两个GRU神经网络对多个相关的气象要素进行处理,并最终得到多项气象要素的预测结果。这不仅解决了传统算法无法有效处理大量气象数据的不足,而且还弥补了现有基于机器学习算法只是利用单一气象要素的历史数据对其自身进行预测的缺陷。通过实验发现如下一些结论:1) 气象要素预测精度随着预测时间间隔的增加而减小;2) 与传统CNN网络相比,LSTM和GRU在预测精度效果均显得更优,且这个优势随着预测间隔的增加而愈加明显;3) 基于GRU的算法在训练所需时间上也更优。与实际气象要素预测业务追求的快速高效的需求相一致。
