城市生态景观色彩平衡性布局最优规划仿真

梁立群

(长春师范大学，吉林 长春 130032)

1 引言

城市生态景观的均衡化建设是改善环境的必然趋势，但由于我国此方面技术尚不完善，人工制造的生态景观不仅耗费巨大的经济财产，后期维护也比较困难，因此绝大部分城市生态景观都来源于自然条件。生态景观是联系城市与自然之间的桥梁，实现生态景观的建设不但可以满足人们的居住要求，更能保护自然景观。

目前城市景观规划问题得到了很多专家重视，也出现了一些较好的研究成果。文献[1]提出基于城市绿地系统空间布局优化的景观色彩布局规划方法，组建城市景观状态合理性静态评价模型，提取最佳的城市色彩景观空间格局的可达性特征参数权重，基于多维特征参数，构建城市色彩景观合理布局优化设计模型，采用变尺度混沌方法组建城市景观状态合理性静态评价模型，提取最佳的城市色彩景观空间格局的可达性特征参数权重，确立城市色彩景观合理性布局优化设计指标体系。但该方法无法计算出城市色彩景观合理性特征最佳权重，存在设计效果差的问题；文献[2]提出基于景观生态学的色彩布局规划方法，采用生态景观学的斑块廊道基质理论、生物多样性理论以及景观异质性理论来对城市景观色彩布局进行分析，基于模糊评价标准对评价体系中的量化定性指标进行评分，并对色彩景观合理性指标权重进行计算和一致性检验，并计算其计算综合评价值，并组建城市色彩景观合理布局优化设计模型，实现城市生态景观色彩布局的最优规划。但该方法景观色彩布局平衡性较差，应用效果不理想。

针对传统方法存在的问题，提出新的城市生态景观色彩平衡性布局最优规划方法。利用色彩平衡原理对城市生态进行计算，获得生态景观指标，分析对比度、信息熵、相关系数以及角二阶4种纹理特征，引入最大似然法对其生态景观数据进行分类，完成景观布局最优规划。以真实数据作为实验前提，经实验验证研究方法可以有效改善城市烟尘含量，并降低空气中二氧化硫含量，在一定程度上，也提升了该地区的降水量，对城市生态优化具有实际作用和效果。

2 景观色彩平衡性布局原理

2.1 色彩空间描述

色彩描述主要对颜色的三种刺激分量信息的描述，描写颜色色貌分量的分布比例。RGB色彩平衡性是非常典型的色彩描述方法，其待测光匹配满足格拉斯曼定律[3]，具体R、G、B三刺激值如下列公式所示

C[C]=R[R]+G[G]+B[B]

(1)

其中

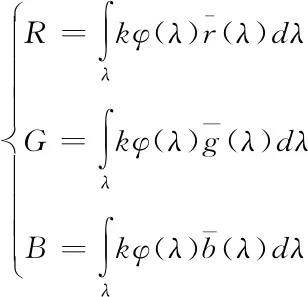
(2)

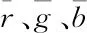
2.2 色彩平衡条件

综合描述色彩方法是依据CIE1931的标准色度系统，将RGB的分量进行转化至XYZ色域中，其变换公式如式(3)

(3)

式中：X、Y、Z是此色彩空间中的三种刺激值。

再利用下列色品坐标公式，可以获取解算值待测样色在色度系统内的准确位置。

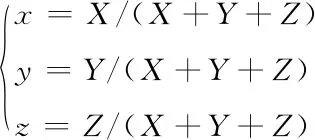
(4)

式中：x、y、z是景观色品坐标[5]。

2.3 生态景观指标

通过景观指数与空间的分析方法，能够定量化获取地形和景观结构特征之间的关系，准确评估景观结构状况，从而更好解释景观结构与功能之间的互相关系，最后以此为基础调整保护生态环境与经济结构[6]。

生态景观格局反映的是景观要素在空间中的聚集与分散，其要素在于空间的分布位置、大小、类型、方向、形状以及方向。定量分析景观格局是构建景观构造、现象和过程的联系，能够更好的解释和理解景观功能。景观生态学家对于景观的空间格局提出了多种评估指标。

1)多样性指数

设定某种嵌块类型i的个数为m，面积为aij，则此种类嵌块的面积公式为

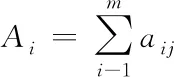
(5)

在该基础之上，利用GIS的空间分析其功能获得景观要素转移矩阵。

景观的香农多样性指数用来反映景观要素的多少，以及所有景观要素的占比变化。当所有景观的素面积相等时，其景观的多样性最高，利用Hmax进行表示

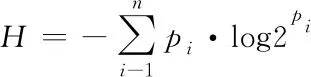
(6)

式中：pi代表景观类型i所占据的总面积比，n代表类型的总数。

景观的香农均匀度指数E用来叙述不同景观要素的分配均匀程度，其公式如下

E=H/Hmax×100%

(7)

2)优势度

优势度是用来对测度景观的结构内一种或者是多种景观类型的支配景观程度，具体的计算公式为

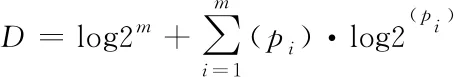
(8)

式中，D代表优势度，pi与m之间含义与式(5)相同。D值越小代表景观类型之间比例较为相近；而D值较大时代表景观只是受到一种或者极少数的几种类型进行控制的。不过需要指明的是，当D=0时，此类指数在完全同质性的景观内是没有作用的，。

3)破碎度

破碎度是通过以单位面积中的版块数测度反映景观斑块的破碎程度，具体计算公式为：

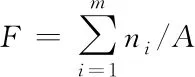
(9)

式中：F代表景观的破碎程度，ni代表第i类的景观类型斑块个数，A代表景观的总面积。F越大，则代表景观的斑块越破碎。

4)分维度

以往研究证明，相对于其它所有景观类型的形态以及结构，景观中的镶嵌体是最为典型的分形几何体，可以利用分形理论来研究定量化，再以周长的形状度量的分维数对几何形状特征参数进行描述。因其它所反映的图形形状视为周长的函数随周长变化而变化，同时还能够对景观镶嵌体的分形结构进行定量化测试。景观类型分维值模型公式如下

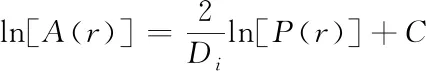
(10)

式中：A(r)代表面积，P(r)代表周长，r代表度量尺度，Di代表二维欧式空间内的分形维数，C代表常数，依据所有斑块的周长以及面积数据，构建形状如上式的回归模型，即能够获得此景观类型的分形维数Di。Di的大小代表了此景观类型的稳定性和复杂性，具体的数值理论范围在1～2之间，其值越大，代表此景观的类型形状越复杂；Di=1代表景观斑块的形状是正方形；Di=2代表景观斑块的形状最为复杂。此外，利用分维数Di能够相对的比较其景观要素格局特征，以此确定不同生态因子对于景观格局的影响，如果两种景观格局要素具有相同的分维数，则说明两者存在一定格局差异。

分维数是反映景观总体特征的重要指标，可以在一定程度上反映出生物活动对景观格局的影响程度，例如：在受到干扰较小的自然景观通常是呈现出一种复杂的景观形状，分维数相对较大，而人工经营的景观其大多数是呈现简单的几何形状，分维数较低[7]。

3 城市生态景观最优规划

通过分析对比度、信息熵、相关系数以及角二阶4种纹理特征对城市生态景观图像纹理进行分析，利用最大似然法对其生态景观的数据进行分类，以此实现布局的最优规划。假如n″代表像素值；p(i″，j″)代表景观图像共生矩阵内第i″行、第j″列的元素；(i″，j″)代表生态图像的共生矩阵灰度值，通过上述方法对实际应用比较广泛的纹理特征叙述向量，分析城市生态景观图像纹理，选择的纹理特征所描述的向量其分别是信息熵ENT、角二阶矩ASM、对比度CON以及相关函数COR。即具体的计算公式如下所示[8]

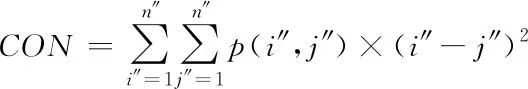
(11)

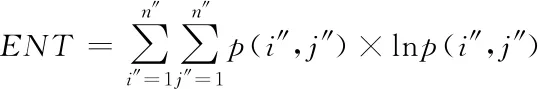
(12)

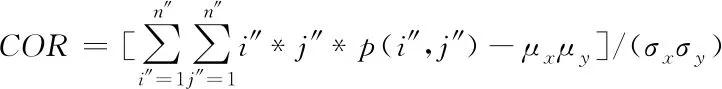
(13)

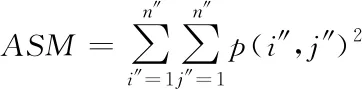
(14)

式中：μx、μy与σx、σy分别代表生态景观图像位于x轴与y轴中的均值与标准差，式(11)代表生态景观粗糙纹理，假如元素p(i″，j″)在主对角的周围，则生态图像的对比度CON值最小，再假如元素p(i″，j″)相距生态图像最远[9]，那么对比度CON值最大，式(12)所代表的是度量景观图像的纹理特征能量，式(13)所代表的是景观图像灰度共生矩阵的所有元素之间的相似程度最重要指标，而式(14)是对于生态景观图像的灰度分布均匀程度的度量标准[10]。

基于城市的生态景观的图像所有方向θ(0°、45°、90°以及135°)灰度矩阵都能够计算获得以上4个纹理特征值，相对于生态景观图像的4个方向所有灰度共生矩阵，所有矩阵特征纹理都对着4个不同方向的数值，若M(d)代表以上所计算的4个纹理特征描述向量在4个方向的均值，即能够获得城市生态景观图像的角二阶矩阵均值、图像对比度、相关系数以及信息熵，其具体的计算公式分别如下所示

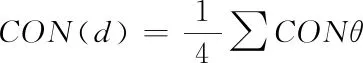
(15)

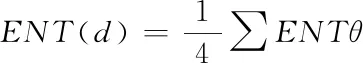
(16)

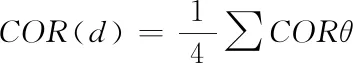
(17)

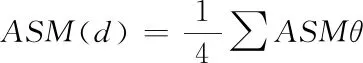
(18)

依据统计城市生态景观图像的所有纹理特征差异值情况，同时在与上述的生态平衡指数相结合，对生态景观所采用的最大似然法进行分类，实现布局的最优规划[11]，其公式如下

(19)

式中：Φ代表生态景观的类别集合，X代表生态的景观的纹理特征描述向量，P(We/X)代表X落入We的概率，依据式(19)的概率值能够对生态景观的布局进行最优规划[12]。

4 实验结果与分析

为证明研究方法的有效性，以MATLAB7.2软件为平台进行实验，某城市真实生态景观数据如表1。

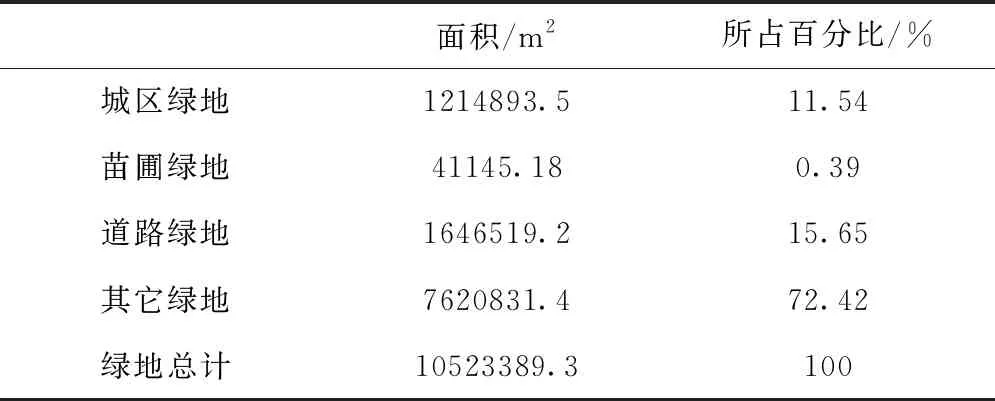
表1 城市生态景观统计表

依据上表1看出，本文所选取的城市其生态景观色彩平衡的数据信息需要与该地区所产生的生态因子数据信息进行对比，其中生态因子主要是来源于历史的统计，具体如表2所示。

表2 2012年～2018年城区历史生态平均数据

利用研究方法对2012年～2018年的该地区生态进行规划，仿真具体数据结果如图1～图2所示。

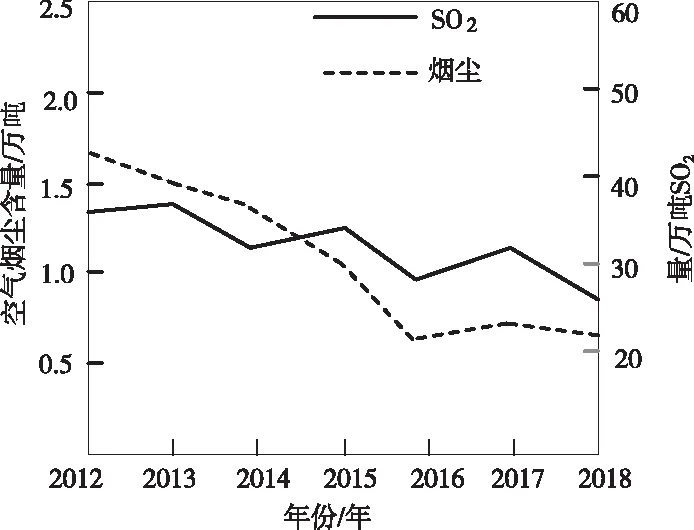
图1 研究方法下烟尘与SO2量的数值变化

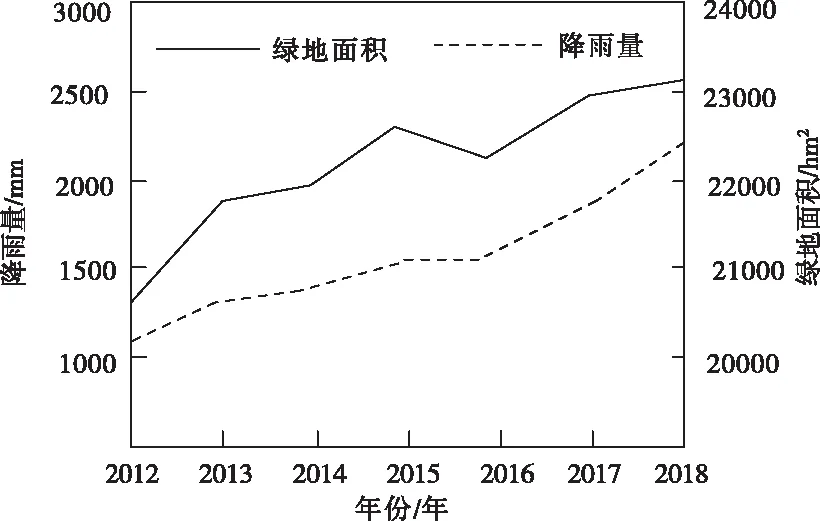
图2 研究方法下城市降雨量与绿地的数值变化

将图3与表1的生态产量测试结果进行对比可知，研究方法在应用后，有效改善了城市的实际环境问题，对比2012年～2018年数据可知，研究方法使得该城市的二氧化硫和烟尘的含量明显降低，且降雨量和绿地面积均有所增多。研究方法充分考虑到其生态景观的区域、面积以及占比等情况，并且规划生态景观存在多样性，使其在测试的时间段内该城市的环境问题得到了有效的控制。

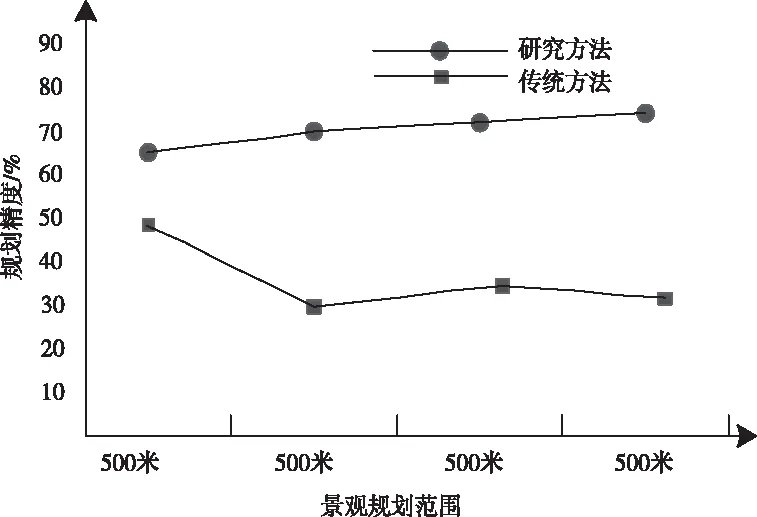
图3 景观规划精度对比

为进一步通过仿真验证研究方法的有效性，在上述实验基础上，对不同方法的城市生态景观色彩平衡性布局最优规划的精准度进行实验。精度越高，说明方法应用过程规划的精细度高。若方法的精准度偏低，会直接导致景观规划效果粗略问题，无法达到目前该领域的基本要求。

由图3实验结果可知，两种方法在景观规划过程中精度均出现了波动，但研究方法精度波动更小。在合理的景观规划长度范围内，研究方法具有更高的景观规划精度，说明研究提出的方法应用精细度更高。通过上述实验证明研究方法对城市生态景观色彩平衡规划具有良好的效果，可以具体的改善其生态环境质量问题。

5 结束语

传统的布局规划方法不能较为显著的改善生态质量问题，提出新的城市生态景观色彩平衡性布局最优规划方法。通过对比度、信息熵、相关系数以及角二阶4种纹理特征对城市生态景观图像纹理进行分析，利用最大似然法对其生态景观的数据进行分类，实现最优规划。仿真结果证明了研究方法对生态景观质量问题有明显改善作用，其效果良好。