基于Hammerstein模型的阀门粘滞检测和量化

2021-11-17王志国

计算机仿真 2021年7期

江钊，王志国，刘飞

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122)

1 引言

阀门粘滞是实际工业过程中的一种常见现象。它通常会造成控制回路性能衰减，严重时会导致回路振荡，进而影响到产品质量、系统能耗、以及工厂利润。据统计，有20%-30%的回路振荡是由阀门粘滞引起的[1]。因此，阀门粘滞现象的检测和量化研究具有重要实际意义。目前，粘滞的检测方法可分为侵入式方法和非侵入式方法。所谓侵入式检测就是在离线状态下对阀门进行行程测试和撞击测试，以获得阀门的工作状态。而非侵入式检测则是在阀门处于工作回路中进行的，通过在线采集回路或阀门的输入输出数据，然后再根据某些数据处理算法判断是否有粘滞存在。

控制领域的研究者更侧重阀门非侵入式检测的研究。2004年，Kano等[2]提出来两种粘滞检测方法。方法一是根据阀门粘滞时控制器输出增大而阀位信号(MV)不变这一特性提出的；方法二是基于控制器输出信号与阀位信号之间的平行四边形关系提出的；这两种方法共同的缺点是必须知道阀位信号。Brasio等[3]利用近似于阀位信号变化趋势的变换函数，提出来一种粘滞检测方法；该方法可以应用在液位回路和被控过程带有积分环节的控制回路。Horch[4]在互相关函数方法的基础上进行改进，提出了一种基于过程输出信号的二阶导数的概率分布特性检测方法，克服了原方法不能应用在液位回路这一缺点。He等[5]受到粘滞存在与否控制器输出信号(OP)和过程输出信号(PV)会展现出不同的形状这一特性启发后，提出了一种图形拟合的方法。Rossi和Scali[6]在He的方法上进行了改进，通过使用正弦波、三角波、继电器波对过程输出信号进行拟合，以检测阀门粘滞。Singhal和Salsbury[7]提出了一种根据偏差信号峰值前后面积比较的粘滞检测方法，其不足是容易受到外界干扰影响。Daneshwar等[8]提出用模糊聚类算法对回路中的粘滞进行检测，并根据聚类中心连线斜率的变化定义了一个新的粘滞指标。郑丽丽等[9-10]在Daneshwar的方法基础上增加了四边形的凹凸性识别，克服了原方法容易将外部干扰误诊断为粘滞这一问题。

上述阀门粘滞检测方法都是基于信号的粘滞检测方法，其检测结果可能会出现误判断、且易受到干扰影响、有些诊断指标存在盲区。

本文通过双向干谱法检测非线性、椭圆拟合法判定粘滞、粒子群优化方法结合Hammerstein模型方法量化粘滞等步骤，提出了一种新的粘滞检测和量化。其相比传统方法检测结果更准确，抗干扰能力也有所增强。

2 阀门粘滞模型

气动调节阀是实际工业中使用最多的一种阀门。其结构如图1所示，主要由隔膜、弹簧、阀芯、阀杆、填充物、进气口组成。阀芯和阀杆以及隔膜相互连接，当阀芯上移时，阀门打开，阀芯下移时，阀门关闭。长期使用中，由于密封退化、润滑油消耗、阀杆和填充物之间的摩擦力等原因，阀杆所受摩擦力发生变化，从而出现粘滞现象。

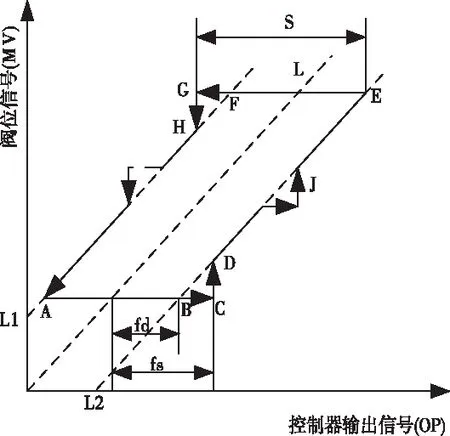
图1 气动阀门原理图

阀门粘滞特性的表现现象为滑动前的突然跳变，其输入输出关系如图2所示。直线L表示阀门没有粘滞时的输入输出关系。当阀门存在粘滞时，随着控制器输出信号的变化，阀位信号沿着A→B→C→D→E→F→G→H→A循环运动。从图中可以看出，整个循环可分为四个状态：AB段为死区，BC段为粘滞，CD段为粘滞跳变，DE段为平滑运动，粘滞参数S=AB+BC，J=CD。其运动过程为：偏差的存在使得控制器输出逐渐增大，此时阀门位于死区保持静止状态；OP增大到能够克服B点时，阀门进入粘滞区保持粘滞状态；当OP足以克服静摩擦力到达C点，阀门瞬间跳变到D点开始DE段的平滑运动。控制器反向输出时，阀门运动过程与之类似。

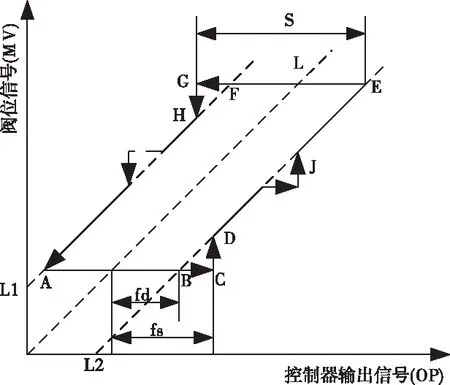
图2 典型的粘滞阀门输入输出特性图

粘滞模型是阀门粘滞问题研究的基础，通常分为物理模型和数据驱动模型。物理模型需要大量的阀门生产数据，建模和使用都不方便。现有研究更侧重于数据驱动模型[11]。2015年Li等[12]在传统数据模型基础上提出了一种新的模型。Li模型不仅能够完整的描述阀杆的四个运动状态，而且在阀杆从一个方向转向另一个方向时细节处理得很完善。

3 粘滞的检测

阀门粘滞是导致控制回路性能欠佳的问题之一，除此之外的其它因素有：外部干扰、控制器参数不佳等。本文假设在众多影响控制性能的因素中只有阀门问题为非线性特征，其它都为线性特征。此条件为目前控制性能诊断研究的常用条件，如文献[13]。检测的基本思路如下：第一步，采用双向干谱法进行非线性的检测；第二步，利用控制器输入和回路输出信号特性进一步确认粘滞。

3.1 粘滞非线性检测

存在粘滞的阀门在其输入输出特性上表现为一种非线性函数关系，而存在非线性特征的控制回路会产生非高斯和非平稳的时间序列。

对于实际工业中的带有阀门的控制回路而言，一般能够采集的数据有控制器输出信号、过程输出信号、设定值(SP)。控制偏差信号相对更加稳定，能准确反应出控制回路状态。因此，本文对控制偏差信号进行双向干谱分析以检测回路中是否存在非线性[14]。首先，用双向干谱法计算偏差信号的非高斯性指标NGI和非线性指标NLI，其详细计算方法如下：

计算双频谱B(f1，f2)

B(f1，f2)=E[X(f1)X(f1)X*(f1+f2)]

(1)

其中，B(f1，f2)表示在双频率f1，f2处的双频谱，X(f)是任意时间序列的离散傅里叶变换，*表示共轭复数，E表示为数学期望。

双频谱经过归一化处理后定义为双向干谱，其值在0到1之间，其公式定义如下：

(2)

其中，bic2表示双向干谱函数的平方。

为了检测测试信号的高斯性和线性，定义了非高斯性指标NGI如下

(3)

(4)

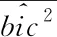
定义非线性指标NLI公式如下

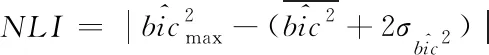
(5)

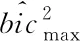
若NGI小于或等于NGI阀值，则控制偏差信号是高斯信号，相反，若NGI大于NGI阀值且NLI大于NLI阀值，则控制偏差信号是非高斯非线性信号。图3所示为非线性检测过程的基本步骤。

图3 非线性检测流程图

在不同数据长度时非高斯性指标NGI阀值和非线性指标NLI阈值可按照文献[13]中的表1选取。通常情况下，尽量选取4096个数据长度作为样本，对应的NGI阀值为0.001、NLI阈值0.01。用双向干谱法对控制偏差信号按照图3步骤进行分析，若检测结果是非线性，控制回路性能下

表1 NGI和NLI阈值表

降的原因是阀门非线性；若检测结果是线性，控制回路性能下降的原因可能是外部干扰或控制器参数不佳。

3.2 粘滞特性的判定

阀门非线性并非阀门粘滞一种，还包括间隙、死区和饱和等。确定回路中存在非线性特性后，再根据PV-OP图进一步对粘滞进行判定。研究发现，粘滞在控制回路中会产生极限环现象，该现象在PV-OP图中表现为椭圆循环模式。可以根据这一特点判定非线性的类别是粘滞。具体步骤如下所示：

1) 选择一个数据段长度L，如1500，将采集的数据按照L分为若干小段。

3) 将规律因子最大值记为rmax，并将对应的Tp记为Tpmax。若L大于4Tpmax，将L更新为L=4Tpmax，跳转到步骤2)；若L小于4Tpmax，跳转到步骤4)。

4)rmax对应小段的OP和PV数据分别定义为OPf和PVf。

5) 对OPf和PVf数据用最小二乘法求得椭圆拟合曲线。

定义沿OP方向椭圆最大宽度为粘滞指标AP，用来判定粘滞的存在，其公式如下所示

(6)

其中，m和n分别表示拟合椭圆主轴和副轴的长度。α为椭圆旋转角度。

由式(6)中的参数描绘的椭圆拟合曲线和PV-OP曲线很接近时，说明回路中出现了极限环现象，由此判定回路中的非线性类型是粘滞。

4 粘滞的量化

粘滞程度不同，其对控制系统的影响也不同，后续工程师对其处理手段也相应不同。程度很小的粘滞对控制系统的影响可忽略，阀门也可以继续使用。程度大的粘滞会使控制性能下降，严重时表现为回路振荡，同时阀门寿命快速减少。另外，粘滞量化也是后续补偿的基础。

存在阀门粘滞特性的控制回路可以用Hammerstein模型来描述，其结构如图4所示。模型可分为两个部分：一部分为阀门动态加上被控过程，此部分是线性部分；另一部分为具有粘滞特性的阀门，是非线性部分。

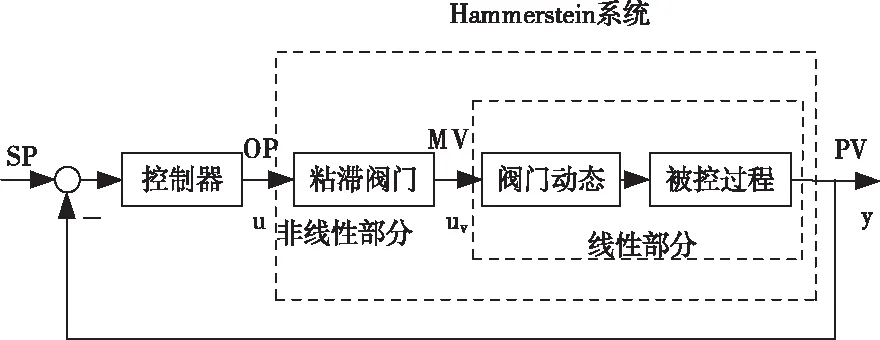
图4 带有粘滞阀门的控制回路框架图

选用ARX(m，n，τ)模型来描述上图中的线性部分

y(k)=ΘT[y(k-1)，…，y(k-n)，

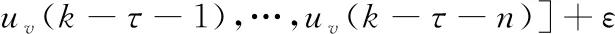
(7)

其中，y(k)表示模型输出，k是时间序列，取值为1到N，uv(k)为模拟输入信号，这里可理解为阀门位置的一种变换形式，τ表示延迟时间，ε表示噪声，向量Θ形式如下

(8)

它是过程对象的参数向量，式中的a1，an，b1，bn均为ARX模型系数。

图4中的粘滞阀门为一非线性环节，其输入为控制器输出信号u(k)，其输出可用一非线性函数表示如下：

Uv(k)=NLstic(u(k)，…，u(0)，uv(k-1)，..，uv(0)，S，J)

(9)

其中，Uv(k)表示阀位信号，S和J分别为阀门的粘滞参数。

定义预测误差

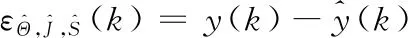
(10)

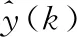
然后，再定义如下目标函数

(11)

其中，k取值为1到N，和分别为粘滞参数的估计值，为过程对象的参数的估计值。

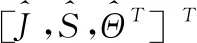
(12)

进一步定义矩阵

(13)

(14)

目标函数可整理为如下

(15)

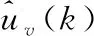
粒子群优化方法的根本思想是将优化问题的解看做粒子的位置。每个粒子在空间中以一定的速度运动，并不断更新飞行速度，直到飞达最好的位置，从而得到最优解。假设搜索空间为M维，种群中粒子个数为N个，第j个粒子在迭代k次后的速度记为

Vj(k)=(vj1，vj2，…，vjM)T

(16)

位置记为

Xj(k)=(xj1，xj2，…，xjM)T

(17)

每一次迭代中粒子的速度和位置通过下式更新

Vj(k+1)=Vj(k)+γ1j(pj-Xj(k))+γ2j(G-Xj(k))(18)

Xj(k+1)=Xj(k)+Vj(k+1)

(19)

其中，pj为第j个粒子在迭代k次后最好的位置，G为整个粒子群中最好的位置，γ是[0，1]之间满足正态分布的随机数。

本文PSO结合Hammerstein模型量化方法具体步骤如下：

1) 确定粘滞参数取值范围、延迟时间和待优化维度，并初始化粘滞参数S和J；

2) 采集控制回路数据，包括OP和PV数据；

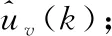
5) 通过PSO算法重复步骤3)-4)，直到均方误差VN为最小，此时对应的S和J即为粘滞量化值的估计。

5 仿真验证与工业实例

为验证上述方法的有效性和准确性，分别在仿真环境和实际工业数据环境下对其验证。

5.1 仿真验证

对于一个单输入单输出的控制回路，其控制器和被控过程对象的传递函数模型如下

(20)

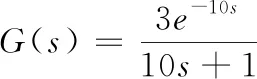
(21)

实验过程中回路输入给定单位阶跃信号，运行总时间为1000s，采样周期T为0.1s，共采集了10000组数据，为去除初始阶段采样数据的瞬间波动影响，选取最后的4096个数据进行研究。

分别对控制器参数不佳、外部振荡干扰和阀门粘滞这三种情况进行了仿真。其中，控制器比例系数P分别取0.5和0.7，分别模拟控制器在参数良好和参数不佳的情况。采集单位正弦信号作为外部干扰，其公式为x(t)=Asin(t)，A的值为1。阀门粘滞模型采用Li模型，S=0.0，J=0.0表示无粘滞，有粘滞情况分别取S=0.5，J=0.2(欠补偿情况)、S=0.5，J=0.5(无补偿情况)和S=0.3，J=0.5(过补偿情况)。在基于S，J所描述的粘滞模型中，粘滞程度的大小和S，J的大小相关。S越大，则粘滞加死区的和就越大；J越大，则粘滞越大。

表2为上述不同情况下的非线性检测结果。

表2 非线性检测结果

由表2可知，三种粘滞情况下的NGI都大于0.001且NLI大于0.01，检测结果为回路中存在阀门非线性，而控制器参数不佳和外部振荡干扰情况下的NGI均小于0.001，检测结果表明回路种回路性能下降的根源中检测出阀门非线性。

在检测出控制回路存在非线性后，为进一步确定此非线性由阀门粘滞引起。对控制器输出信号和过程输出信号进行椭圆拟合，其结果如图5所示。

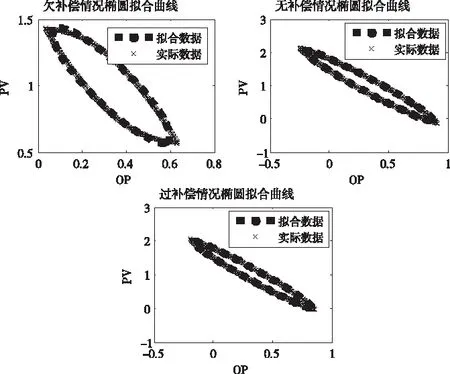
图5 粘滞情况下的椭圆拟合图

由图5可知，三种情况下的PV-OP图都产生了极限环现象，且椭圆拟合曲线和仿真数据曲线几乎一致。由此，可以判断该阀门非线性的类型为粘滞。

接着，采用本文提出的方法对上述三种不同程度粘滞进行量化估计。粘滞参数取值范围根据OP数据范围选取，待优化维度为2维，最大迭代次数设置为20次。结果见表3。

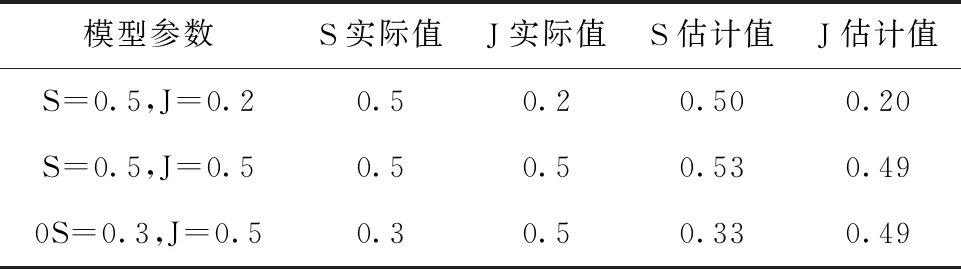
表3 粘滞量化结果

由表3可知，模型参数实际值为S=0.50、J=0.20时，估计值为S=0.50、J=0.20；模型参数实际值为S=0.50、J=0.50时，估计值为S=0.53、J=0.49；模型参数实际值为S=0.30、J=0.50时，估计值为S=0.33、J=0.49。虽然估计值和实际值并不是完全相等的，但之间的偏差是非常小的。量化结果表明了本文方法的准确性和有效性。

进一步，为了验证本文方法抗干扰能力，考虑干扰和阀门粘滞同时存在的情况。假设阀门存在粘滞的情况下同时存在方差var=0.005的高斯白噪声。在粘滞大小分别S=0.5，J=0.2、S=0.5，J=0.5和S=0.3，J=0.5时的非线性检测结果如表4所示。

表4 有噪声情况下非线性检测结果

由表4可知，回路中存在粘滞问题同时又遭受外部噪声干扰时，非高斯性指标NGI和非线性指标NLI均分别大于0.001和0.01。检测结果表明回路中存在阀门非线性。

检测出控制回路中存在阀门非线性后，为判定此非线性是由阀门粘滞引起。对OP和PV数据进行椭圆拟合，结果见图6。

图6 有噪声情况下的椭圆拟合图

由图6可知，噪声存在时仿真数据受到了一定程度的干扰，仿真数据曲线有一定的波动。但从宏观上看PV-OP图仍然表现出了极限环现象，且椭圆拟合曲线和仿真数据曲线基本重合。说明外部噪声存在时，回路中的粘滞能够被准确的检测出来。随后，再使用本文所提方法对粘滞程度进行量化，其结果见表5。

表5 有噪声情况下粘滞量化结果

由表5可知，噪声存在时粘滞的估计值和无噪声时的估计值相比有了细微的变化，但是，估计结果仍然和粘滞的真实大小很接近。从而验证了本文方法的抗干扰性。

5.2 工业实例

为进一步验证本文方法的有效性，选用了国际阀门粘滞数据库[15]控制回路CHEM6的数据。这个回路性能下降的原因已经被确定为由阀门粘滞引起。用本文所提出的粘滞检测和量化方法对此控制回路CHEM6进行测试。

由表6可知，CHEM6回路的NGI值为0.47、NLI值为2.59。将其与表1中的阀值对比可以判断回路中存在阀门非线性。确定阀门非线性后用椭圆拟合法对非线性类型进行判定，其拟合结果如图7所示。PV-OP图呈现极限环现象表明非线性的类型是粘滞。最后对粘滞的大小进行量化，由于CHEM6回路的实际阀门粘滞大小未知，将本文方法粘滞量化结果与Karra方法量化结果[16]对比。由表6可知本文方法粘滞参数S估计值为0.17、J估计值为0.20，Karra方法粘滞参数S估计值为0.20、J估计值为0.20，本文方法量化的结果和Karra方法量化结果几乎一致，从侧面验证了该方法的有效性。粘滞检测和量化结果表明CHEM6回路的阀门存在粘滞，这与实际情况是一致的。