基于物联网的农作物生长监测数据融合仿真
2021-11-17黄全高
黄全高
(赣南师范大学,江西 赣南 341000)
1 引言
农作物的生长与光照强度、温湿度、土壤的PH值等环境条件有着密不可分的联系[1],如何快捷高效地筛选并提取农作物的生长环境数据从而帮助其健康生长,将农产量大幅度提升,是实现精准农业管理的核心内容。随着网络技术的不断革新,物联网能够有效地将信息化与农业结合在一起,摒弃了传统生产管理模式的弊端,打开了现代化农业生产的新局面。
农业信息传输主要采用无线传感网络,其数据信息数量十分庞大,且网络中各个节点对数据的处理能力有限,因此对物联网中所监测的数据进行数据融合是很有必要的[2]。数据融合是一种多源信息的综合技术,可以把监测到的诸多繁琐数据进行整合使其简单化,消除干扰与噪声,同时减少数据的富裕度,提升数据采集的效率与精准度。
针对数据融合的相关问题,研究人员提出如下解决方法。蔡昱[3]等人提出一种基于WDNN网络的两级温室数据融合方法,通过构建WDNN深度学习模型,将该输出数据依据少数服从多数的方式进行融合,从而得到温室整体的评估结果,但该方法存在融合精度不高的问题。朱银锋[4]等人提出一种基于分数阶微分算子的多传感器数据融合算法,通过将周边环境的某种特性当作数据检测的影响因素,运用分数阶微积分的概念推理得到基于分数阶微分的多传感器数据融合算法模型,以此检测不同环境下的温度变化。但该算法只考虑采样数据的空间关联特质,对节点取样值是一个随机变量和取样方差对数据的影响有所疏忽,获得的结果具有较大程度的误差。
通过总结上面方法出现的问题,提出一种基于物联网的农作物生长监测数据融合方法,该方法首先对监测数据进行预处理,去除粗大误差;其次建立卡尔曼滤波模型,使得数据的噪声降到最低;最后将数据进行加权数据融合。通过仿真证明此种方法可行性较高,可以大大提升数据融合的精确性,从而对农作物的生长起到积极作用。
2 基于物联网的农作物生长监测数据融合
2.1 监测数据预处理
估计算法需要依据可靠的测量初值才能完成,在反复测量单一节点的过程中,无法确保每一次的测量值都是对的,所以先要去除粗大误差[5]。粗大误差(又称疏失误差)表示在测量时,偶尔出现的某些不应发生的异常因素导致测量数值超出正常测量误差范围的小概率误差。无线传感器网络在数据采集的过程中,因外界干扰有时会出现粗大误差。数据中若含有粗大误差,会极大程度扰乱试验结果,对试验结论的正确性也会产生影响。去除监测数据中的粗大误差,能够将数据融合的自适应度及精准度大幅度提高。最常使用的去除粗大误差方式有分布图法、拉伊达法则、格拉布斯准则等。分布图法利用中位数、四分位数等剔除粗大误差,但过程比较复杂。拉伊达法则只有在测量次数趋于无穷大时才较为适用,测量次数在有限范围内时适用性不强。
通过多次验证得出,在检测较少数据时,格拉布斯准则剔除粗大误差的准确性较高,为了确保即时性,在单位时间内对数据取样的次数不宜太频繁,因此选择格拉布斯准则去除粗大误差。
假设某个节点单位时间内的测量数据分别是x1,x2,x3,…,xi,…,xk,那么此节点测量数据算术平均值
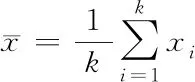
(1)
其中,Vi为第i个测量值的剩余误差。
对应的该组数值标准差为

(2)
在表1中可以查出格拉布斯统计量的临界值g0(n,α),即p[g≥g0(n,α)]=α(显著水平α一般取0.05或0.01,即置信度是94%或者98%),为提高测量精度,取置信度为94%。
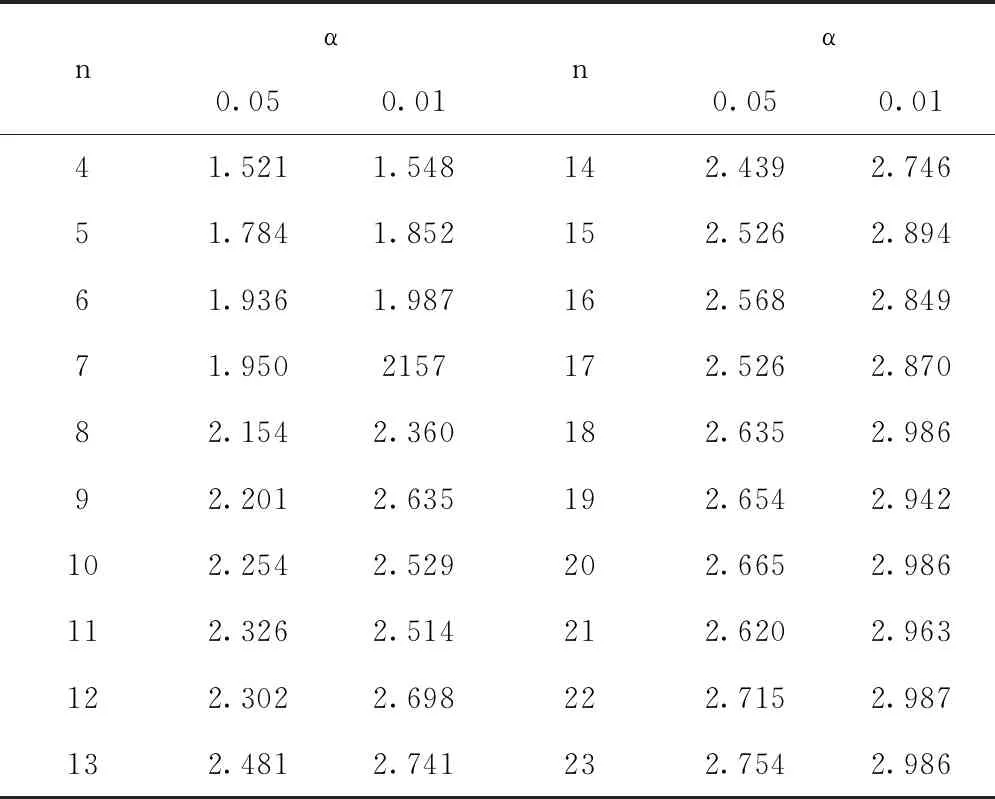
表1 部分常用格拉布斯准则临界值
如果第i个测量数据xi包含下列条件,即
|Vi|≥g0(n,α)σ
(3)
则把xi进行剔除。
把余下数据反复进行上面的过程,直到所有数据满足要求为止。
2.2 建立数据融合模型
虽然对农作物监测数据进行了预处理,提高了数据的准确率,但因为其特质及环境因素变化,在数据的采集中时常会存在数量众多的偏差存在[6]。卡尔曼滤波是一种依据最小均方误差为基准的递推无偏估计算法,其容错性能极好,能最大限度使监测的数据值与真实值更为接近,将噪声带来的影响降到最低。
卡尔曼滤波算法,需要构建一个状态空间模型,利用上一阶段的系统状态估计值与现阶段系统状态观测值,确定其中存在的过程噪声和观测噪声,来不断变换系统状态变量的估计值,使之与真实值更加相近。过程如下所示。
系统的状态方程可以表达为
X(k)=AX(k-1)+W(k)
(4)
其中X(k),X(k-1)分别是k、k-1时刻的状态值,A是状态转移矩阵,W(k)是过程噪声,W(k)~N(0,Q)。
可将过程噪声W(k)与观测噪声V(k)可看作是高斯白噪声,依照式(4)进行状态一步预测,将k-1时刻的状态X(k-1|k-1)对k时刻的预测值X(k|k-1)可以表达为
X(k|k-1)=AX(k-1|k-1)+BU(k)
(5)
U(k)是现在状态的控制量,假如无控制量的产生,可以是0。与X(k|k-1)相对应的协方差可以表达为
P(k|k-1)=AP(k|k)AT+Q
(6)
其中,P(k|k-1)代表与X(k|k-1)相对应的协方差,P(k-1|k-1)代表与X(k-1|k-1)相对应的协方差,AT是A的转置矩阵。
通过式(5)、(6)能够得出现在k时刻的系统状态最优估计值X(k|k)
X(k|k)=X(k|k-1)+Kg(k)Z(k)
(7)
其中Kg(k)是卡尔曼增益(Kalman Gain)。
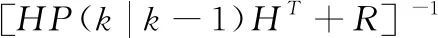
(8)
想要将所提算法滤波持续迭代运转,需将目前k时刻下X(k|k)的协方差不断进行更新
P(k|k)=[I-Kg(k)H]P(k|k-1)
(9)
其中,I代表单位阵。当系统进入下一时刻时,P(k|k)就是式(6)中的P(k-1|k-1),这样卡尔曼滤波依照如前所述的公式就能够不间断地进行自回归迭代。由此可知,卡尔曼滤波是一种在时域基础下的滤波,运算较为方便,在迭代进行时仅需保留前一时刻计算参数的变量值[7],这样可以大大减少空间存储数量,提升空间利用率。
温室状态下极易产生诸多干扰,先将监测数据采取预处理手段,然后使用卡尔曼滤波算法,把噪声影响所致的偏差值降到最低,有效实现追踪被测参变量的真实值。
2.3 多传感器数据融合算法
中心节点使用最小二乘理论下的加权数据融合。若n个传感器的观测方程是
Z=Hx+V
(10)

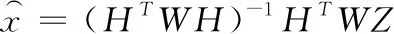
(11)
其中,zi是每个传感器的测量值,wi是其对应的加权系数。定义估计误差
(12)
其中,测量噪声V表示高斯白噪声,期望等于零。对式(12)两端在同一时刻取期望,可以得出
(13)
由式(13)能够得到,加权最小二乘法是一种无偏估计算法,该算法准确性高,优良性好。按照式(13)可得到误差的估计方差如式(14)
(14)
依据得出的估计误差数值取最小值的原则,求式(14)对wi的偏导,让其数值为零,可得出式(17)
(15)
由此可知测量方差和加权系数有直接联系。因为卡尔曼滤波对状态的真实值进行追踪监测,因此所提方法运用方差估计学习算法实现数据的加权融合,过程如下所示:
假设中心节点有n个数据要实现数据融合,xi(k)表示第i个传感器在k时刻下所显示的数据。
1)算出k时刻下任意节点状态均值,获得第i个节点k时刻的状态值和均值,最后将两者差方当成第i个节点k时刻的测量方差分配值,过程如式(16)所示
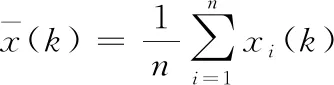
(16)

2)获取全部测量方差分配值的平均值,将其看成目前时刻测量方差数值的估计值,详细过程如式(17)所示

(17)
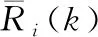
当农作物处于温室状态,传感器节点向中心节点传递信息的过程中,极易发生丢包问题,数据丢包将会大幅降低其精确率[9]。当相同节点接连发生丢包或在同一时间段簇内多个节点发生数据丢包时,可直接导致传感器稳定性变差,并且使中心节点融合数据不能如实反映温室内农作物生长的变化走向,从而导致网络性能利用率降低[10]。
通常产生数据丢包现象时也可通过传感器的历史数据取代丢包数据的方式来解决此问题。但是有持续丢包问题时,这种算法的可行性不高。本文所提方法使用状态补偿手段,采集数据的变化走势及速率,从而对数据状态进行预先推测,把状态预测值当成目前时刻丢包节点的上传数据。
若某个传感器节点k将上传数据,k+1时刻有丢包问题,过程为
δ(k)=x(k)-x(k-1)
(18)
其中,x(k-1)是k-1时刻传感器的上传数据,x(k)是k时刻传感器的上传数据,δ(k)表示在k时刻的数据增加数量,其作用是可以反馈测量数据的变化速率。当k+1时刻有丢包现象时,通过式(19)预测作为k+1时刻的状态补偿。
x(k+1)=x(k)+αδ(k)+β(δ(k)-δ(k-1))
(19)
其中,α表示速率变化系数,β表示趋势变化系数。
使用状态补偿手段来解决传感器网络数据丢包问题,能够最大程度减小数据的偏差率,使其在监测农作物生长中更具实用性。
3 仿真研究
为了验证所提方法的有效性,仿真使用的无线传感器采集数据时间间隔是3h。实验环境如图1所示。

图1 实验环境
一个传感器36h农作物生长含水量的变化曲线如图2所示。
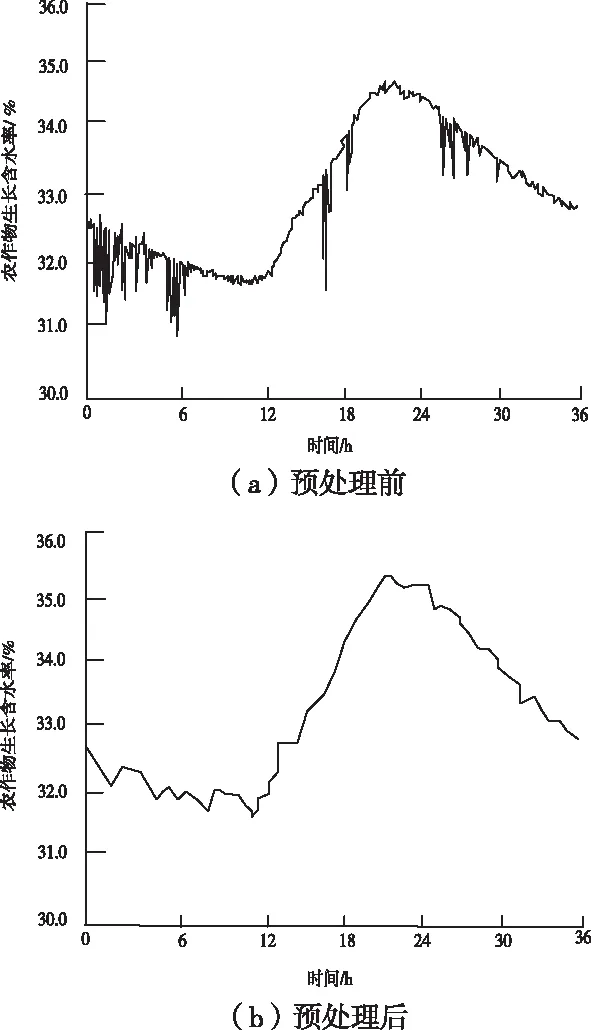
图2 预处理前后曲线示意图
如图2(a)所示,采集的数据抗干扰性很差,曲线波动较大,表明有异常数据的产生。数据采取数据预处理之后的变化示意图如图2(b)所示。通过对比图2得出如下结论:数据经过预处理之后,能够有效去除异常数据,使变化曲线更为顺滑,数据浮动波度起伏减小。在网络运转时,抗干扰能力有明显改善,更具稳定性。
在中心节点进行数据融合的过程中,本文所提方法使用状态补偿手段处理节点在传递数据时发生的丢包问题,减少误差,提升融合准确度。为了进一步验证监测数据融合准确率,所提方法与文献[3]方法、文献[4]方法对比,实验结果如图3所示。
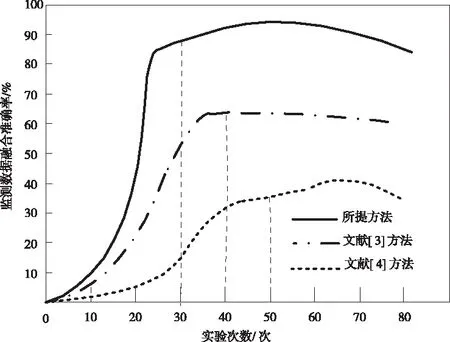
图3 监测数据融合准确率对比图
如图所示,通过观察能够得知当传感器节点传输数据的过程中,所提方法监测数据融合准确率在90%左右,相比传统方法,具有明显优势。
为了进一步验证所提方法的融合效率,以融合时间为指标,进行仿真,实验结果如图4所示。
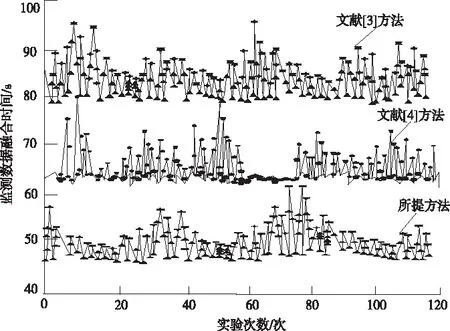
图4 不同方法融合时间对比图
如图4所示,所提方法的融合时间在53左右,短于传统方法,说明所提方法具有较高是融合效率。
4 结论
针对传统数据融合的不足之处,例如精准度不高、融合时间长等问题,提出一种基于物联网的农作物生长监测数据融合方法,所提方法主要分为三部分。首先将监测数据进行数据预处理,这样可以大大降低网络能耗,提高网络生命周期;其次通过卡尔曼滤波有效去除数据中的噪声;最后以农作物生长监测数据融合准确度和融合时间为指标进行实验。经过仿真,结论表明所提方法数据融合准确度较高,数据融合时间较短。
