一种适用无人机集群的多段补偿时间同步算法

张 然，刘春玲，程珺炜，丁元明

(大连大学信息工程学院，辽宁 大连 116622)

1 引言

随着人工智能、传感器以及通信技术的快速发展，无人机集群能够突破单个无人机在技术和性能上的限制，最大限度地发挥作战效能，对无人机集群协同作战的研究尤为重要[1，2]。无人机节点通常采用时分多址(Time Division Multiple Access，TDMA)方式接入网络，而基于TDMA的时隙分配机制必须是同步接入的，网络的各节点需要保持时隙的精确同步。时间同步技术对于提高无人机集群的网络稳定性，缩短其信息传输的响应时间，以及提高整个无人机集群网络的运行效率都具有重要意义[3]。

目前无人机集群自组网中采用的同步技术中，主要有以下几种：利用全球定位系统(Global Positioning System，GPS)时标作为时间基准；采用临时群首作为时间主控节点来实现网络时间同步；自组织网络的分布式同步技术[4-6]。目前已有不少学者提出通过调整节点时钟算法提高时间同步精度，文献[7-11]提出了一系列时间同步算法用以估算相对偏移量的关系，算法通过节点之间进行周期性的时间信息交互，然后对附近几个节点调整自身时钟收敛到一定范围，达到了网络内对节点同步精度的需求。该类同步算法可以由网络内节点分布式地去完成，而且可以降低多跳拓扑结构累计对时间同步误差的影响。网络时间的基准端若被干扰则会导致整个数据链网络瘫痪，针对这一缺点，文献[12，13]提出了数据链终端互相校准时间同步算法，该算法可以提升之前网络的抗干扰能力，而且对时间同步的收敛性能也有所提升。但是，以上的各类算法均忽略了对不同节点时钟的偏移率进行补偿及获取时间戳存在的误差问题，随着时间的推移，这些误差对时间同步的影响会逐渐增大。

因此，本文针对无人机集群网络中时间同步精度的需求，同时考虑节点高速移动及网络临时性造成网络拓扑内高动态变化的特点，提出一种适用于无人机集群的多段补偿双向时间同步算法。该算法基于均值滤波和指数平滑法来补偿时钟偏移，能有效地滤除延迟抖动以及时间戳带来的误差，且不会影响通信系统的网络开销。

2 无人机网络时间同步算法

无人机群网络中的每一个节点都必须保持着精确的时隙同步。首先将有时间戳信息的同步消息的类型及发送方式通过同步协议进行选择，再由时钟调节算法调节网络节点的本地时间。而时钟同步的精度主要取决于时钟的制作材料、时钟老化程度、协议的类型、协议的实现、网络的大小和类型以及其它外界环境因素，如湿度、温度等。因此，如何解决在无人机网络系统内各个节点之间时隙同步问题是保障时隙分配顺利完成的前提。为了保障保证通过网络互连的不同节点的本地时钟对齐，需要一种适合的时隙同步算法。

2.1 时钟模型

无人机网络虽然有中心节点为其发布同步信息，但是每个节点上的物理时钟受环境因素影响产生偏移，产生不同的时钟速率和初始时钟偏差。

网络中每一个节点都是通过对节点内部晶振输出的脉冲进行计数，从而得到本地时间。在理想情况下，节点的时钟T(t)可表示为

T(t)=t

(1)

式中t为参考时间。

然而实际情况下，第i个节点的时钟Ti(t)可表示为

Ti(t)=θi+fit

(2)

式中θi表示节点时钟偏移量，fi表示节点时钟偏移率。

时间同步过程的目的就是利用合适的算法，精确算出节点的时钟偏移量θi和时钟偏移率fi，最后进行补偿从而使得各个节点间的时间保持同步。

2.2 双向时钟同步算法

由于网络内每个节点的时间基准(Time of Day， TOD)之间存在误差是在所难免的，于是在微时隙中设置了一小段的时间为保护时间，但是随着时间的积累，产生的误差就会大于时隙中设置的保护时间。

双向时钟同步算法是一种使用双向信息交换的方式来估算和补偿传播时延的方法，这种算法的特点是参与时隙同步的节点进行双向对传，获得双方TOA，从而可以抵消掉无线信号在传输路径中所产生的误差，最后可以通过计算，从而得到精准的双方时隙误差。

针对无人机集群网络中时隙同步的主要思想是：选取网络中精度高节点的时钟作为基准时钟，询问方作为子时钟，子时钟都需要与主时钟进行时钟同步。该算法不需要基准单元必须在一个时隙内回复，不会影响高优先级业务的传输，保障业务的服务质量和消息传输的实时性。

双向时钟同步算法的整体信息交互过程如图1所示。

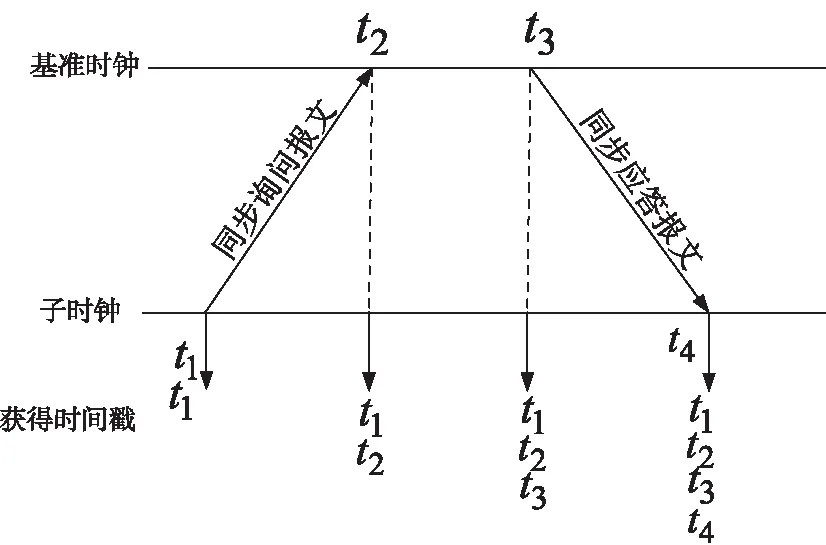
图1 双向时钟同步算法过程

双向时钟同步算法的具体步骤如下：

1)在时间同步周期到来的时候，子时钟给基准时钟发送时隙同步询问报文，并且记录下子时钟发送时的时间戳t1；

2)当基准时钟在接收到时隙同步询问报文时，基准时钟记录下此时本地时钟的时间戳t2；

3)在空闲的时隙的时候，基准时钟给子时钟回复同步应答报文，该报文中携带时间戳t2和t3；

4)当子时钟在接收到基准时钟发送同步应答报文时，子时钟记录此时本地时钟时间戳t4。

假设主时钟与从时钟之间的偏移量为θ，从时钟到主时钟的消息传输延迟为delaysf，主时钟到从时钟的消息传输延迟为delayfs，通过同步询问报文和同步应答报文可以获得的时间t1、t2、t3和t4。从而建立如下三元一次方程组

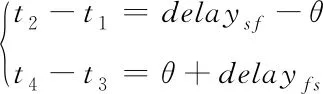
(3)

由于双向同步算法认为消息传输的链路是理想对称的，则

delay=delayfs=delaysf

(4)

可以计算出消息传输时延delay和主时钟与从时钟之间的偏移量θ，得

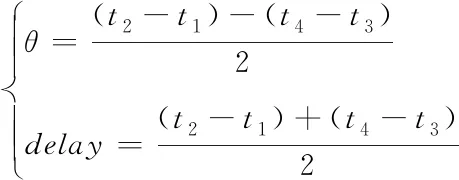
(5)

双向同步算法保障了数据链的实时服务性能，但在实际情况中由于某些因素的影响，两次信息交换无法严格遵循对称延迟。另外，该算法没有考虑环境因素对时钟偏移率的影响，导致时钟同步精度随时间变差。

3 一种多段补偿的双向同步算法

3.1 信息交换步骤的设计

针对无人机网络系统内节点高速移动及网络临时性造成网络拓扑内高动态变化的特点，同时考虑到时钟偏移率对同步精度的影响，对双向同步算法进行改进，提出一种适用于无人机集群网络的多段补偿双向同步算法，该算法的整体信息交互过程如图2所示。

图2 多段补偿双向同步算法过程

多段补偿双向时间同步算法的具体步骤如下：

1)在时间同步周期到来的时候，子时钟给基准时钟发送时隙同步询问报文，并且记录下子时钟发送时的时间戳t1；

2)当基准时钟在接收到时隙同步询问报文时，基准时钟记录下此时本地时钟的时间戳t2；

3)随后，子时钟给基准时钟发送时隙同步跟随报文，并且记录下子时钟发送跟随报文时的时间戳t3；

4)当基准时钟在接收到时隙同步跟随报文时，基准时钟记录下此时本地时钟的时间戳t4；

5)在空闲的时隙的时候，基准时钟给子时钟回复同步应答报文，该报文中携带时间戳t2、t4和t5；

6)当子时钟在接收到基准时钟发送的同步应答报文时，子时钟记录下此时本地时钟的时间戳t6。

至此，完成一次时钟同步的信息交换，并得到t1、t2、t3、t4、t5、t6这6个时间戳信息。接下来，可以根据时间戳信息，对主从时钟的时间参数进行计算。

3.2 时钟误差的计算

由于晶振漂移的影响，不同节点的时钟速率不同，即t3-t1≠t4-t2。此时，将主从时钟的频率差异定义为时间偏移率α，假设各节点的时钟速率不变，则该偏移率可以由下式计算

(6)

假设主时钟与从时钟之间偏移量θ，从主时钟的传输延迟delaysf与主从时钟的传输延迟delayfs存在delay=delayfs=delaysf，根据三次的消息发送和接受得到的时间t1、t2、t3、t4、t5和t6的值，可以建立如下方程组

(7)

根据式(7)求解得到时钟偏移量θ和传输延迟delay为

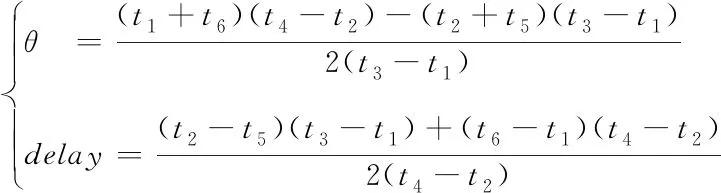
(8)

3.3 时钟漂移的预测补偿

时钟漂移随时间的变化而变化，而用于估计时钟漂移率和时钟偏移量的时间戳数据是有时效性的，通过历史样本来预测补偿下一周期的时钟偏差是一种有效的办法。考虑到从时钟所在节点的计算能力、能耗、存储容量等因素，不可能进行较大规模的数据计算和存储，所以节点的样本数据量不宜过大，且算法复杂度不宜过高。

通过式(8)得到历史最近样本为100次的数据预测并计算出的偏移率α和偏移量θ，预测下一周期时钟漂移量补偿从时钟。

在时钟晶振固定的情况下，从节点时钟在不同速率下受环境因素影响产生的是一个不随时间变化常量。故对历史样本为100次的偏移率α采取平均值滤波方式进行处理，公式如下

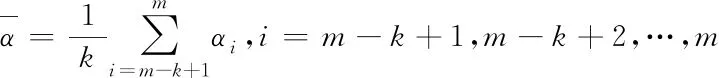
(9)

其中k=100，m为当前时刻。

考虑时钟不断漂移变化和利用数据时效性，本研究使用指数平滑法来预测时钟漂移的变化趋势。指数平滑法是一种根据经验值不断修正预测结果的一种方法，加权指数ζ通过选择最近数据加权系数衰减50%来计算得到[14]。该方法将历史样本中计算出的时钟漂移量，按照时间的先后赋予指数递减的权值然后相加得到预测值，公式如下

θi+1=ζ×θi+(1-ζ)×θi-1

=ζ×θi+(1-ζ)×[ζ×θi-1+(1-ζ)×θi-2]

⋮

=ζ×θi+ζ(1-ζ)×θi-1+ζ(1-ζ)2×θi-2+…

(10)

该方法为了能准确的反映时钟漂移的变化趋势，对时钟偏移率以及偏移量进行补偿，能在一定程度上保证预测下一周期时钟漂移量的准确性。

4 多段补偿双向同步算法仿真

4.1 仿真参数

为了验证多段补偿双向同步算法的合理性和优越性，采用MATLAB仿真软件进行仿真，并与双向同步算法进行对比分析。仿真相关参数如表1所示。

表1 仿真参数

4.2 仿真结果及分析

对双向同步算法与多段补偿双向同步算法下的时钟偏移率及偏移量进行仿真，并且对比分析不同算法下的同步精度与同步保持的效果。

1)同步精度

为了对比分析双向同步算法与多段补偿双向时间同步算法的时间同步精度，仿真了在不同的时间同步算法中，时钟偏移量和时钟偏移率与同步次数的关系，其仿真结果如图3所示。

图3 同步精度对比

由图3(a)可以看出双向同步算法与多段补偿双向时间同步算法的同步精度并没有多大的区别，两个时间同步算法最大偏移量为5us，虽然多段补偿双向同步算法比双向时间同步算法多一次信息交换，但是多出来的这一次交互是为了计算时钟偏移率，从对时钟偏移率的补偿来弥补多出来的这一次交互产生的误差。同时，可以从图3(b)看出多段补偿双向同步算法对时钟漂移的确有一定的抑制作用。这说明多段补偿双向同步算法比双向同步算法有更高的同步精度。

(2)同步保持

为了对比分析双向同步算法与多段补偿双向时间同步算法的时间同步保持性能，仿真了两种时间同步算法中，时钟偏移量和时钟偏移率与仿真时间的关系，其仿真结果如图4所示。

图4 同步保持对比

从图4(a)中可以看出，在双向时间同步算法下，随着时间的推移，时钟的偏移量不断的在累加，同步误差则越来越大，而在多段补偿双向时间同步算法下，时间偏移量的累加趋势并没有那么明显。从图4(b)中可以看出，之所以多段补偿双向时间同步算法的偏移量累加并没有像双向时间同步算法那么的快，是因为多段补偿双向时间同步算法考虑了时钟偏移率对同步保持的影响，加入了对时钟偏移率的补偿，从而抑制了偏移量的显著增加。这说明多段补偿双向时间同步算法比双向时间同步算法有更好的同步保持效果，更适用于无人机集群网络的时间同步需求。

5 总结

本研究在分析了双向时间同步算法的基础上，针对无人机群网络中的节点单元，考虑时钟偏移率对同步精度的影响，提出了一种多段补偿双向时间同步算法。通过仿真结果可知，相较于仅双向时间同步算法，多段补偿双向同步算法使得无人机集群网络中每个节点单元的主从时钟时间同步精度提高了一个数量级，同时也提高了系统同步保持性能，更适用于复杂多变的无人机集群网络的时间同步，进一步提高系统的稳定性。