融合有向D*与RRT *的移动机器人路径规划算法

刘逸凡，黄友锐，韩 涛

(安徽理工大学电气与信息工程学院，安徽 淮南 232001)

1 引言

近年来，移动机器人在自动巡检和物流运输领域的作用越发重要，是当前的一个研究热点。随着应用场景的不断增多，对机器人路径规划能力的需求也在不断提高[1]-[3]。

目前，路径规划算法主要分为两种，基于图的方法和基于采样的方法。而基于采样的路径规划算法中，应用范围最广的是快速随机树[4]-[6](Rapidly-exploring Random Tree， RRT)法，它是使用随机采样来避免构建状态空间。

文献[4]提出了RRT算法，它以起点为根进行生长，当树枝生长到目标点后，形成最终路径。文献[7]提出RRT-Connect算法，以双树形式形成路径。RRT算法对于解决单查询规划问题有着特有的优势，特别是，需要避过大量障碍物后才能到达目标地时。但由于没有考虑最优性问题，所以只能产生可行路径，却无法得到渐进最优路径。

文献[8]提出的RRT*算法，它以RRT方法找到第一个可行路径之后，会通过重新布线来优化树的结构，来返回一个更优的路径。文献[9]将RRT-Connect与RRT*相结合，提出了RRT*-Connect算法，它是能返回渐进最优解的双树算法。算法会在整个状态空间持续采样，以便返返回一个渐进最优解，但是在整个状态空间随机采样，依然不能有效的降低寻找最优路径的成本。文献[10]提出了Informed-RRT*算法，该算法在找到第一条可行路径之后，在椭圆集中进行采样来优化路径。文献[11]提出了Batch Informed Trees (BIT*)算法，通过采样和试探法交替进行来解决路径规划问题。文献[12]提出了改进RRT*FN算法，使用启发式采样方法，保留树中的高性能节点，提高了算法性能。但是这些算法在通过狭窄通道或通过连续的小洞时，仍需要大量迭代才能到达目标点。而且上述算法，只能在固定的半径范围内重新布线。当重新布线半径较小时，生成的路径中会存在大量的冗余拐点，无法满足机器人或智能车辆的运动需求；当重布线的半径较大时，采样点的替代父节点过多，会严重拖累运算速度。

针对上述问题，本文提出了融合有向D*[13]与RRT*的路径规划算法。本文将RRT*算法的重现布线部分进行优化，在Informed椭圆集的基础上，根据有向D*的关键点思想提出了一种关键点采样集合的方法。在融合改进算法找到第一条可行路径之后，通过判断可行路径与障碍物顶点之间的距离，将部分障碍物顶点作为关键点，并以关键点为圆心，建立圆形子集。把重现布线的采样点按概率分配在圆形子集和整个状态空间中，优化转弯处的路径。再引入变距离重新布线方法，经过少量的大半径重新布线后减少冗余节点，然后利用小半径重新布线多次优化转弯处的路径，在不影响运算速度的前提下，得到一条更为平滑的渐进最优路径。本文算法在路径节点数量、路径长度等方面的有效性。

2 相关工作

2.1 Informed-RRT*算法

RRT*算法是通过在自由空间中随机采样，构成一个从起点xstart开始寻找可行路径的过程。在迭代过程中，以固定步长选取采样点方向上的新节点，直到到达目标点xgoal。

Informed-RRT*开始时与RRT*算法一致，但是在找到首条可行路径之后，会在椭球子集上继续采样，根据新添加到树上的状态进行重新布线。新添加的状态将树中附近现有节点视为替代父级，将代价最小的节点作为新的父节点，在树上形成新的树枝。

2.2 有向D*算法

有向D*算法采用反向搜索方式。从终点开始，对于关键节点采用由父节点逐级确定子节点的方式，再通过方向函数将两个节点连接成直线，判断直线与障碍物是否发生碰撞，决定该节点的去留，实现对关键节点的筛选。有向D*算法使用关键点搜索替代了传统D*算法遍历栅格状态，形成从起点指向终点的指针的搜索方式。

如图1，是有向D*算法的搜索方式，图中点S(黑色)、G(红色)分别是起点和终点，10个红色菱形是在障碍物顶点中选取的关键点。有向D*算法，对于存在障碍物的地图进行最优路径搜索时，只需要考虑对10个关键点进行访问，有效提高搜索效率。

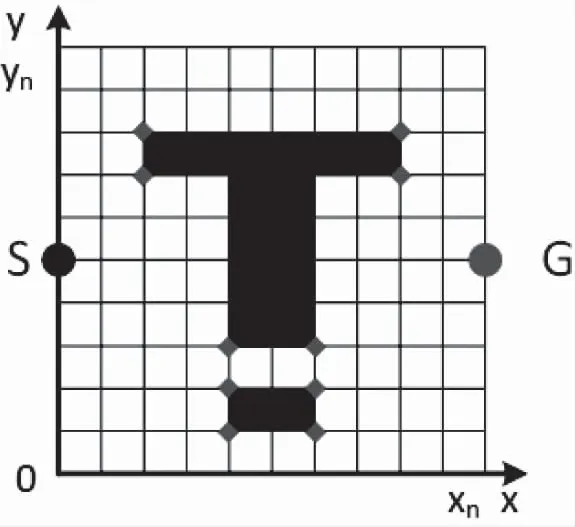
图1 有向D*算法搜索方式

3 融合有向D*与RRT*的路径规划算法

3.1 关键点的选择与概率采样

融合改进算法在搜索路径之前，首先将障碍物膨化γ单位长度，防止生成的路径与障碍物之间空隙过小，导致机器人无法顺利通过。然后使用与Informed-RRT*相同的方式，在无障碍空间内进行随机采样，以搜索节点。

在形成初始路径之后，结合有向D*算法的思想确定采样空间。将障碍物的部分顶点确认为关键点，再根据关键点确定合适的采样空间。算法从终点开始对所形成的初始路径集合S={S1，S2，…，Sn-1，Sn}进行直线化处理，其中S1为起点Xstart，Sn为起点Xgoal。首先以S1为父节点，Sn-1为子节点，两点相连，判断SnSn-1是否与障碍物发生碰撞；若没有碰撞，则将Sn-2设为子节点，再次判断SnSn-2是否与障碍物碰撞；进行顺序比较，直到SnSk与障碍物发生碰撞，此时把父节点Sn的位置信息存入OPEN列表中，再把Sk设为新的父节点，Sk-1设为子节点，判断SkSk-1是否与障碍物发生碰撞，按顺序将发生碰撞的父节点存入OPEN列表中，直到将S1选为子节点，停止判断，将S1存入OPEN列表。将OPEN列表中的所有节点依次连接，形成优化后的最初路径。若障碍物顶点与优化路径距离小于3个单位长度，就将其选择关键点并形成关键点集合X={X1，X2，…，Xn}。

最后以关键点X为圆形，δ为半径，形成数个圆形子集作为采样空间。每次采样情况可用式(1)表示，其中s为调用函数生成的浮点数，sr为目标采样概率，sample_c和sample_o分别表示算法在圆形采样空间内采样和在整个无障碍空间内采样。

(1)

本文算法的圆形采样子集与优化后初始路径如图2所示。

图2 圆形采样子集示意图

图中，Xstart和Xgoal分别表示起点和终点。因为黑色障碍物顶点v与初始路径之间的距离小于D，所以将膨胀处理后的新障碍物中对应的顶点v’设为圆心，δ为半径形成圆形采样子集(蓝色虚线)。

3.2 变距离重新布线

采样后产生一个随机点Xrand，以Xrand为圆形，r为半径，在树上搜索节点，将搜索到的相邻节点形成集合Xnear。cost()是指从树的起始节点到本节点的路径代价。cost(L)是指从相邻节点到到新产生的节点Xrand的路径代价。算法没有将距离采样点最近的节点作为父节点，而是选择到采样点Xrand路径代价最小的节点，判断公式如下：

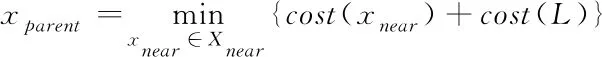
(2)

将每个相邻节点进行比较，选择路径长度最优的父节点。如果在无碰撞情况下，存在路径代价更小的节点，就将其定义为Xrand新的父节点，当在搜索范围内得到路径代价最小的父节点时，便将这条路径作为新生成的树枝添加到树中。

在进行半径为r的搜索时，r为一个变量，它会随迭代次数的增大而不断减小，表示为

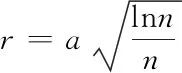
(3)

式中，n为当前的迭代次数，a是根据地图大小而确定的常量。

3.3 算法实现流程

算法流程图如图3所示。

图3 本文算法流程图

融合改进算法实现步骤如下：

步骤1：初始化参数，将路径规划起点Xstart作为随机树T的根节点。迭代开始，使用RRT算法在无碰撞障碍空间进行均匀采样，直到生成第一条可用的初始路径；

步骤2：将形成的初始路径节点存入集合S={S1，S2，…，Sn-1，Sn}，以Sn为初始节点的父节点Sp，Sn-1为初始子节点Sc。

步骤3：将父子节点相连，判断两点连线是否与障碍物发生碰撞，若SpSc与障碍物未发生碰撞，就将Sc-1作为新的子节点，重复步骤3，若SpSc与障碍物发生碰撞，就将Sp存入OPEN列表中，把子节点Sc设为新的父节点Sp，将Sc-1设为新子节点Sc；

步骤4：判断子节点Sc是否为路径起点S1，如果不是路径起点，就重复步骤3，若Sc是路径起点S1，就将OPEN列表中的点依次相连，形成优化后的初始路径；

步骤5：将所有障碍物膨化γ单位长度，原障碍物的顶点为v，膨化后的障碍物对应顶点为v’，若顶点v和优化后的初始路径之间的距离小于单位长度a，就把顶点v对应的v’设为关键点，再以关键点为圆心，δ为半径形成圆形采样区域；

步骤6：随机生成一个0-1的浮点数，判断是否大于目标采样概率sr，当大于sr时，本文算法在圆心区域内进行均匀采样，若小于sr，则在所有的无碰撞区域内均匀采样；

步骤7：以采样点为圆形，r为半径，搜索相邻节点，计算从路径起点到相邻节点再到采样点的路径代价，通过式(2)筛选出采样点的父节点再将两者相连，将新点和生成的树枝加入到树中；

步骤8：判断迭代次数n是否达到预设值，若小于预设值，则重复步骤6，若迭代次数到达上限，就将Xgoal加入到树中，从Xgoal回溯到起点Xstart，得到最终路径。

4 仿真与分析

为了验证融合有向D*与RRT*的路径规划算法(DDS-RRT*)的有效性，分别在不同环境中，将RRT*算法、Informed-RRT*算法、RRT*-Connect算法、BIT(batch_informed_trees)算法以及本文提出的DDS-RRT*算法在Python3.7中进行对比。给出DDS-RRT*算法的生长结果和五种算法的最优路径结果，并且对机器人行驶的路程、时间和总步数进行比较和分析。在仿真中对障碍物进行膨化处理，并将机器人视为一个点。由于RRT类算法具有随机性，所以在每张地图中都进行40次独立实验，最大步长为2，最大迭代次数为8000。

4.1 地图1中的仿真

地图1(50×30)中起点和目标点设置为(5，5)，(45，25)，用来模拟存在随机稠密障碍物的环境。在地图1中进行的仿真，如图4所示。

图4 地图1的仿真结果

图4(b)中绿色点虚线、黑色长虚线、青色长虚线、蓝色点划线和红色实线分别对应RRT*、Informed-RRT*、RRT*-Connect、BIT和本文算法，将五种RRT类算法进行40次重复实验，去除两次最优和最次结果后，五种算法的路径长度、搜索时间和总步数统计见表1。

表1 地图1中的仿真数据

五种算法迭代次数与路径长度的关系如图5所示。

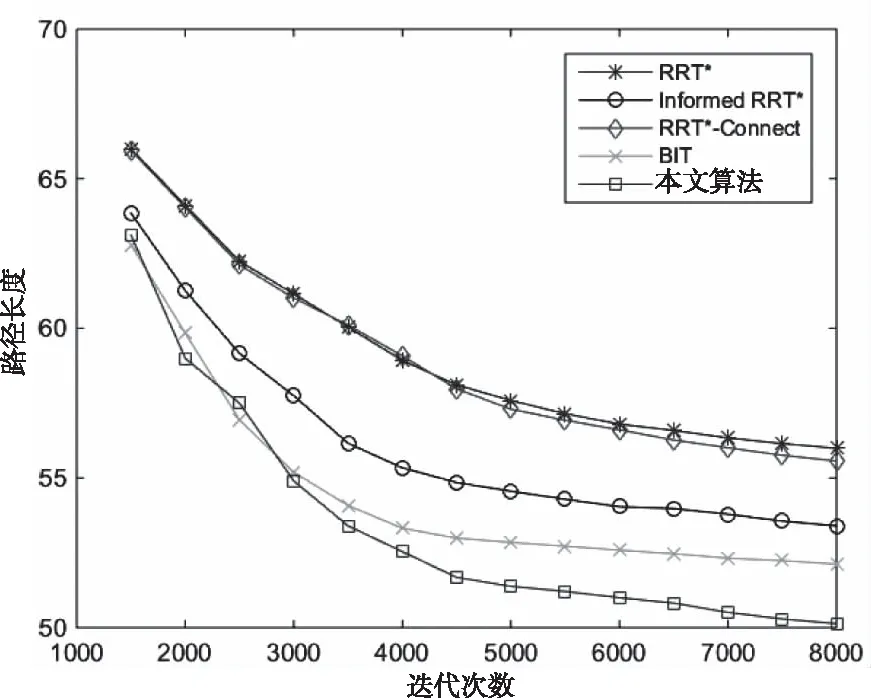
图5 地图1中五种算法路径长度与迭代次数的关系

在复杂障碍物环境中BIT是对比算法中效果最好的算法。而Informed-RRT*算法搜索时间较长，RRT*-Connect是RRT*算法的双树版本，仅在搜索时间上有较大优化，其搜索时间虽优于RRT*算法，但任弱于BIT算法。上述两种算法在地图1中的路径长度与BIT算法任差距较大。将本文算法与BIT算法比较可知，本文算法搜索时间比BIT算法减少14%，路径长度缩短了3.82%，总步数减少了58.82%。

与本文算法相比，四种对比算法不但路径收敛性较差，而且无效转弯较多，不能很好的满足移动机器人的运动需求。四种对比算法更倾向于从中间障碍物较多的区域进行绕行而不是穿过，这也增加了路径的长度。本文算法通过关键点采样方法，在复杂障碍物环境中得到的路径长度是五种算法中最优的。又因为本文算法使用了变距离重新布线策略，不但在搜索时间上比BIT算法略少，而且少量大半径重新布线，删除了树枝上大量的冗余节点。保留的高效节点使生成的最终路径上无效弯曲更少，减少了总步数，提高了路径的平滑度。五种算法生成的路径长度都随迭代次数的增大而减小并最终趋于稳定，但本文算法随着迭代次数的变化，总能提供相比其它四种算法更短的路径，并能以较小的迭代次数得到比其它算法更短的路径。

4.2 地图2中的仿真

地图2(50×30)中起点和目标点设置为(5，5)，(45，25)。与地图1相比，地图2主要是模拟迷宫环境，用来验证算法通过连续小洞的能力。在地图2中进行的仿真如图6所示。

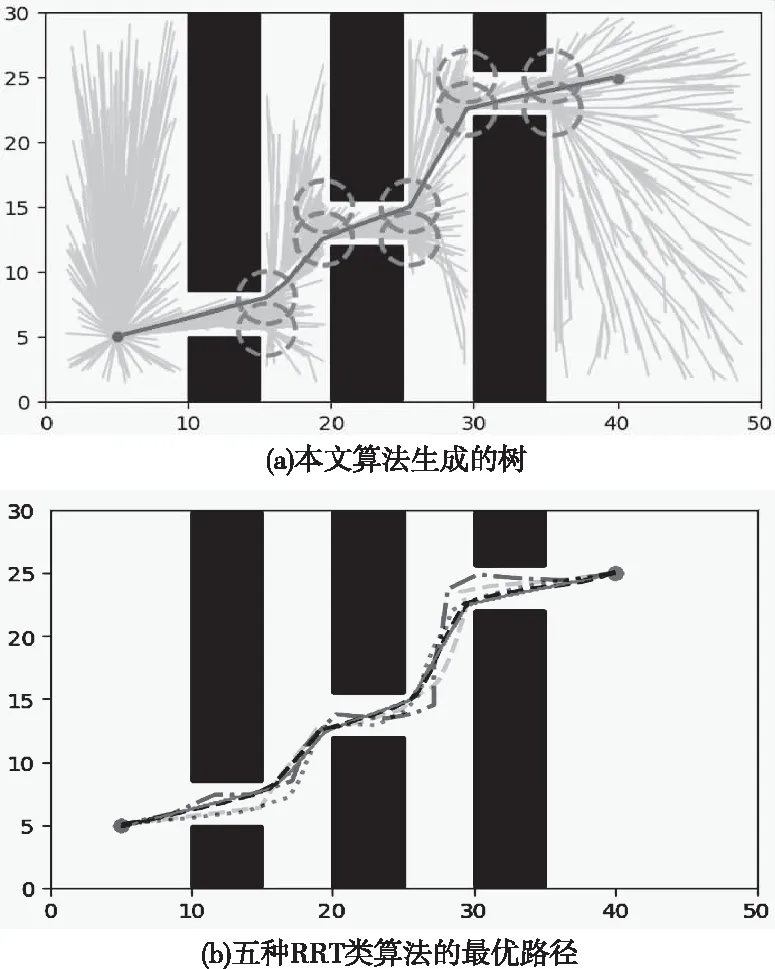
图6 地图2的仿真结果

图6(b)中绿色点虚线、黑色长虚线、青色长虚线、蓝色点划线和红色实线分别对应RRT*、Informed-RRT*、RRT*-Connect、BIT和本文算法，将五种RRT类算法进行40次重复实验，去除两次最优和最次结果后，五种算法的路径长度、搜索时间和总步数统计见表2。

表2 地图2中的仿真数据

五种算法迭代次数与路径长度的关系如图5所示。

图7 地图2中五种算法路径长度与迭代次数的关系

在地图2这种连续钻小洞的情况下，对比算法中BIT的路径成本最大，Informed-RRT*算法搜索用时最长。RRT*和RRT*-Connect算法在路径长度上较优，而且RRT*-Connect是对比算法中搜索时间最短的。将本文算法与RRT*-Connect算法进行比较可知，本文算法搜索时间减少了4.2%，路径长度缩短了5.26%，总步长减少了48.48%。

本文算法在路径长度方面是最优的，而在地图1中表现较好的BIT算法，在地图2中路径收敛性最差。五种算法相比，本文算法平均搜索时间优于RRT*-Connect和BIT算法，路径的总步长得到了大幅度的减少，路径长度也是最优的。对比五种算法在地图2中生成的路径，可以看出本文算法相比其余四种算法在障碍物顶点处的转弯更为平滑，没有出现其余四种算法中90°急转弯的情况，更加符合移动机器人的运动学规律。虽然地图2中起点和终点之间的欧几里得距离较近，但因为存在连续的狭窄小洞，增加了状态空间中无效的采样点数量，使最终的路径长度增大。本文算法与其它四种RRT类算法相比，将采样点按概率分配在障碍物顶点的圆形采样区域和整个状态空间，克服了采样点过于分散的问题，使得采样效率大大增加。变距离布线策略删除路径上的大量的无效节点，在减小总步数的同时提高了路径的平滑度。而且本文算法相比其它四种算法收敛速度更快，可以用更小的迭代次数得到更短的路径。

4.3 地图3中的仿真

地图3(35×10)中起点和目标点设置为(2，2)，(30，8)，用来模拟连续狭窄通道，验证算法在狭窄通道环境下的规划能力。在地图3中进行的仿真如图8所示。

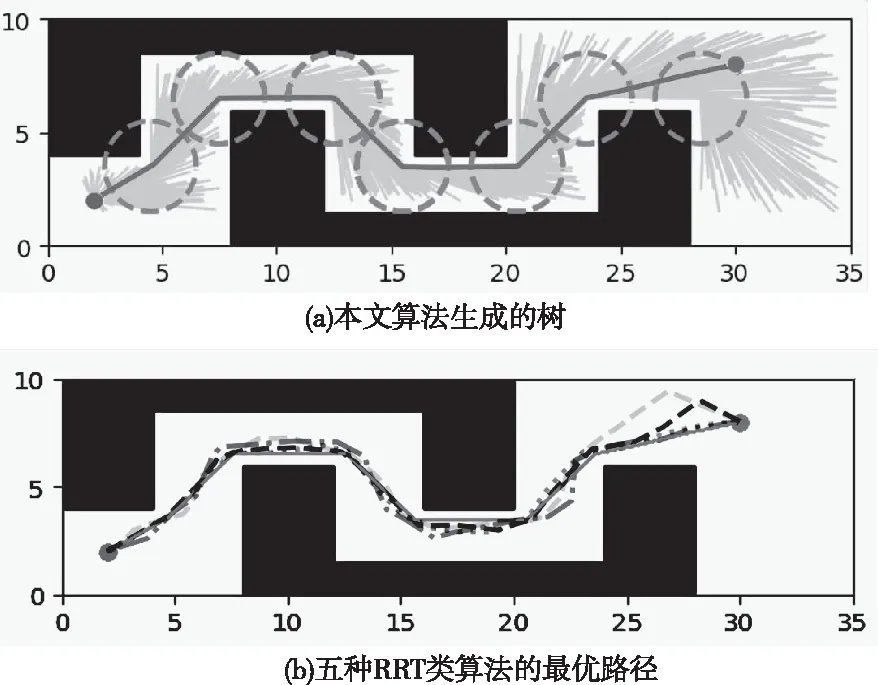
图8 地图3的仿真结果

图8(b)中绿色点虚线、黑色长虚线、青色长虚线、蓝色点划线和红色实线分别对应RRT*、Informed-RRT*、RRT*-Connect、BIT和本文算法，将五种RRT类算法进行40次重复实验，去除两次最优和最次结果后，五种算法的路径长度、搜索时间和总步数统计见表3。

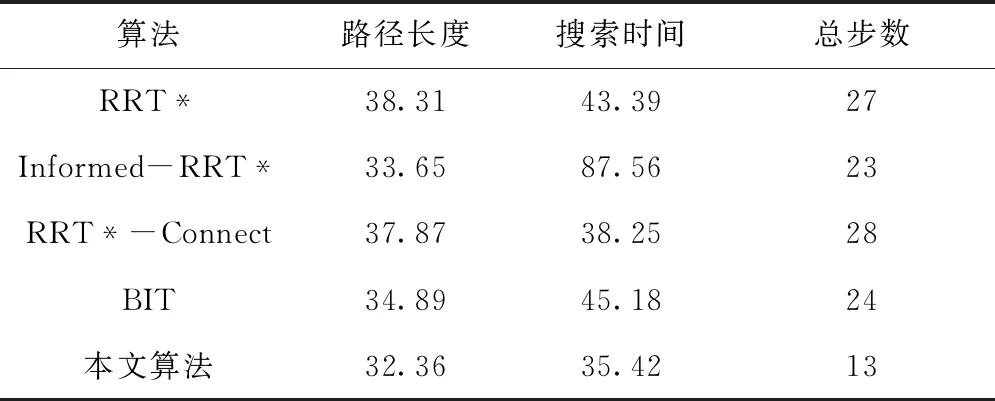
表3 地图3中的仿真数据

五种算法所生成的最优路径长度与迭代次数的关系如图9所示。

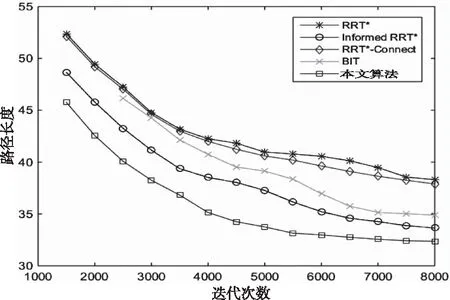
图9 地图3中五种算法路径长度与迭代次数的关系

在地图3这种连续狭小通道情况下，Informed-RRT*算法是四种对比算法中路径收敛性最优的，但Informed-RRT*算法搜索时间较长。本文算法比Informed-RRT*算法路径长度缩短了3.83%，搜索时间减少了59.54%，总步数减少了43.47%。对比五种算法生成的路径可知，本文算法的路径收敛性最优，且路径上的冗余拐点也更少，在通过连续狭窄通道之后，其余四种算法都发生不同程度的无效转弯，而本文算法可以用较为平滑的路径直接与目标点相连，减少了冗余路径。该算法用更少的迭代次数实现了与其它算法相同的效果，减少了搜索时间。虽然地图3中起点与终点的欧几里得距离较近，但是连续的狭窄通道放大了起点与终点之间的距离，导致Informed-RRT*算法的椭圆子集变大，影响采样效率，使搜索时间变长。本文算法的关键点采样方法在连续狭小通道内效果明显，能克服椭圆子集过大的问题，生成代价更小、总步数更少的最优路径。

5 结论

现有的RRT类算法在复杂环境中存在路径收敛性差和总步数多的问题，提出了一种融合有向D*与RRT*的路径规划算法。该算法通过关键点采样和变距离重新布线对路径规划的采样区域进行优化，减少了无用采样，提高路径规划效率。实验结果表明，本文算法在相同环境下，比四种RRT类算法的路径长度缩短了4.30%，搜索时间减少了25.91%，路径总步数减少了50.26%，且可以适应存在连续小洞和狭窄通道的特殊环境。本文算法在路径规划的收敛性和平滑性方面都有较好的效果，可以适应各种复杂环境，希望后续的研究可以将算法应用到无人机等高维度路径规划领域。