基于改进遗传算法的装备保障效能评估指标约简
2021-11-17潘成胜杜秀丽吕亚娜
潘成胜,周 敏,杜秀丽,吕亚娜
(大连大学通信与网络重点实验室,辽宁 大连 116622)
1 引言
装备保障系统效能评估以装备保障理论与系统评估理论为基础,通过多种技术对装备保障系统指挥、维修、供应等效能进行综合评价,是对装备保障系统效能的计算度量[1],不仅可以综合反映装备保障系统的组成要素、运行机制等情况[2],而且对保障资源合理配置、保障系统优化设计等具有重要指导作用,已成为一项重要而紧迫的任务[3]。
装备保障系统组织规模庞大、结构复杂,其效能评估指标繁多且相互联系、相互冗余[4],直接使用这些评估指标会导致评估模型维数较高、求解困难、评估效率低等问题。因此,研究装备保障系统效能评估指标约简意义重大。
杨志远等[5]以主动雷达导引头干扰效能评估指标体系为研究对象,采用粗糙集理论对指标体系进行属性约简。杜锋等[6]通过验证各评价指标相对于决策属性是否必要以及各子集组合相对于决策属性是否独立,对装备保障指挥系统效能评估指标体系进行约简。Wang等[7]利用粗糙集理论与灰色关联分析法对评估指标进行筛选,不仅保留了关键指标,而且允许指标相互独立。Xu等[8]应用粗糙集属性约简算法对雷达干扰效能评估指标体系进行约简,删除了冗余属性。上述方法主要基于粗糙集理论进行指标约简,但是该方法属于NP完全问题,其分明矩阵的构建过程复杂度较高,无法适应大数据量下的指标约简工作。宋佳成等[9]针对反导预警雷达效能评估指标体系中存在信息重叠问题,采用灰色关联分析理论对指标体系进行约简。该方法需要对各项指标的最优值进行现行确定,主观性过强,同时部分指标最优值难以确定,收敛性较差。
遗传算法[10]是一类可以用于复杂系统优化的搜索算法,鲁棒性较强且收敛性好。然而,传统的遗传算法(Standard Genetic Algorithm, SGA)在交叉和变异时采用固定概率进行求解,当选取的概率较大时,会破坏种群稳定性,使算法沦为随机搜索,较小时算法容易陷入局部极值,降低优化效率[11]。针对传统遗传算法存在的问题,较多学者提出了自适应机制,在算法搜索过程中动态调整交叉概率与变异概率。Sriniva等[12]提出了自适应遗传算法(Adaptive Genetic Algorithm, AGA),该算法中交叉概率与变异概率随着种群适应度进行线性调整,但该算法在初期易陷入局部极值,难以找到全局最优解。杨从锐等[13]提出了一种非线性自适应调节交叉概率与变异概率的自适应遗传算法(Improve Adaptive Genetic Algorithm, IAGA),但是该算法没有考虑种群大部分的个体适应度较小而只有少数个体适应度大的情况。金立兵等[14]提出了一种基于Sigmoid函数曲线的非线性自适应遗传算法,但该算法在进化初期变异概率过大,可能会使得算法收敛性能降低。
基于以上分析,本文提出一种基于改进遗传算法的装备保障系统效能评估指标约简方法。该方法首先对遗传算法进行改进,以强精英参与、完备交叉、预变异策略完成遗传算法的选择、交叉与变异操作;然后将改进后的遗传算法用于装备保障系统效能评估指标约简,以利用更少指标得到更高的评估精度。
2 装备保障系统效能评估指标体系构建
本文遵循完备性、目的性、客观性、层次性等指标体系设计原则[15],结合装备保障自身特性,建立装备保障系统效能评估指标体系,其构建步骤如图1所示。

图1 装备保障系统指标体系构建流程示意图
1)分析装备保障系统,得到效能指标构成体系;
2)分析装备保障影响因素,从中筛选出影响装备保障效能的主要因素;
3)以效能指标为源头,对各效能指标进行层次分解,构造评估指标体系的递阶层次结构,即树型结构;
4)选取与装备保障效能评估的相关属性指标,描述装备保障效能评估指标体系中个指标的含义,建立能够全面衡量装备保障系统效能的评估指标体系。
基于上述分析,构建的效能评估指标体系如图2所示。

图2 装备保障系统效能评估指标体系
3 基于改进遗传算法的装备保障系统效能评估指标约简
3.1 完备交叉与预变异
遗传算法模拟自然界优胜劣汰的进化现象,将待优化问题解集的搜索空间映射为遗传空间,根据适应度值进行选择、交叉与变异操作,完成种群进化过程,最终获取最优解。其中,交叉操作主要对遗传空间进行探索,通过对父代个体进行交叉操作以产生新个体;变异操作是遗传算法中的辅助性搜索操作,其主要目的是通过变异算子找到新基因,以维持种群多样性,使算法跳出局部最优解。上述操作是遗传算法的关键所在,直接影响算法性能。
1)交叉、变异问题分析
SGA算法采用固定值的交叉概率与变异概率,该方法虽然使得算法简单易行,但是容易陷入局部最优解,且算法收敛性较差。针对上述问题,较多学者提出了各种自适应遗传算法。在算法初期,使用较大的交叉概率与较小的变异概率,促进种群进化,加快算法收敛速度;算法运行到后期,使用较小的交叉概率与较大的变异概率,以维持种群多样性,跳出局部最优解,其交叉概率与变异概率按式(1)[16]进行自适应调整
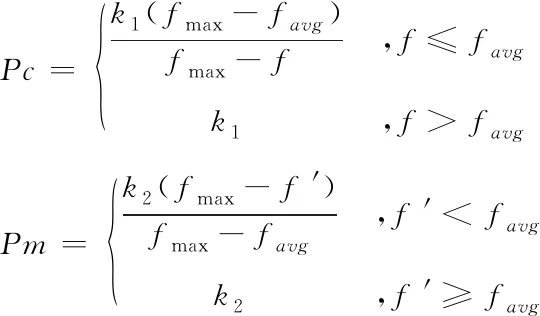
(1)
其中,fmax表示种群最大适应度值,favg表示种群平均适应度值,f表示交叉个体中较大的适应度值,f′表示变异个体适应度值。
虽然现有自适应遗传算法在收敛速度与精度方面有了一定提高,但是多数自适应算法根据适应度值动态调整交叉与变异概率,难以控制这两个概率的平衡点,且当个体适应度值高于种群平均适应度值时,自适应遗传算法处理方式较为单一,算法后期存在收敛速度慢等缺点。基于上述分析,本文通过完备交叉与预变异操作来避免以上问题。
2)完备交叉操作
完备交叉操作的基本思想:在遗传算法种群中,不论是“优良”个体还是“劣质”个体,其附近都可能存在优质解,因此,本文认为在当前代种群中,所有的个体都应该进行交叉操作,以保证新产生的个体不会遗漏优质解。因此将父代个体通过均匀交叉算法进行两两交叉,得到备选子代个体。
3)预变异操作
预变异操作的基本思想:将父代个体与备选子代分别通过单点变异算法进行预变异,得到预变异个体,对父代个体与预变异个体的适应度值以及备选子代个体与预变异个体的适应度值进行求解,当预变异个体的适应度值大于其自身适应度值时,则意味着该个体的变异操作是有效的,产生变异个体,否则该个体的变异操作是无效的,不产生变异个体。最后,将通过完备交叉与预变异操作后的个体进行适应度值排序,得到下一代个体。
基于上述思想,本文提出一种基于预变异与完备交叉的遗传算法(Genetic algorithm based on pre-mutation and complete crossover, PMCCGA)。
3.2 基于遗传算法的装备保障系统效能评估指标约简算法
装备保障系统指标繁多,直接通过这些指标进行效能评估求解复杂度高且求解误差较大,通过指标约简可以有效提高效能评估的速度与精度。本文首先采用完备交叉与预变异策略对遗传算法中的交叉与变异操作进行改进,通过综合互信息与选择比例构造算法适应度函数,然后将改进后的遗传算法用于装备保障系统效能评估指标约简,提高装备保障系统效能评估精确度。
基于改进遗传算法的装备保障系统效能评估指标约简算法步骤如下:
1)装备保障系统效能评估指标编码
本文采用二进制编码方式,用0和1表示未选中指标和选中指标。假设某装备保障系统效能评估数据集Ω中,有n个样本,每个样本有m个效能评估指标和1个评估等级标签,将评估等级划分为k级,则每个样本可以表示为Xi={xi1,xi2,…,xim,labeli},i=1,2,…,n,其中xij表示第i个样本第j个效能评估指标值,labeli表示第i个样本的效能评估等级,则用一个长度为m的0和1字符串来表示效能评估指标组合G=(g1,g2,…,gm),其中gi=0表示该效能评估指标被丢弃,gi=1表示该效能评估指标被选中。
2)遗传算法初始化
设置种群规模、最大迭代次数以及产生初始种群。
3)计算适应度函数
本文将综合互信息以及选择比例作为遗传算法适应度函数,要求综合互信息值尽可能大,选择比例尽可能小。根据以上分析,可知在进行装备保障系统效能评估指标系统约简时有两个优化目标:1)最大化综合互信息值;2)最小化选择比例。
优化第一个目标,可以建立如式(2)的目标函数

(2)
式中,n表示已选装备保障系统效能评估指标个数,Xi、Xk表示n个评估指标中的第i和第k个(i≠k)指标,Y表示装备保障系统效能评估等级,参数α、β为调节参数,α,β∈[0,1]。上式第1项为所有已选效能评估指标与效能评估等级之间的互信息和,第2项为已选效能评估指标之间的互信息,第3项为在评估等级已知的条件下,已选效能评估指标之间的条件互信息。
优化第二个目标,可以建立如式(3)所示的目标函数,该式表示已选效能评估指标个数占总效能评估指标个数的比例值。

(3)
其中,k表示装备保障系统效能评估指标体系中已选指标个数,m表示总指标个数。
将式(2)、(3)结合,建立式如式(4)所示的综合目标函数,通过优化综合目标函数能够同时优化两个目标。
F=α1f1-α2f2,α1+α2=1
(4)
α1、α2是调节参数,用来调整互信息与所选指标个数的相对重要程度。由于F函数的取值范围较小,不同个体对应的目标函数值差异可能很小,遗传算法在进行选择操作时不能有效的将适应度值高的个体选择出来,从而影响遗传算法的收敛速度与寻优结果。因此需要对F函数进行放大处理,本文采用指数函数的方法。
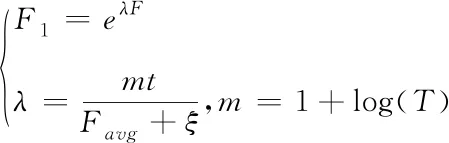
(5)
其中,λ为放大差异参数,是一个随进化代数增加而逐渐增加的动态变化的数,t为当前的进化代数,T为最大迭代次数,Favg是当前种群平均适应度值,ξ是一个足够小的数,防止分母为0。
4)判断是否达到最大迭代次数,若是,则输出当前的最优效能评估指标子集,否则执行以下步骤。
5)执行选择操作
将父代个体与子代个体按照适应度值大小进行排序,选择适应度值大的个体进入下一次迭代运算。
6)执行交叉操作
将所有的父代个体进行均匀交叉产生备选子代个体,并计算备选子代个体适应度值。
7)执行预变异操作
将所有父代个体与备选子代个体通过单点变异操作进行预变异,然后计算预变异个体适应度值,若预变异个体适应度值大于当前个体适应度值,则产生变异,否则不进行变异操作。
8)返回步骤4)。
4 仿真分析
为了验证本文所提算法的有效性,按照图3所示的仿真方案流程进行仿真。仿真中用到的Wine、Parkinsons和BreastCancer数据集为UCI公开数据集,装备保障效能评估指标数据集(Equipment Support System Effectiveness Evaluation Index data set,ESSEEI)则是通过相关调研获得,实验数据集如表1所示。
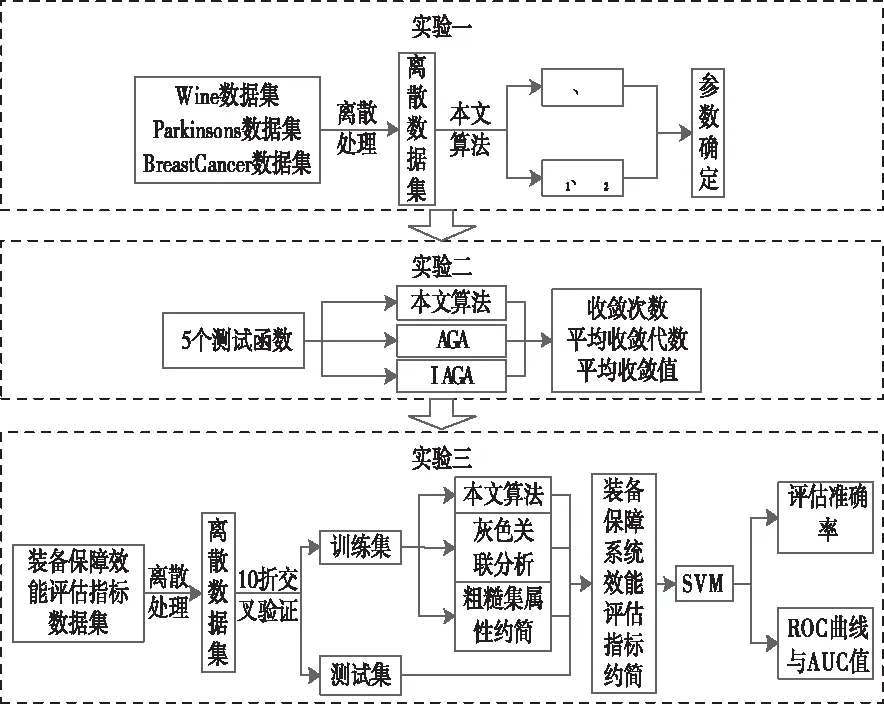
图3 仿真方案流程示意图
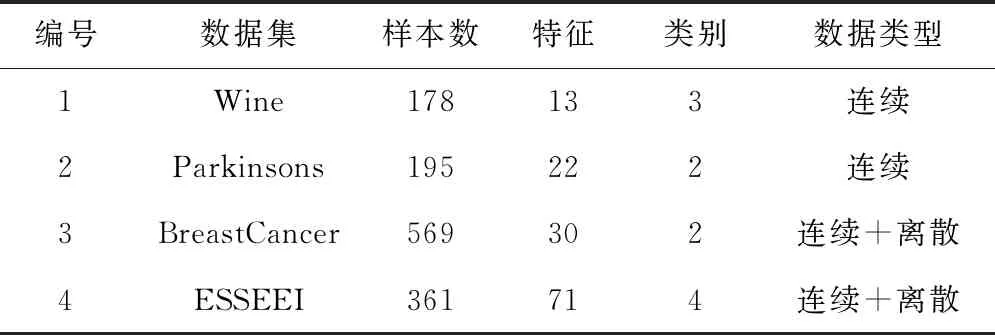
表1 实验数据集
在本文算法中,不同参数的选取会影响算法的收敛性能与寻优精度。因此,本文将通过实验一确定参数的合理取值。实验一通过控制变量法对α、β、α1、α2的取值进行仿真,仿真结果如图4所示。
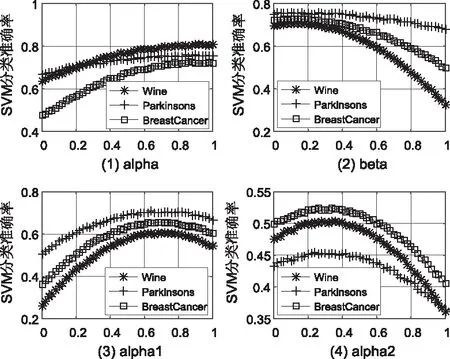
图4 α、β、α1、α2取值仿真曲线
从图4的仿真结果可以得到,当α=0.9、β=0.1、α1=0.7、α2=0.3时,SVM分类准确率最高。
实验二主要用来验证改进后遗传算法的性能,选取5个复杂函数作为测试工具,将改进后的遗传算法与AGA、IAGA进行比较验证。
f1=xsin(10πx)+2.0,x∈[-1,2]
(6)
式(6)函数是一元多峰值函数,其函数图像如图5所示,在函数定义域内,该函数存在多个极大值,其全局最大值为3.8503,通过该函数可以测试算法在存在多个极值时的全局寻优能力。
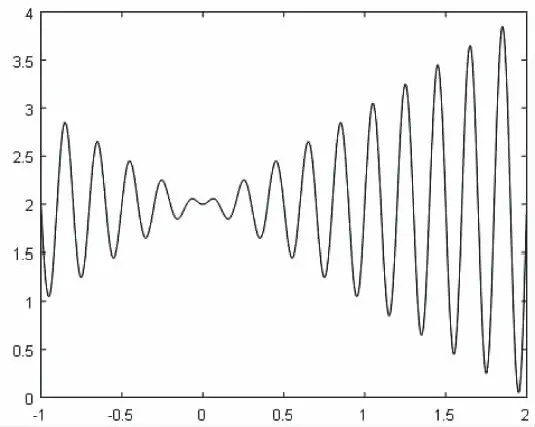
图5 函数f1图像
函数(7)图像如图6所示,在该函数定义域内存在多个局部最优点,其全局最大值为11.7525。当算法全局寻优能力较差时,算法易收敛于局部最大值10.8221。

图6 函数f2图像
x1,x2∈[-10,10]
(8)
式(8)函数是二元多峰函数,其函数图像如图7所示。在该函数中,每个峰顶都存在一个局部最大值,但该函数只有一个全局最大值1.0000。
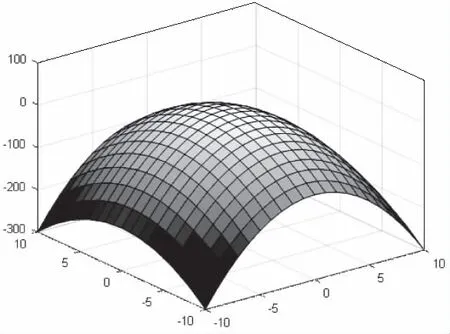
图7 函数f3图像
x1,x2∈[-10,10]
(9)
式(9)函数是二维复杂函数,其函数图像如图8所示。在函数定义域内,该函数具有无穷多个极值点,在(0,0)处取得全局最大值1.0000。由于该函数具有强烈震荡的性态,如果算法全局搜索能力较弱,则很容易陷入局部最优值。通过该函数可以测试算法跳出局部最优的能力。
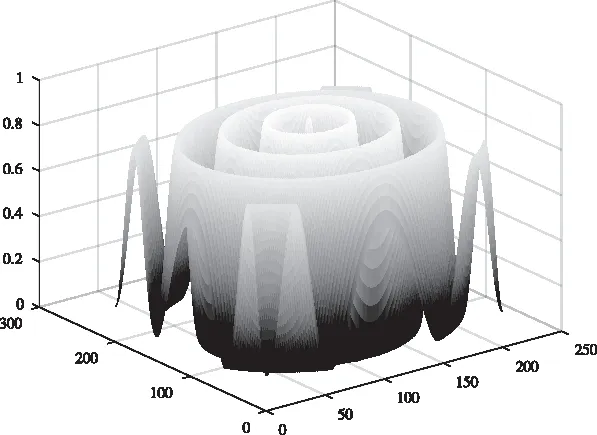
图8 函数f4图像
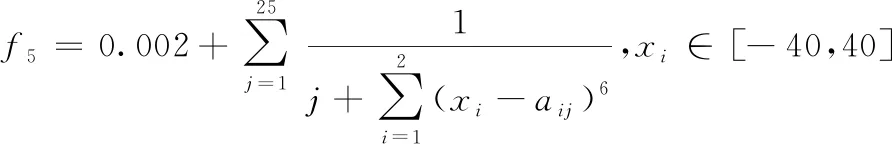
(10)
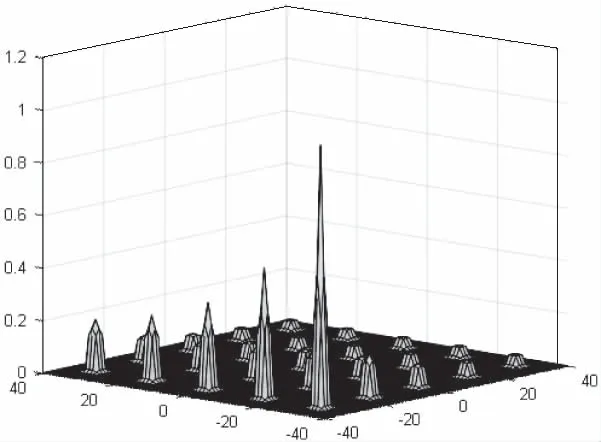
图9 函数f5图像
对上述5个函数进行500次寻优计算,其实验结果如表2所示。
由表2的实验结果可以看出,在5组测试函数中,AGA的平均收敛代数分别是本文算法的9.5倍、6.43倍、5.71倍、9.33倍、2.8倍;IAGA的平均收敛代数分别是本文算法的6.75倍、4.29倍、3.71倍、5.67倍、2.1倍。同时,在5组测试函数进行500次寻优计算时,AGA分别未收敛43次、47次、54次、51次、47次;IAGA分别未收敛37次、20次、17次、14次、21次,而本文算法不存在未收敛情况。由上述分析可知,本文算法无论在算法收敛性方面还是算法稳定上均优于其它两种算法。在平均收敛值方面,本文所提算法在测试函数1、2、3、5中,与AGA、IAGA相比,平均收敛值较大,与函数理论值的误差最小,更加接近函数理论上的最大值,且在函数1中,本文所提算法找到了函数理论上的最大值;在函数2中,本文所提算法的平均收敛值虽然比IGAG略低,但收敛次数与收敛代数比IGAG好。由平均收敛值可知,本文所提算法具有较好的全局寻优能力。
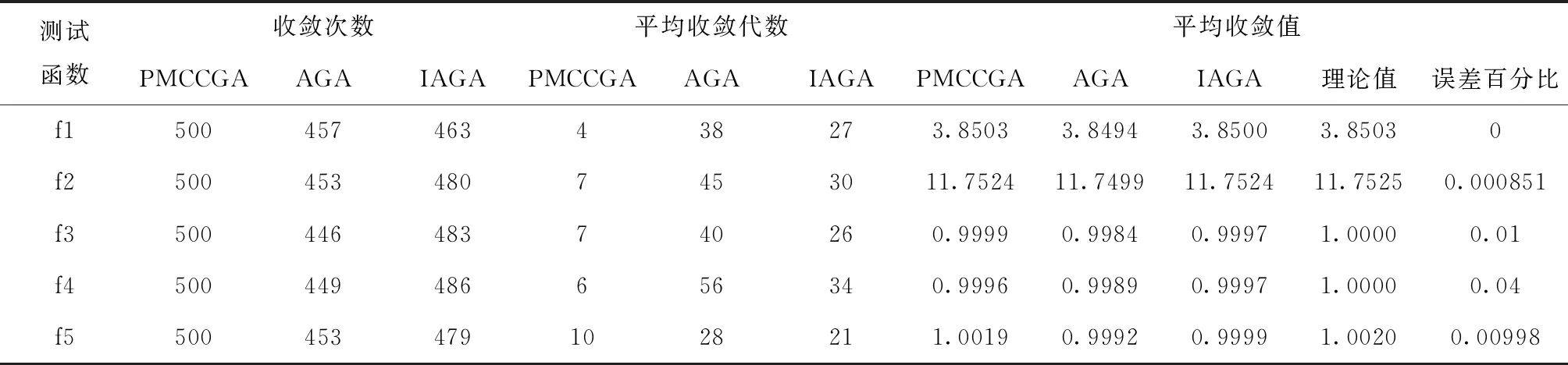
表2 3种算法在5个函数验证时的对比结果
实验三将本文算法与灰色关联分析法、粗糙集属性约简算法进行对比,通过ESSEEI数据集验证了本文算法在装备保障系统效能评估指标约简中的有效性,实验结果如图10、11所示。

图10 不同算法在SVM分类器中的分类准确率
图10为不同算法下约简的装备保障系统效能评估指标在SVM分类器上学习所得到的分类准确率。由图10可知,本文算法在ESSEEI数据集上具有更好的评估准确率,最高评估准确率为90.7%,而层次分析法与灰色关联分析法的最高评估准确率分别为87.8%和88.6%。同时本文算法能够选择更少的关键效能评估指标,所选效能评估指标个数为29个,粗糙集属性约简算法与灰色关联分析法所选效能评估指标个数分别为50个和43个。因此,本文算法能够在得到更高评估准确率的同时选择更少的效能评估指标个数。
图11为不同算法下SVM分类器ROC (Receiver Operating Characteristic)曲线图与AUC(Area Under roc Curve)值。ROC曲线将真正例率和假正例率结合,能够准确反映某种分类器真正例率和假正例率的关系。ROC曲线越靠近左上角,模型的准确性就越高。AUC值为ROC曲线所覆盖的区域面积,AUC值越大,其分类效果越好。由图11可知,使用本文算法约简后的装备保障系统效能评估指标作为SVM分类器的输入,其ROC曲线最靠近左上角,且本文算法的AUC值最大。

图11 不同算法下SVM分类器ROC曲线
5 结束语
装备保障系统效能评估过程中存在大量相互联系、相互冗余的效能评估指标,通过原有指标进行装备保障效能评估复杂度高且精度较低,因此,本文提出了基于改进遗传算法的装备保障系统效能评估指标约简算法。通过算法性能测试函数仿真结果表明,本文所提算法具有较好的收敛性能与全局寻优能力,将其用于装备保障系统效能评估指标约简,能够建立合理的装备保障效能评估指标体系,对装备保障系统进行准确评估。
