基于SLIC和马尔科夫随机场的H.264视频对象分割

王美杰，张起贵，李付江

(太原理工大学信息与计算机学院，山西 晋中 030600)

1 引言

视频序列中的运动对象分割是视频监控、视频编码及视频对象平面生成和检索等众多应用中的一个重要步骤[1]，根据使用的数据特征，现有的方法可以分为两类：像素域和压缩域。由于视频数据通常以压缩码流形式存储和传输，如果在像素域中进行运动对象分割，需要将压缩码流进行完全解码，然后利用解码后的数据进行目标分割，这样会显著增加运算复杂度，不适合应用在实时性要求较高的场合。随着近年来H.264压缩标准的广泛应用，人们越来越多的关注压缩域中视频对象分割，该方法的思路是直接从压缩码流中提取出运动信息，如DCT系数、运动矢量(MV)、宏块编码模式和量化参数等，因为避免了压缩码流的完全解码，因而有较少的计算时间，显著地减少了处理和存储的内存需求，可用于分割精度要求并不是很高的场合。

2005年Zeng等[2]利用从H.264压缩码流中提取的运动矢量进行运动对象分割，通过马尔科夫随机场分类过程从运动场中提取运动目标。然而，该算法只适用于对从固定摄像机拍摄的视频进行分割。2010年Chen[3]提出一种首先在MV场中进行粗分割，然后利用建立马尔科夫模型的方法提取出运动区域，最后利用颜色和边缘信息

进一步细化，但是引入的像素域信息增加了计算复杂度，降低了实时性。2015年Laumer[4]等提出一种利用从H.264/AVC视频比特流中提取的宏块类型来检测运动目标的算法，通过给编码宏块分配不同的权重来表示宏块属于前景或背景的概率。2016年Okade等[5]提出了一种新的粗分割技术，通过将帧间运动矢量分解成小波子带，并利用 LH、HL 和HH 子带小波系数的逻辑运算。2016年牛志国等[6]提出一种基于HEVC的运动分割方法，对从HEVC中提取的运动矢量进行时域和空域的标签分类，然后利用MRF模型进行运动一致性估计。2018年张鑫生[7]等提出了一种面向小运动目标的跟踪算法，利用从获取起始帧的掩膜、设置离群的MV以及对小目标的边缘预测三个方面来提高跟踪性能。

通过对上述文献的分析，发现这些方法鲁棒性不高，只对某些视频序列或某些帧分割效果较好。本文针对上述问题进行处理，提出一种基于改进的SLIC和马尔科夫随机场分割的方法，不仅鲁棒性强，而且分割效果较好。

2 算法描述

针对实际监控应用的特点，算法仅使用从H.264压缩视频流中提取的运动矢量。首先对运动矢量场进行预处理，然后进行改进的SLIC粗分割，随之构建基于马尔科夫模型的能量函数，同时引入可变权重的思想和通过运动场矢量直方图计算马尔科夫随机场似然函数的方法，最后使用图割法求解进而分割出运动对象。图1为本文算法的流程图。

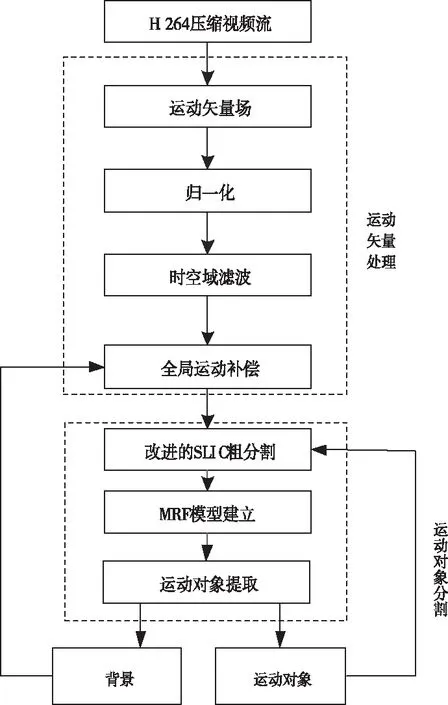
图1 算法流程图

从H.264压缩视频中获得的运动矢量，由于采用的是块匹配的运动估计技术，代表的是宏块的运动情况，并非运动估计的准确性，因此从码流中直接获取得运动矢量场有较多的噪声，并不能反映真实的运动情况，故在视频对象分割之前，需要进行运动矢量预处理，通常包括运动矢量归一化和时空域滤波。在H.264编码标准中，使用的帧内预测去除了相邻宏块间的空间冗余，提高了编码效率，但是由于帧内预测的宏块不含运动矢量，造成了对运动对象提取的困难，因此，需要利用未经帧内编码的宏块进行插值运算得到帧内编码块的运动矢量。本文采用文献[8]中介绍的极坐标矢量中值法。

在背景运动的视频序列中，需要进行运动估计以消除摄像机运动对分割产生的影响。本文使用8参数仿射模型[9]来表示全局运动，如式(1)

(1)

其中，(x，y)代表当前帧宏块的坐标，(x＇，y＇)代表八参数仿射变换矩阵变换后的坐标。最后对运动矢量场进行累加及全局运动补偿得到残差运动矢量场。

从图2可以看出，经过全局运动补偿后，背景运动的区域运动矢量得到减弱，而目标运动区域的运动矢量得到增强，因此通过全局运动补偿更有利于从背景运动场景中分割出运动目标。

图2 全局运动补偿

3 基于SLIC和MRF运动对象分割

3.1 SLIC算法描述

SLIC即简单线性迭代聚类算法是由Achanta[10]等人提出的，是一种思想简单、实现方便，采用K-means算法聚类生成的超像素的方法。文献[11]证明了SLIC相对于Normalized Cuts、graph-based approach、GraphCuts、Mean-shift以及Quick-Shift等超像素方法的优点。考虑到SLIC算法能生成紧凑、比较均匀的超像素，在运算复杂度、需要用户调节的参数少及物体轮廓保持等方面的优点，本文引入SLIC算法进行压缩域视频对象粗分割。

3.2 SLIC算法改进

SLIC算法首先将彩色图像从RGB颜色空间转换成Lab颜色空间，对应每个像素的(L，a，b)颜色值和位置坐标(x，y)组成一个五维向量Ci=[Li，ai，bi，xi，yi][12]。在实际应用中，只需要控制一个参数k，便可得到希望产生的超像素近似个数。SLIC采用式(2)到(4)来衡量第i和第j个像素的相似性。

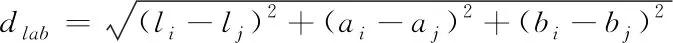
(2)

(3)

Ds=dlab+m/s*dxy

(4)

该算法首先生成K个种子点，然后在每个种子点的邻域内搜索最接近种子点的像素，并将它们与种子点分为一类，直到所有的像素点都分类完成。分别计算这K个超像素中像素的平均向量值，重新生成K个聚类中心，最后利用距离计算公式重复上述步骤，反复迭代进行更新聚类中心，通过计算新旧聚类中心的剩余误差直到满足指定的阈值时算法迭代停止。由图2 的观测结果表明，运动对象的运动矢量具有相似的方向和长度，其特征通常用幅度、散度和旋度来描述[13]，分别表示运动矢量的强度、伸缩度以及旋转度。由于本文采用SLIC算法对运动矢量场进行粗分割，所以需要对该算法进行修改。改进后的SLIC算法利用运动矢量的幅度M、散度D和旋度C以及宏块的空间位置(x，y)构造五维特征向量V=[M，D，C，x，y]。

(5)

其中(vx，vy)是运动矢量的两个分量。采用如下的公式计算宏块的运动矢量之间相似度。

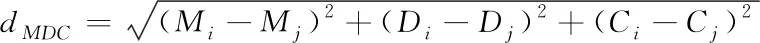
(6)

(7)

Ds=dMDC+m/s*dxy

(8)

其中(x，y)代表宏块的空间位置，dMDC代表宏块矢量间的差异性，Ds为结合宏块的空间距离和矢量相似性的归一化距离，m为紧密度系数。

3.3 基于直方图的MRF对象分割

由于SLIC的粗分割造成了图像的过度分割，如图4所示，因此需要利用宏块之间的邻域关系来提高分割效果。本文引入MRF模型来提高分割效果。MRF是一种基于统计的图像分割算法，通常在应用中与统计决策和估计理论相结合。MRF模型与贝叶斯估计框架下的最大后验概率(MAP)结合在一起称作MAP-MRF框架[14]。本文在MAP-MRF框架下，将运动目标分割问题转化为对运动宏块的标记问题，对于一幅待分割的图像，模型输出标记结果为ω=(ω1，…ωN)，ωi∈{0，1}，i=1，2….N，0表示背景，1表示前景。对于超像素块i的标号问题计算如式

图4 本文方法和文献[19]比较

(9)

其中P(MVi)为一常数，由运动矢量场事先给定。根据Hammersley-Clifford定理，MRF随机场与Gibbs 场等价，因此只要确定了Gibbs 随机场的能量函数如式(10)，也就确定了马尔科夫随机场[15]。

(10)

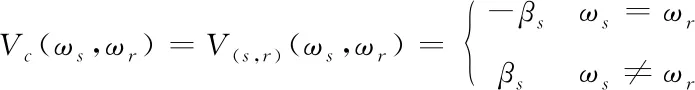
(11)

其中βs为模型参数，用来控制区域的同构性。

故式(9)等价于

P(ωi|MVi)∝P(MVi|ωi)·P(ωi)

∝exp[lnP(MVi|ωi)-U(ωi)]

(12)

其中E(ω)=∑-lnP(MVi|ωi)+∑U(ωi)。

由于后验分布也是一个Gibbs分布，因此求解P(ωi|MVi)最大问题转化成能量函数(12)最小化的问题。

对于文献[2]、[3]和[5]等传统的MRF分割方法中，势函数的选取一般都是固定的，这样没有充分考虑到节点之间的相互关系，使得分割效果不佳，很难同时保证边界的细节和良好的区域性。因此本文算法引入可变权重[16]的思想来提高实用性，使用自适应可变权重MRF分割模型，它的权重表示为指数形式：a(t)=c1·rt+c2，其中，c1，c2等于1/L，r是常量，t是当前迭代次数，于是得到自适应可变权重的MRF分割模型

E(ω)=∑-lnP(MVi|ωi)+α(t)∑U(ωi)

(13)

传统的MRF模型使用聚类算法把前景和背景分别分为几类，需要聚类过程的先验知识来创建前景混合高斯模型和背景混合高斯模型来估计似然函数P(MVi|ωi)，即

(14)

其中mωiX和mωiY分别是标记为ωi块的MV的水平和垂直分量的均值，σωiX和σωiY为相对应的标准差。

对于这种统计建模方法而言，虽然在处理性能上效果比较好，但同时也引入了较高的计算复杂度，仅适用于少数动态背景序列和静止背景序列。在本文的方法中，式(13)的P(MVi|ωi=0)和P(MVi|ωi=1) 是通过计算背景和运动区域矢量直方图得到。对于给定标号ωi=0或1，运动矢量直方图中共有m个bin，K是bin中对应的运动矢量总个数，对于给定的MVi，k是在bin中对应的样本数，则条件概率为(15)：

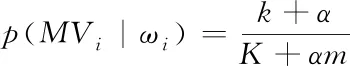
(15)

其中α>0是平滑因子。实验中α取0.9。

图3为Stefan视频序列第25帧运动矢量的直方图。

图3 Stefan视频帧运动矢量直方图

在贝叶斯框架下，常用的求解能量函数的方法有：模拟退火(SA算法)、迭代条件模式(Iterated Conditional Mode, ICM)和图割法(GC)[17]。由于前两种方法容易陷入局部最优和有收敛速度慢的缺点。本文算法采用GC法求解式(13)，克服了前两者的不足。

4 实验结果与分析

实验采用典型的stefan视频序列(CIF，352×288)、foreman视频序列(CIF，352×288)和garden视频序列(CIF，352×240)：编码使用的编码器为JM18.6，编码格式为IPPPP…，量化步长QP为28，搜索范围为(-32，32)。然后与文献[19]方法进行了对比。

选取的三个视频序列均属于背景运动的场景，本文算法同样适用于静止背景的场景。其中第一、四、七行为文献[19]的分割结果，第二、五、八行为改进的SLIC算法的分割结果，第三、六、九行为本文算法的最终分割结果。Stefan序列为运动员运动剧烈且背景比较复杂的视频序列，由于运动员产生的运动矢量较大，因此本文算法对该序列有更强的鲁棒性。对于foreman序列，文献[19]出现过分割而且人物的边缘粗糙。在garden序列中，摄像机从左到右移动拍摄，本文算法可以将树干更准确的分割出来。从图4 可以看出，文献[19]方法和本文方法都能分割出视频序列中运动对象，但是文献[19]在视频序列后续帧分割效果较差，鲁棒性低，本文的方法相对更多的消除了背景区域，鲁棒性较好。虽然在目标物体的边界附近出现了一些错误的检测，但是对物体内部的分割效果很好，提取的轮廓相对更小，运动对象边缘检测更精确。由于本文方法是基于宏块的分割，仍然存在边缘模糊性的问题。

为了客观评价算法分割结果，本文与文献[19]从精确率(P)、召回率(R)和F-Measure值三方面进行对比，如表1所示。

表1 本文方法与文献[19]在P、R、F比较

(16)

其中TP为正确检测到的样本像素点，FP为错误检测到的样本像素点，FN为错误检测的负样本像素点[18]。

从表1可以看出，本文方法相比文献[19]具有较高的P和F-Measure，R有时低于文献[19]，是由于本文算法将前一帧运动目标的运动区域映射到当前帧进行分割，因此从对象中排除落入标记为背景的边界块的像素，从而导致更高的FN。

本文方法分割的计算时间如表2所表示。

表2 本文方法与文献[19]计算时间比较

本文提出的方法计算时间包括运动矢量归一化和时空域滤波及基于SLIC和MRF分割，由表2可以看出，与文献[19]方法相比，运算速度平均提高了1.85倍。为了进一步比较运算复杂度，将本文所提出的压缩域视频对象分割方法与Papazaglou等[20]提出的一种先进的像素域视频分割方法进行了对比分析并给出了该方法的分割结果。

图5 文献[20]和本文方法分割比较

从实验结果可以看出，文献[20]的方法与本文的方法相比取得了较好的分割结果，然而，本文方法的一个主要优点是计算成本减少了几个数量级，如表3所示。

表3 本文方法与文献[20]分割时间比较

本文压缩域算法比文献[20]像素域算法的复杂度低，主要是因为压缩域中复杂的解码步骤被简单的解码器的语法解析所取代。其次，由于压缩域不必处理所有像素，算法本身的复杂度较低。

5 结论

本文提出一种基于改进的SLIC和马尔科夫模型的H.264视频对象分割算法，不需要对压缩码流进行完全解码，因此，该方法具有较低的处理时间。预处理阶段包括运动矢量场归一化和时空域滤波两部分。为了消除摄像机移动对分割产生的影响，进行了全局运动估计和全局运动补偿，之后建立MRF模型进行运动目标分割。①引入了SLIC的方法，不仅提高了视频中每一帧分割的鲁棒性和准确性，而且解决了MRF模型参数估计及推断时间复杂度较高的问题。②引入可变权重的思想，增强了分割效果，扩大了算法的适用范围。③利用直方图进行似然函数的计算，避免了聚类过程陷入局部最优解的问题并且显著地降低了计算成本。④H.264编码标准在当前市场的摄像机中广泛使用，由于本文算法是基于视频码流中提取的运动矢量分析，不依赖于H.264特定的标准，因此该方法可以很方便地扩展到其它的编码标准。

实验结果表明，该方法可以在复杂背景下分割出运动目标，鲁棒性和准确性较高，计算复杂度较低。由于算法在运动宏块基础之上处理，标记场是以宏块为单位的，处在目标边缘处的宏块中的像素点并不是全部处于前景区域或背景区域，因此会产生误差，对于提取的运动对象存在过分割或者轮廓偏大的现象有待进一步改进。