基于切换系统的城轨列车ATO控制策略研究

2021-11-17谌飞雨邱存勇

计算机仿真 2021年7期

谌飞雨，邱存勇

(西南石油大学电气信息学院，四川成都 610500)

1 引言

随着现代社会节奏的不断加快，城市轨道列车的人工驾驶在许多城市已经被ATO控制系统[1]替代，城市轨道列车地运营变得更加高效和安全。有轨的列车运行过程实质就是不同工况的频繁转换，其运行环境多变，动力学特性体现为非线性和时变性[2]。在 ATO 系统的发展过程中，研究者们尝试将不同的控制算法引入到 ATO 系统中，主要包括模糊PID 算法[3]、预测型灰色控制算法[4]、神经网络控制算法、遗传算法[5]等。其中应用最成熟使用最早的是模糊PID控制。PID 控制方法是基于分析列车动力学的简化模型如系统的传递函数，此方法将列车运行过程建立成一类单输入单输出模型，对列车的控制手法单一化。因此当出现外界干扰时，列车需要减速停车，无法满足正常的运行。另一方面在靠站过程中需要人为操控，无法满足全过程自动控制需求。神经网络控制算法基于人工神经网络建立复杂的数学模型，控制精度及智能程度高，但是建立过程所需数据及工作量庞大，造价较高。遗传算法为一种并行随机搜索最优化的算法，对问题的种类有很强的鲁棒性，但是因为其计算时间过长处理速度过慢的缺点，用于实际工业过程仍有很大局限性。灰色预测控制根据已知的信息对工业对象处理进行优化，并根据未来输出结果预测值随时调整，但该过程会产生冗杂的储存数据，占用大量空间。

列车运行过程中的速度变化和工况的改变，具有明显的切换特性[6]，因此将切换系统理论应用到城轨列车的ATO系统中是必要且可行的。切换系统理论是基于状态空间模型的。系统的状态空间模型是一种具有多输入多输出特性的数学模型[7]。基于状态空间模型的控制方法中，可以通过控制其某一状态量对整个系统进行控制，在有外界扰动的时候以及系统状态变量频繁改变的时候，状态空间模型的控制方式更加灵活。

本文将列车的运行控制过程看作一个切换系统，将不同的运行工况分别建立成不同的子空间，当列车运行环境变化导致其运行速度改变时，控制系统自动切换到对应工况，保持列车平稳有效地运行。具体地，首先对城市轨道列车的运行过程进行了受力分析，并列出了其运行过程各工况的动力学模型。然后用数学软件对动力学模型求解得出其运行特性图，用系统辨识方法得到各个子系统的状态空间方程[8，9]。之后对列车的运行过程在预设路线的条件下进行仿真，分析其运行特性图，在保证安全和稳定运行的条件下，设计其各工况的切换规则，得出运行过程的切换点，最后通过仿真验证该切换策略控制下的列车是否能正确地在终点停靠及列车运行在外界扰动下的有限时间稳定性[10]。

2 运动学建模

2.1 受力分析

列车运行过程的外界影响较多，比如气候，路况等，将其受力类型分为牵引力，阻力和制动力。为简化计算，将列车模型车厢链接视为刚性链接。

牵引力[11]是列车运行的主要动力来源，由列车发动机的牵引特性决定。通常列车启动时其牵引力如式(1)所示

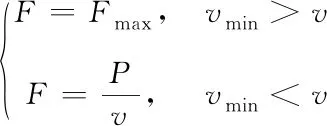
(1)

式(1)中Fmax为A型地铁的最大牵引力，单位N。P为列车的实时牵引功率，单位W。v为列车实时速度，vmin为列车规定最小速度，单位都为单位m/s。

列车运行过程中有两个主要的阻力：基本阻力和附加阻力。

列车运行单位基本阻力通常使用工业实践所得出的如式(2)所示经验公式来表示：

ω0=a1+a2v+a3v2

(2)

上式中a1，a2，a3为三个经验常数由列车自身特性决定，v为列车实时速度，单位m/s。ω0为列车单位基本阻力，单位N(kN)。本文所研究的列车型号为A型地铁，其单位基本阻力公式为

ω0=1.599+0.0143v+0.000243v2

(3)

附加阻力因轨道的路面情况变化而产生，分为坡道阻力和曲线附加阻力。车辆上行坡道单位基本阻力

ωi=mgsinθ≈mgtanθ=i

(4)

θ为坡道角度，i为坡道坡度，单位‰。

列车在弯曲轨道运行时，车轮与弯道间挤压产生摩擦力，通常采用由实际实验所得经验公式表示弯道单位基本阻力

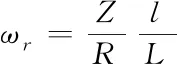
(5)

式(4)中Z为经验常数，本文取600。L为该路段总长，l为弯道长度，R为弯道半径，单位都是m。

列车制动分为空气制动和动力制动。

动力制动力大小由所需要的制动加速度及列车当前运行速度决定。

(b=ma(1+γ)-mgω10-3

(6)

式(5)中b为列车单位基本制动力，m为列车质量，a为列车当前所需的制动加速度。γ为列车回转质量系数，即列车回转质量与列车总质量之比。ω为当前列车单位基本阻力。

空气制动即停止牵引利用轨道阻力进行制动，为惰行工况。

2.2 运动学方程

根据列车运行状况可将列车运行过程分为三种工况：牵引，惰行和制动。这三种工况满足一定的规则下相互转换。

表1中√ 代表两种工况之间可直接转换，×代表两种工况相互转换时需其他工况过渡。在不同工况下列车的所受合力也有所不同。

表1 工况转换规则

牵引启动

c=f-ω0-ωi-ωr

(7)

匀速牵引

c=0，f=ω0

(8)

惰行

c=-ω0-ωi-ωr

(9)

动力制动

c=ωi-b-ω0

(10)

列车运动过程合力与加速度关系为

c=ma(1+γ)

(11)

上述式子中c为列车所受单位合力，ω0为单位基本阻力，ωi为坡道附加单位阻力，ωr为弯道附加单位阻力，b为单位制动力，单位都为N(kN)。

根据牛顿运动定律，可得出列车运行过程中加速度及位移与列车速度之间的关系式。

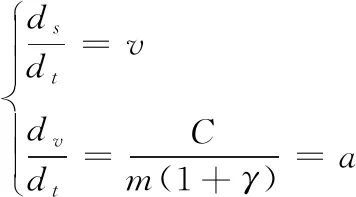
(12)

式(12)中a为列车当前加速度，单位m/s2，C为列车所受合力，单位N。

2.3 列车和轨道参数

本文研究的A型地铁，其基本参数如表2[12]。

表2 列车基本运行参数

A型地铁标准持续运行速度80km/h，启动过程规定最低速度为40km/h。

列车运行轨道路线是固定的，讨论列车实际运动过程就需要设计相应的线路

本文通过简单计算A型地铁的运动情况，设计一条简单实验线路，并将其简化，具体参数如表3所示。

表3 简化线路参数

2.4 状态空间模型

切换控制系统与传统的模糊PID控制不同，是将列车的运行系统根据不同的工况建立成不同的子系统，分别对每个子系统建立相应的状态子空间模型。

建立如下的状态子空间模型

xt=h(xt，ut)+εt

yt=g(xt，ut)+γt

(13)

式中下标t表示列车运行时间，yt是输出向量，表示列车速度，位移的一个2阶矩阵。ut为表示列车牵引力的一个标量，与列车速度及工况的牵引功率有关。xt为列车的状态向量，为一个与速度位移有关的函数。h和g为非线性向量函数，εt和γt为扰动项(本文主要由坡道参数变化影响)。

如果直接求解式(13)计算量大，这里分析列车运行稳定点工作情况将上式近似写为如下的状态空间方程

(14)

针对式(14)求出其参数矩阵A，B，C，D的值即可解出该子系统的状态空间方程，具体过程如下。

由列车受力及运动过程分析，列车的动力学特性状态空间模型可表示为

(15)

对左右两边进行求导，建立近似的切换系统模型

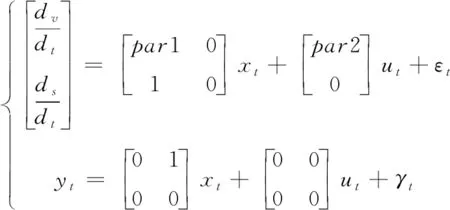
(16)

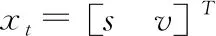
3 运动数值仿真及切换系统模型地建立

3.1 运动过程仿真

要求得对应的参数矩阵及各个子状态空间方程的初值，需利用MATLAB的系统辨识工具箱对模型的状态空间方程进行系统辨识。而要进行系统辨识，还需要列车的运行特性曲线图。

由于列车运动过程数学模型为与运行速度和距离相关的微分方程式，为了直观地表示列车的运动特性以方便设计切换控制策略。利用MATLAB对列车的运动方程进行求解仿真[13]。

设定仿真时间及初始速度位移并代入路面参数，即可求得某一时间段内列车运行特性图[14]。根据列车的运行特性图可以确定其运动过程中的切换点，设计其控制规则。

列车启动时，电机以最大牵引力启动，设置初始速度及位移都为0，进行MATLAB仿真，得出如图1所示的运行特性图。

图1 初始启动工况列车运行图

根据运行特性图经计算可得，列车运行61m之后速度达到40km/h。以该速度为初值，仿真列车在直线路段恒定功率牵引工况的运行特性，如图2所示，根据运行特性图找点计算，列车运行292m后速度达到80km/h。

图2 直线恒定功率牵引工况运行图

将下坡路段路面参数代入仿真，以80km/h的速度作为初值，首先仿真列车在直线路段匀速牵引的工况进入下坡路段后的运行特性图，如图3所示。

图3 下坡段稳态牵引工况运行图

由运行特性图经计算可得，列车运行2730m后，速度达到90km/h。以此为初速度，仿真在下坡路段的惰性工况，得出如图4所示的运行特性图，可得出列车运行8820m后，列车速度达到100km/h。

图4 下坡路段惰行工况运行特性图

最后以100km/h为初值，仿真下坡段动力制动运行特性图，如图5所示，运行175m后速度降至90km/h。

图5 下坡段动力制动运行图

最后对直线路段的空气制动工况(即惰行)进行仿真初值设为80km/h，如图6所示，列车运行9910m左右速度降至40km/h。

图6 空气制动工况运行特性图

3.2 切换模型地建立

切换系统包括该系统的切换控制策略及其状态空间模型。

这里切换策略根据其运行特性图选取合适的切换点设计控制策略，切换点的选择遵循表2所给出的列车速度限制规则，所设计的控制策略要满足列车在末尾路段能够准确地停车，以及下坡路段不会失速的准则，同时考虑了乘客舒适度问题(即整个过程列车加速度除了启动过程以及停车过程均小于等于1m/s2)。

初始启动过程中，初速度为0，加速度为0，为了让列车尽快达到规定的最低速度，以最大牵引力工况加速运行。当速度达到40km/h后，如图1所示，加速度过快，考虑节能性，为使列车更平缓地加速到标准持续运行速度，切换为恒功率牵引工况加速运行。如图2所示速度达到80km/h后，为了尽可能的节能运行及保证乘客舒适，切换至稳态牵引工况匀速运行。

保持匀速运行进入下坡路段后，运行特性如图3所示，因受到向下的附加阻力，变为加速运行。当速度达到90km/h后，参考表1速度过快由牵引工况切换为制动工况前，需由惰行工况过度，因此切换为惰行工况运行。考虑节能性，保持惰行工况达到100km/h的最大运行速度再切换为制动工况进行制动。如图5所示，当速度降至90km/h后，考虑节能并最大化利用下坡附加的动力，再次切换为惰行工况，并保持进入最后的直线路段。

进入最后路段后，由于是平缓直线路段，列车只受轨道附加的基本阻力惰行工况变为图6所示的减速运行状况，速度降至80km/h后，为保证准确停车及乘客的舒适性，切换为稳态牵引的匀速运行工况，直到距离停车点10km处，切换为惰行工况，进行空气制动，使速度降至40km/h，然后进行最大制动力制动，保证列车在终点站停车。

总结运行策略如下：

切换关系图如图7所示。

图7 各工况关系图

根据运行特性图并结合建立的切换系统模型公式，使用灰箱辨识，求出其状态空间方程参数矩阵，如下坡路段的牵引工况的子系统如下。

下坡牵引

(17)

将切换控制策略里的切换点，代入各子系统切换系统模型进行仿真，可以得出切换控制下每个路段的速度变化特性图。得到列车切换系统模型及切换控制策略后，需对所设计的控制策略的可行性进行验证。

4 切换模型地验证

4.1 停车问题分析

列车准确靠站停车是ATO控制最主要的研究对象，这里对最后一个路段的制动切换过程进行仿真，观察列车是否能够在终点站稳定停车。

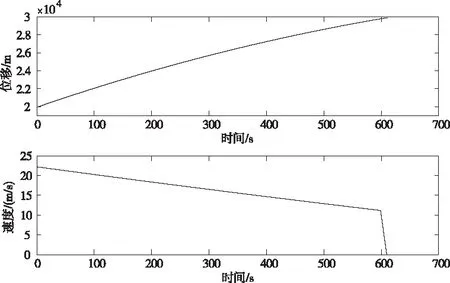
图8 靠站路段切换过程运行图

由仿真图可得，列车在所设计的切换规则控制下能够在预定的路线内稳定停止运行，而达到靠站目的。

4.2 有限时间稳定性分析

对于以往的列车ATO控制，在少量扰动的情况下，模糊PID控制可以在模糊规则内调控系统使其保持稳定运行，而出现其规则外干扰使得列车运行速度达到危险区间时，其给出的反应是直接切断电源，使列车停止运行。但对于切换系统，直接根据速度及路程进行调控，速度及路程达到一定值时，会根据速度自行切换工况，使速度维持在安全运行范围内。但是在切换过程中，可能会出现过度工况的转换，因此在过度工况的工作区间内速度不超过规定最大值，即可证明该系统的有限时间稳定性[15]。

要讨论本文所建的列车模型的稳定性的关键在于下坡路段切换时间区间内运行速度是否会超过100km/h。

下坡路段外界干扰考虑暴雨天气情况下，空气湿度和轨道湿度增加，此情况下列车受到的本阻力会减小，单位基本阻力为：

ω0=1.05+0.002v+0.000126v2

(18)

将该阻力系数代入下坡路段公式进行重新计算。

对于列车下坡过程进行分析，根据前面所设计的切换控制策略，列车速度达到90km/h后会进入惰行工况，而根据列车牵引电机特性，在不损坏电机寿命及非紧急制动状况下从正转牵引工况切换至逆转制动工况时间需要120s时间。