基于增强学习的车辆转弯制动横向轨迹控制
2021-11-17罗锦才刘暾东
罗锦才,刘暾东
(厦门大学航空航天学院,福建 厦门 361102)
1 引言
近几十年,汽车行业得到了大规模的发展,私家车保有量也大幅度提升,道路交通压力逐渐增大,交通事故频发,引起了人们对于私家车安全性能的高度重视。根据交通事故发生前后的时间不同,将车辆的制动控制分为多种情况,其中车辆转弯是一个十分常见的问题。根据相关数据统计,发生的交通事故中有79%是由于车辆转弯制动问题所导致的,此类交通事故往往都会造成非常严重的后果,重则会影响驾驶员的生命安全[1-2]。
根据上述方法存在的问题,本文提出基于增强学习的车辆转弯制动横向轨迹控制方法,并对其进行仿真测试,验证此控制方法的可行性与科学性。
2 车辆转弯制动横向轨迹控制方法设计
2.1 构建车辆动力模型
在此次研究中,将通过构建车辆动力学模型的形式为车辆转弯制动横向轨迹控制方法提供数据基础。根据车辆动力学原理与特性,采用ADAMS软件[5-6]作为模型构建平台。在此软件中,根据动力学原理将车辆划分为多个刚体,并对刚体的质量与各个方向的动力惯性进行定义与赋值。在车辆模型的构建与计算过程中,采用分析法与试验法相结合的形式得到车辆运动微分方程组,具体计算过程如下。
为了更加客观的体现轮胎的力学特性与参数,构建对应的SAE坐标系[7],此坐标系为右手坐标系,将垂直于车轮旋转轴线的轮胎中分面设定为车轮平面。设定坐标系的原点O为车轮与地平线的交线与车轮旋转轴线的交点。车轮平面与地平面的交线为X轴,设定方向向前为正向。Z轴与地平线垂直,正方向向上。Y轴为地平面,车轮前进方向向左为正。在车辆行进的过程中,车轮分别受到X轴、Y轴与Z轴的三个方向的力与绕这3个轴力矩的作用,根据原有研究结果,将此部分力称为轮胎的六分力,分别为:纵向力Fx、侧向力Fy、法向力Fz、侧倾力矩Rx、转动力矩Ry以及回正力矩Rz。根据上述设定,使用三角函数得到轮胎六分力的联合作用情况,通过拟合计算的形式,获取水平方向漂移数据及其侧向力,具体计算过程如下:
Fy0(β)=Sysin(Cyarctan(Byβ-Uy(Syβ-arctan(Syβ))))
(1)
式中,Fy0(β)表示纯滑移条件下计算得到的横向力的值;β表示车轮偏转角;S表示上述两公式的峰值因子,即动力曲线的最大值;B表示刚度因子,且B=BCS/(CS);x表示轮胎的侧向力、纵向力与回正力矩;y表示车辆轮胎的偏转角;C表示曲线形状因子,决定着曲线的形态特征。在上述参数中,除形状因子C外,全部参数与轮胎的垂直负荷具有函数关系。将车辆数据带入此公式中,进行拟合可得到相应的车轮轮胎模型在纯滑移条件下的变动系数。根据变动系数,构建车辆动力模型,具体公式如下
φ=(1-P)(X+Wl)Fy0(β)+(P/B)arctan(B(X+Wj))
(2)
在上式中,P表示曲线曲率因子,即动力学曲线最大值附近的形状;Wl表示车辆垂直方向漂移;Wj表示车辆水平方向漂移。在此次研究中,将此部分数据作为控制方法的数据来源。
2.2 构建滑移率目标函数
车辆转弯制动是一种更为复杂的工况,它不同于直线制动工况,转弯制动时的载荷转移和大侧向滑动对制动稳定性动力学控制提出了更高的要求,而车辆蔽障过程伴随制动,由于实际车辆转向制动作业工况下不稳态的横摆角速度和最佳滑移率不确定性导致车辆整车侧倾,车辆极易失去控制,因此对车辆转弯制动横向轨迹进行控制。根据上述部分中设定的车辆动力模型,将其简化为线性的二自由度系统[8-9],将车辆的滑移率作为优化的参数,其中滑移率与附着系数作为目标函数的组成部分,考虑到制动过程中的减速情况与车辆的稳定性,将此次控制参数的优化目标函数设定如下
mine=(χ-χdes)2+(v-vmax)2φ
(3)
在上式中,x表示转弯制动过程中的车辆轮胎横摆动角;χdes表示前轮转角和车速稳定的情况下稳态的横摆角速度;v表示车辆的减速度;vmax为地面所能提供的最大减速度。当上述公式取值为最小值时,所得到的滑移率为控制过程中的最佳目标滑移率。通过对式(3)的推导可知
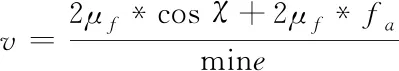
(4)
式中,μ表示轮胎的附着系数[10]。
金融开放度与经济增长之间是否存在非线性关系是本文的研究假设1同时也是后文的研究基础。对此我们依据模型(1),对各国金融开放程度与其经济增长之间的相关关系进行检验。估计结果可见表4。
对上述公式进行整合可得到滑移率与附着系数之间的转换关系
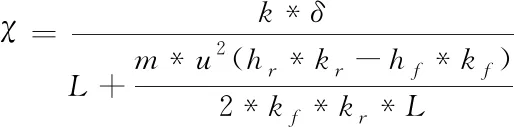
(5)
式中,L表示车辆滑移长度,hr、hf表示车辆轮胎的转动系数,kr、kf表示车辆的滑移计算常数。通过此公式可得到最优横摆角速度χdes,具体公式如下所示
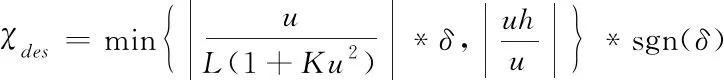
(6)
稳定转向下的横摆角速度会低于其物理极限值,因此,χdes可简化为
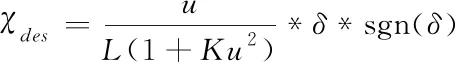
(7)
将此公式代入到式(3)中,即可得到需要优化的车辆控制参数。
2.3 实现车辆轨迹控制
由上文可知,车辆横摆角速度目标函数的取值为最优解时为车辆的理想状态。鉴于车辆制动过程中的稳定性,使用增强学习算法对其运动轨迹进行控制。此次设计的控制方法需要构建相应的控制器作为方法的实施平台。将控制策略通过参数的形式体现如下
πα(s,a)=P[a|s,α]
(8)
式中,α表示策略权重,π表示控制策略内容。πα(s,a)表示使用函数α后进行函数拟合所得策略函数[11-12]。使用增强学习技术对上述问题进行求解,可获取车辆动作为α时的概率。在此计算环节中需要设定对应的数据量对多种控制策略进行衡量,此数据量为控制目标策略函数。无论何种目标策略函数K(α)对于何种πα(s,a),都符合下述约束要求。
∇αK(α)=Eπ[∇αlgπα(s,a)Qπ(s,a)]
(9)
式中,∇αK(α)表示目标控制策略函数K(α)的梯度。同时,梯度∇αlgπα(s,a)可以通过高斯策略获取。Qπ(s,a)表示计算过程中的动作值函数,使用策略梯度算法可得到计算结果。由于此部分计算过程具有一定的连续性,因而采用连续型增强学习算法得到最佳控制策略。设定在测量集合Z中具有控制状态z,此策略参数为γ,使用γ与z求取不同动作c下的概率函数,具体公式如下
fα(z)=η(z)Tγ
(10)
式中,η(z)表示特征向量,fα(z)表示控制策略的特征函数。使用高斯函数对其进行求解,则有
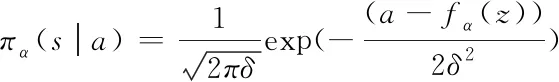
(11)
通过此公式,可得到最终的控制策略对数梯度,具体如下
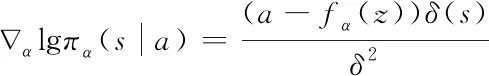
(12)
使用此公式可对已获得的控制策略展开处理,并得到适用于车辆转弯制动横向轨迹控制的最佳控制策略。将控制策略集合中的全部策略代入上述公式中,对比对数梯度计算结果,得到最优解,并使用此策略完成车辆横向轨迹控制过程。至此,基于增强学习的车辆转弯制动横向轨迹控制方法设计完成。
3 仿真分析
3.1 仿真条件设定
为了证实本文提出的基于增强学习的车辆转弯制动横向轨迹控制方法在日常的使用中具有相应的优越性与可靠性。在此次实验中,将采用其与目前使用方法对比的方式,深入研究此方法的使用效果。为了体现不同初始车速对于车辆控制效果影响,在此次实验中使用仿真的形式,并将仿真条件设定如下:前轮转速由0到0.5s逐渐上升到0.05rad;制动从1s开始,即转弯开始后0.5s开始制动;仿真道路附着系数为0.70;控制目标车辆滑移率为0.20。控制误差与误差变化量的量化因子以及输出变化量比例为15:2。根据上述设定的仿真参数与车辆情况,使用文中设计方法与文献[3]提出的转向制动工况下平衡重叉车横向稳定性控制方法和文献[4]提出的基于可拓优度评价的智能汽车横向轨迹跟踪控制方法对车辆转弯制动横向轨迹进行控制,对比控制效果。
3.2 实验方案设计
在此次实验中,将实验指标设定为车辆滑行时间、车辆位移长度以及车辆整体滑移率。通过上述实验指标对比文中设计方法与文献[3]方法、文献[4]方法的应用效果。为使实验结果更加逼真,将车辆的初始车速设定为15m/s以及30m/s,制动过程中车辆速度变化均匀,控制力矩稳定,车轮载荷一致。仿真共进行5次,通过数据与图像的形式,完成文中设计方法与文献方法的对比过程。
3.3 控制后车辆滑行时间对比结果
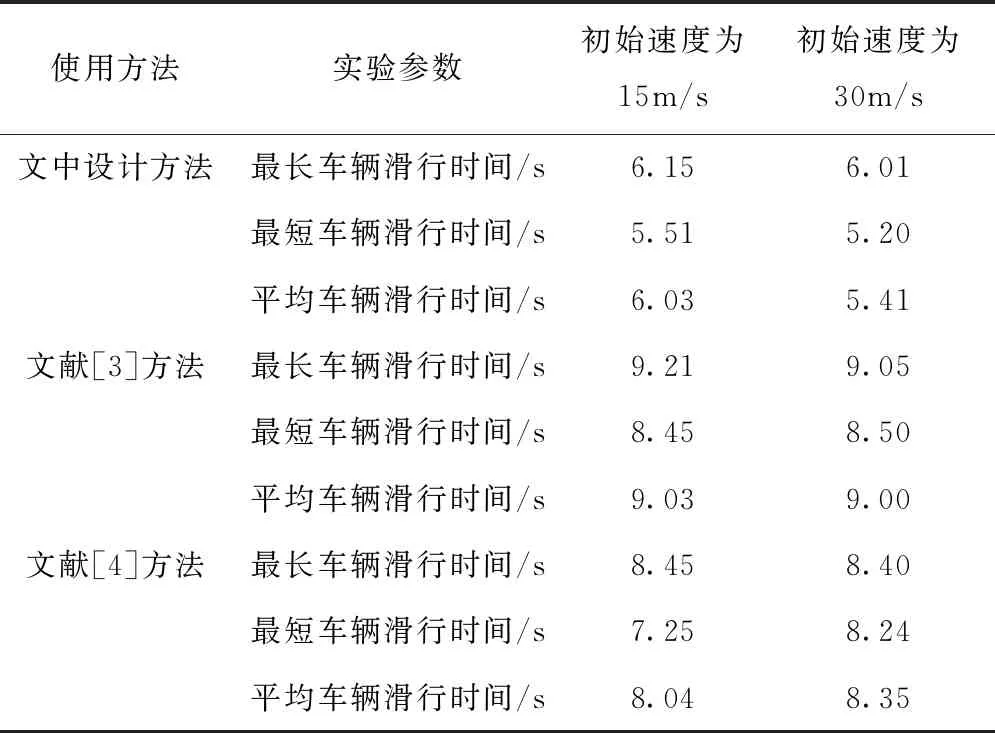
表1 控制后车辆滑行时间对比结果
通过以上实验结果可以看出,文中设计方法的使用效果明显优于文献[3]方法和文献[4]方法。通过数据对比可以看出,文中设计方法在两种初始速度下均可较好的控制车辆滑行时间。同时,通过实验数据也可以看出文中设计方法的车辆滑行时间区间较短,由此可知此方法在使用的过程中可在较短的时间内完成。相较于文中设计方法,文献[3]方法和文献[4]方法虽然对于车辆具有一定的控制能力,但其控制响应时间较长,在实际使用中易造成交通事故。由此可判定,在此指标对比中,文中设计方法的使用效果更佳。
3.4 控制后车辆滑行长度对比结果
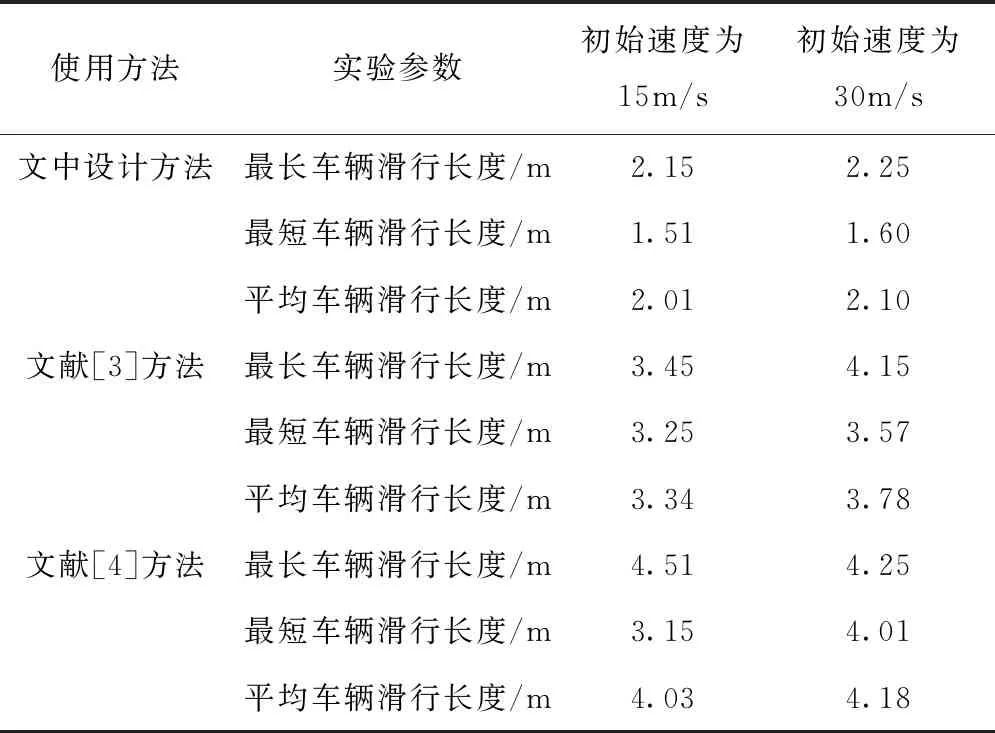
表2 控制后车辆滑行长度对比结果
根据以上表格中数据可以看出,文中设计方法在此实验环节中所得实验结果优于文献[3]方法和文献[4]方法的实验结果。根据多次实验与测算,在不同车辆初始速度下,文中设计方法的使用效果一直维持在较为平稳的状态下。但通过数据可以看出,文献[3]方法和文献[4]方法使用效果并未达到文中设计方法的高度,两种方法在使用后会造成车辆滑行路程较长,加大了车辆交通事故的发生几率,导致驾驶员的安全出现问题,不利于交通安全管理。因此,在此部分实验中可知,文中设计方法的使用效果优于文献[3]方法和文献[4]方法。
3.5 车辆整体滑移率对比结果
通过以上实验结果可以看出,在两种不同的初始速度下,文中设计方法控制下的车辆整体滑移率较低,同时不同的初始速度对于车辆整体滑移率的影响较低,文中设计方法的使用效果较为稳定。相较于文中设计方法,文献[3]方法和文献[4]方法对于车辆的整体滑移率控制效果较差,车辆的初始速度很容易对控制方法的使用效果造成影响。在不同的车辆初始速度下,文献[3]方法和文献[4]方法的控制差异较大,直接影响了车辆的横向轨迹控制效果。由此可知,文献[3]方法和文献[4]方法不如文中设计方法的使用效果稳定。
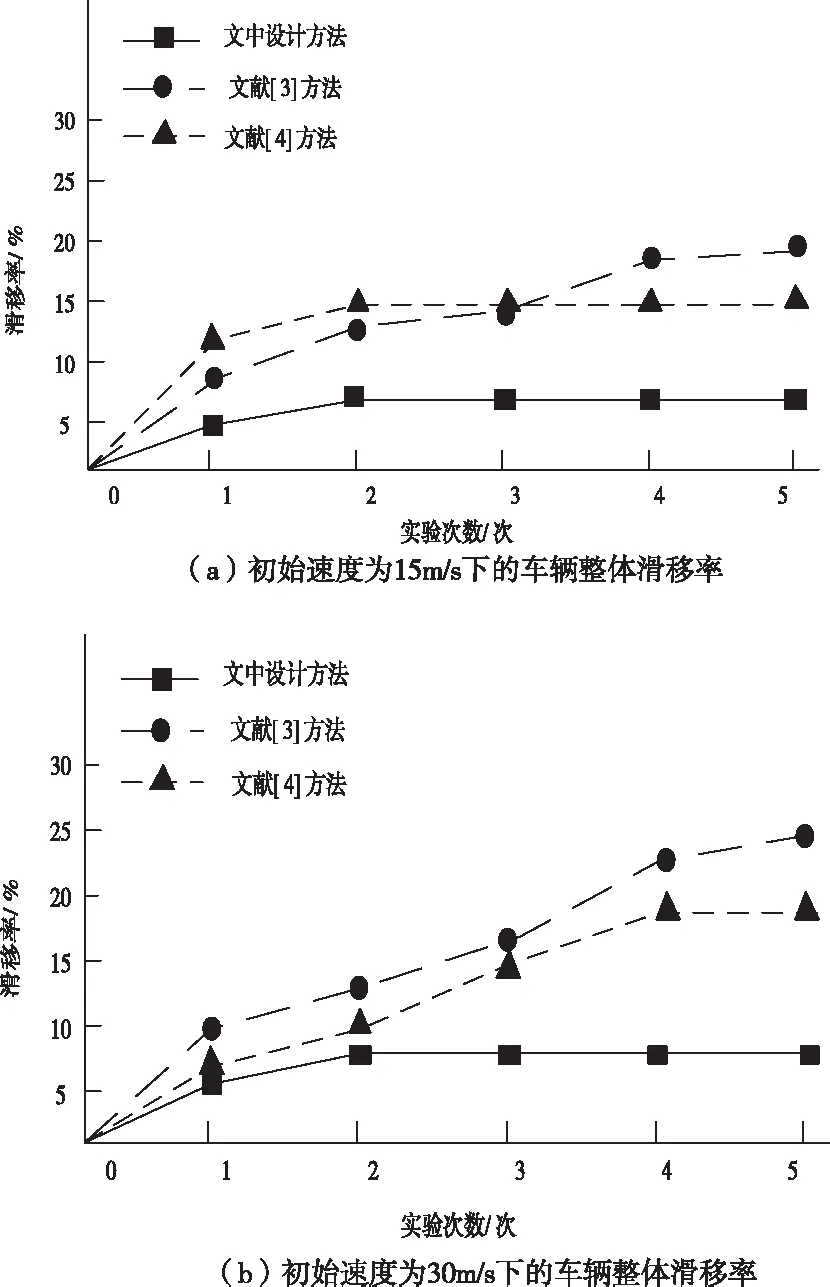
图1 不同情况下的车辆整体滑移率对比结果
将以上实验结果进行综合分析可以看出,文中设计方法的使用效果明显优于目前使用中的控制方法。在日后的研究中,可使用此方法作为车辆的最佳控制方法。
4 结束语
针对传统的车辆转弯制动横向轨迹控制方法存在车辆整体滑移率较高、控制后的车辆滑行时间较长、滑行路程较远的问题,本文提出基于增强学习的车辆转弯制动横向轨迹控制方法。通过仿真验证了本文方法的有效性,解决了传统方法存在的问题。但在此设计中,由于时间与技术的约束,存在部分的不足。在日后的研究中,将根据应用中的不足进行合理优化,以此保证车辆的控制效果,提升交通安全性。
