基于CK-means算法的用户用电负荷聚类分析
2021-11-17程江洲
程江洲,何 艳,鲍 刚,潘 飞
(三峡大学电气与新能源学院,湖北 宜昌 443000)
1 引言
随着我国电力市场的进一步改革,许多电力公司都想研究消费者的需求行为,提高服务质量。掌握用户用电行为的信息,快速响应市场变化、客户多样化及个性化用户需求,可为实时或现货市场的参与者提供准确的需求侧管理算法[1]。本文旨在通过两种无监督学习方法的结合,并利用最大加权乘积法改进阈值不确定的问题,总结用户用电负荷曲线的特征,并计算代表每个聚类组的基线负荷[2]。
现代电力系统正朝着更可持续的方向发展,导致电网侧积累了海量数据,由于现有聚类分析技术算法单一不可避免地降低了数据的利用率[3]。文献[4]提出一种基于聚类结果的评价指标及复杂程度的来确定K-means算法的初始中心及聚类数目的方法。文献[5]提出一种新的分布式聚类方法,基于自适应K-means算法对海量用户的用电特性进行感知分析。文献[6]提出一种改进的K均值算法,引入Kl指数来确定最优聚类中心点来完成聚类分析,提取出典型用户用电负荷曲线。文献[7]提出了一种数据采样和K均值预聚类的方法,首先通过多次数据采样并采用K均值算法生成聚类结果,其次计算聚类结果的交集来构造加权连通图,最后得到聚类中心。然而,该方法缺乏对数据集总体样本分布的考虑,具有一定的局限性和不稳定性。文献[8]提出用AP算法确定聚类数K上限的方法,但没有给出确定最佳K值的具体方法。文献[9]中提出用K-means-u*算法来改进K-means++算法的局限性,但算法变得更复杂且不适用数据量过大的领域。K-means算法作为一种常用的聚类算法,其因操作简单、原理易懂,广泛被应用于聚类分析领域[10]。但其也存在以下问题:必须事先明确聚类数K值的大小、对初始聚类中心的选取要求高、容易收敛到局部最优解,导致错过全局最优解。
综上,为了克服上述问题,国内外学者将多种聚类算法进行结合,做到互补互助扬长避短[11]。本文首先对样本密度的K-means聚类方法进行基本描述,较改进前算法分析对比可知数据集的最优值K和初始聚类中心由密度冠层算法获得,可作为K均值算法的输入参数,解决了K值的确定和初始聚类中心的选择这两个难题;最后为了验证该模型,选取江西某地的216名用户为期一个月的负荷数据进行仿真,通过与两种典型的聚类方法进行比较,并用不同的有效性指标来评价它们的聚类性能,实验结果证明,改进后的新算法在准确性、稳定性和有效性方面都优于其它算法。
2 CK-means算法
2.1 Canopy算法原理
Canopy算法作为一种无监督的预聚类算法,常被用作K-means算法或层次聚类算法的预处理步骤[12],具体步骤如下:
步骤1:给出数据集D={X1,X2,….,Xn},设置阈值T1和T2,其中T1>T2
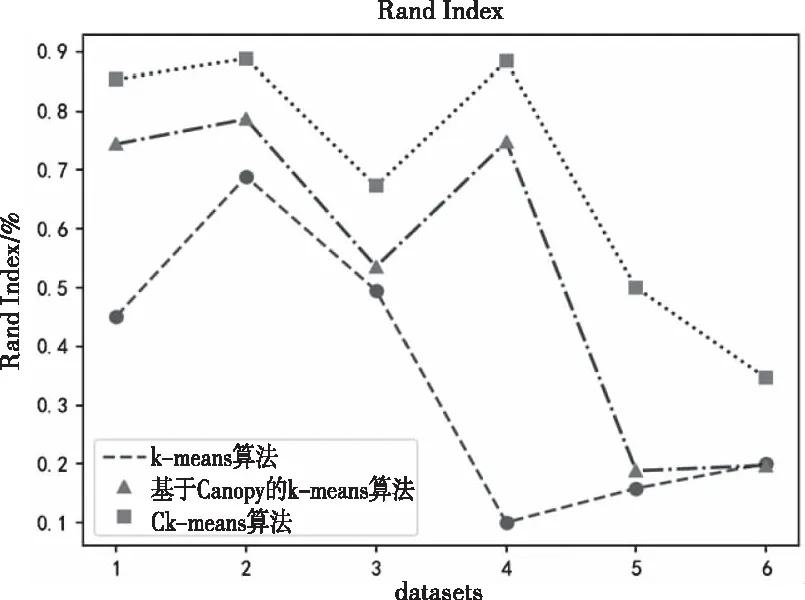
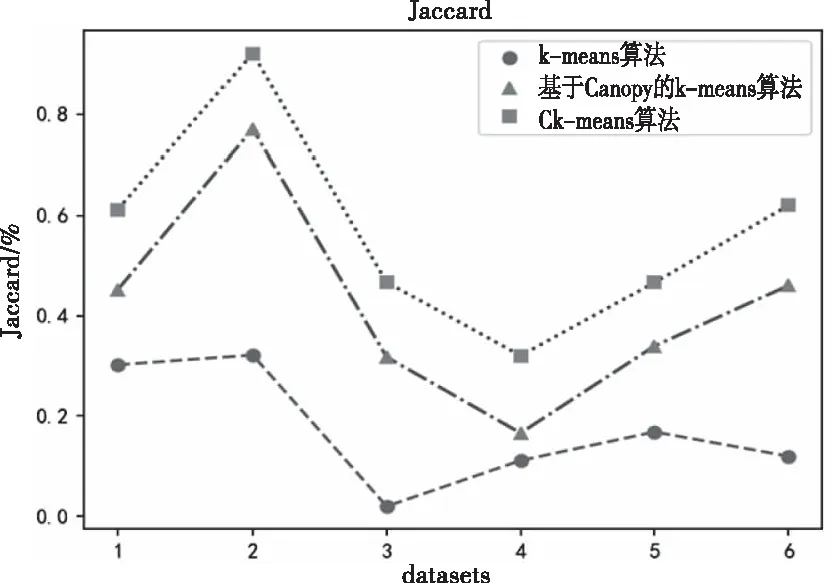
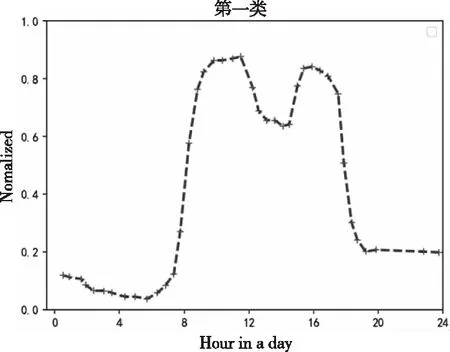
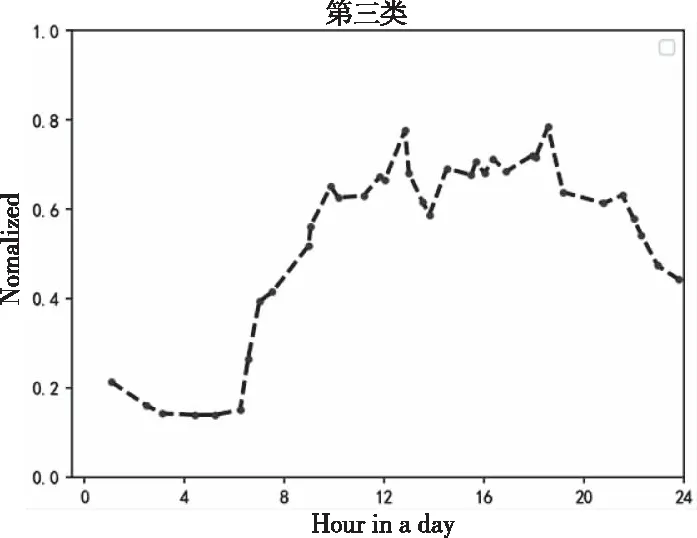
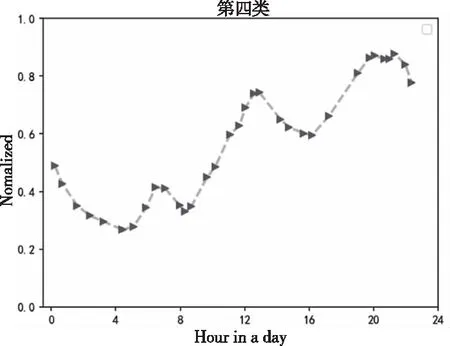
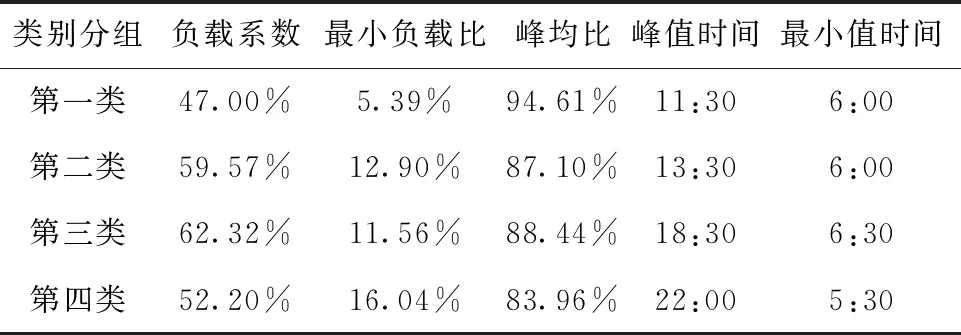
步骤2:从数据集D中提出样本点S,分别计算剩余样本点与点S之间的欧氏距离d。如果d 步骤3:完成计算出的d与T2的比较。如果d 步骤4:重复步骤2和步骤3,直到D为空。 但由于算法中T1和T2的阈值难以确定,阈值的大小对聚类结果影响很大[13]。因此,本文考虑引入密度参数来解决这个问题。 2.2.1 基础概念 对于给定的数据集D={X1,X2,….,Xn},则D中的样本元素m记为Xm={Xm1,Xm2,…,Xmr},1≤m≤n,其中r为Xm的属性数,d(Xp,Xq)表示两个元素Xp={Xp1,Xp2,…,Xpr}和Xq={Xq1,Xq2,…,Xqr}; 1)计算D中元素集的平均距离 (1) 2)计算D中元素i的密度 (2) 3)ρ(i)满足上式(2)条件的元素个数。将符合条件的元素归为一个集合,计算集合内元素的平均距离为a(i) (3) 4)S(i)为簇距离,其表示元素i(密度值较大点)与其它元素j的距离。若ρ(j)<ρ(i),则S(i)为max{d(i,j)};若有ρ(j)>ρ(i),则定义为min{d(i,j)},即 (4) 5)若D被分成k组,其中聚类的中心是Cj(j≤k)。聚类结果的平方误差之和E表示簇集中的样本点与其聚类中心的距离平方差之和,即 (5) (6) 如果ρ(i)值越大,表示i点附近聚集的样本点越多、样本点的分布更密集;a(i)值越小,1/a(i)的值就越大,这代表簇中的样本点就越紧密;S(i)值越大,两个聚类的相异程度越大。 2.2.2 算法流程 传统Canopy算法因阈值是随机选定导致聚类结果存在不稳定[14],因此本文提出最大加权乘积法来确定最优划分中的最佳聚类数以提高负荷聚类精度,其具体步骤如下: 步骤1:在给定数据集的情况下,参照式(2)计算所有样本的密度。选择密度最大的样本C1作为第一聚类中心,将中心C1加到集合C中,即C={C1}。同时,将所有满足剩余样本与第一聚类中心距离小于MeanDis(D)条件的样本从数据集中剔除; 步骤2:计算剩余数据集中样本的ρ(i)、a(i)和s(i),根据最大加权乘积法确定第二聚类中心C2,并将该中心加到集合C中,从而C={C1,C2}。同样,所有满足规定条件的样本都将从数据集中移除;最大加权乘积法求最优聚类中心的示意图如图1所示。 图1 最佳聚类中心的示意图 步骤3:重复步骤2,等D中无样本点后结束。 最后,数据集D被分成成K个簇集,若选取簇集中所有样本点距离的平均值作为聚类中心,可得到最优区分内的最佳中心数。 本文采用一种基于密度Canopy的k-means算法,本文称之为Ck-means算法。利用算法对数据集D进行初始预处理,可得到最优簇集K和最优聚类中心点,将其代入K-means算法中可提取出典型的用户用电负荷模式。改进后的CK-means算法可改善传统K-means算法存在的对初始聚类中心敏感、需要预先给定K值、弥补因阈值不确定造成结果不稳定的问题。 如图2所示,CK-means算法的执行流程如下: 图2 CK-means算法流程图 步骤1:引入样本点的密度参数,通过对Canopy算法的优化,可得到了最优的K值和初始聚类中心并将其作为K-means算法的输入; 步骤2:计算剩余数据集D中的样本点与初始聚类中心之间的欧几里得距离,并根据最小距离原则将负荷数据添加到相应聚类中心的簇集中; 步骤3:计算簇中元素的平均距离,并将该点取为新的聚类中心; 步骤4:将更新后的聚类中心与原聚类中心进行比较,若聚类中心点不再变化,则算法运行完毕,得到最终的聚类结果,否则返回步骤2。 本文以江西某地区的一个月用电数据进行仿真测试,选取该地区216名用户在2015-7-01至2015-8-01之间每日的96点负荷数据。数据集有646981条数据记录,每条包含3个数值型字段。 1)数据获取 删除空缺值,保证后期数据的运算。 2)数据归一化 鉴于每个用户一天中的最大负荷不同,对用户用电负荷数据进行归一化处理,得到进行聚类分析的数据集合。数据归一化的公式如下所示 (7) 其中:X代表用户的负荷数据,下标i代表用户的编号数、j代表0-23之间的数,代表了一天的96个节点时间;min和max分别某用户每日符合的最小值、最大值。 经过上述数据预处理,可绘制出当日不同时间不同用户的用电特征曲线,随机选取某用户在7月10日的负荷曲线图如图3所示。 图3 用户负荷曲线图 未经过聚类处理的数据比较杂乱,完全看不出规律,下面将当前获得的数据用传统的k-means算法与改进的CK-means算法分别进行聚类。其中为了更好地展示出聚类效果,选取了以下的评价指标:聚类分析时间T、聚类结果的误差平方差之和E以及衡量聚类有效性的三个参数:Rand指数、Jaccard系数和聚类精度。在表1中比较了k-means算法、Ck-means算法在数据集上的聚类结果的平方差E和聚类时间T(s)。 根据上表所示,可得出以下结论: 1)K-means算法完成数据聚类的时间较长。由于其初始中心点是随机选取的,那么算法就需要经过多次迭代后结果才能稳定,因此执行的时间会比较长;基于Canopy的k-means算法因阈值不确定导致结果存在不稳定性;新改进的算法可提前确定K值和初始聚类中心,并将其作为k-means的输入参数从而完成对数据集的聚类。新算法迭代次数少,故会比传统算法效率更高。 2)从误差平方和E来看,Ck-means算法的聚类效果最好。由于K-means算法的初始聚类中心是随机选取的,基于Canopy的k-means算法的聚类结果存在不稳定性,因此上述两种算法计算出的E较大且聚类结果也不理想。 3)聚类质量评价指标 本文将添加六组模拟的数据集进行训练,用于测试改进算法对较大数据集聚的类效果,测量聚类结果的评价指标(聚类精度Accuracy、Rand指数和Jaccard系数)对比图如图4-图6所示。 图4 聚类精度 图5 Rand 指数 图6 Jaccard系数 对比图4-6的参数对比图可知,改进算法的三个参数都是最优且准确率最高[15]。此外,该算法的聚类精度比传统K均值算法高31.6%,比基于Canopy的K均值算法高6.2%。 本文所提出的CK-means算法首先是把数据集D的密度算出来,找到数据集中最紧凑的聚类,利用最大乘积加权来确定初始聚类中心,从而确定最优值K=4。综上所述,新算法的聚类结果更准确、收敛速度更快,可实现聚类结果全局最优化[16]。 3.4.1 负荷曲线分析 基于CK-means算法的负荷数据聚类分析中,模型将用户分为四个类别,其中第一类中含26个用户、第二类中含82个用户、第三类中含97个、第四类中含10个用户。第一类用户属于典型的双高峰用户,这意味着其大部分功率在高峰时间内消耗。图7、图8的曲线趋势类似,明显属于高峰时间内的消耗行为,但不同的是,与前图相比,图8中的最小负载峰均比有所提高。 图7 第一类用户 图8 第二类用户 图9 第三类用户 图10 第四类用户 由图9可知,第三类用户属于白天高峰用电型。由于其两峰值之间的谷值负载基本被填充,表明部分负载已由高峰期转移到其它时间。第四类用户属于典型的夜间用电型,其非高峰时段为3AM-12 AM和3PM-5 PM,这表明其用户可能有很大的潜力遵循需求侧管理策略来避免高峰期的用电行为。 3.4.2 聚类用户特征总结 由表2可知,第一类用户的负载系数最低、负荷比最小以及最高峰值与最小值的比值最大;第一、二类用户有着相似的双峰值负载,但第二类用户负载峰值与最小值的比值较小,这表明与第一类用户相比,其需求侧管理的潜力较小。而第三类与之前两种曲线对比的话相对更平滑,因其负载曲线的趋势不同,最高峰值时间和最低峰值时间与前者也有所不同。第四类用户的峰值时间不同,这表明与其它类用户相比,更有利于解决不同用户之间的需求侧管理。 表2 聚类用户特征总结 本文提出一种基于CK-means算法的用户用电负荷聚类分析方法。首先使用密度Canopy算法对用户用电数据进行预处理,可得到最优簇集值K与最佳初始聚类中心,然后将其代入K-means算法中可提取出典型的用户用电负荷模式,研究结果如下所示: 1)CK-means算法同时保持了Canopy的特点及传统K-means算法精确高效的特点; 2)采用最大加权法可显著提高聚类结果的精确度; 3)该算法可以弥补Canopy因阈值T1、T2不确定造成的网络收敛时间过长; 4)该算法解决了传统的K-means算法因初始聚类中心选取不当将导致聚类效果不佳的问题。 综上所述,该算法解决了传统算法存在的聚类时间过长、准确率过低的问题,可提高用户分类的可靠性和有效性。基于聚类结果,可为负荷预测、电力营销策略、用户筛选识别等提供有效的参考。2.2 基于密度的Canopy算法
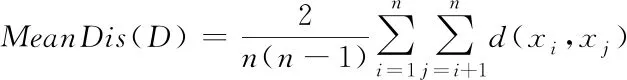
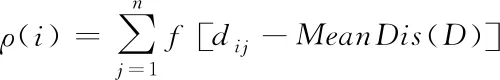
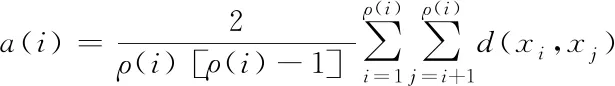
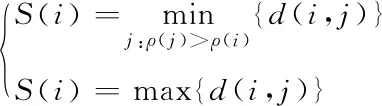


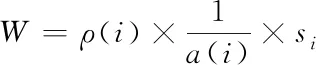

2.3 CK-means算法
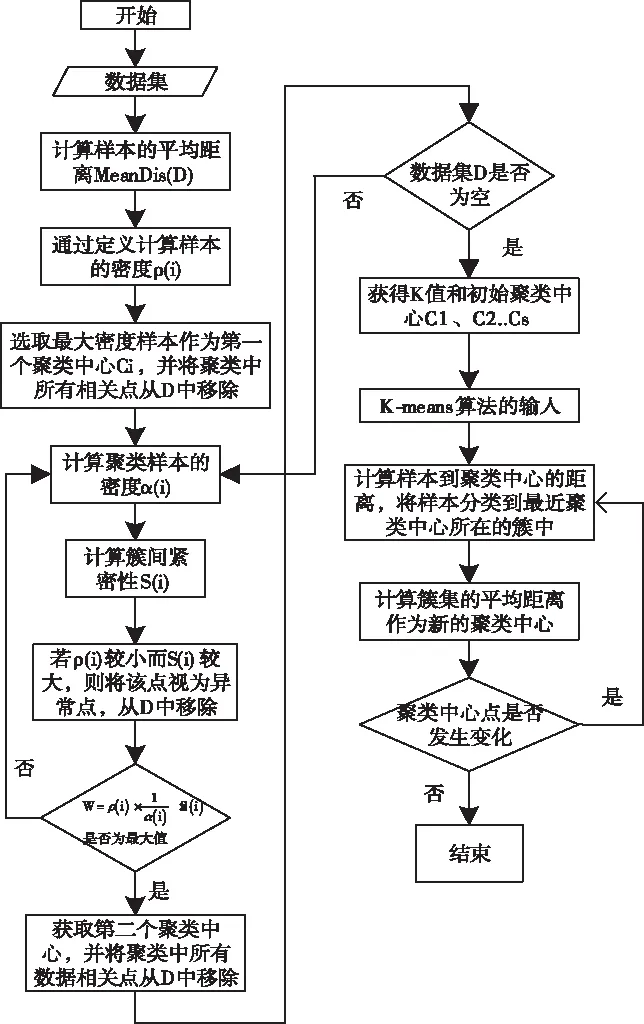
3 实例验证分析
3.1 数据集
3.2 数据预处理

3.3 聚类算法对比分析
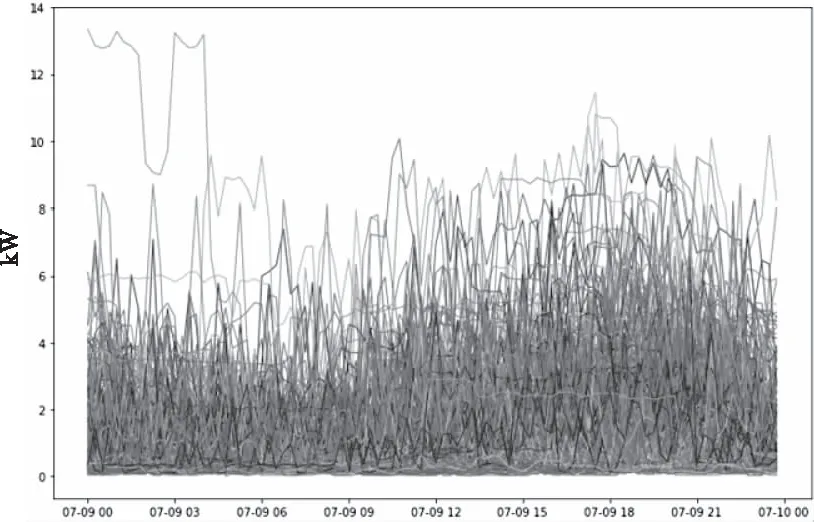
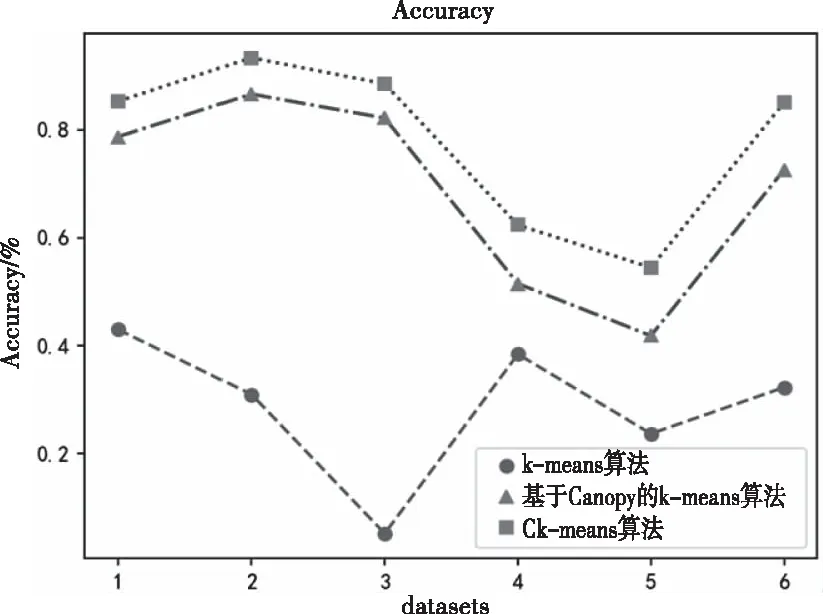
3.4 特征分析

4 结论
