悬立式深海钴结壳采矿头的参数化设计与优化

赵 波，赵海鸣，刘 晨，胡 刚

（中南大学机电工程学院，湖南长沙 410083）

钴结壳又称富钴锰结壳，其所蕴含的金属资源对未来高科技领域的发展具有重要的战略意义[1]。钴结壳一般分布在400～4 000 m深的海底，其中太平洋海域内的厚层钴结壳广泛分布在800～2 500 m深的海山斜坡或无沉积物覆盖的海山山顶附近[2]。钴结壳矿区不同于其他的多金属结核矿区：不仅矿层厚度的变化较大，表面的地貌特征也很复杂，这对采矿头的设计提出了较高的要求。目前，钴结壳采矿头的设计主要采用螺旋滚筒式结构（参照采煤领域内应用较为成熟的滚筒式采煤机）[3-4]，其相较于拖刀式、圆盘式或水射流式等结构在能耗方面具有一定的优越性[5]。螺旋滚筒式采矿头具有破碎能力强、稳定性高等优点[6]，但其在实际开采过程中存在很大的局限：由于难以适应复杂的地势起伏，使得开采时会有较多的废石混入。为此，笔者基于螺旋滚筒式采矿头，设计了一种能够适应不同地貌特征且姿态可调的悬立式采矿头，并对其参数进行优化，使其更符合实际开采的工况要求，以便能在复杂多变的海底矿区实现对钴结壳的精准开采。

1 悬立式采矿头参数化设计

1.1 采矿头工况及设计要求分析

海底钴结壳矿床分布的覆盖范围及钴结壳丰度与矿床表面形态和海底地貌密切相关。由于受到火山运动、沉积作用及海底层流等因素的影响，钴结壳矿床的出现往往伴随着错综复杂的地貌特征。其中，一种典型的地貌为连绵的火山熔岩上生长着起伏度为0.5 m左右的矿层，并在山顶的宽鞍部及山的外缘阶梯上发育明显，与薄层沉积物交替出现[2，7]，如图1（a）所示。根据海山坡度与矿石丰度的相关研究，为保证可靠的采矿作业以及良好的经济效益[8]，一般选择坡度小于15°的钴结壳矿床。另外一种典型的地貌为小范围的沟槽地势，沟槽的垂直落差大于10 cm[9]，主要分布着鹅卵石状的钴结核及大块的砾状钴结壳，并有大量沉积物覆盖，如图1（b）所示。

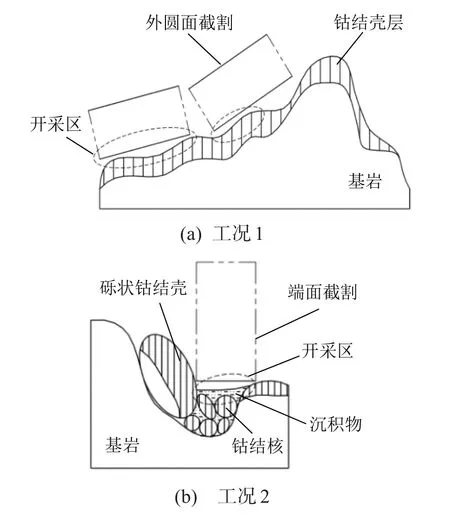
图1 钴结壳开采的典型工况示意Fig.1 Schematic diagram of typical working conditions of cobalt crust mining

综合上述2种典型的地貌特征，为了实现钴结壳的精准剥离，采矿头的设计须满足以下2个基本要求：一是当采矿头采用外圆面进行大面积截割时，可沿宽度方向偏转；二是针对小范围的沟槽地势（允许的最大直径小于采矿头的宽度），为了保证开采的高效性，采矿头一侧端面能参与截割。此外，为了使采矿头在姿态调节的过程中能均匀、连续地截割矿石，可将圆柱形轮廓设计成带有一定锥度的圆台形状，并在端部采用弧形面过渡。这样既有利于采矿头端面截割时碎屑的排出，又能使采矿头在用外圆面截割时更好地贴合矿床的小角度斜坡地势，提高开采率。考虑到深海环境下开采工况较为恶劣，采矿头端部的过渡弧形面应尽可能平缓，并在端部预留足够的空间，以减少截齿之间的干涉，从而避免制造困难[10]。因此，本文设计的悬立式采矿头选用椭球面作为端部过渡弧形面。悬立式采矿头体的轮廓如图2所示。

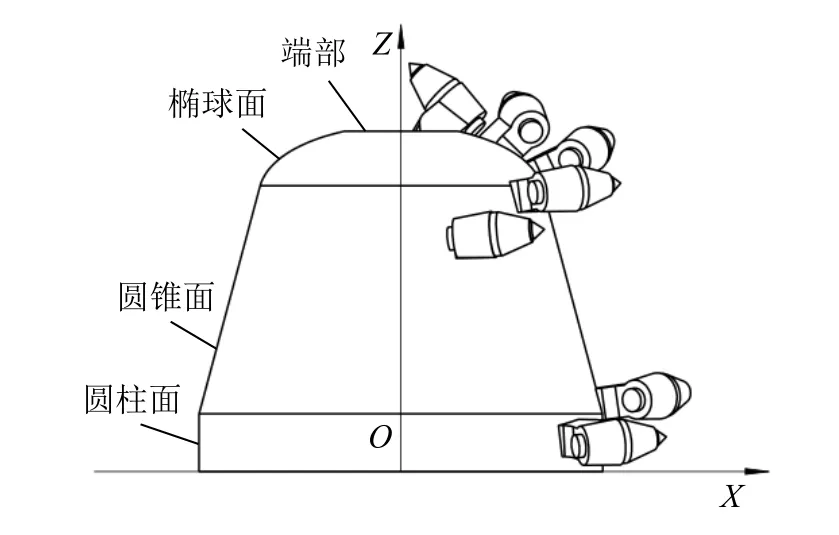
图2 悬立式采矿头体的轮廓示意Fig.2 Schematic diagram of outline of suspended mining head body

1.2 采矿头螺旋线设计

为了获得最佳的钴结壳破碎效果，悬立式采矿头体上的截齿采用螺旋式布置方式。但采矿头体上的截齿排布螺旋线条数不宜过多，否则难以保证破碎过程中参与截割的截齿数恒定。实践证明，钴结壳采矿头体上的截齿排布螺旋线为2或3条最为常用[11]。螺旋线可看作空间一点绕截齿齿尖包络面作回转运动并沿竖直方向平移所形成的轨迹，而包络面可看作采矿头体一侧的轮廓线偏移一段距离后所形成的曲线绕中心轴OZ旋转而成的曲面，如图3所示。图3中：c为椭球中心的纵坐标；s1、h1分别为包络面上椭球弧与圆锥面轮廓线分割点的横、纵坐标；D为包络面的大端直径；s为包络面上圆柱面轮廓线与圆锥面轮廓线分割点的纵坐标。

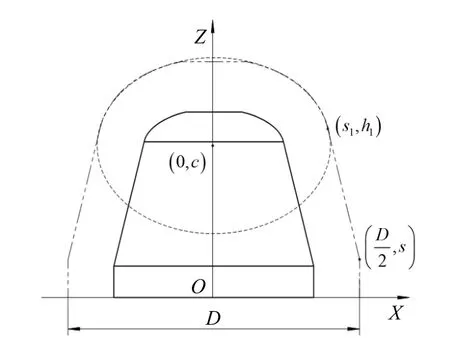
图3 悬立式采矿头体的包络面旋转曲线示意Fig.3 Schematic diagram of envelope surface rotationcurve of suspended mining head body

根据图3所示的包络面旋转曲线的分割点坐标以及椭球段的曲线方程（其中h≤1z≤c+a，a、b分别为椭球段长轴和短轴的长度），可得到不同包络面上螺旋线的参数方程。

式中：λ3为椭球面螺旋线的导程，mm。

为了保证破碎过程的连续性，要求不同包络面上每条螺旋线的螺旋升角为定值，以改善截齿的截割条件[12]。其中，螺旋升角ψ可定义为螺旋线上一点绕中心轴OZ旋转所形成的圆弧的切线与在其竖直平面内投影轨迹切线之间的夹角，如图4所示。

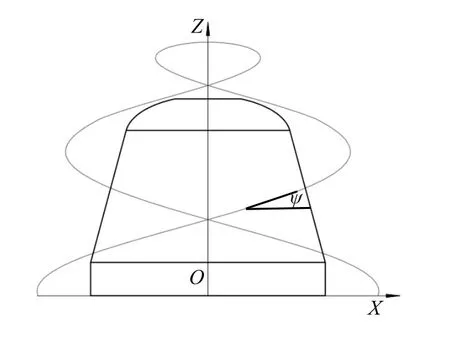
图4 螺旋升角示意图Fig.4 Schematic diagram of helix angle

由图4可知，螺旋升角的计算式为：

式中：λ为螺旋线的导程，mm；d为轨迹初始点绕中心轴OZ旋转所形成的圆弧的直径，mm。

对于悬立式采矿头，其不同包络面上螺旋线的导程满足λ1/D=λ2/2=λ3/2s1时，才能保证螺旋升角ψ为定值。此外，螺旋开角ψ不宜过大，否则截齿的排布较为稀疏，易加剧截齿的磨损。

1.3 截齿的空间位置确定

考虑到采矿头主要用于剥离相对较薄的钴结壳层，故截齿齿尖在螺旋线上的排布多采用顺序式[13]。此种排布方式能保证截齿依次并规则地切入矿石，从而提高开采率。结合图1可知，当悬立式采矿头的外圆面参与截割时，圆柱面与圆锥面作为主切削面，截齿采用等截距布置方式；当悬立式采矿头的端面参与截割时，椭球过渡面与端面作为主切削面，截齿采用不等截距布置方式，且截距从靠近矿石的一侧向另一侧逐渐增大，以尽可能使截齿承受相同的载荷。截齿在采矿头体上的空间位置受到其安装角μ与倾斜角ε的影响。

为确定悬立式采矿头体上截齿的空间位置，任意选取一颗截齿为对象，以其中心线上的某一点为原点，建立局部坐标系O1-X1Y1Z1（其可看作由坐标系O-XYZ沿Z轴旋转及平移所得），如图5（a）所示；局部坐标系O1-X1Y1Z1下截齿中心线O1P（P点为截齿齿尖端点）的空间位置如图5（b）所示，其中面PAFE在截齿齿尖端点P与采矿头中心轴OZ所构成的平面内。安装角μ为截齿中心线O1P在垂直于采矿头中心轴OZ的平面上的投影DP与截齿齿尖运动轨迹切线PC之间的夹角；倾斜角ε为由截齿中心线O1P与截齿齿尖运动轨迹切线PC所确定的平面与垂直于采矿头中心轴OZ的平面之间的锐角；截割角δ为截齿齿尖运动轨迹切线PC与截齿中心线O1P之间的夹角。

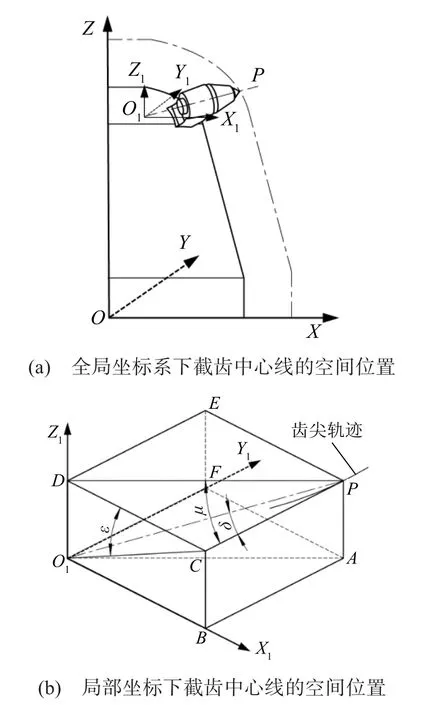
图5 不同坐标系下截齿中心线的空间位置Fig.5 Spatial position of pick centerline under different coordinate systems

由图5可得：

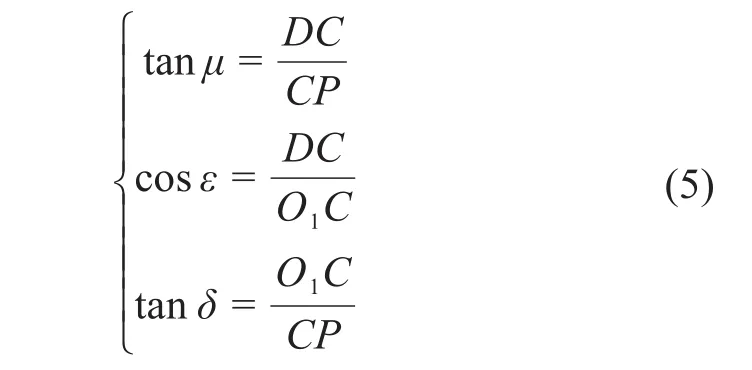
由此可得，安装角、倾斜角与截割角之间的转换关系为tanμ=cosε⋅tanδ。当ε和μ确定时，即可确定面O1CP与面O1DPA的位置，这2个面的相交线即为截齿的中心线，由此可确定截齿的空间位置。

2 悬立式采矿头参数优化

在钴结壳开采过程中，采矿头是主要部件，其消耗了整辆采矿车80%以上的功率。采矿头体上截齿的排布参数直接影响单个截齿的受力[14]，同时采矿头的结构参数和工作参数会影响整辆采矿车的生产效率及能耗。因此，为了获得最佳的钴结壳破碎效果，对悬立式采矿头的关键结构参数和工作参数进行优化，以使其符合工程实际应用场合的要求。

2.1 优化变量选择

对所设计的悬立式采矿头的截割性能影响较大的结构参数主要为截齿齿尖包络面的大端直径D、截齿齿尖截距td、采矿头圆锥段的轴向长度L、采矿头体的半锥角ξ和截齿安装角μ。此外，采矿头的工作参数（如转速n、牵引速度vq和截割深度h）也会直接影响整个开采过程的工作效率。因此，选择上述参数作为优化变量，表示为：

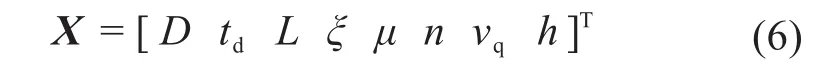
2.2 优化目标确定

为了符合实际开采过程中的经济性要求，以采矿头破碎单位体积钴矿石所消耗的能量最小为优化目标。为获得截齿在截割过程中的能耗模型，建立悬立式采矿头体上截齿的截割阻力与截割速度的关系，如图6所示。图中：Fn为截齿的截割阻力；vj为采矿头的截割速度；vn为截齿齿尖的合速度；Ft、Fr分别为截齿齿尖受到的切向阻力和径向阻力；η为同一条螺旋线上相邻2颗截齿齿尖之间的圆周角；φ为截割深度为h时截齿齿尖与钴结壳接触圆弧的半周角；θM（M为与同一时刻参与截割的截齿数量有关的参数，M=0，1，…，Mm，其中Mm为不超过2φ/η的最大整数）为截齿齿尖端点与采矿头旋转中心的连线与X2轴正方向之间的夹角；γ为采矿头截齿齿尖的合速度vn与X2轴负方向之间的夹角；α为切向阻力Ft与截割阻力Fn之间的夹角。

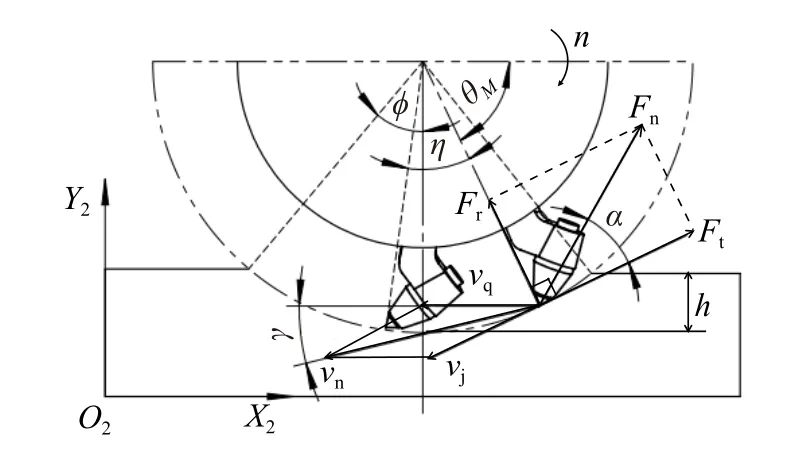
图6 悬立式采矿头体上截齿的截割阻力与截割速度的关系Fig.6 Relationship between cutting resistance and cutting speed of pick on the suspended mining head body

研究表明，截齿截割钴结壳的特性与截割中等强度煤岩相似且截割机理相同[15]。参考成熟的采煤理论，可得截齿截割钴结壳时所受的阻力为：

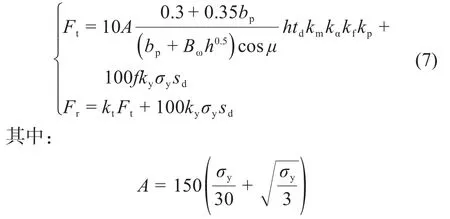
式中：A为钴结壳的平均截割阻抗，N/mm；σy为钴结壳的单轴抗压强度，MPa；bp为截齿接触钴结壳部分的等效宽度，cm；Bω为钴结壳的脆性程度指数；km、kα、kf和kp分别为钴结壳的裸露系数、截割角的影响系数、截齿前刃面的影响系数和截齿的配置系数；f为截齿运动时的阻力系数；ky为平均接触应力与单向抗压强度的比值；kt为比例系数；sd为截齿的磨损面积，cm2。

由图6可得：

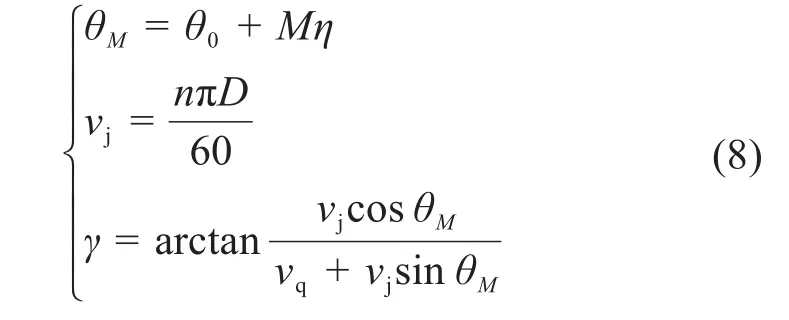
式中：θ0为截齿齿尖端点与钴结壳刚开始接触时与X2轴正方向之间的夹角，（°）。

采矿头在开采过程中的能耗主要分成两部分：一部分是截齿工作时克服截割阻力所消耗的能量Pj；另一部分是由于受到海水的黏性切应力作用，采矿头克服一定海水阻力所做的功Ph。因此，采矿头在破碎钴结壳过程中的比能耗Hω为：

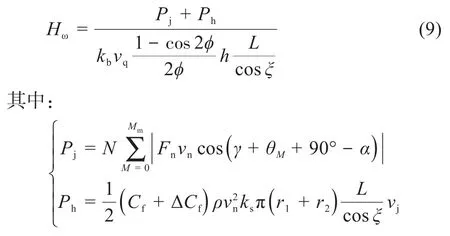
式中：N为螺旋线的条数；r1、r2分别包络面上锥段部分小端、大端的半径，m；kb为破碎过程中钴结壳的松散系数；ρ为海水密度，kg/m3；Cf为摩擦阻力系数，与雷诺数相关；ΔCf为粗糙度补贴系数；ks为表面形状效应修正因子。

2.3 约束条件

1）截齿安装角。在理想状态下，安装截齿时应尽可能使其齿尖所受合力的方向与截齿中心线重合，以减小截齿所受的弯矩。但在实际截割过程中，截齿齿尖以一定的角度切入矿石，易对矿石产生干扰，致使齿身与未被截落的钴结壳发生干涉，两者相互挤压、摩擦，从而导致截割阻力增大，加剧了截齿的磨损[16]。因此，在确定截齿的安装角时应综合考虑截齿的几何参数以及钴结壳矿石的性质。如图7（a）所示，截齿以安装角μ切入矿石，此时其齿尖部分的投影视图如图7（b）所示。

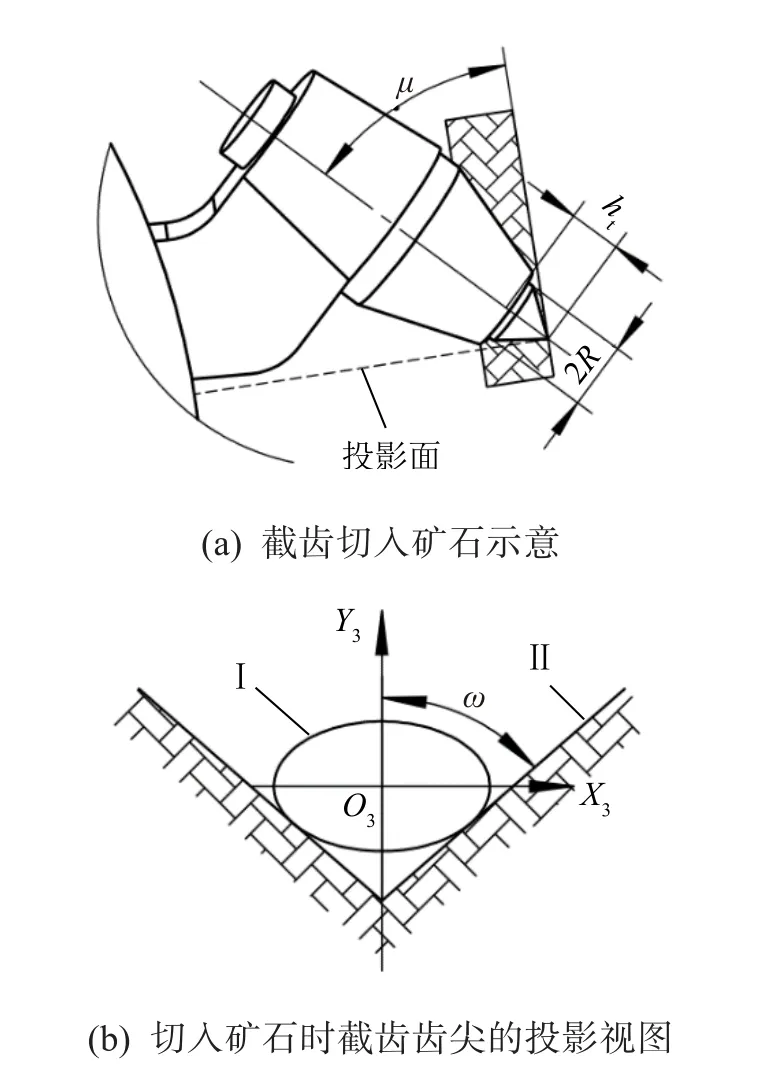
图7 截齿切入矿石的示意及其齿尖的投影视图Fig.7 Schematic diagram of pick cutting into ore and projection view of pick tip

基于图7，截齿齿尖圆弧线和钴结壳崩落线的投影曲线I、Ⅱ的方程可表示为：

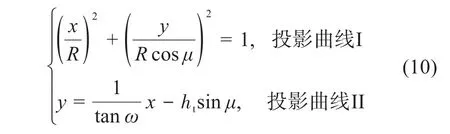
式中：R为截齿齿尖的半径，mm；ht为截齿齿尖的高度，mm；ω为钴结壳的崩落角，（°）。

投影曲线I和Ⅱ相切时为截齿与钴结壳矿石不发生干涉的临界状态，相离时为不发生干涉。联立2条曲线的方程可得，截齿与钴结壳矿石不发生干涉的约束条件为：

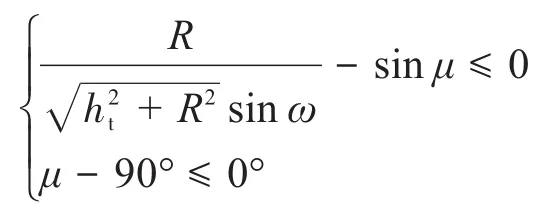
2）截齿齿尖的截距。截齿齿尖的截距是影响采矿头破碎效果、功率消耗及截割效率的重要参数。若截距太大，则成形截槽之间的裂纹无法交汇，从而导致矿石无法被有效开采；若截距太小，则破碎后的矿石太碎，从而导致截割效率降低。因此，应合理选取截齿齿尖的截距。当悬立式采矿头的旋转轴线以与水平方向成ξ的姿态破碎钴结壳矿石时，其截齿齿尖的截距如图8所示。

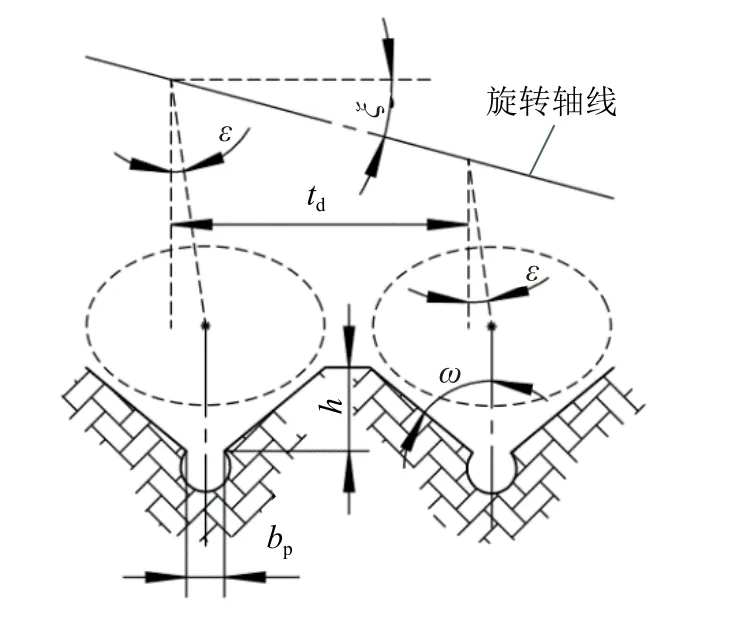
图8 截齿齿尖截距示意图Fig.8 Schematic diagram of intercept between pick tips

由图8可得，截齿齿尖截距的约束条件为：

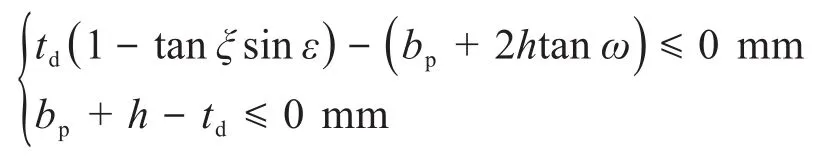
3）牵引速度。为了取得良好的经济效益，钴结壳产能须达到要求，则采矿头的牵引速度不能太小。有资料指出，钴结壳矿区开采量在100万t以上时才具有商业开采价值，且在海面上工作的采矿系统的正常使用时间应大于65%[5]。同时，考虑到钴结壳破碎过程的稳定性，采矿头的牵引速度不宜太大，应小于0.5 m/s[17]。由此可知，采矿头牵引速度的约束条件为：

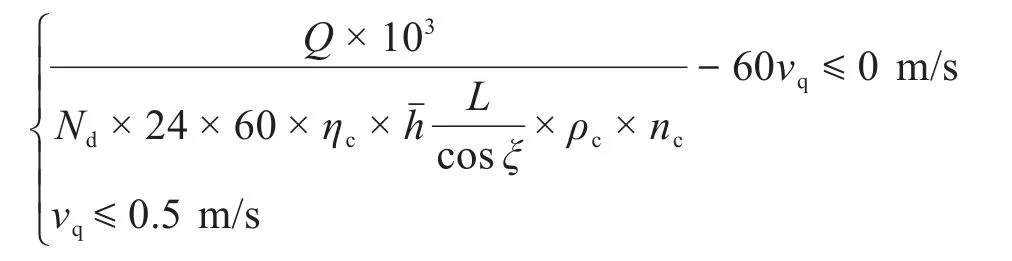
式中：Q为钴结壳的年产量，t；Nd为工作时间，d；ηc为开采效率为具有开采价值的钴结壳层厚度，m；ρc为钴结壳的干密度，kg/m3；nc为采矿头的数量。

4）包络面大端直径。包络面大端直径是确定采矿头尺寸的重要参数。若包络面大端直径太小，则不仅会增加采矿头工作的循环次数，而且不利于端部截齿的布置；若包络面大端直径太大，则会消耗较大的能量，不利于钴结壳层的破碎。包络面大端直径主要受采矿头圆锥段小端部分尺寸以及采矿头工作时的最大功率的限制，其约束条件为：

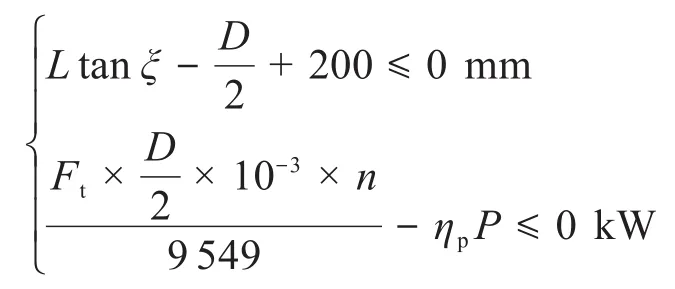
式中：ηp为采矿头动力系统的传递效率；P为采矿头工作时的最大功率，kW。

5）其他约束。采矿头转速n会影响矿石粉末的产生及截齿的使用寿命，在保证一定的开采率的条件下，其约束为36 r/min≤n≤100 r/min。采矿头圆锥段的轴向长度L主要受结构尺寸的约束，其约束为L≥180 mm。采矿头的半锥角ξ与钴结壳分布的地势坡度有关，其约束为10°≤ξ≤25°。采矿头的截割深度h与薄层钴结壳厚度和极限切削厚度有关，其约束为10 mm≤h≤140 mm。

2.4 优化求解

上文建立的悬立式采矿头参数优化模型属于非线性约束模型，因此采用能在设计变量空间内通过多点搜索求得全局最优解的遗传算法进行求解。将目标函数、约束条件写入m文件，编写遗传算法运行的主函数并在MATLAB中提交运行，由此计算得到一组适应性最佳的悬立式采矿头结构参数和工作参数，如表1所示。

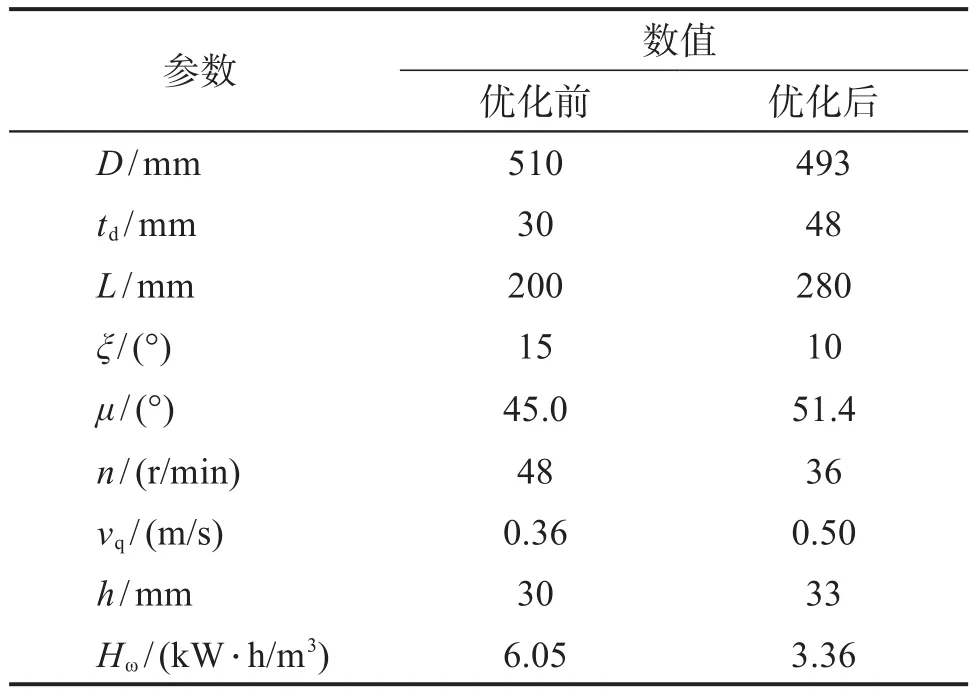
表1 优化前后悬立式采矿头的结构参数和工作参数对比Table 1 Comparison of structural parameters and working parameters of suspended mining head before and after optimization

由表1可知，相比于优化前，优化后悬立式采矿头破碎钴结壳的比能耗约降低了44%，截距约增大了60%，圆锥段的轴向长度约增大了40%，牵引速度约增大了39%。由此可得，适当增大截距能有效降低悬立式采矿头破碎钴结壳的比能耗。同时，在满足负载功率的条件下，适当增大采矿头的牵引速度与轴向尺寸不仅能提高开采效率，还能降低破碎过程的能耗。

3 悬立式采矿头破碎钴结壳过程仿真分析

为了验证上述悬立式采矿头参数优化结果的准确性，借助数值仿真手段来分析优化前后采矿头破碎钴结壳的比能耗，并对破碎过程中的载荷波动系数进行对比。这样既能缩短研发周期，又能较好地评估采矿头的稳定性。考虑到ABAQUS软件在非线性优化问题分析方面具有一定的优越性，因此采用该软件中的显式动力学有限元方法对优化前后悬立式采矿头破碎钴结壳的过程进行数值模拟。

3.1 仿真模型建立

在实际开采过程中，悬立式采矿头受到的海水阻力所做的功远小于截割阻力所做的功。为了更好地分析采矿头破碎钴结壳的过程，对其仿真模型作如下简化处理：1）忽略海水介质对采矿头的影响；2）将采矿头体、截齿及其齿座当作一个刚性的整体，只考虑截齿齿尖与钴结壳的接触；3）将钴结壳层视为连续、均匀、各向同性的介质，并假设破碎后的矿石不参与后续过程。

基于优化前后悬立式采矿头的结构参数，分别建立采矿头三维模型，并用有限体积的长方体代替钴结壳层。考虑到钴结壳属于材质特殊的岩石，其破碎过程中的耗散能主要通过塑性变形及裂纹扩展等方式转化[18]，因此采用广泛应用于岩土分析领域的Drucker-Prager模型来构建其本构模型[19]。采矿头截齿齿尖采用硬质合金材质，由于其硬度、强度远大于钴结壳，将整个采矿头视作刚体，并将刚体的自由度耦合在设置的参考点上。钴结壳和悬立式采矿头的材料参数如表2所示[20]。

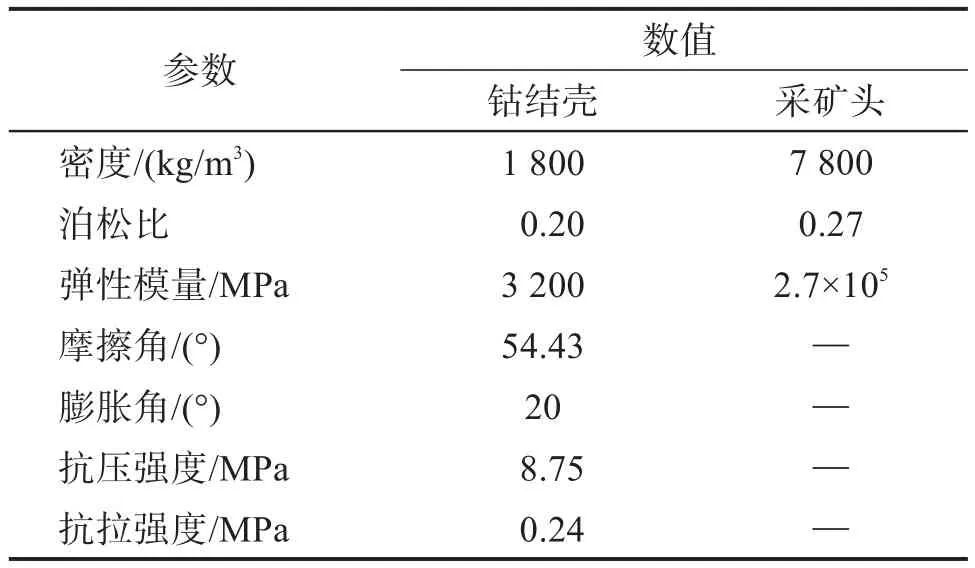
表2 钴结壳和悬立式采矿头的材料参数Table 2 Material parameters of cobalt crust and suspended mining head

根据优化前后的截割深度，分别调整悬立式采矿头相对钴结壳的高度，设置主从接触属性：法向作用为硬接触，切向作用的摩擦系数为0.2。同时，将钴结壳底面固定并对采矿头上参考点（采矿头圆柱部分中心）设置相应的转速和牵引速度，并通过设置不同的分析步长来保证优化前后采矿头的开采距离相同。由于采矿头整体结构复杂，选择四面体单元C3D10M对采矿头三维模型进行网格划分，选择六面体结构化单元C3D8R对钴结壳层模型进行网格划分，建立的有限元仿真模型如图9所示。

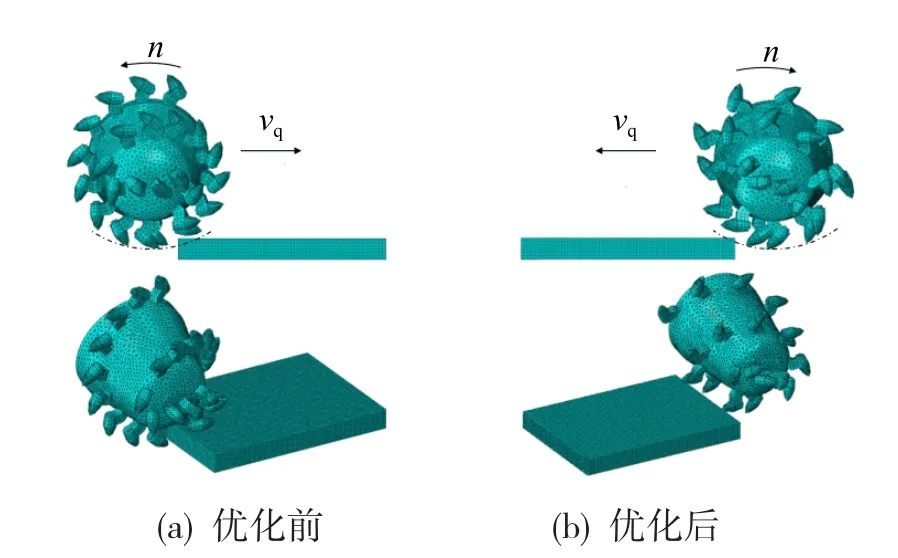
图9 优化前后悬立式采矿头破碎钴结壳的有限元仿真模型Fig.9 Finite element simulation model of crushing cobalt crust by suspended mining head before and after optimization

3.2 仿真与结果分析

通过仿真分析得到优化前后悬立式采矿头在破碎钴结壳过程中输出的总能量，如图10所示。由图10可知，优化后悬立式采矿头破碎钴结壳的用时较短，且输出的总能量较小。由采用优化前后悬立式采矿头破碎时钴结壳截面的塑性应变（见图11）可知，采用优化后采矿头破碎时钴结壳的塑性截面上未变形区域起伏较为明显，表明采用优化后采矿头破碎时仅少部分钴结壳未被有效剥离。

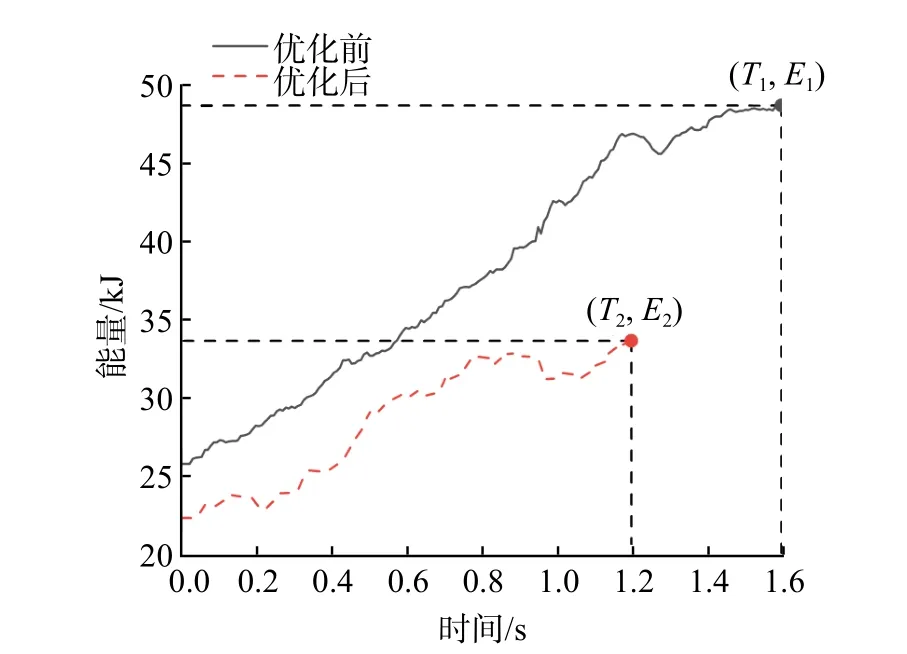
图10 优化前后悬立式采矿头在破碎钴结壳过程中输出的总能量对比Fig.10 Comparison of total output energy of suspended mining head during cobalt crust crushing before and after optimization

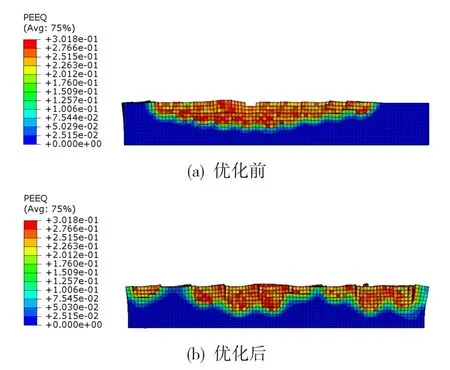
图11 采用优化前后悬立式采矿头破碎时钴结壳截面的塑性应变云图Fig.11 Plastic strain nephogram of cross section of cobalt crust crushed by suspended mining head before and after optimization

分别统计采用优化前后悬立式采矿头破碎钴结壳后失效网格的数量，并利用式（11）计算优化前后采矿头破碎钴结壳的比能耗仿真值，结果如表3所示。

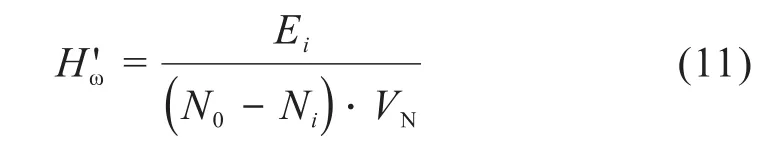
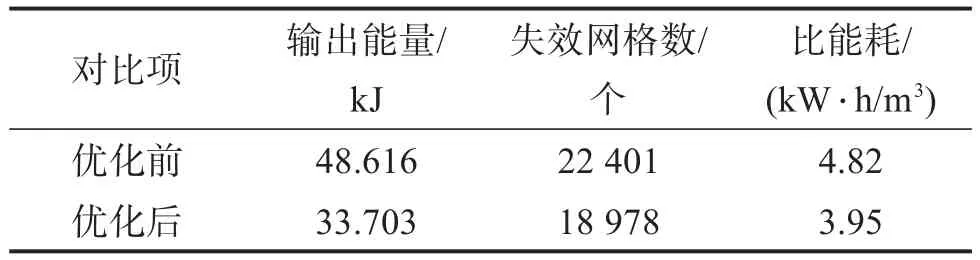
表3 优化前后悬立式采矿头破碎钴结壳的比能耗仿真值对比Table 3 Comparison of simulation values of specific energy consumption of crushing cobalt crust by suspended mining head before and after optimization

式中：Hω'为比能耗仿真值，J/m3；E（ii=1，2）为采矿头输出的总能量，J；N0为钴结壳层的初始网格数；N（ii=1，2）为破碎后钴结壳层残余的网格数；VN为单位网格的体积，m3。

由表3可知，优化后悬立式采矿头破碎钴结壳的比能耗相较于优化前降低了18%，与基于理论计算得到的相对误差44%有所差别。这是因为优化后悬立式采矿头的截距增大，钴结壳在截齿齿尖作用下产生的小裂纹更易与内部的层理缺陷相遇，从而发育成侧向裂纹，导致剥离的结壳块度增大。由于仿真选定的钴结壳本构模型是基于剪切损伤的理想弹塑性模型，其失效准则是基于积累的等效塑性应变，而真实钴结壳具有多孔的中硬脆性，因此仿真过程中钴结壳在接触的主区域发生变形失效但并未产生大区域的脆性断裂，从而导致钴结壳残留。由此可知，仿真得到的钴结壳破碎体积小于理论计算的，且由于优化后的悬立式采矿头易剥离钴结壳，使得优化后仿真得到的钴结壳破碎体积比理论计算的更小，从而导致仿真结果与理论计算结果存在偏差。

根据仿真结果绘制优化前后悬立式采矿头在破碎钴结壳过程中所受载荷的变化曲线，如图12所示。

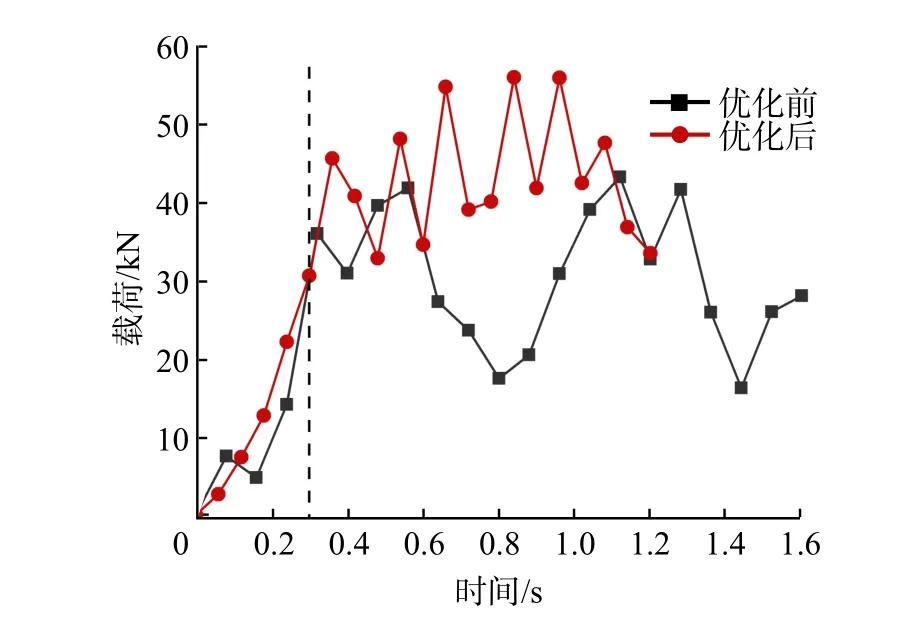
图12 优化前后悬立式采矿头在破碎钴结壳过程中所受载荷的变化曲线Fig.12 Variation curve of load on suspended mining head during cobalt crust crushing before and after optimization

为便于比较优化前后悬立式采矿头在破碎钴结壳过程中所受载荷的波动特性，引入载荷波动系数δf，其计算式为[21]：

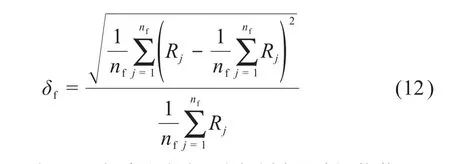
式中：Rj为悬立式采矿头在不同时刻所受的载荷，N；nf为悬立式采矿头承受载荷时的离散点数。

考虑到采悬立式矿头所受载荷从0 N开始增大，且破碎前期所受载荷对载荷均值影响较大，对波动特性无明显参考意义。因此，为了提高计算结果的可靠性，仅将0.3 s后悬立式采矿头所受载荷代入式（12），得到采矿头优化前后的载荷波动系数分别为28.1%和19.3%。结果表明，优化后悬立式采矿头所受载荷的波动系数较优化前降低了31.3%，说明优化后采矿头所受载荷的波动更小，更符合稳定性要求。

4 结 论

1）基于海底钴结壳分布的地貌特征，创新地设计了一种悬立式钴结壳采矿头。为建立悬立式采矿头参数化设计的数学模型，给出了其截齿排布螺旋线的方程以及截齿空间定位角之间的关系。

2）基于悬立式采矿头的设计方案，通过分析采矿头的实际开采工况要求，建立了以采矿头在破碎钴结壳过程中的比能耗最小为目标的优化函数，并以截齿不发生干涉、合理布置截距、钴结壳产能达标及最大功率限制等为约束条件，对所设计采矿头的主要结构参数和工作参数进行优化，并利用遗传算法计算得到一组最优解。理论计算结果表明，优化后悬立式采矿头破碎钴结壳的比能耗约降低了44%。

3）基于ABAQUS软件建立了优化前后悬立式采矿头破碎钴结壳的有限元仿真模型。通过仿真分析发现，优化后采矿头破碎钴结壳的比能耗较优化前降低了18%，且所受载荷的波动系数降低了31.3%，验证理论优化模型的有效性。

研究结果对钴结壳开采过程中采矿头的动态特性分析具有重要的参考意义。