基于模块度和均衡度的复杂产品架构评价方法
2021-11-16魏云篷陈永亮索树灿
魏云篷,陈永亮,索树灿
(天津大学机械工程系,天津 300354)
通过对一定范围内的不同功能或相似功能的产品进行功能分析,对产品进行分解,建立通用的模块系列,再选用模块来组合出多样化的新产品,以满足市场多样化需求的设计方法称为模块化设计[1]。同样,通过模块化设计产生的模块的组合,可以进一步表达产品架构。产品架构是综合设计理论、软件工程、运作管理和产品开发管理等多学科的知识而形成的,是将产品功能分配给物理组件而形成的系统性方案[2],体现了产品的分解和集成。产品的物理组件及其关系可以用复杂网络表示。复杂网络是现实世界中复杂系统的一种抽象表现形式。现实世界中存在很多类型的复杂网络,例如社交网络、技术网络和神经网络等。Newman[3]于2002年提出了复杂网络的“社团结构”概念。在随后的几年中,复杂网络的研究受到了众多学者的关注[4-5]。
产品模块的划分是模块化设计的关键环节,国内外学者对此进行了大量研究。Tsai等[6]根据零件的几何约束、机械强度、能量和信号建立相关度矩阵,并用制造和装配的信息熵对产品模块的划分结果进行评价。潘双夏等[7]根据产品的客户需求、几何相关性和物理相关性建立相关度矩阵,并用装配、成本、维修的信息熵对产品模块的划分结果进行评价。王日君等[8]根据产品的功能相关性和结构相关性建立相关度矩阵,并用横系列设计复杂度、纵系列设计复杂度和更新换代设计复杂度对模块划分结果进行评价。李中凯等[9]根据产品的功能、结构、寿命、材料和回收的相关性建立相关度矩阵,并用最小描述长度对模块划分结果进行评价。毛保全等[10]提出了用设计制造的复杂度、成本和维修的信息熵对模块划分方案进行评价的方法。吕健等[11]根据产品的功能相关性和结构相关性建立相关度矩阵,并用设计复杂度、装配复杂度、维护复杂度、更新升级复杂度和循环利用复杂度对模块划分结果进行评价。李爱平等[12]根据客户需求相关性矩阵、功能性矩阵、几何相关性矩阵和物理相关性矩阵建立相关度矩阵,并用装配复杂度、客户参与变型设计的复杂度、模块相对独立性和模块内部元素的亲密度对模块划分结果进行评价。Gu等[13]提出了面向产品全生命周期的模块划分方法,根据产品生命周期各阶段的目标要求建立各相关矩阵,并由设计人员对以每个设计目标为基础得出的模块划分方案进行比较,选出最佳方案。田楚楚[14]用模块化程度和模块化效益对模块划分方案进行评价。陈永亮等[15]基于可适应信息熵提出了产品可适应度评价。还有学者用综合评价方法从不同角度对模块划分方案进行了评价[16-18]。
以上研究大多是建立产品不同要素之间的相关度矩阵,并用信息熵等单一指标对模块划分结果进行评价的。而对于复杂产品,由于其零部件众多,以上方法可能不再适用。因此,笔者提出复杂产品的相关度矩阵建立方法和模块划分结果的评价方法。首先,介绍复杂产品相关度矩阵的建立方法;其次,提出复杂产品模块划分方案的综合评价指标;最后,以盾构螺旋输送机为例,利用层次聚类得到不同的模块划分方案,用提出的综合评价指标评价模块划分方案,并从中选出最优方案,以此来得到螺旋输送机的最优产品架构。
1 复杂产品相关度矩阵的建立
研发成本高、生产规模大、技术含量高、单件或小批量定制化、集成度高的大型产品,系统或基础设施称为复杂产品[19]。
1.1 复杂产品的网络图
复杂产品的零件之间存在着约束关系。当产品的零件数n=6时,根据零件之间的关系可以建立复杂产品的网络图,如图1(a)所示,其中存在顶点和边两种元素。设网络图为G,则:
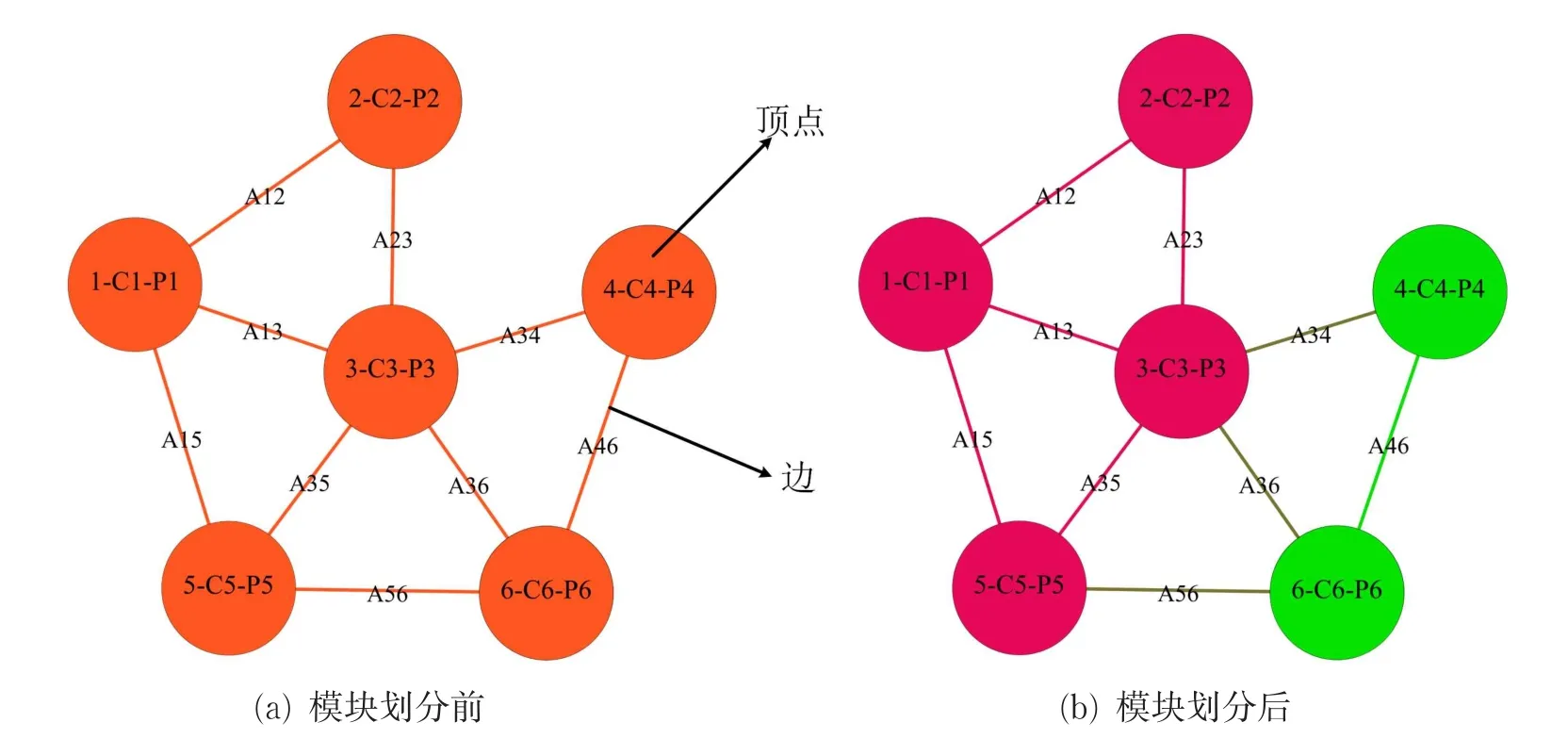
图1 复杂产品网络图Fig.1 Network diagram of complex product

式中:V为顶集,包括组成产品的所有零件;E为边集,包括所有零件之间的关系,即相关度矩阵。
一般地,当产品有n个零件时,则:
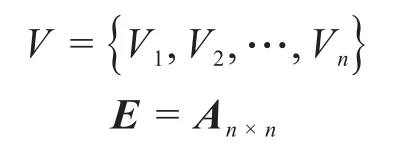
式中:A为产品的相关度矩阵。
同时,零件具有成本、复杂度属性。设零件的属性集为R,则:
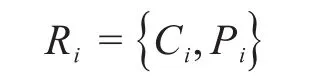
式中:Ri为零件i(i=1,2,…,n)的属性集;Ci为零件i的成本;Pi为零件i的复杂度。
模块划分后的产品网络图如图1(b)所示。共划分为M1和M2两个模块,模块1包含零件1,2,3,5,模块2包含零件4,6,即:
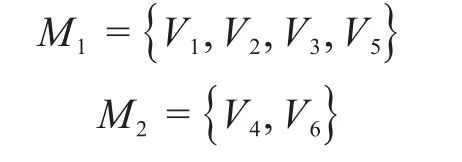
1.2 复杂产品的相关度矩阵
对于复杂产品,因其零件数量众多,直接建立零件间的相关度矩阵比较困难,且大部分已有模块划分方案。因此,根据复杂产品已有的模块划分方案对产品的每个模块建立相关度矩阵。假如产品由n个零件组成,已有划分方案将产品划分为m个模块,则产品最终的相关度矩阵为An×n,每个模块的相关度矩阵(子矩阵)为Ai(i=1,2,…,m)。将所有模块的相关度矩阵构造成分块矩阵,再添加模块间的相关度值即得到整个复杂产品的相关度矩阵。复杂产品相关度矩阵的建立过程如图2所示。

图2 复杂产品相关度矩阵的建立过程Fig.2 Establishment process of complex product correlation matrix
复杂产品零件间的相关度取值见表1。这里考虑的是零部件之间的连接关系。

表1 复杂产品零件间的相关度取值Table 1 Value of correlation between parts of complex product
2 基于层次聚类的模块划分方案的生成
2.1 层次聚类数据的准备
凝聚层次聚类(agglomerative hierarchical clustering,AHC)是一种自下向上聚合数据的聚类算法。根据算得的每一种类别的数据点与所有数据点之间的距离来确定它们之间的相似度,距离越小,则相似度越高。将最为相似的2个数据点进行组合,成为一个新的数据点,并替换掉原来的那2个数据点,再进行下次聚合。
得到相关度矩阵后,须对相关度矩阵进行处理。
首先,将相关度矩阵A转换为距离矩阵D。相关度值越大,两零件间的关系越密切;而对于距离来说,两零件间的距离越小,则其关系越密切。距离矩阵D为:

式中:B为元素全为1的矩阵。
其次,对矩阵D进行标准化处理得到矩阵D'。D'中的元素利用式(2)进行计算。
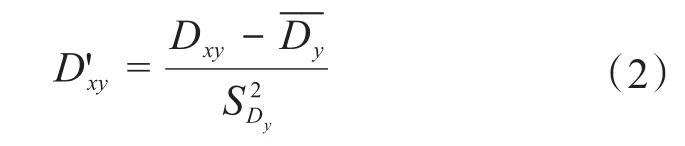
式中:Dxy、D'xy分别为矩阵D和D'第x行、第y列的元素;为矩阵D第y列数值的平均值;为矩阵D第y列数值的方差。
最后,通过矩阵D'计算距离,得到层次聚类所需要的向量T。设duw为向量u(矩阵D'的第u行)和向量w(矩阵D'的第w行)的距离,则:
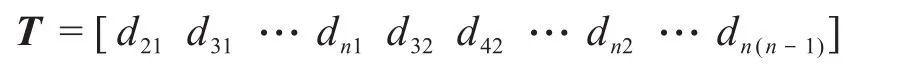
计算距离时可以采用欧几里德距离、马哈拉诺比斯距离、曼哈顿距离、相关距离和夹角余弦距离等,这里采用相关距离进行计算,即:
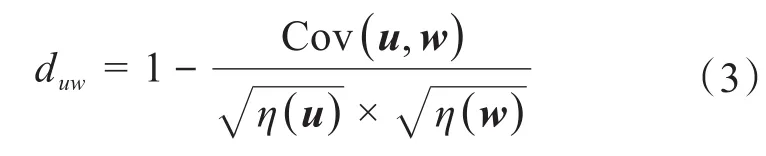
式中:Cov(u,w)为向量u和向量w的协方差;η(u)、η(w)分别为向量u、w的方差。
得到向量T后,利用MATLAB的linkage函数进行聚类。聚类时采用平均距离(average)进行计算。
2.2 模块划分结果的表示
利用层次聚类划分模块后,可得到不同的模块划分方案。则具有n个零件,被划分为m个模块的产品可表示为:{M1,M2,…,Mm}。其中,Mj={Vi}(i=1,2,…n;j=1,2,…,m)。
对于每个模块划分方案,存在以下条件:
1)Mj≠∅,表示每个模块内必须有零件;
2)Mj1∩Mj2=∅(j1≠j2),表示2个模块中不会出现同一零件,即一个零件只属于一个模块;
3 模块划分方案评价指标的建立和计算
3.1 模块度
模块度是衡量模块划分效果的指标之一,最早由Newman提出[20]。模块度越大,表明模块划分效果越好。模块度Q的计算公式如式(4)所示。Q值范围为[-0.5,1),当Q=0.3~0.7时,说明聚类效果较好。
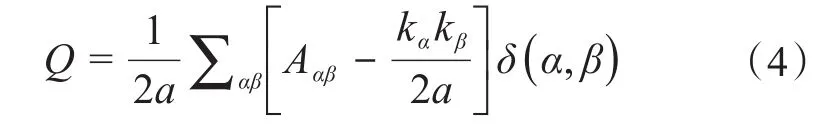
式中:2a为网络中所有顶点的度(即与该顶点相连的边的总数,若边带权重,则为权重之和,;α和β为其中的2个顶点;Aαβ为顶点α与顶点β的相关度;kα、kβ分别为顶点α、β的度;δ(α,β)表示α与β是否在同一个模块,如果α与β在同一个模块,则此值为1,否则为0。
3.2 最小描述长度
最小描述长度由Rissanen提出[21],最初应用于编码。最小描述长度L的计算公式如式(5)所示。其包含2项,第1项为模块之间运动的熵,第2项为模块内运动的熵(其中退出模块也被视为运动)。每一项都是根据它在特定分区中出现的频率来加权的。
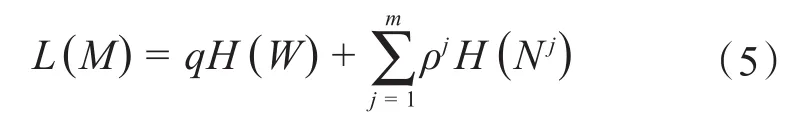
式中:q为随机游走在任何给定步骤中切换模块的概率;H(W)为模块编码的熵;H(Nj)为模块内部运动的熵,包括模块j的退出编码;权重ρj为模块j中发生的模块内运动的概率和退出模块j的概率。
3.3 均衡度
1)成本均衡度。
从成本的角度考虑,产品实际的生产和装配成本与每个模块的成本有很大的关系。在模块划分过程中应尽量使模块的成本均衡,这样能够降低维修和更换零部件的成本,因此提出了成本均衡度。
成本均衡度的计算过程如下:首先根据模块划分方案计算每个模块的成本(即该模块中所有零件的成本。对于结构类零件,可用单位质量的价格乘以零件质量;对于密封类零件,可用单位长度的价格乘以零件长度;对于外购件,则为直接购买的价格)。得到各模块的成本之后,根据式(6)计算成本的信息熵:
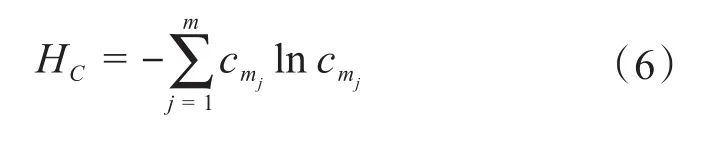
式中:HC为产品成本的信息熵;cmj为模块j的相对成本,为模块j的成本。
成本的信息熵值反映了模块划分的多少及各模块成本分布的均匀程度:模块划分越多,各模块的成本相差越小,熵值就越大。但在不同的模块划分方案下,当模块数不同时,信息熵值缺乏可比性[22]。因此,基于该信息熵函数引入模块划分的成本均衡度公式,在理论上当各模块的成本相等时,信息熵取得最大值HCmax=lnm。因此成本均衡度JC为:

JC取值为0~1,JC值越大,表明各模块的成本越均衡。
2)复杂度均衡度。
制造和装配模块的工作量即为模块的复杂度。在复杂产品的模块划分中,应尽量使模块的复杂度均衡。复杂度的计算公式如式(8)所示,其包含2项:第1项为模块内每个零件的复杂度,与模块制造时的工作量相关联;第2项为模块内各零件由于连接关系产生的额外复杂度,与模块装配时的工作量相关联。
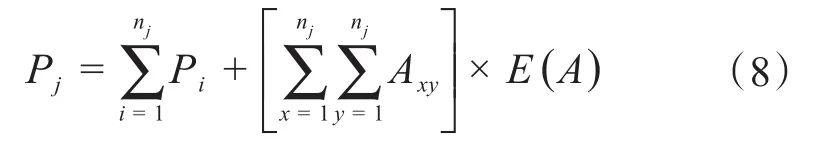
式中:Pj为模块j的复杂度;nj为模块j中零件的个数;Axy为矩阵A中第x行、第y列的元素λb为相关度矩阵A的第b个特征值。
与成本均衡度类似,得到每个模块的复杂度后,再通过式(9)计算复杂度信息熵:
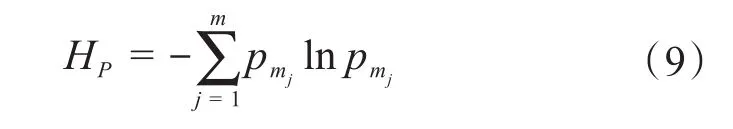
式中:HP为产品复杂度的信息熵;pmj为模块j的相对复杂性为模块j的复杂度。
同理,在不同模块划分方案下,当模块数不同时,信息熵值缺乏可比性。因此,基于该信息熵函数引入模块划分的复杂度均衡度公式,在理论上当各模块的复杂度相等时,信息熵取得最大值HPmax=lnm。因此复杂度均衡度为:

JP取值为0~1,JP值越大,表明各模块的复杂度越均衡。
3.4 评价指标的计算
在计算模块度和均衡度时,须利用X矩阵表示模块划分方案。每一种划分方案对应一个X矩阵,X矩阵中的元素只为0或1。

计算完各个指标后,最终的综合评价指标I为:

式中:f为评价指标个数;ωt为第t个评价指标的权重值;It为第t个评价指标。
模块度和均衡度的计算过程如图3所示。
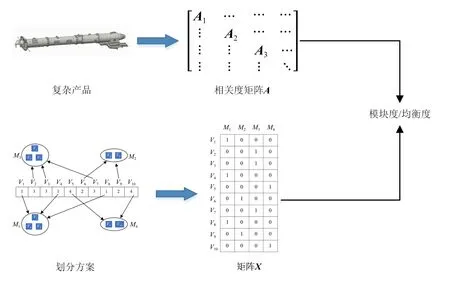
图3 模块度和均衡度的计算过程Fig.3 Calculation process of modularity and equilibrium
4 基于熵权法的评价指标权重的计算
利用熵权法确定模块划分方案评价指标的权重,步骤如下:
1)建立模块划分指标矩阵S,若有g个划分方案、f个评价指标,则S为g×f阶矩阵,srt为第r个划分方案的第t个指标值 (r=1,2,…,g;t=1,2,…,f),S=(srt)g×f。
2)对数据进行标准化处理,将指标绝对值转化为相对值zrt,正向指标zrt+和负向指标zrt-如式(12)所示:
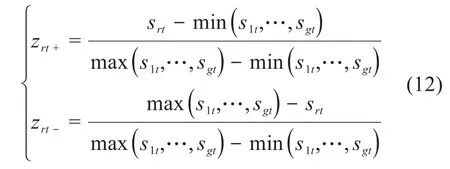
3)根据式(13)计算划分方案中各指标所占的比重εrt,然后根据式(14)计算各个指标的信息熵值et。
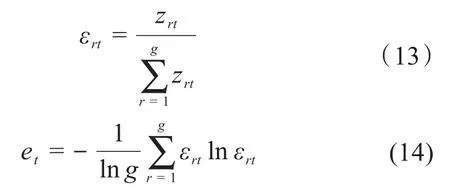
4)根据式(15)计算出划分方案中各项指标的客观权重值ωr。
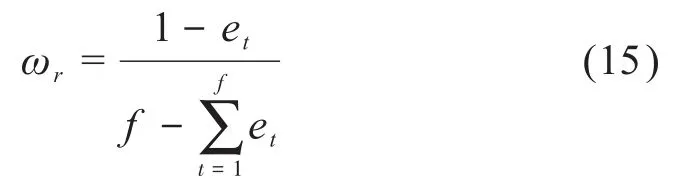
5 案例分析
以盾构螺旋输送机为例来验证所提出的复杂产品架构评价方法的正确性。螺旋输送机是土压平衡盾构机排土和建立土压平衡的主要设备,其结构如图4所示。螺旋输送机工作时,深入土舱内的螺杆和螺旋叶片在液压马达的驱动下旋转,土舱内的土碴随着螺旋轴的旋转而上升,然后经出碴门排出[23]。螺旋输送机的零件数众多,集成度高,研发成本高,属典型的复杂产品。因此,模块划分对其设计、制造、装配和维修具有重要意义。
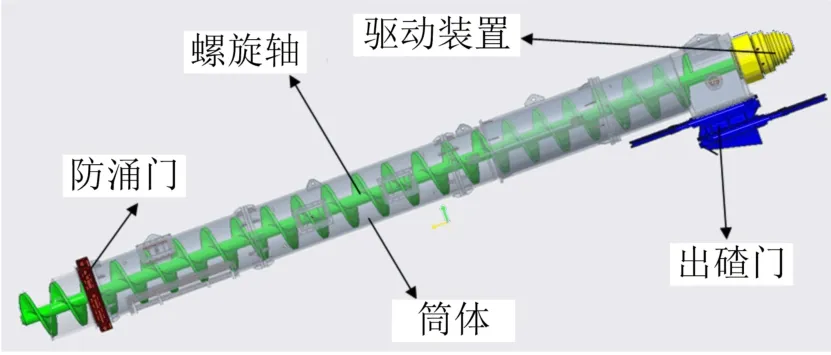
图4 盾构螺旋输送机的结构Fig.4 Structure of shield screw conveyor
5.1 盾构螺旋输送机相关度矩阵的建立
盾构螺旋输送机已有的模块划分方案如表2和图5所示,共分为出碴门、伸缩节、连接节、防涌门、驱动装置和螺旋轴六个模块。
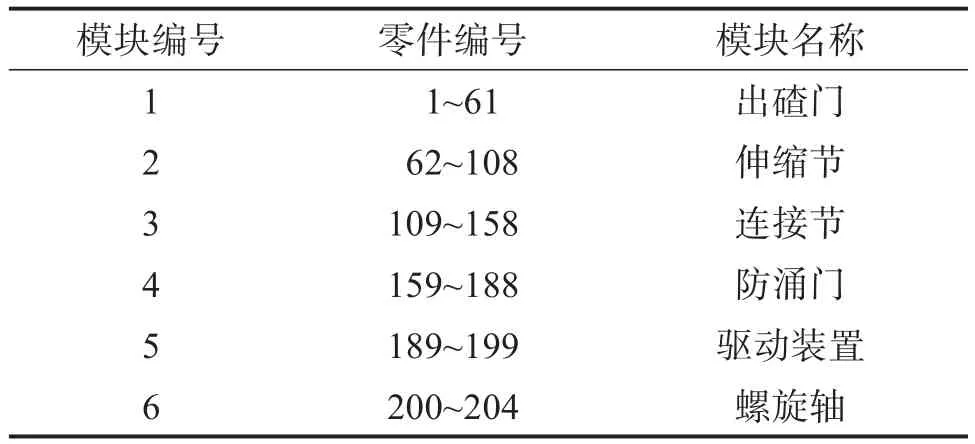
表2 盾构螺旋输送机已有模块划分方案Table 2 Existing module division scheme of shield screw conveyor
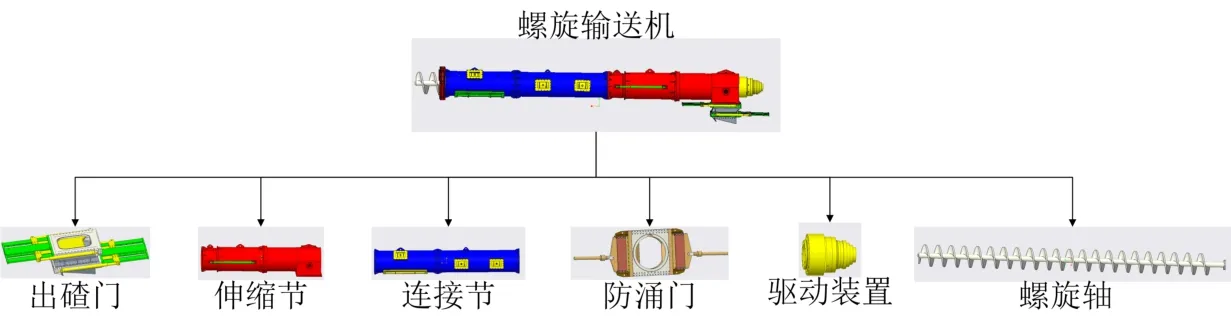
图5 盾构螺旋输送机已划分的模块Fig.5 Existing division modules of shield screw conveyor
利用这6个模块构造螺旋输送机的相关度矩阵。首先建立每个模块的相关度矩阵A1、A2、A3、A4、A5和A6,其网络图如图6所示。图中顶点以“零件编号-成本-复杂度”示出,其中:零件成本通过表3算得;零件复杂度根据零件制造时的难易程度进行量化而得出,如表4所示。
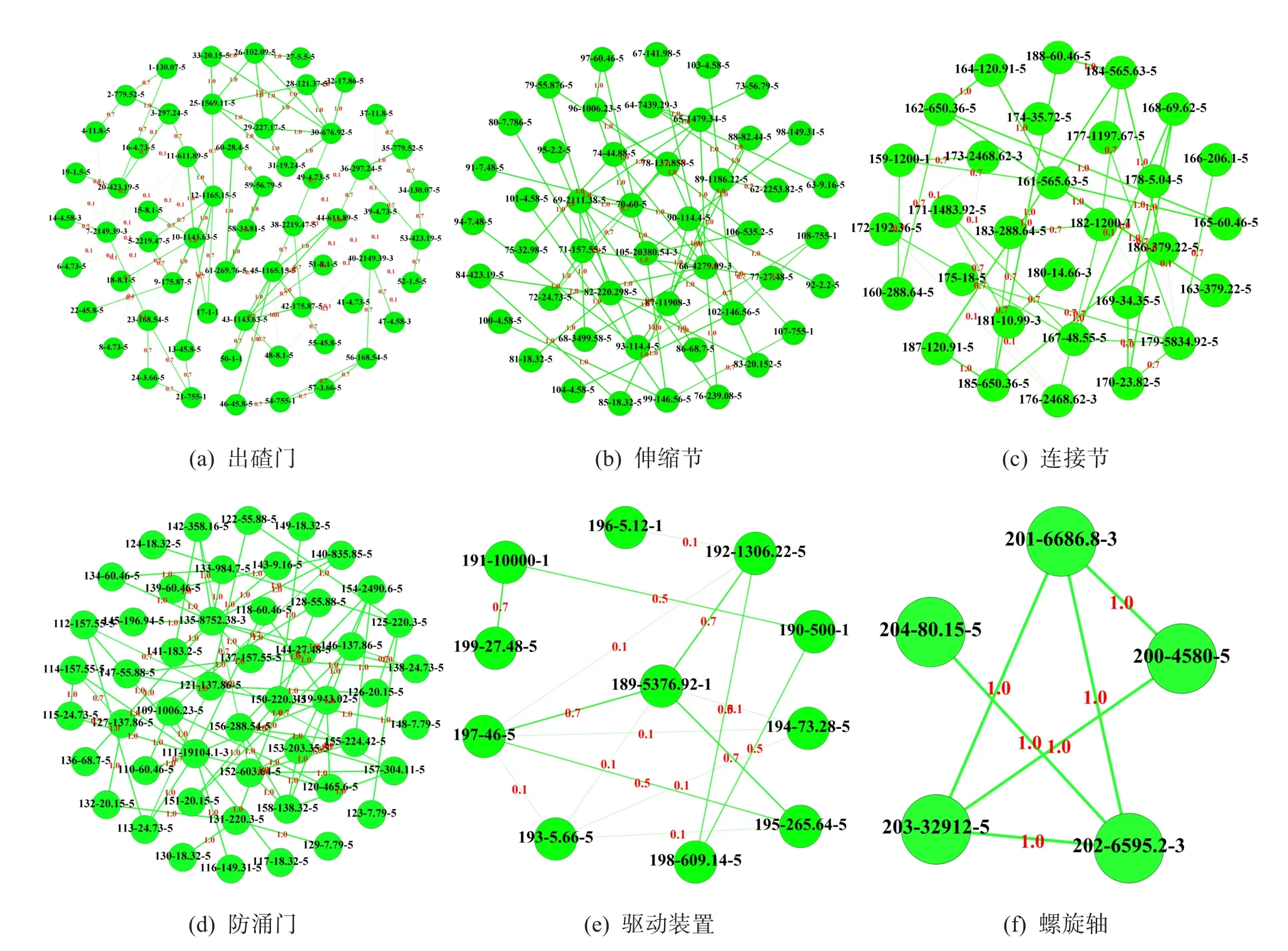
图6 盾构螺旋输送机已有划分模块的网络图Fig.6 Network diagram of existing division modules of shield screw conveyor

表3 盾构螺旋输送机的零件成本Table 3 Parts cost of shield screw conveyor

表4 盾构螺旋输送机的零件复杂度Table 4 Part complexity of shield screw conveyor
6个模块的相关度矩阵建立后,再添加模块间的相关度。这6个模块间的连接均为螺栓连接,相关度为0.7。其连接关系如图7所示。在相关度矩阵中的对应位置添加模块间的相关度数值后,即得到盾构螺旋输送机整体的相关度矩阵A,其整体网络关系如图8所示。
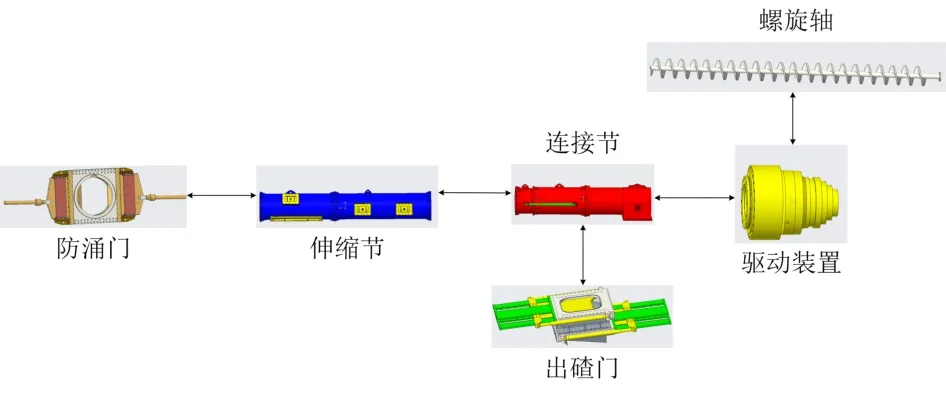
图7 盾构螺旋输送机6个模块间的连接关系示意Fig.7 Schematic of connection relationship between six modules of shield screw conveyor
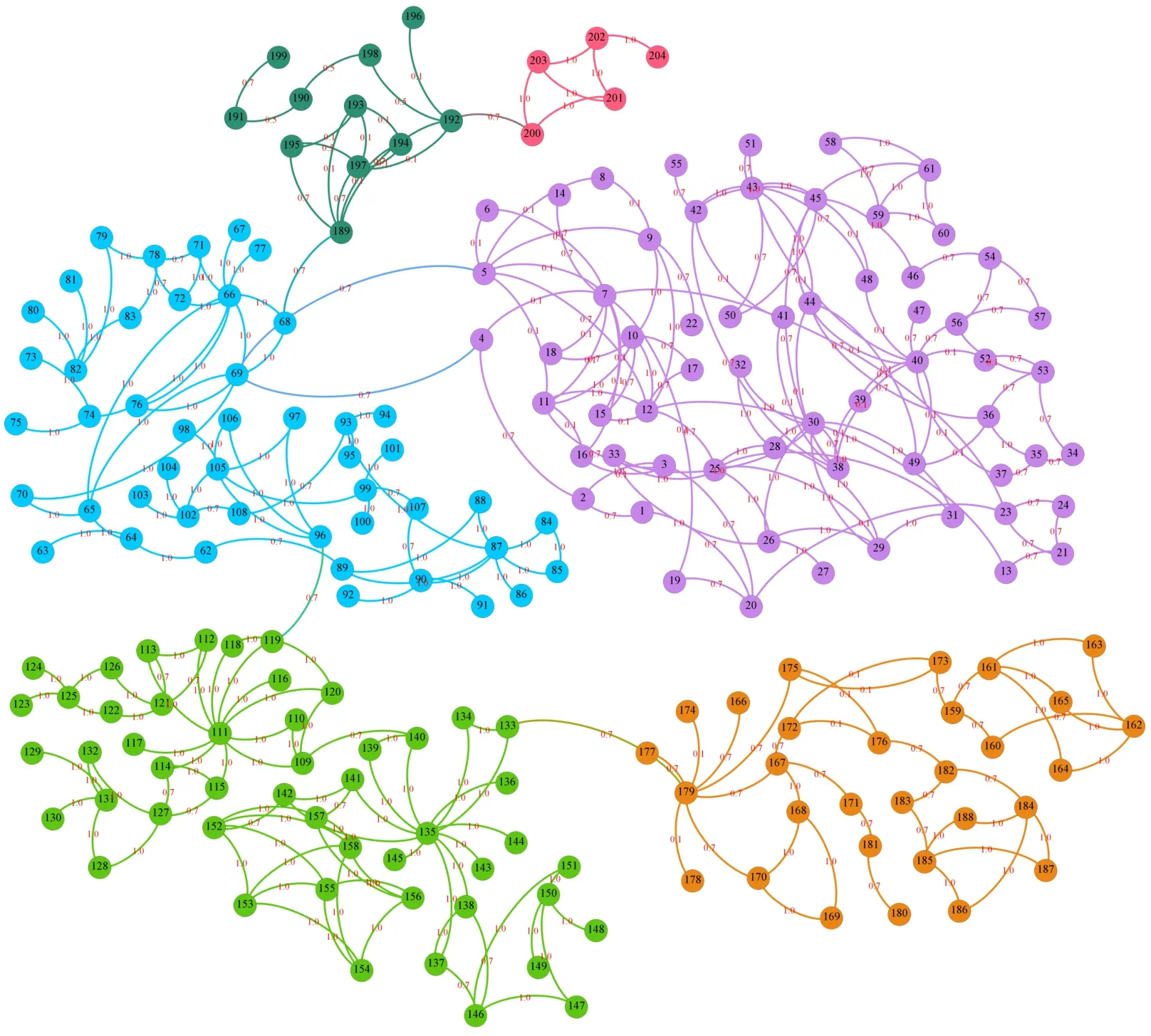
图8 盾构螺旋输送机整体网络图Fig.8 Overall network diagram of shield screw conveyor
5.2 盾构螺旋输送机的模块划分
利用层次聚类进行模块划分。不同的聚类数形成不同的模块划分方案。一般地,产品的模块数不会超过零件数的算数平方根。螺旋输送机共有204个零件,因此取最大模块数为15(> 204≈14.28),得到如表5所示的模块划分方案。
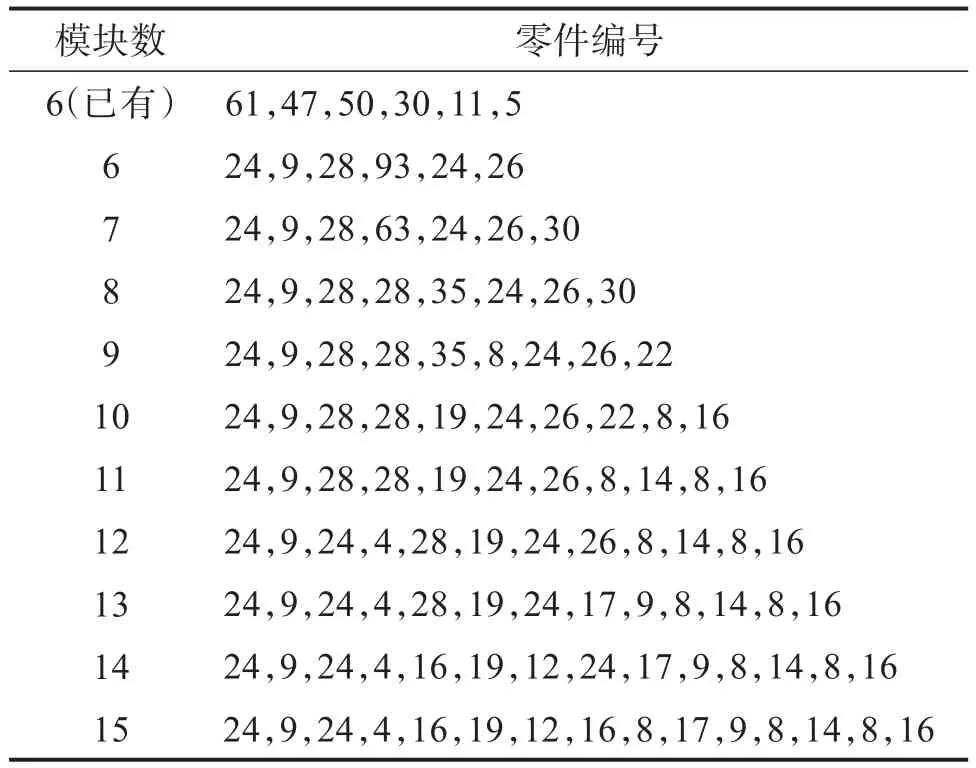
表5 盾构螺旋输送机模块划分方案Table 5 Module division scheme of shield screw conveyor
5.3 盾构螺旋输送机模块划分方案的评价
计算盾构螺旋输送机模块划分方案的评价指标,结果如表6和图9所示。最小描述长度值越小,其他三项指标值越大,则模块划分效果越好,制造和装配效率越高。最小描述长度取值范围不在0~1之间,因此对其取倒数并作归一化处理,得到-L。
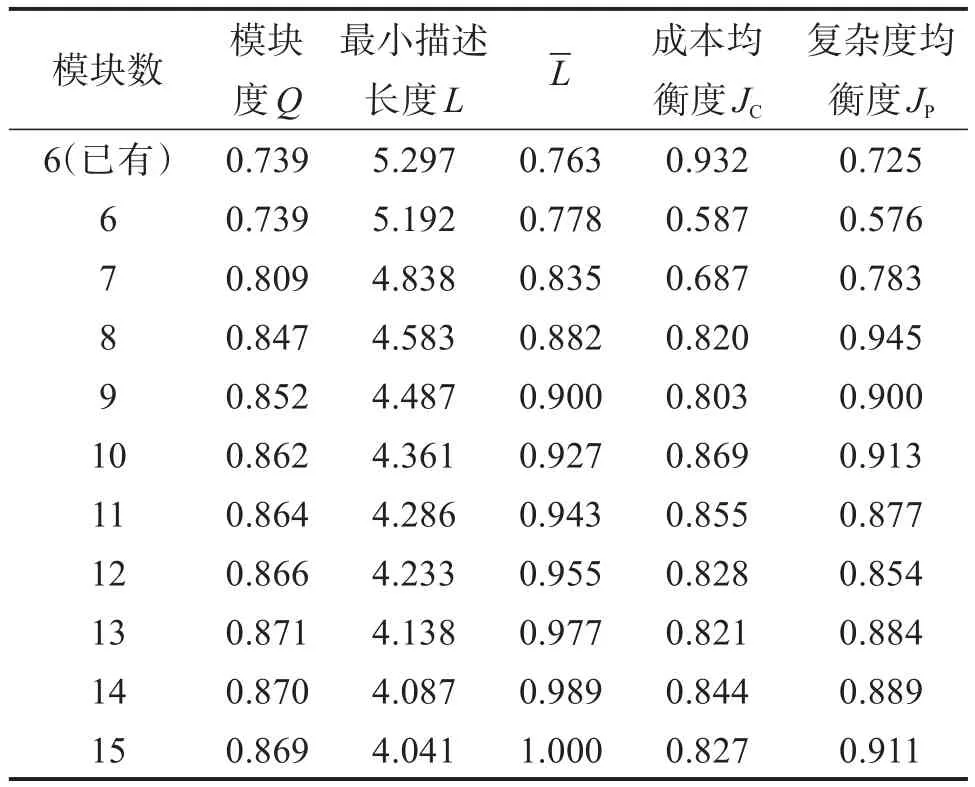
表6 盾构螺旋输送机模块划分方案的评价指标值Table 6 Evaluation index value of module division scheme of shield screw conveyor
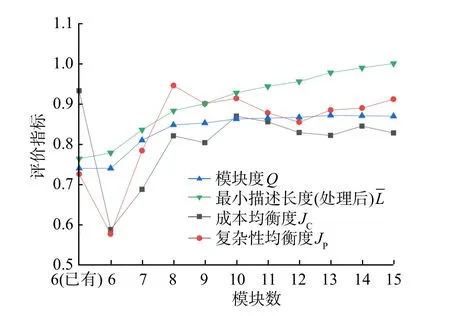
图9 盾构螺旋输送机模块划分方案评价指标的变化曲线Fig.9 Changing curves of evaluation indexes under different module division schemes of shield screw conveyor
由图9可知,模块度与最小描述长度(处理后)的变化趋势类似,成本均衡度与复杂度均衡度的变化趋势类似。经过计算可得,模块度和最小描述长度(处理后)的相关系数为0.94,成本均衡度和复杂度均衡度的相关系数为0.62。
成本均衡度与复杂度均衡度的相关系数比模块度与最小描述长度(处理后)的相关系数小,因此,在选择综合评价指标时,在模块度和最小描述长度中选择一个,成本均衡度、复杂度均衡度则都须考虑。
1)考虑模块度、成本均衡度和复杂度均衡度时,利用熵权法确定其权重值为:
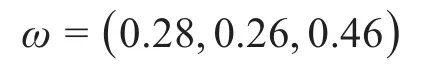
此时各评价指标值和综合评价指标值如表7所示。
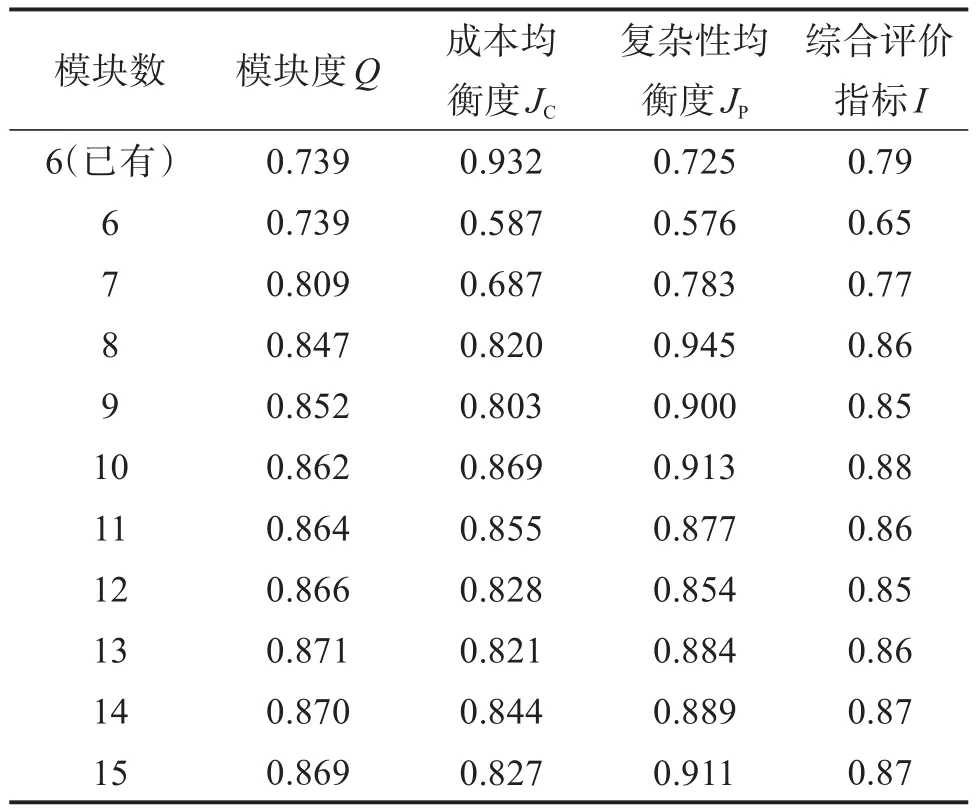
表7 考虑模块度和均衡度时的评价指标值Table 7 Evaluation index value when considering modularity and equilibrium
2)考虑最小描述长度、成本均衡度和复杂度均衡度时,利用熵权法确定其权重值为:

此时各评价指标值和综合评价指标值如表8所示。
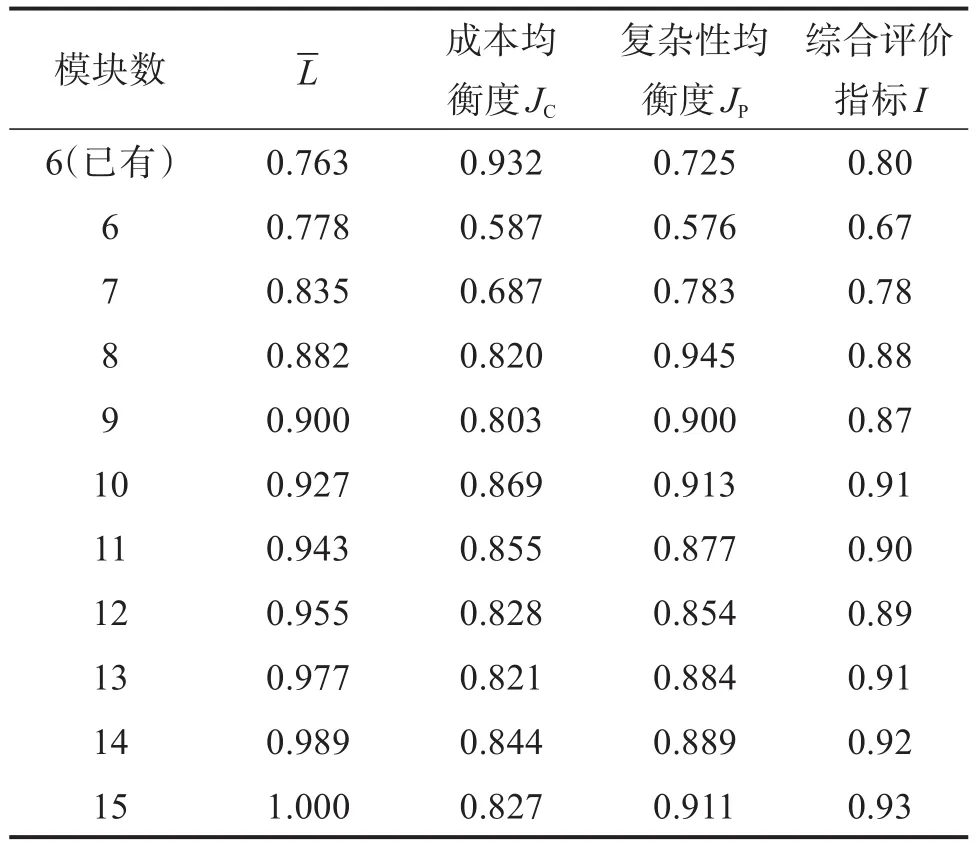
表8 考虑最小描述长度和均衡度时的评价指标值Table 8 Evaluation index value when considering minimum description length and equilibrium
5.4 模块划分方案的改进
2种评价方案下综合评价指标的变化曲线如图10所示。考虑模块度和均衡度时综合评价指标的最大值为0.88,此时模块数为10。考虑最小描述长度和均衡度时综合评价指标的最大值为0.93,此时模块数为15。
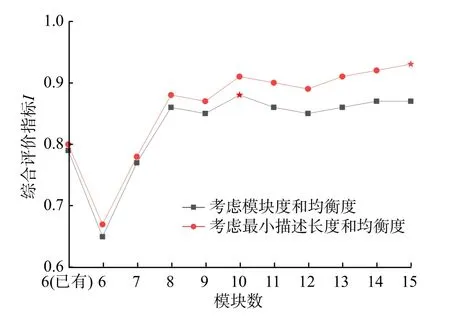
图10 2种评价方案下综合评价指标的变化曲线Fig.10 Changing curves of comprehensive evaluation index under two evaluation schemes
考虑模块度和均衡度时的最优模块划分方案如表9所示,考虑最小描述长度和均衡度时的最优模块划分方案如表10所示。当模块数为15时,伸缩部分分成了两部分(模块6和模块7);将中间节的一个检修门单独分成了一个模块(模块9);将固定节的盖板单独分成了一个模块(模块11);将防涌门分成了左门板、面板、右门板三部分,如图11所示。由于这些部分存在结构和功能上的联系,将其拆开并不合理,因此模块数为10的划分方案较为合理,且其综合评价指标也较好。由于该方案也将防涌门的右门板单独作为一个模块,因此改进方案,将防涌门作为一个模块看待,则为9个模块,如表11所示。
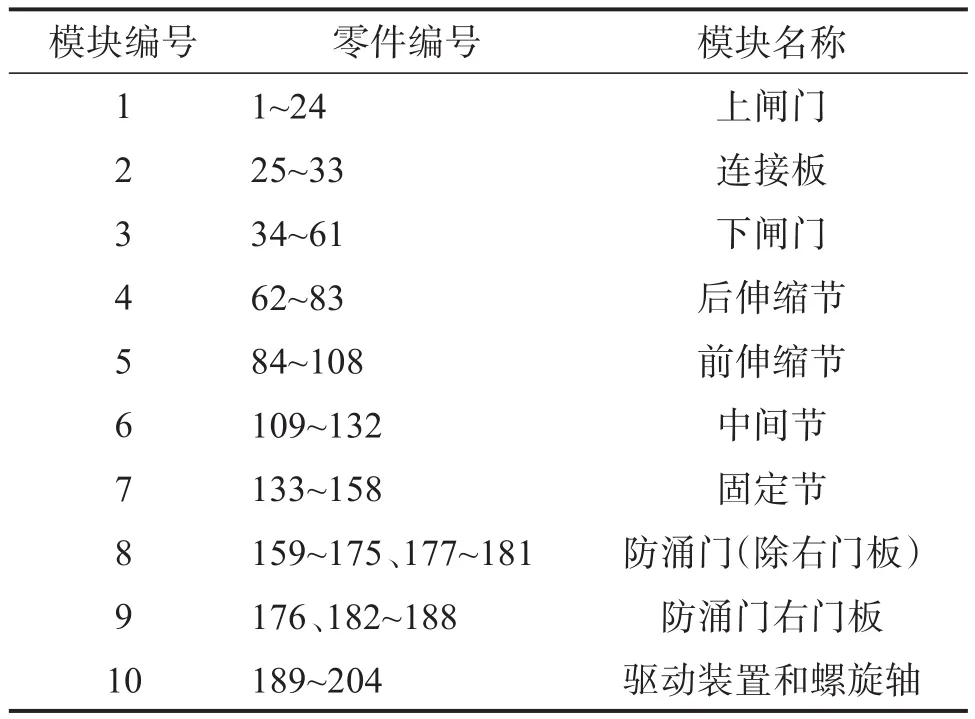
表9 考虑模块度和均衡度时的最优模块划分方案Table 9 Optimal module division scheme when considering modularity and equilibrium

表10 考虑最小描述长度和均衡度时的最优模块划分方案Table 10 Optimal module division scheme when considering minimum description length and equilibrium

图11 考虑最小描述长度和均衡度时最优模块划分方案中的模块6至模块14Fig.11 Module 6 to module 14 in the optimal module division scheme when considering minimum description length and equilibrium
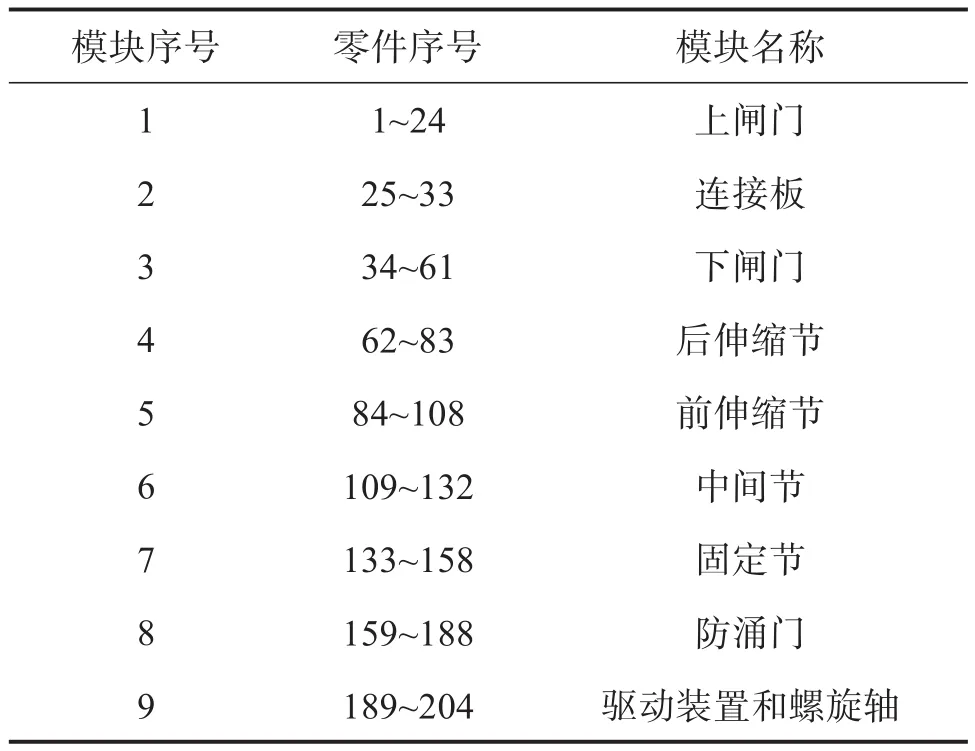
表11 改进后的模块划分方案Table 11 Improved module division scheme
根据改进后的模块划分方案计算模块度和均衡度。虽然模块度由0.862降低到0.855,但是均衡度由1.782提高到1.801,综合评价指标由0.877提高到0.880。不管从评价指标数值还是从实际划分结果来看,改进后的模块划分方案比较合理。方案改进后盾构螺旋输送机的产品架构如图12所示。
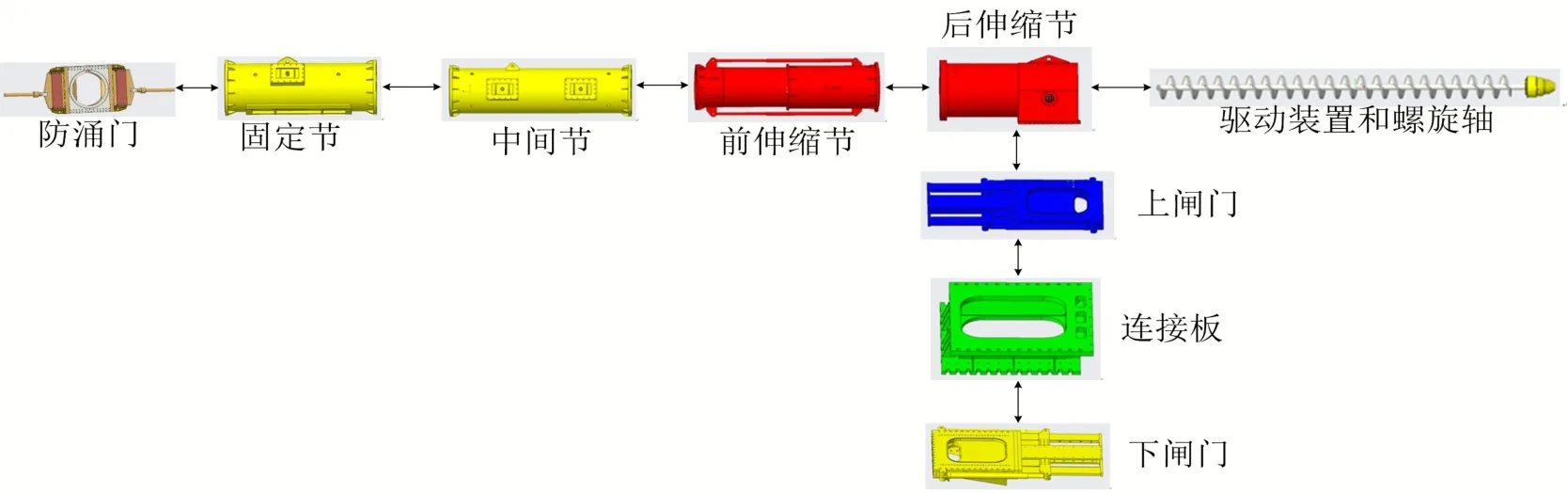
图12 方案改进后盾构螺旋输送机的产品架构Fig.12 Product architecture of shield screw conveyor after scheme improvement
6 结 论
1)提出了复杂产品架构评价方法和评价指标,给出了评价指标的计算公式。结合模块度、最小描述长度建立的复杂产品架构综合评价方法可以解决复杂产品模块划分方案单目标评价时成本与复杂度不均衡的问题,提高了零部件的制造和装配效率。
2)以盾构螺旋输送机为例,对提出的综合评价方法进行了验证,完成了复杂产品架构的评价与改进。结果表明,基于模块度和均衡度的综合评价方法比单目标评价方法合理,可以得到更合理的盾构螺旋输送机产品架构。
