基于指数加权移动平均控制图的沥青路面多变异源施工过程动态控制研究
2021-11-16张宗兵徐志勇杨雄伟
张宗兵,徐志勇,陈 刚,王 云,杨雄伟
(云南建投路面工程有限公司,云南 昆明 650000)
当前沥青路面施工质量过程控制应用较多的是基于控制图的统计过程控制(Statistical Process Control,SPC)研究,其中休哈特控制图中的均值-极差(X-R)控制图是最常用且最基本的控制图类型[1-5],但该类控制图对于均值的波动检测能力不足,且仅考虑样本自身内部的误差来源,缺乏施工过程中多种变异源的分析。国内外大量的研究表明,针对某个变异源的控制纠偏,指数加权移动平均(Exponentially Weighted Moving Average,EWMA)控制图在检测质量参数均值偏移的效果上更加显著,可靠性和实用性也更强[6-7]。但目前针对多变异源的施工过程质量控制缺乏系统的理论分析和应用研究,变异源的指标体系分析匮乏,尚未在路面施工质量管理控制中得到探索实践[8-9],本文对此展开研究。
1 多变异源理论
沥青路面施工过程的多变异源模型如图1所示[9],根据多变异分析理论将沥青路面施工质量特征值分为:原材料内部变异(也称为位置变异,指沥青混合料的质量检测值在不同位置上的变异,如测量沥青混合料的温度时,表面与内部的温度会有差异)、原材料间变异(某个特定批次的沥青混合料,其多个位置上质量检测值的平均值的差异,如同批次沥青混合料每次拌合后相同位置温度的差异)和拌合批次变异(不同批次混合料样本某个指标的质量检测值的差异,如每一批次沥青混合料的温度平均值的差异)三类。
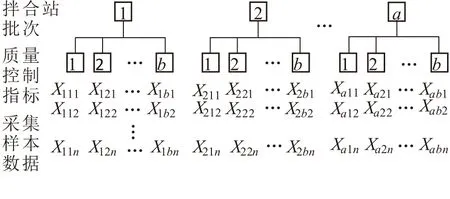
图1 沥青路面施工多变异源过程
在沥青路面施工的多变异源过程中,其质量检测的方差分析方法是区分不同变异源的影响因素,在路面试验段的试验设计阶段求解出各类变异源的影响因子大小。沥青路面施工多变异源过程的数学模型为,它是一种混合式的效应模型(Mixed Effect Model),即包含了随机因素和固定因素。
Xijk=μ+αi+βj(i)+ek(ij)i=1,2,……a;
j=1,2,……b;k=1,2,……n
(1)
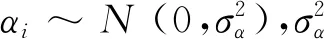
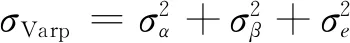
(2)
沥青混合料施工多变异源过程模型的方差分析如表1所示[9]。

表1 多变异源过程方差分析
根据表1的各类样本方差分析,可得到施工各类变异源的方差估计点值为:
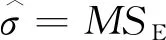
(3)
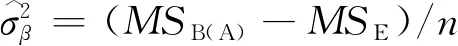
(4)
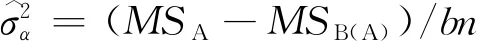
(5)
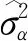
2 多源变异过程的EWMA控制图
指数加权移动EWMA是在移动平均(Moving Average)的控制基础上发展形成的,假设一般情况下检测质量指标的样本数据Xt服从正态分布N(μ,σ2)。则指数加权移动的模型公式为[9]:
Zi=λxi+(1-λ)Zi-1
(6)
式中:λ(0<λ≤1)为常量;Zi为i时刻的指数加权平均值,Zi-1则为上一时刻的指数加权平均值;xi为当前时刻的样本数据检测值,进一步推导公式(6)可得到:
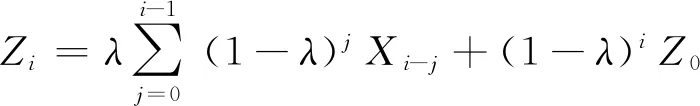
(7)
当i逐渐增大时,Zi的方差为:
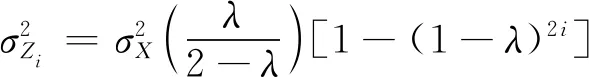
(8)
当i增加到很大时,上式则变为:

(9)
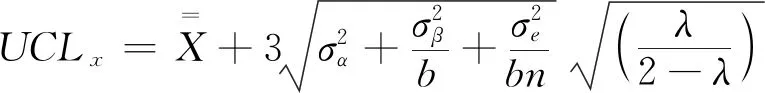
(10)
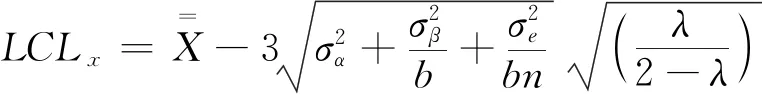
(11)
3 工程应用分析
本文以云南省大嘎高速公路路面施工过程中的沥青混合料温度和沥青质量施工指标为例,详细说明统计过程分析与指数加权移动平均控制图在高速公路施工中的应用。对于拌合站的沥青混合料温度、沥青重量两项指标,选取3个批次的样本,每批抽取8份并在左中右三个位置测量其温度、旋转不同的方向测量重量,即a=3、b=3、n=8,结果如表2、表3所示。
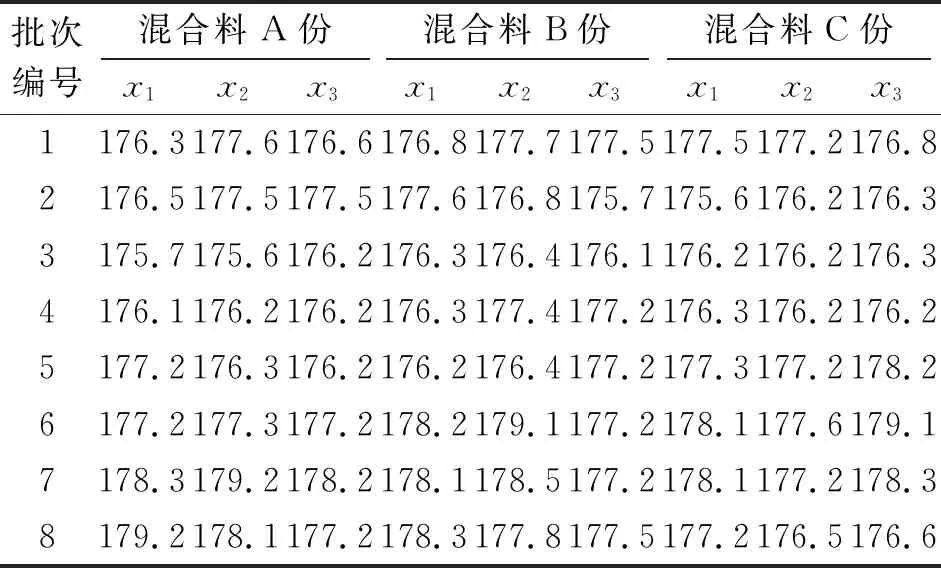
表2 沥青混合料温度观测记录数据 ℃

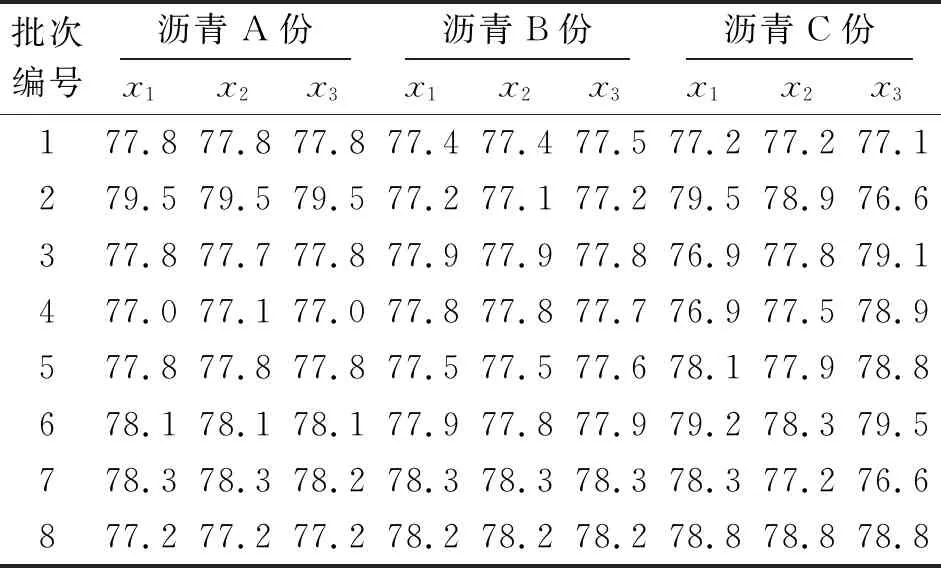
表3 沥青重量观测记录数据 kg
此外,在评价控制图的监控性能时,人们通常采用平均产品长度(Average Production Length,APL)作为度量标准,表4中设置不同的偏移量值以及参数λ,并采用马尔可夫链(MC)方法计算APL值,比较本研究中EWMA和休哈特控制图的APL。结果表明,当不存在偏移时,两者的APL值相等;但当存在偏移(偏移量>0)时,EWMA控制图的APL值显著低于后者(偏移越小越明显),说明EWMA控制图的检测效率更高。

表4 指数加权移动平均控制图和休哈特控制图的检出力及APL对比结果
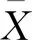
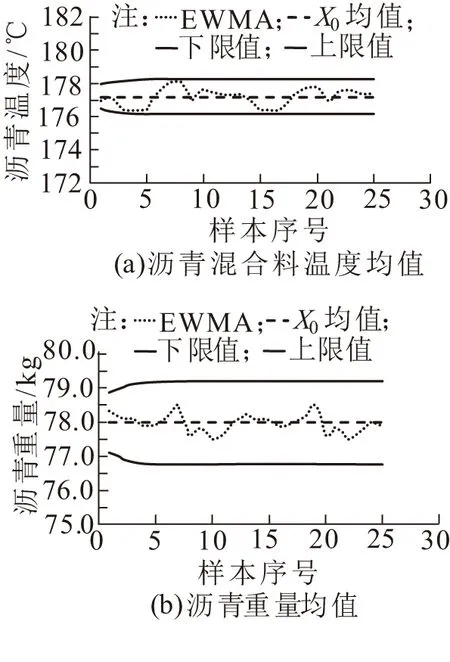
图2 沥青路面施工过程EWMA控制图
由图2可以看出,EWMA控制图上的点包含了前面数据的历史信息,且以更好的APL值对较小的偏移过程进行侦测,此时利用传统的休哈特控制图则无法检测出均值的波动情况。
4 结论
本研究基于多变异源数学模型和统计过程控制分析理论,以高速公路路面施工沥青混合料的指标分析结果为依据,对比分析了常见的质量控制图的适用范围、运行长度、检测能力等特性。在大嘎高速公路路面施工中选取沥青混合料温度和沥青重量指标进行样本数据采集与实践分析,结果表明对于一般的常规休哈特控制图未考虑分析多变异源的影响因素,在多变异源的因素影响条件下,随着均值偏移量的增加,EWMA控制图的检出力比休哈特控制图更高。
