具有空变系数的混合抛物系统在非线性边界条件下解的爆破现象
2021-11-16欧阳柏平肖胜中
欧阳柏平,肖胜中
(1.广州华商学院数据科学学院,广东 广州 511300;2.广东农工商职业技术学院科研处,广东 广州 510507)
抛物方程和抛物系统解的爆破现象的研究在近几十年间取得了丰硕的成果.最初,学者们考虑的是基于三维空间中的齐次边界条件(Dirichlet条件和Neumann条件)和Robin条件下解的爆破问题[1-6],讨论了一定条件下解的全局性、解的爆破率、解的爆破时间的上下界等.之后,有学者进一步考虑了在高维空间中齐次边界条件下以及非线性边界条件下解的存在性、解的爆破时间的上下界等问题[7-12].随着研究的深入,目前有学者又考虑了带有时变或空变系数的抛物方程和抛物系统解的爆破问题研究[13-15],得到了相关的结论.Chen[16-18]等考虑了其他偏微分方程解的爆破问题.近来在实际应用中,发现非局部项的数学模型比局部项的数学模型更有价值.对于非局部项的数学模型来说,需要重新探索解决其数学模型的理论和方法.因为局部项的数学模型的理论和数学方法不再适用.因此,此项课题的研究是非常具有挑战性的,同时也是很有意义的.文献[19-20]研究了Robin边界条件和齐次Dirichlet边界条件下非局部项的抛物方程和抛物系统解的爆破问题.对于解的爆破时间上下界的估计的研究中,考虑和讨论爆破时间上界的方法较多,而对于爆破时间下界的确定则比较困难且办法有限.
文献[20]研究了如下反应-扩散问题
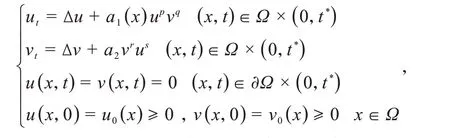
得到了在2种测度下解的爆破时间的下界.受文献[20]的启发,研究如下具有空变系数的混合抛物系统在非线性边界条件下的解的爆破时间的下界

其中,Ω是高维空间R n(n≥3)中的一个有界凸区域,∇代表梯度算子,Δ代表拉普拉斯算子.∂Ω是区域Ω的边界,t*代表可能的爆破时间.分别是u,v在边界∂Ω上的外法向量导数,假设其足够光滑.
同时假设如下条件满足

目前,尚未发现有文献研究具有空变系数的混合抛物系统在非线性边界条件下解的爆破时间的下界估计,其主要困难在于在高维空间上非线性边界条件下找到空变系数对爆破问题的影响.笔者运用高维空间中的Sobolev嵌入不等式以及相关的微分不等式技巧得出非线性条件下爆破发生时解的爆破时间下界估计.
1 爆破时间的下界
需要用到如下Sobolev不等式[21]

其中,C=C(n,Ω)是一个与n和Ω有关的Sobolev嵌入常数.
首先定义辅助函数
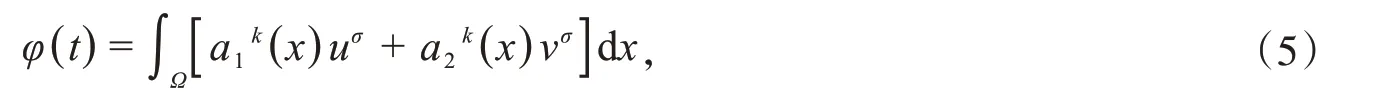
定理1假设u(x,t),v(x,t)是问题(1)~(2)在有界凸区域Ω的经典的非负解,则式(5)中定义的能量满足微分不等式

由此可得爆破时间t*的下界为

其中,R1,R2,R3,R4,R5,R6,ξ1,ξ2,ξ3,ξ4将在下文定义.
2 定理1的证明
为了证明上面的定理,先证明引理1.
引理1 假设u(x,t),v(x,t)是问题(1)~(2)在有界凸区域Ω的经典的非负解,则式(5)中定义的能量满足

证明运用散度定理,首先对式(5)求导数并注意到式(2),得
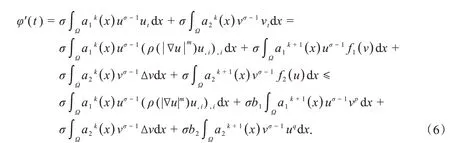
对于式(6)第一项,由散度定理和式(2),有
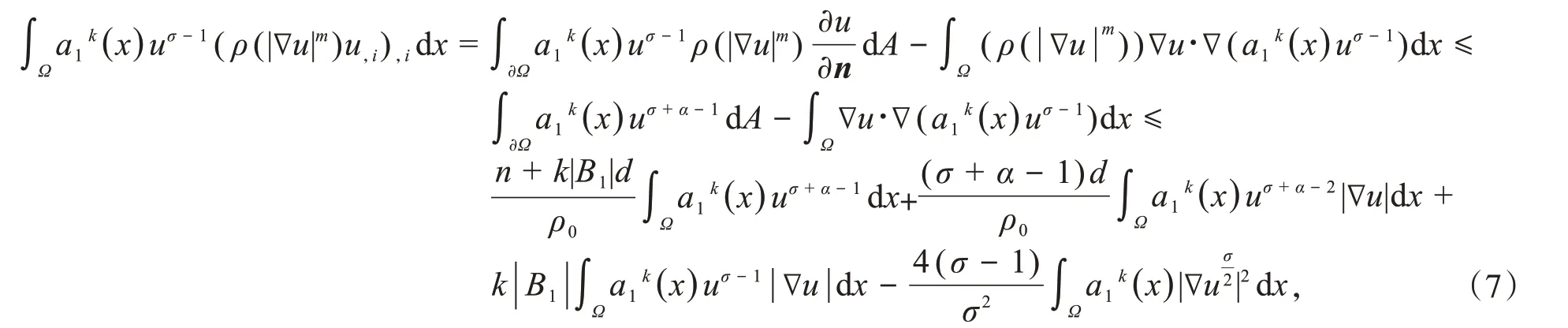
对于式(7)第三项,应用Hölder不等式和Young不等式,得
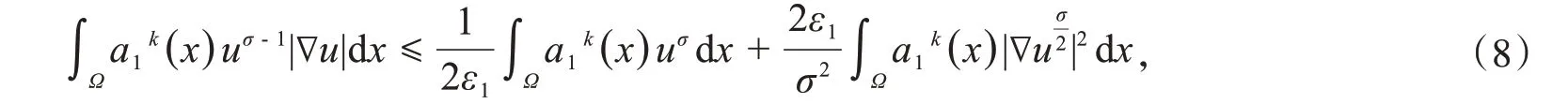
其中,ε1在下文会定义的正数.
对于式(7)第二项,由Hölder不等式和Young不等式,得
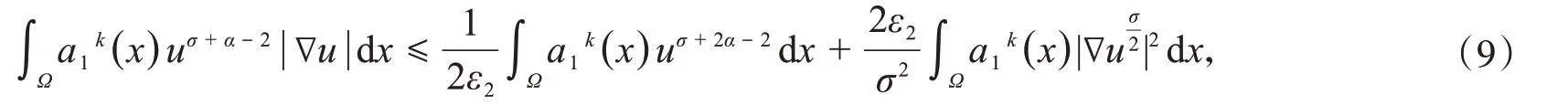
其中,ε2在后面会定义的正数.
又由Hölder不等式,可得
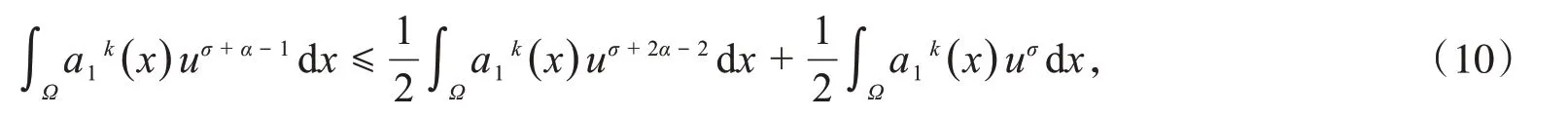
联立式(7)~(10),得

联立式(11)和(12),有

同理,对于式(6)第三项,由散度定理和式(2),有
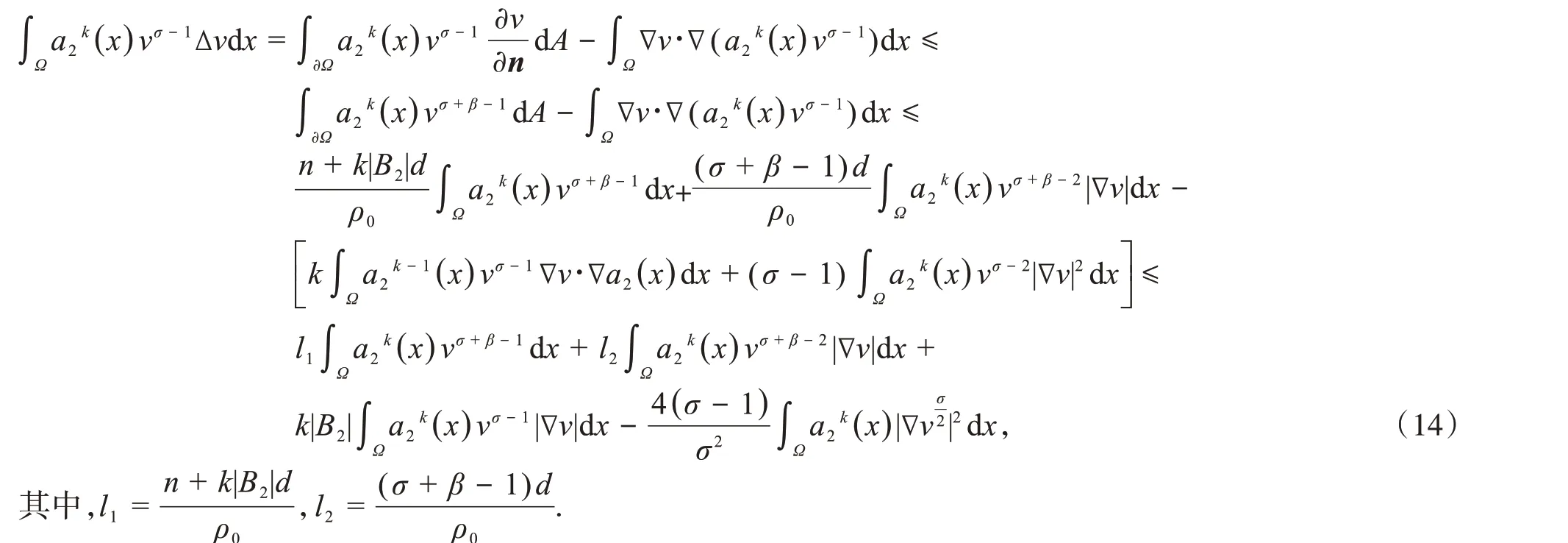
对于式(14)第一项,由Hölder不等式和Young不等式,可得

对于式(14)第二项,应用Hölder不等式和Young不等式,得
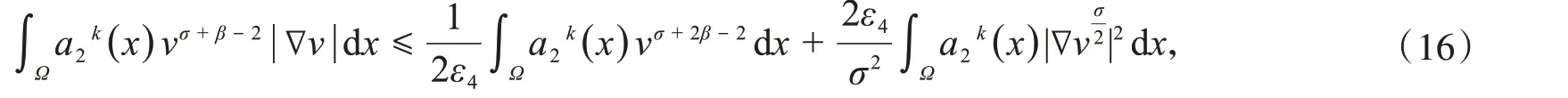
其中,ε4在后面会定义的正数.
对于式(14)第三项,由Hölder不等式和杨氏不等式,有

其中,ε5在下文会定义的正数.
联立式(14)~(17),得


联立式(18)和(19),有

对于式(6)第三项,由Hölder不等式,得


对式(22)第二项,由Hölder不等式,有
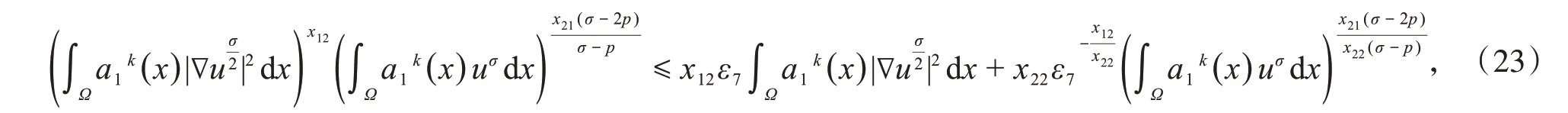
其中,x22=1-x12,ε7在下文会定义的正数.
联立式(21),(22)和(23),可得


同样地,对于式(6)第四项,由Hölder不等式和式(4)以及类似于式(21)的推导,可得
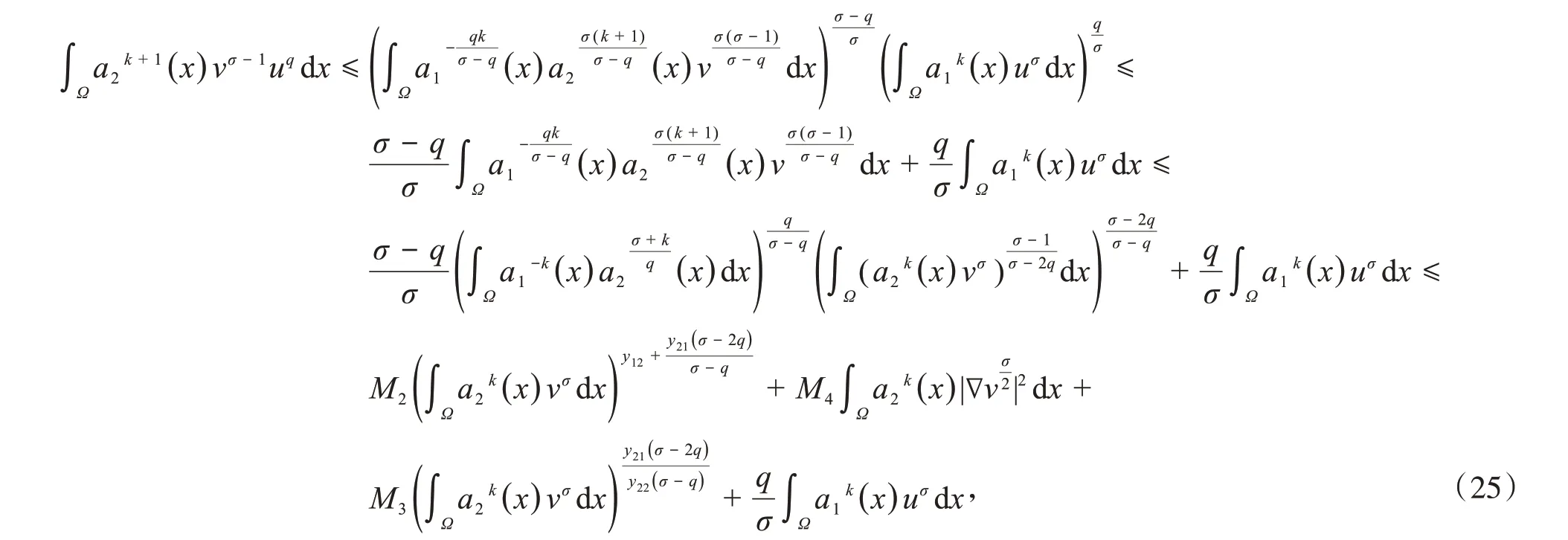
联立式(6),(13),(20),(24)和(25),可得到
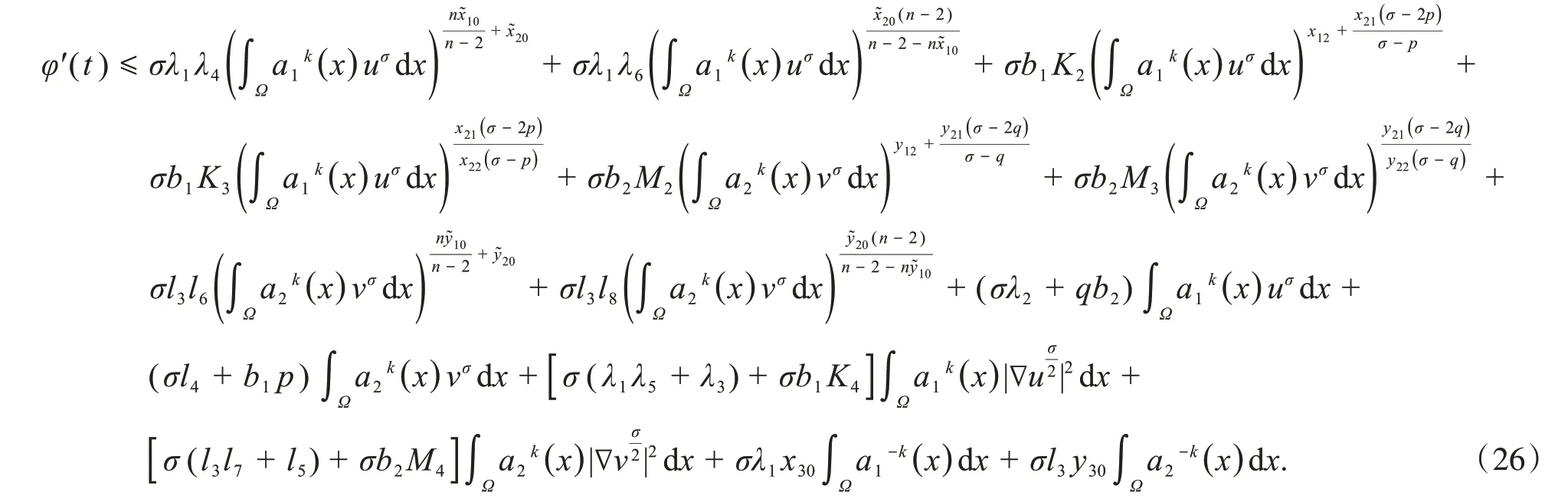
选取合适的ε1,ε2,ε4,ε5,ε7,ε8,使得σ(λ1λ5+λ3)+σb1K4≤0,σ(l3l7+l5)+σb2M4≤0.于是,式(26)化为

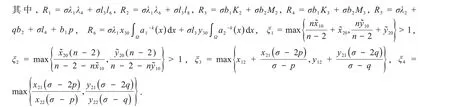
式(27)可写为以下形式
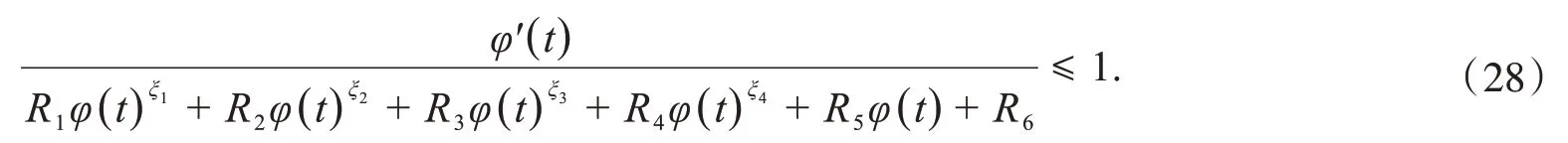
引理1得证.
由引理1,对式(28)积分可得
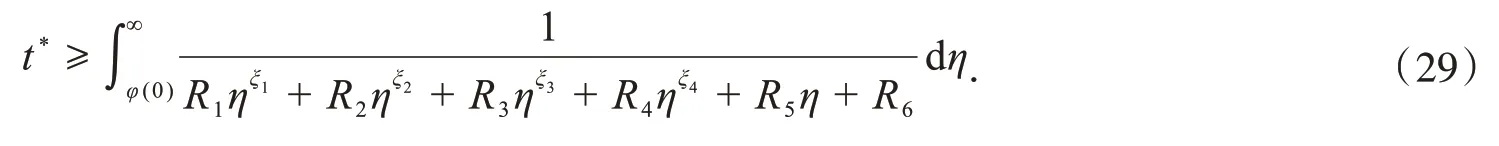
从而,定理1得证.
