巧用口诀助分部积分法的课堂教学*

张 萍

(湖南邵阳学院理学院 湖南 邵阳 422004)

1.问题的引入和公式的推导

答：不正确，引出分部积分公式。

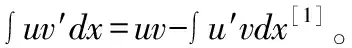
2.口诀的使用

在高等数学中我们所讨论的函数绝大多数都是初等函数，而初等函数指的是由常数、幂函数、指数函数、对数函数、三角函数、反三角函数经过有限次四则运算和复合运算得到，并且能用一个式子表示的函数[1]。为了记忆的方便，我们记幂函数为“幂”，指数函数为“指”、对数函数为“对”，三角函数为“三”、反三角函数为“反”。

如果不定积分的被积函数是两类函数乘积的情形，我们就可以巧用口诀“留下按何序，对反幂指三”来快速求解不定积分。即被积函数的两类函数按照“对反幂指三”的次序，越排在前面的函数类型留下来的优先级越高，留下来不变作为，将剩下的函数写成导数的形式，再使用分部积分公式。

3.应用举例

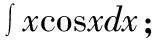
解：被积函数为幂函数x和三角函数cosx乘积的情形，巧用口诀“留下按何序，对反幂指三”。因为幂函数在前，三角函数在后：幂函数x留下不变，将剩下的三角函数cosx写成导数(sinx)′的形式，再使用分部积分公式

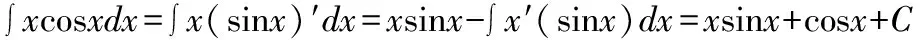
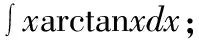
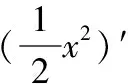
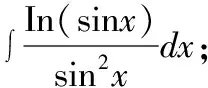
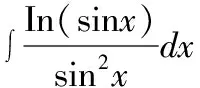
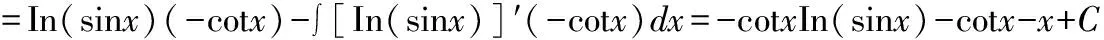
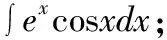
解：被积函数为指数函数ex和三角函数cosx乘积的情形，巧用口诀“留下按何序，对反幂指三”。因为指数函数在前，三角函数在后：选择将指数函数ex留下不变，将剩下的三角函数cosx写成导数(sinx)′的形式，再使用分部积分公式

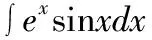
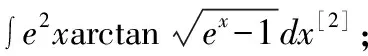
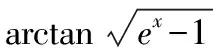
4.结束语

对于初学者，本文提出了巧用口诀“留下按何序，对反幂指三”结合典型例题由浅入深，循序渐进，化繁为简来帮助学生快速地使用分部积分公式，在课堂教学中取得了良好的效果。