一种高效的CD-CAT在线标定新方法：基于熵的信息增益与EM视角*

谭青蓉 汪大勋 罗 芬 蔡 艳 涂冬波

一种高效的CD-CAT在线标定新方法：基于熵的信息增益与EM视角

谭青蓉 汪大勋 罗 芬 蔡 艳 涂冬波

(江西师范大学心理学院, 南昌 330022)

项目增补(Item Replenishing)对认知诊断计算机自适应测验(CD-CAT)题库的维护有着至关重要的作用, 而在线标定是一种重要的项目增补方式。基于数据挖掘中特征选择(Feature Selection)的思路, 提出一种高效的基于熵的信息增益的在线标定方法(记为IGEOCM), 该方法利用被试在新旧题上的作答联合估计新题的矩阵和项目参数。研究采用Monte Carlo模拟实验验证所开发新方法的效果, 并同时与已有的在线标定方法SIE、SIE-R-BIC和RMSEA-N进行比较。结果表明：新开发的IGEOCM在各实验条件下均具有较好的项目标定精度和项目估计效率, 且整体上优于已有的SIE等方法; 同时, IGEOCM标定新题所需的时间低于SIE等方法。总之, 研究为CD-CAT题库中项目的增补提供了一种更为高效、准确的方法。

认知诊断计算机自适应测验, 项目增补, 在线标定,矩阵, 熵的信息增益

1 引言

测评技术与计算机技术的持续发展, 使得大众不仅追求测验的效率, 更追求综合性的测验结果, 而不仅仅是笼统的测验总分。人们渴望获取详实且全面的测验结果, 使其能根据该结果对自身在所测内容领域上的强弱进行系统评估, 了解其需改进或完善的地方, 从而制定进一步的学习计划。认知诊断计算机自适应测验(Cognitive Diagnostic Computerized Adaptive Testing, CD-CAT)是认知诊断(Cognitive Diagnosis, CD)与计算机自适应测验(Computerized Adaptive Testing, CAT)相结合的产物, 其在提高测验效率和准确性的同时, 可为被试提供在所测内容领域上优缺点的详细诊断(Wang, 2013; Weiss, 1982)。因此, 可根据被试的诊断结果对其薄弱知识点进行针对性地教学补救, 较好地满足了当今大众对于高效且周密的测验的需求, 有着广泛的应用前景(Leighton et al., 2004; Liu et al., 2013)。

CD-CAT使用的前提是已建构好的题库。但是题库中的部分题目会随时间的流逝过度曝光或变得过时, 这时需使用新题对这些题目进行替换或者增补(Chen, 2017)。具体来说, 需邀请有经验的领域专家和心理测量学家根据诊断目的编制新题, 然后估计新题的参数, 并将其与题库中的旧题置于同一量尺之上。在线标定技术是传统CAT中一种有效的项目增补方法, 它是指在测验过程中, 让被试同时作答新题与旧题, 然后根据其作答标定新题参数的过程, 且施测者需告知被试他们作答的部分项目将不用于最终能力的评估(陈平, 辛涛, 2011a)。相比于传统的项目增补方法, 在线标定技术的优点在于：(1)无需复杂的事后等值技术便可将新旧题的参数置于同一量尺之上(Chen & Wang, 2015); (2)无需外部标定研究便能在估计被试能力的同时标定新题的参数, 可节省大量人力和物力; (3)相同的测量模式使得被试在作答新旧题时具有相同的动机(Chen et al., 2012)。迄今为止, 在单维计算机自适应测验(Unidimensional Computerized Adaptive Testing, UCAT)和多维计算机自适应测验(Multidimensional Computerized Adaptive Testing, MCAT)领域, 研究者已推荐了多种高效的在线标定方法(Chen, 2017)。在UCAT中, Stocking (1988)提出方法A (Method A)和方法B (Method B), Wainer和Mislevy (1990)推荐一个EM循环的边际极大似然估计方法(OEM), 随后Ban等人(2001)提出多个EM循环的边际极大似然估计方法(MEM)以及BILOG/先验方法(BILOG/ Prior method)。此外, 为克服Method A方法将估计能力值当做被试能力真值的理论缺陷, 陈平(2016)提出了FFMLE-Method A和ECSE-Method A方法。在MCAT中, Chen等人(2017)对Method A, OEM和MEM方法进行拓展, 称其为M-Method A, M-OEM和M-MEM。且在M-OEM和M-MEM方法的基础上推荐M-OEM-BME和M-MEM-BME方法以用于MCAT中项目参数的标定(Chen, 2017)。

然而, 目前CD-CAT中关于在线标定方法的研究较少, 主要包含了两大类。第一类方法主要有Chen等人(2012)提出的CD-Method A, CD-OEM与CD-MEM方法, 其基于Method A, OEM与MEM提出。这类方法在标定新题时, 假设新题的矩阵已知, 仅标定新题的项目参数。事实上,矩阵作为认知诊断的核心成分, 在多数情况下都是未知的。实际中,矩阵多由内容领域专家和测量学专家共同界定, 需耗费大量的人力和物力, 且由专家界定的矩阵容易受到主观因素的影响而造成界定错误。而矩阵的错误界定最终会影响项目参数的估计精度与被试的分类正确性(de la Torre & Chiu, 2016; Rupp & Templin, 2008)。因此, 第二类在线标定方法应运而生, 其同时标定新题的矩阵与项目参数, 以期减少项目标定所耗费的人力物力, 提高项目标定效率。陈平和辛涛(2011b)提出的联合估计算法(Joint Estimation Algorithm, JEA), Chen等人(2015)提出的SIE (Single-Item Estimation)方法以及谭青蓉(2019)提出的SIE-R-BIC和RMSEA-N等方法均属于该类方法。JEA方法借鉴项目反应理论(Item Response Theory, IRT)中被试参数与项目参数的联合极大似然估计(Joint Maximum Likelihood Estimation, JMLE)思路, 将CD-CAT中被试的属性掌握模式估计值视为被试属性掌握模式真值, 然后基于被试属性掌握模式估计值以及被试在新题上的作答使用极大似然估计(Maximum Likelihood Estimation, MLE)的方法来联合估计新题的矩阵和项目参数。不同于JEA方法, SIE使用属性掌握模式的后验分布来代替属性掌握模式估计值, 计算每一个被试的后验预测分布, 然后使用MLE来估计新题的矩阵。与此同时, SIE方法中运用EM算法来估计新题的项目参数。SIE-R-BIC方法是在SIE方法的基础上提出, 其标定新题时充分利用了题库中已有项目的信息, 而RMSEA-N方法通过评估观察作答分布与期望作答分布间的一致性来标定新题(谭青蓉, 2019)。相比于JEA方法, SIE、SIE-R-BIC和RMSEA-N方法在矩阵标定精度上有一定的提升, 而在标定效率上, 各方法均耗时较长, 新题标定效率相对较低。因此, 在CD-CAT情境下, 开发能提升新题标定精度和标定效率的方法是极为必要的。

数据挖掘作为数据库和人工智能领域研究的热点问题, 其面临的首要问题是如何才能从海量数据中获得有效信息, 从而达到数据信息的高效利用(Chandrashekar & Sahin, 2014)。特征选择(Feature Selection)是有效的解决方法之一, 其可通过删除数据中冗余或无关的特征, 从海量的数据中选择最为有效的特征集, 以达到提高分类准确率以及效率的目的(Guyon & Elisseeff, 2003)。特征选择过程中极为重要的一环是特征选择标准, 其通过衡量特征与分类之间的关系来删除数据中的无关特征。特征选择中使用信息增益、互信息、归一化互信息以及条件互信息等作为特征选择标准, 这类标准通过评估特征的分类准确性来选择最佳的特征(Fleuret, 2004; Hoque et al., 2014; Pereira et al., 2015; Vinh et al., 2012)。特征对被试的分类越精确, 则选择该特征的可能性越高, 若特征对被试的分类相当于随机水平, 则选择该特征的可能性越低。

受数据挖掘中特征选择的启发, 提出如下逻辑假设：在CD-CAT中标定新题时, 可利用特征选择方法来标定新题的矩阵, 并基于该矩阵来估计新题项目参数。将新题所有可能的向量视为待选择的特征, 在被试属性掌握模式已知的情况下, 通过特征选择标准评估每一个可能向量对被试分类的效果, 然后选择能使特征选择标准最佳的向量作为新题的向量。基于该假设, 研究提出一种新的CD-CAT在线标定方法, 该方法基于特征选择方法联合在线标定新题的矩阵和项目参数(该方法的基本过程、思路及公式等将在文章第3部分详细介绍), 以期为CD-CAT在线标定提供新的视角及新的方法, 从而进一步推动认知诊断尤其是CD-CAT在实践中的发展与应用。

2 已有在线标定方法

目前, CD-CAT中同时标定新题矩阵和项目参数的在线标定方法主要有JEA (陈平, 辛涛, 2011b), SIE (Chen et al., 2015), SIE-R-BIC和RMSEA-N方法(谭青蓉, 2019)。SIE方法基于JEA方法在决定型输入噪音与门模型(the Deterministic Input, Noisy and Gate Model, DINA; Junker & Sijtsma, 2001)下提出, 其标定新题时考虑了被试属性掌握模式的估计误差, 在标定新题矩阵和项目参数时充分利用被试的属性掌握模式后验分布。

SIE方法标定新题时包含了矩阵标定和项目参数标定两个部分。对于新题矩阵的标定, 首先基于被试在旧题上的作答计算作答了新题的被试的属性掌握模式后验分布。随后, 根据被试属性掌握模式后验分布及每种属性掌握模式在向量为q的新题上的正确作答概率计算具有某一特定作答R的被试的后验预测分布：

其中为测验测量的属性个数, π(α)表示被试的属性掌握模式为α的概率, 其基于被试在旧题上的作答计算,P(q,g,s,α)表示DINA模型下属性掌握模式为α的被试在项目上的正确作答概率。最后, 结合被试后验预测分布及其在新题上的作答R构建似然并最大化似然函数来估计新题的向量, 其表达式如下：

其中Q= 2− 1表示新题所有可能向量的集合。此外, SIE方法使用EM算法来估计新题的项目参数。

SIE-R-BIC方法在SIE方法的基础上考虑了模型的复杂性, 其估计新题矩阵时构建了BIC指标并通过最小化BIC指标来估计新题向量, 表达式如下所示：

其中log(n)表示模型复杂性的惩罚,表示自由参数的个数,n表示作答新题的被试人数。与此同时, SIE-R-BIC方法在标定新题项目参数时利用了题库中已有项目的信息, 也即将题库中和新题具有相同向量的旧题的项目参数均值作为新题的项目参数初始值。RMSEA-N方法中项目参数的标定与SIE-R-BIC方法一致, 但其通过评估观察作答分布与期望作答分布间的一致性来标定新题的矩阵。具体来说, 选择能使观察作答分布与期望作答分布间一致性程度最高的向量作为新题的估计向量, 其公式如下：

其中(α)表示第个属性掌握模式α的被试边际概率,(α)和(α)分别表示第个属性掌握模式α下标准化的期望正确作答概率和观察正确作答概率。

3 基于熵的信息增益在线标定方法(IGEOCM)

3.1 特征选择方法及基于熵的信息增益

数据挖掘中, 特征选择的目的之一在于选择对数据具有高区分能力的特征, 若基于某一特征的分类与随机分类的结果大同小异, 则说明这一特征对于数据的分类效果较小(李航, 2012)。基于熵的信息增益(Information Gain of Entropy-based, IGE)是特征选择中的一个特征选择准则, 某一特征所具有的基于熵的信息增益值越大, 则其对于数据的分类能力越强(Pereira et al., 2015)。基于熵的信息增益选择最优特征的过程如下：

(1)首先, 确定数据集以及对该数据集进行分类的特征。

(2)然后, 计算数据集的熵

上式中,为数据集的样本量,表示数据集中的类别,n为数据集中属于第个类别的样本量。熵用于评估数据集的不确定性程度, 其值越大, 数据集的不确定性程度越大。不确定性程度指数据集中被试的一致性程度, 若数据集中的被试均属于同一个类别, 则不确定性程度最低。

(3)随后, 计算某一特征对数据集的条件熵

其中,为特征的取值个数,n表示数据集中属于第个类别的被试数量,n表示数据集中第个子类别下, 被试属于第个类别的数量。条件熵用于评估给定某一特征()的情况下, 数据集的不确定性程度。与熵一致, 条件熵的值越大, 数据集的不确定性程度越大, 则基于特征的分类效果越差。

(4)最后, 计算熵的信息增益值

(,) =()–(|). (7)

熵的信息增益(,)为熵与条件熵之差, 其表示在给定特征的信息的情况下, 数据集的不确定性减少的程度。其值越大, 说明基于特征的分类效果越好。

(5)对于所有特征, 重复(3)和(4), 比较各特征的熵信息增益值。选择具有最大的熵信息增益值的特征作为最优特征。

熵的信息增益的大小取决于数据集的熵(())和特征对数据集的条件熵(())。由公式(5)可看出, 数据集的熵值的计算与特征无关, 换句话说, 所有特征下数据集的熵(())均保持不变。因此, 基于熵的信息增益选择特征本质上是基于条件熵选择特征, 某一特征对数据集的条件熵越小, 则该特征的分类效果越好, 该特征更有可能是数据集的最优特征。

新题的向量估计可视为一个特征选择问题, 即从所有可能的向量中为新题选择一个最佳向量。将被试在新题上的作答看作数据集, 新题所有可能的向量看作特征, 基于向量和被试的估计属性掌握模式对被试进行分类, 则能使被试分类的不确定性程度达到最低的向量为作答数据集的最优特征, 因此可选择该向量作为新题的估计向量。基于该思路, 提出新的在线标定方法—基于熵的信息增益的在线标定方法(Information Gain of Entropy-based Online Calibration Method, IGEOCM), 该方法使用熵的信息增益来标定新题的矩阵, 同时使用EM算法来标定新题的项目参数。

3.2 基于熵的信息增益在线标定方法开发

DINA作为广泛应用的认知诊断模型之一, 在每个项目上均只有失误参数和猜测参数这两个简单且易于解释的项目参数, 且常被用于CD-CAT题库的构建及在线标定(Junker & Sijtsma, 2001; Liu et al., 2013)。为了便于说明问题以及与国内外同类方法(SIE方法等)进行比较, 以DINA模型为例来说明基于熵的信息增益的在线标定方法(IGEOCM)标定新题的基本思路及其过程。

3.2.1 IGEOCM中的矩阵标定

当新题所测量的属性个数已知时, 新题所有可能的向量个数为2− 1, 其中不包含元素全为0的向量。从特征选择的视角, 新题的向量估计便是从2− 1种可能向量中选择最合适的一个向量作为新题的估计向量。IGEOCM中基于熵的信息增益这一特征选择准则来估计新题的向量, 其表达式如下所示：

在被试属性掌握模式已知的情况下(即CD-CAT中基于被试在旧题上的作答估计属性掌握模式), 若新题的向量正确且被试在新题上的作答不存在失误和猜测, 那么基于正确向量分类后掌握组中的所有被试在新题上的观察得分都应为1, 而非掌握组中的被试在新题上的观察得分都应为0。此时, 掌握组与非掌握组中的被试都具有高度一致性, 不确定程度最小, 所获得的条件熵(R|q)最小, 信息增益(R,q)最大, 因此正确向量的分类效果最好。若被试的属性掌握模式为均匀分布且被试在新题上的作答不存在失误和猜测, 新题的向量正确和错误情况下(R|q)和(R,q)的变化如表1所示。

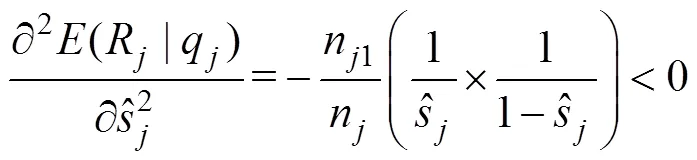
另外, 根据Yu和Cheng (2020)的研究, 当n→∞, 属性掌握模式已知, 且s,g∈(0, 0.5)时, 以下等式成立：

3.2.2 IGEOCM中的项目参数标定

IGEOCM方法中使用EM算法来估计新题的项目参数, EM算法在每一次迭代中都包含期望步骤(Expectation Step, E-step)和最大化步骤(Maximization Step, M-step)两步(Chen et al., 2015)。在E-step中, 首先基于被试在新题上的作答R计算每个被试的后验分布, 其公式如下：

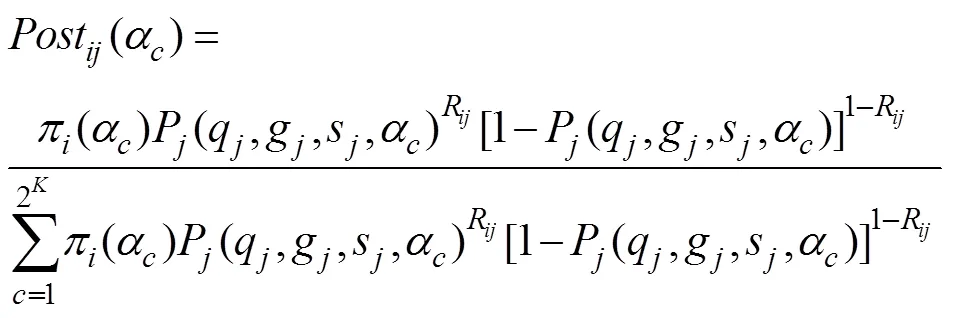
然后, 基于n个被试在新题上的作答向量R和每个被试属性掌握模式的后验分布, 假设n个被试在新题上的作答彼此独立, 可构建对数边际似然函数如下：

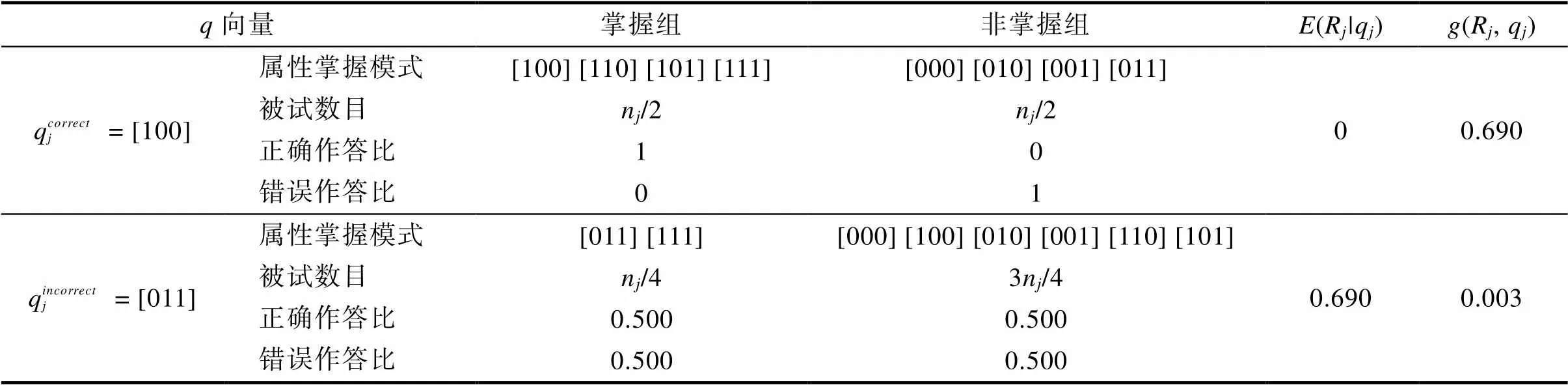
表1 不同q向量下E(Rj|qj)和g(Rj, qj)的计算

M-step的目的在于最大化公式(16)以估计新题的失误参数s和猜测参数g。EM算法依次迭代E-step和M-step直到满足预先设定的收敛标准。

上述两个部分为IGEOCM对新题矩阵和项目参数的标定, 其标定新题的具体步骤如下：

步骤1：新题向量估计。对于新题, 基于作答了新题的被试的属性掌握模式估计值及其在新题上的作答数据, 计算每一个可能向量下作答数据集R的条件熵(R|q), 选择最小(R|q)值对应的向量作为新题的估计向量。

步骤2：新题项目参数估计。将步骤1中的估计向量作为新题的真实向量, 基于作答了新题的被试的属性掌握模式后验分布及其在新题上的作答, 使用EM算法估计新题的失误参数和猜测参数。新题标定完成。

步骤3：对于所有待标定的其他新题, 重复步骤1和步骤2可获得新题的矩阵估计值和项目参数(失误参数和猜测参数)估计值, 直到所有新题标定完成。

IGEOCM是基于特征选择的视角提出的在线标定新方法。该方法的优点在于仅需获得被试的属性掌握模式估计值以及被试在新题上的作答便能估计新题的矩阵, 是一种非参数化的方法, 简单易懂且无需复杂的计算。此外, IGEOCM将基于非参数化方法估计的向量作为新题的真实向量直接标定新题的项目参数, 不论新题可能向量的多少, IGEOCM均只需估计一个已确定向量下的项目参数, 可有效节约项目标定的时间, 改善新题标定的效率。这不同于SIE方法, 其需估计所有可能向量下的项目参数, 标定新题的时间长, 标定新题的效率低。

4 研究1：IGEOCM和已有在线标定方法性能及其精度验证

4.1 实验设计

研究1旨在考查IGEOCM在不同标定样本(40、80、120、160、200)、属性掌握模式分布(均匀分布、高阶分布、多元正态分布)和被试作答新题个数(4、6、8)下标定新题的效果, 并将其与SIE、SIE-R-BIC和RMSEA-N方法进行比较。标定样本指作答了新题的被试人数n= (×)/, 其中,为参与CD-CAT的被试总人数,为每个被试作答新题的个数,为待标定的新题个数(Chen et al., 2015)。选择SIE, SIE-R-BIC和RMSEA-N方法作为比较方法, 主要原因在于其新题标定精度略优于JEA方法, 具有一定的代表性。研究1为四因素实验设计, 共5×3×3×4=180种模拟实验条件, 每种实验条件重复实验500次以减少随机误差。

4.1.1 被试与题库模拟

标定样本共5个水平,n= 40, 80, 120, 160和200, 被试属性掌握模式分别从均匀分布、高阶分布和多元正态分布(0,)中产生。在均匀分布中, 被试的属性掌握模式从所有可能的属性掌握模式中以均匀的概率产生; 在高阶分布中, 被试是否掌握第个属性与被试的一般潜在能力θ有关, 能力为θ的被试掌握第个属性的概率为

其中,0和1为结构参数, λ1> 0。研究中设置= 6, λ= (–1, –0.6, –0.2, 0.2, 0.6, 1), 且对所有属性均有λ1= 1.5, 被试的能力值从(0, 1)中产生(de la Torre & Chiu, 2016); 在多元正态分布中, 属性间的相关设置为0.5 (J. Chen, 2017)。

题库模拟包含项目参数(失误参数和猜测参数g)的模拟和项目矩阵的模拟。题库中共包含300个题目, 每个题目最多测量3个属性, 且题库中测量1、2和3个属性的项目均设置为100题。测验测量属性的总个数= 6, 则共有63种可能的项目向量, 其中测量1个属性的项目向量个数为6, 测量2个属性的项目向量个数为15, 测量三个属性的项目向量个数为20。将测量1个属性的6个项目向量重复16次并从其中额外抽取4个项目向量, 测量2个属性的15个项目向量重复6次并从其中额外抽取10个项目向量, 测量3个属性的20个项目向量重复5次, 构成300×6的临时测验矩阵。最后, 对临时矩阵中的所有行随机排序以获得最后的矩阵。每一个项目的失误参数和猜测参数均从(0.05, 0.25)中随机抽取。

4.1.2 新题模拟

新题的模拟包括新题失误参数和猜测参数的模拟以及新题矩阵的模拟。研究中, 令需标定的新题个数= 24, 因此新题的矩阵是一个24×6的矩阵。新题测验矩阵及其失误参数和猜测参数的模拟均与题库的模拟保持一致。

4.1.3 CD-CAT模拟与新题标定

研究使用定长的终止规则, 每个被试均作答20个旧题和个新题(= 4, 6, 8三个水平)。CD-CAT的模拟过程如下：

测验开始时, 由于对被试的情况一无所知, 因此(1)随机从题库中抽取一个项目作为被试的初始作答项目; (2)模拟当前被试在项目上的作答, 并通过被试在已作答项目上的作答使用MLE估计被试的属性掌握模式; (3)使用后验加权KL (Posterior- Weighted Kullback-Leibler, PWKL; Cheng, 2009)选题策略从剩余题库中挑选最适合被试当前属性掌握模式估计值的项目作为被试的下一个作答项目。重复步骤(2)和(3)直到测验长度达到预先指定的标准。

在CD-CAT模拟过程中, 随机从待标定的24个新题中抽取个新题并将其置于被试测验过程的随机位置。CD-CAT测验结束后, 基于被试的属性掌握模式估计值, 属性掌握模式后验分布及被试在新题上的作答, 分别使用IGEOCM、SIE、SIE-R-BIC和RMSEA-N方法标定新题的矩阵和项目参数。

4.1.4 评价标准

属性向量正确估计率(Attribute Vector Correct Estimation Rate, AVCER) AVCER用于评估新题矩阵的估计正确率, 其表达式为：

均方根误差(Root Mean Squared Error, RMSE) RMSE指标用于评价新题项目参数的估计正确性, 其表达式可写为：

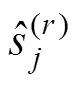
标定效率：即平均运行时间(Average Running Time, ART) ART用于评估各在线标定方法的标定效率, 其计算如下：

其中,t表示第次重复模拟中, 各在线标定方法标定新题所用的时间。ART值越小, 用于标定新题的方法的效率越高。

4.2 实验结果

图1、表2和图2分别呈现了标定方法SIE、SIE-R-BIC、RMSEA-N和IGEOCM的项目标定精度以及标定效率结果。根据Chen等人(2015)的研究, 两方法间标定精度的差值大于等于1%表明一种方法优于另一种方法。总体而言, IGEOCM具有较好的项目标定精度和估计效率, 其性能整体上优于SIE、SIE-R-BIC和RMSEA-N方法。由图1可知, IGEOCM的矩阵估计正确率高于其它三种方法, 属性掌握模式为高阶分布和正态分布时, 各方法间的差异更为明显。如在属性掌握模式为均匀分布时, SIE方法和IGEOCM间的最大AVCER差值为2.3%, 而在属性掌握模式为高阶分布和正态分布时, 两方法间的最大AVCER差值分别高达6.8%和9.1%。SIE和SIE-R-BIC方法的矩阵标定精度在各条件下均较为接近, 而RMSEA-N方法在高阶分布和正态分布下的矩阵标定正确率低于SIE和SIE-R-BIC方法。在属性掌握模式分布对矩阵标定精度的影响上, SIE、SIE-R-BIC、RMSEA-N和IGEOCM的矩阵估计正确率在属性掌握模式为均匀分布时最好, 高阶分布时次之, 正态分布时最差。例如, IGEOCM在均匀、高阶和正态分布下的矩阵估计正确率范围分别为80.9%～99.8%, 67.0%～97.3%和46.0%～76.7%; 而SIE方法在均匀、高阶和正态分布下的矩阵估计正确率范围分别为79.0%～ 99.8%, 60.7%～96.9%和38.4%～68.3%。标定样本对各在线标定方法的矩阵估计正确率影响较大, 标定样本越大, 各方法的矩阵估计正确率越高。当标定样本n= 40时, SIE、SIE-R-BIC、RMSEA-N和IGEOCM的平均AVCER值分别为59.6%、60.0%、45.6%和65.1%, 而当标定样本n= 200时, 4种方法的平均AVCER值上升到88.1%、88.2%、77.2%和91.2%。因此, 增加标定样本可提高各在线标定方法的矩阵估计正确率。SIE、SIE-R-BIC、RMSEA-N和IGEOCM方法在被试作答新题个数为4、6和8的情况下均具有相近的矩阵估计正确率。

图1 各在线标定方法在不同条件下的AVCER (属性向量估计正确率)结果

表2 各在线标定方法在不同条件下的RMSE (均方根误差)结果

图2 各在线标定方法在不同条件下的ART (平均运行时间)结果(单位：秒)

表2为SIE、SIE-R-BIC、RMSEA-N和IGEOCM的项目参数标定结果。SIE方法和IGEOCM在项目参数标定精度上具有相似的性能, 其最大RMSE差值不超过0.2%, 大多数实验条件下两方法的RMSE值相等。SIE-R-BIC方法的RMSE值在标定样本较少时略低于SIE方法和IGEOCM (如,n= 40), 在标定样本较多时略高于SIE方法和IGEOCM (如,n= 200); RMSEA-N方法的RMSE值在多数条件下都高于SIE、SIE-R-BIC和IGEOCM。在属性掌握模式分布对项目参数标定精度的影响上, SIE、SIE-R-BIC和IGEOCM的项目参数标定精度在属性掌握模式为高阶分布时最好, 而RMSEA-N的项目参数标定精度在属性掌握模式为均匀分布时最好。如IGEOCM在高阶、均匀和正态分布下的平均RMSE值分别为0.056、0.066和0.071, RMSEA-N在高阶、均匀和正态分布下的平均RMSE值分别为0.093、0.088和0.142。各方法的项目参数标定精度随标定样本的增加而提升。如, 标定样本n= 40时, SIE方法和IGEOCM的平均RMSE值均为0.11, 而当标定样本n= 200时, 两方法的平均RMSE值均减少为0.04。与矩阵标定精度一致, 被试作答新题个数对SIE、SIE-R-BIC、RMSEA-N和IGEOCM方法项目参数标定精度的影响可忽略不计。

图2为使用SIE、SIE-R-BIC、RMSEA-N和IGEOCM方法估计24个新题的平均运行时间。各模拟条件下, 4种在线标定方法均使用4.0运行, 其计算机配置相同(如Intel Core i5-8400 2.81GHz, 内存20G), 因此各标定方法的估计效率具有可比性。由图2结果可知, 相比于IGEOCM, SIE、SIE-R-BIC和RMSEA-N方法的估计效率更低, 其所有条件下的平均ART值约为IGEOCM的49倍。属性掌握模式分布与被试作答新题个数对SIE、SIE-R-BIC、RMSEA-N和IGEOCM的估计效率影响较小。此外, SIE、SIE-R-BIC、RMSEA-N和IGEOCM的平均运行时间均随标定样本的增加而延长。当标定样本n= 40时, SIE、SIE-R-BIC、RMSEA-N和IGEOCM的平均ART值分别为106.22、93.38、61.39和1.74, 而当标定样本n= 200时, 4种方法的平均ART值延长至414.71、322.40、286.06和6.91。

5 研究2：选题策略对IGEOCM和已有在线标定方法性能的影响

IGEOCM、SIE、SIE-R-BIC和RMSEA-N方法均基于CD-CAT测验中被试属性掌握模式和属性掌握模式后验分布的估计值以及被试在新题上的作答来标定新题, 被试属性掌握模式及属性掌握模式后验分布的估计精度影响各在线标定方法的标定精度(Chen et al., 2015)。而CD-CAT中, 选题策略是影响被试属性掌握模式估计精度的重要因素之一。因此, 研究2在研究1的基础上, 进一步考察选题策略对各在线标定方法性能的影响。

5.1 实验设计

研究2的实验设计和模拟过程与研究1基本一致, 但研究2在研究1的基础上新增了MPWKL (the modified PWKL)、GDI (the generalized deterministic inputs, noisy and gate (G-DINA) model discrimination index)和香农熵(Shannon entropy, SHE)选题策略(Cheng, 2009; Kaplan et al., 2015), 以比较IGEOCM和SIE方法在不同选题策略下的可行性和准确性。由于SIE和SIE-R-BIC方法的项目标定精度略高于RMSEA-N方法, 且SIE方法的项目参数标定精度在多数条件下均略高于SIE-R-BIC和RMSEA-N方法。另外, 三者在标定效率上差异较小, 均耗时较长(ART比值不超过1倍), 因此研究2中仅选择已有方法SIE作为新方法IGEOCM的比较方法。此外, 基于研究1的结果, 被试新题作答个数对SIE方法和IGEOCM项目标定精度的影响较小, 研究2中将被试作答新题的个数固定为6 (= 6)。考虑到SIE方法和IGEOCM的运行时间随标定样本的增加而延长, 因此研究2中将标定样本固定为40以缩短实验时长。其余实验条件和模拟过程请参见研究1。

5.2 实验结果

表3为SIE方法和IGEOCM在不同选题策略和不同属性掌握模式分布下的项目标定精度与标定效率结果。与研究1结果相似, 相比于SIE方法, IGEOCM在各选题策略下均具有更高的项目标定精度和项目估计效率。此外, 在所有选题策略下,SIE和IGEOCM方法的矩阵估计正确率在属性掌握模式为均匀分布时最好, 高阶分布时次之, 正态分布时最差。

CD-CAT选题策略对在线标定方法的新题矩阵标定精度有一定影响。如属性掌握模式为高阶分布的情况下, SIE方法在选题策略为MPWKL时具有较高的矩阵标定精度, 其AVCER值为61.7%; SIE方法在选题策略为PWKL时具有较低的矩阵标定精度, 其AVECR值为60.7%。在属性掌握模式为正态分布的情况下, IGEOCM方法在选题策略为GDI时具有较高的矩阵标定精度, 其AVCER值为46.7%; IGEOCM方法在选题策略为PWKL时具有较低的矩阵标定精度, 其AVECR值为45.4%。CD-CAT选题策略对新题项目参数和估计效率的影响可忽略不计。各选题策略下的RMSE均值之差不超过0.2%, 平均运行时间(ART)较为接近。

6 总结与讨论

CD-CAT中同时标定新题矩阵和项目参数的在线标定方法较少, 且均为参数化的方法, 标定新题的时间较长, 标定效率较低。因此, 研究借鉴数据挖掘中特征选择(Feature Selection)的思路, 提出了基于熵的信息增益的在线标定方法(IGEOCM), 以期为CD-CAT题库中项目的增补提供一种更为高效、准确的方法。不同于CD-CAT中已有的在线标定方法, IGEOCM使用非参数的方法标定新题的矩阵, 较为有效地避免了项目参数估计偏差所带来的影响, 改善了项目标定的精度, 同时提高了项目标定的效率。随后, 使用Monte Carlo模拟研究来验证IGEOCM的可行性和准确性, 并将其与已有在线标定方法SIE、SIE-R-BIC和RMSEA-N进行比较。研究结果表明：(1) IGEOCM在各条件下均具有较好的项目标定精度和项目估计效率, 且整体上优于SIE、SIE-R-BIC和RMSEA-N方法。SIE等方法基于新题项目参数的估计值来估计新题矩阵, 项目参数的估计误差影响新题矩阵的标定精度, 继而降低新题标定精度; 而IGEOCM基于被试属性掌握模式及其在新题上的作答直接标定新题矩阵, 新题矩阵的标定与项目参数的估计精度无关, 额外影响因素少, 新题标定精度更高一些。此外, 尽管SIE和IGEOCM项目参数估计方法一致, 但SIE方法使用参数化方法标定新题矩阵, 而IGEOCM方法使用非参数化方法标定新题矩阵。相比参数化方法, 非参数化方法计算更为简单, 运行时间更短(Chiu et al., 2018), 因此IGEOCM的新题标定效率较好一些。(2) SIE、SIE-R-BIC、RMSEA-N和IGEOCM的项目标定精度随标定样本的增加而提高, 4种方法的运行时间随标定样本的增加而延长。(3) SIE、SIE-R-BIC、RMSEA-N和IGEOCM在属性掌握模式分布为均匀分布和高阶分布时的项目标定精度高于正态分布。(4)被试作答新题个数对SIE、SIE-R-BIC、RMSEA-N和IGEOCM项目标定精度和估计效率的影响较小。(5) CD-CAT中选题策略影响SIE方法和IGEOCM的矩阵标定精度。在属性掌握模式为高阶和正态分布时, 相比PWKL选题策略, SIE方法和IGEOCM在选题策略分别为MPWKL和GDI时的矩阵标定精度略高。此外, 研究还考察了属性掌握模式为高阶分布时不同的λ0和λ1模拟方式对SIE方法和IGEOCM的影响, 即λ0从标准正态中产生和λ1从对数标准正态分布中产生, 在被试作答新题个数固定为6, 其余条件与研究1相同的情况下：IGEOCM在该模拟方式下仍优于SIE方法。该结果进一步表明IGEOCM的可行性及其优势(具体数据结果参见网络版附表1)。

表3 SIE方法和IGEOCM在不同条件下的项目标定精度与标定效率结果

当然, 研究仍有许多不足之处, 今后研究中需加以改进与完善。首先, 文中仅验证了所提出IGEOCM在DINA模型下的性能, 其在较为复杂的认知诊断模型, 如缩减重新参数化融合模型(the Reduced Reparametrized Unified Model, RRUM; Hartz, 2002), 拓广DINA (the Generalized Deterministic Inputs, Noisy and Gate Model, G-DINA; de la Torre, 2011)等模型下的性能仍有待进一步探讨。不同于DINA模型, 其仅将被试分为掌握与非掌握两个类别。在更为复杂的模型下, 基于被试属性掌握模式和项目向量可以将被试划分为更多不同的类别, 而基于熵的信息增益指标会随着被试所划分类别的增加而增加, 因此在更为复杂的认知诊断模型下使用基于熵的信息增益指标来标定新题向量的效果值得探讨。未来研究中可考虑如何解决被试类别数量对IGEOCM的影响, 如对被试类别数进行惩罚以减少类别个数对IGEOCM的影响。

其次, CD-CAT中已有的在线标定方法均是基于二级计分模型。实际上, 心理与教育评估中存在大量的多级计分数据以及多级计分题目, 且相比于二级计分的作答数据, 多级计分的作答数据可为被试提供更为全面详尽的诊断信息。文中所提出的在线标定方法应如何推广到系列G-DINA模型(sequential G-DINA model; Ma & de la Torre, 2016)等多级计分模型之中, 并验证其在多级计分模型下的性能有待进一步研究。

再次, 研究为每个被试随机选择新题, 用于标定每个新题的被试可能并非最合适的被试。未来研究中可考虑使用自适应的方法来为每个项目选择最合适的被试, 比如使用最优设计准则来为每个项目选择最佳被试(He et al., 2020)。然后考察不同的新题选择方式(随机选择和自适应选择)对在线标定方法的影响。

最后, 研究假设测验所测量的属性之间相互独立。然而, 在实际的诊断测验中, 属性之间可能存在各种层级关系, 比如无结构型、线型、分支型和收敛型(Leighton et al., 2004)。因此, 未来研究一个可考虑的方向是探讨不同属性层级关系对在线标定方法的影响。另外, 研究使用模拟实验验证所提出的矩阵与项目参数在线标定方法的科学性与合理性, 虽然模拟研究的结果能为实践应用提供一定指导, 但模拟研究是在理想的情境下进行, 会忽略很多真实情境中的影响因素, 因此未来研究需进一步评估真实情境中各在线标定方法的性能。总之, CD-CAT中同时标定新题矩阵与项目参数的在线标定方法仍需进一步的研究。

Ban, J. C., Hanson, B. A., Wang, T., Yi, Q., & Harris, D. J. (2001). A comparative study of on-line pretest item— Calibration/scaling methods in computerized adaptive testing.,(3), 191–212.

Chandrashekar, G., & Sahin, F. (2014). A survey on feature selection methods.,(1), 16–28.

Chen, J. (2017). A residual-based approach to validate Q-matrix specifications.,(4), 277–293.

Chen, P. (2016). Two new online calibration methods for computerized adaptive testing.,(9), 1184–1198.

[陈平. (2016). 两种新的计算机化自适应测验在线标定方法.,(9), 1184–1198.]

Chen, P. (2017). A comparative study of online item calibration methods in multidimensional computerized adaptive testing.,(5), 559–590.

Chen, P., & Wang, C. (2015). A new online calibration method for multidimensional computerized adaptive testing.,(3), 674–701.

Chen, P., Wang, C., Xin, T., & Chang, H. H. (2017). Developing new online calibration methods for multidimensional computerized adaptive testing.,(1), 81–117.

Chen, P., & Xin, T. (2011a). Developing on-line calibration methods for cognitive diagnostic computerized adaptive testing.,(6), 710–724.

[陈平, 辛涛. (2011a). 认知诊断计算机化自适应测验中在线标定方法的开发.,(6), 710–724.]

Chen, P., & Xin, T. (2011b). Item replenishing in cognitive diagnostic computerized adaptive testing.,(7), 836–850.

[陈平, 辛涛. (2011b). 认知诊断计算机化自适应测验中的项目增补.,(7), 836–850.]

Chen, P., Xin, T., Wang, C., & Chang, H. H. (2012). Online calibration methods for the DINA model with independent attributes in CD-CAT.,(2), 201–222.

Chen, Y., Liu, J., & Ying, Z. (2015). Online item calibration for Q-matrix in CD-CAT.,(1), 5–15.

Cheng, Y. (2009). When cognitive diagnosis meets computerized adaptive testing: CD-CAT.,(4), 619–632.

Chiu, C. Y., Sun, Y., & Bian, Y. (2018). Cognitive diagnosis for small educational programs: The general nonparametric classification method.,(2), 355–375.

de la Torre, J. (2011). The generalized DINA model framework.,(2), 179–199.

de la Torre, J., & Chiu, C. Y. (2016). A General method of empirical Q-matrix validation.,(2), 253–273.

Fleuret, F. (2004). Fast binary feature selection with conditional mutual information.,(11), 1531–1555.

Guyon, I., & Elisseeff, A. (2003). An introduction to variable and feature selection.,(3), 1157–1182.

Hartz, S. M. (2002).(Unpublished doctoral dissertation). University of Illinois at Urbana-Champaign.

He, Y., Chen, P., & Li, Y. (2020). New efficient and practicable adaptive designs for calibrating items online.,(1), 3–16

Hoque, N., Bhattacharyya, D. K., & Kalita, J. K. (2014). MIFS-ND: A mutual information-based feature selection method.,(14), 6371–6385.

Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory.,(3), 258–272.

Kaplan, M., de la Torre, J., & Barrada, J. R. (2015). New item selection methods for cognitive diagnosis computerized adaptive testing.,(3), 167–188.

Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka's rule-space approach.,(3), 205–237.

Li, H. (2012).. Beijing: Tsinghua University Press.

[李航. (2012).. 北京: 清华大学出版社.]

Liu, H. Y., You, X. F., Wang, W. Y., Ding, S. L., & Chang, H. H. (2013). The development of computerized adaptive testing with cognitive diagnosis for an English achievement test in China.,(2), 152–172.

Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses.,(3), 253–275.

Pereira, R. B., Plastino, A., Zadrozny, B., & Merschmann, L. H. (2015). Information gain feature selection for multi-label classification.,(1), 48–58.

Rupp, A. A., & Templin, J. L. (2008). The effects of Q-matrix misspecification on parameter estimates and classification accuracy in the DINA model.,(1), 78–96.

Stocking, M. L. (1988). Scale drift in on-line calibration.,(1), 1–122.

Tan, Q. (2019).(Unpublished master’s thesis). Jiangxi Normal University, Nanchang, China.

[谭青蓉. (2019).(硕士学位论文). 江西师范大学, 南昌.]

Vinh, L. T., Lee, S., Park, Y. T., & d’Auriol, B. J. (2012). A novel feature selection method based on normalized mutual information.,(1), 100–120.

Wainer, H., & Mislevy, R. J. (1990). Item response theory, item calibration, and proficiency estimation. In H. Wainer (Ed),:(Chap. 4, pp. 65–102). Hillsdale, NJ: Erlbaum.

Wang, C. (2013). Mutual information item selection method in cognitive diagnostic computerized adaptive testing with short test length.,(6), 1017–1035.

Weiss, D. J. (1982). Improving measurement quality and efficiency with adaptive testing.,(4), 473–492.

Yu, X., & Cheng, Y. (2020). Data-driven Q-matrix validation using a residual-based statistic in cognitive diagnostic assessment.,(Suppl 1), 145–179.

附录：

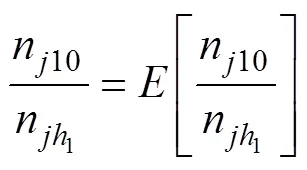
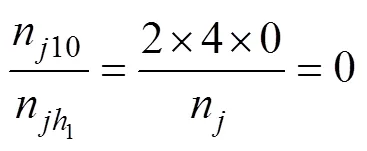
然后(R|)可计算如下

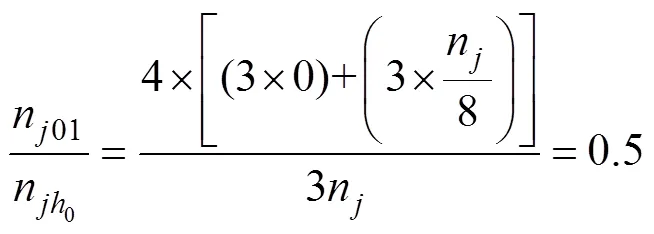
然后(R|)可计算如下

由上述例子可知, 在新题的向量正确时,(R|)最小, 其值为0, 此时熵的信息增益(R,q)达到最大。因此, 在新题向量未知的情况下, 可以选择能使熵的信息增益(R,q)最大的向量作为新题的估计向量。

附表1 不同λ0和λ1产生方式下SIE和IGEOCM方法的项目标定精度

方法4080120160200 AVCER条件1SIE0.5890.7860.8600.8970.920 IGEOCM0.6410.8230.8850.9130.938 条件2SIE0.6060.8120.8960.9420.965 IGEOCM0.6680.8570.9160.9500.966 RMSE条件1SIE0.1340.0880.0680.0580.051 IGEOCM0.1320.0850.0690.0600.052 条件2SIE0.0950.0620.0490.0410.037 IGEOCM0.0950.0620.0490.0410.037

注：条件1表示λ0和λ1分别从正态分布和对数正态分布中产生; 条件2表示设置λ= (–1, –0.6, –0.2, 0.2, 0.6, 1), 且对于所有属性均有λ1= 1.5。

A high-efficiency and new online calibration method in CD-CAT based on information gain of entropy and EM algorithm

TAN Qingrong, WANG Daxun, LUO Fen, CAI Yan, TU Dongbo

(School of Psychology, Jiangxi Normal University, Nanchang 330022, China)

Cognitive diagnostic computerized adaptive testing (CD-CAT) includes the advantages of both cognitive diagnosis (CD) and computerized adaptive testing (CAT), which can offer detailed diagnosis feedback for each examinee by applying fewer test items and time. It has been a promising field. An item bank is a prerequisite for the implementation of CD-CAT. However, its maintenance is a very challenging task. One of the effective ways to maintain the item bank is online calibration. Till now, there are only a few online calibration methods in the CD-CAT context that can calibrate Q-matrix and item parameters simultaneously. Moreover, the computational efficiency of these methods needs to be further improved. Therefore, it is crucial to find more online calibration methods that jointly calibrate the Q-matrix and item parameters.

Inspired by the SIE (Single-Item Estimation) method proposed by Chen et al. (2015) and information gain feature selection criteria in feature selection, an information gain of entropy-based online calibration method (IGEOCM) was proposed in this study. The proposed method can jointly calibrate Q-matrix and item parameters in a sequential manner. The calibration process of the new items was described as follows: First, for the new item, the q-vector can be calibrated by maximizing the information gain of entropy-based on the basis of the attribute patterns of examinees and the examinees’ responses to item. Second, the item parameters of the new itemare estimated by the EM algorithm based on the posterior distribution of examinees’ attribute pattern, the examinees’ responses to item, and the q-vector estimated in the first step. The first and second step are repeated for all other new items to obtain their estimated Q-matrix and item parameters item by item. Two simulation studies were conducted to examine whether the IGEOCM could accurately and efficiently calibrate the Q-matrix and item parameters of the new items under different calibration sample sizes (40, 80, 120, 160, and 200), different attribute pattern distributions (uniform distribution, higher-order distribution, and multivariate normal distribution), the different number of new items answered by examinee (4, 6, and 8), and different item selection algorithms (posterior-weighted Kullback-Leibler, PWKL; the modified PWKL, MPWKL; the generalized deterministic inputs, noisy and gate model discrimination index, GDI; and Shannon entropy, SHE). Furthermore, the performance of the proposed method was compared with the SIE, SIE-R-BIC, and RMSEA-N methods.

The results indicated that (1) The IGEOCM worked well in terms of the calibration accuracy and estimation efficiency under all conditions, and outperformed the SIE, SIE-R-BIC, and RMSEA-N methods overall. (2) The accuracy of the item calibration increases as the sample size increases for all calibration methods under all conditions. (3) The SIE, SIE-R-BIC, RMSEA-N, and IGEOCM performed better under the uniform distribution and higher-order distribution than under the multivariate normal distribution. (4) The number of new items answered by the examinee had a negligible impact on the calibration accuracy and computation efficiency of the SIE, SIE-R-BIC, RMSEA-N, and IGEOCM. (5) The item selection algorithm in CD-CAT affects the Q-matrix calibration accuracy of the SIE and IGEOCM methods. Under the higher-order distribution and multivariate normal distribution, the SIE method and IGEOCM had higher Q-matrix calibration accuracy when the item selection algorithms were MPWKL and GDI.

On the whole, although the proposed IGEOCM is competitive and outperforms the conventional method irrespective of the calibration precision or computational efficiency, the studies on the online calibration method in CD-CAT still need to be further deepened and expanded.

cognitive diagnostic computerized adaptive testing, item replenishing, online calibration, Q-matrix, information gain of entropy

B841

2020-11-30

* 国家自然科学基金项目(31760288, 31960186, 31660278)。

涂冬波, E-mail: tudongbo@aliyun.com; 蔡艳, E-mail: cy1979123@aliyun.com