泛函积分方法与非Gauss随机散射通道模型中传递函数的概率分布计算

周良建， 颜 骏， 赵 丰， 詹 路

（四川师范大学 物理与电子工程学院，四川 成都610066）

发射信号在传播中经物体反射后，原始的入射信号振幅将发生改变，通过入射波与反射波的振幅差异可以得到波反射的位置、运动状态和散射体性质等信息.雷达的目标探测、地貌探测等大多数物理应用，都是基于对发射和接收信号的各种对比.信号传播和散射的物理模型通常都是根据经验结果所总结出的现象学理论，因此，具有一定的实用价值.但是由于散射系统环境可能具有的不确定性，所以在理论研究中，除了包含确定成份之外，还应研究散射通道中随机成份的影响，这在处理雷达信号中也是必须考虑的因素［1］.

传递函数τ（ω）可以描述散射截面的随机性对信号波传输的影响，这类函数是由频率为ω的发射波和反射波振幅比来定义的物理量，它与散射体截面平方根成正比关系，与散射体到发射器和接收器的距离成反比关系.本文将引入复空间散射振幅密度ρ（r）来描述散射体截面的强弱［2］，然后由密度和衰减函数乘积的体积分来重新表示传递函数.根据传递函数中的实部和虚部的δ函数乘积，可进一步定义其密度泛函空间上的概率分布.通过对Dirac-δ函数进行傅里叶变换后导出带有辅助积分变量的特征函数，为了计算出这一函数的具体表达式，需要给出散射振幅密度的概率分布形式.由于作用量中除了含有随机场ρ（r）的2次型函数，还包括了线性项的贡献，为了对特征函数中密度场完成泛函积分，可以借助于散射振幅密度的Shift变换来消除线性项的影响.

本文还将采用泛函积分方法计算散射系统传递函数概率分布的具体形式.泛函积分是理论物理中一种有效的数学工具，在量子场论、统计物理、固体物理、湍流理论等领域中有广泛的应用［3-9］，特别是量子力学中的路径积分方法可用于研究随机介质中波传播过程的各种物理现象.Filinov［10-12］采用修正路径积分和复蒙特卡罗方法分析了色散介质中波的传播，Constantinou等［13］根据路径积分方法讨论了随机不均匀波导中的传输过程，文献［14-15］使用路径积分近似方法计算了混浊介质中光子的传播问题.最近，Cabrera等［16］根据场论中的泛函积分方法导出了随机散射中传递函数的概率分布，结果发现当随机散射密度遵从Gauss位形分布时，那么传递函数的概率将满足2维正态分布形式.除了泛函积分方法之外，随机泛函分析方法也被应用于随机介质中波的传播特征和局域化现象［17］.

在一般的物理模型中，都假定随机变量遵从Gauss分布或正态分布，这时可以用期望值、方差和协方差来分别描述随机量的平均值，涨落大小和关联效应.在实际问题中遇到的许多随机现象中并不严格遵从Gauss分布，或都服从近似正态分布，如水面的波峰和波谷通常具有不同形状，导致散射声波基本上是非Gauss的环境表面［18］.另外，由于湍流的阵发性或间歇性质，表现在统计特性上对Gauss分布的偏离，所以要用非Gauss随机介质中统计矩方程来研究传播光场的统计性质［19］.

本文将引入随机外源来研究非Gauss散射通道模型中传递函数的概率分布，进一步给出随机变量方差和协方差矩阵元的修正表达式.当散射振幅密度的关联函数取为Dirac-δ函数形式时，计算不同位置点的方差，协方差以及相关系数的具体数值，讨论了这些概率量的物理含义和变化规律，分析非Gauss外源的作用系数确定时，衰减函数中振荡指数对相关系数的影响.

1 传递函数概率分布的泛函积分表示

如果有一个振幅为T（t）的信号波在位置rT处发射、在rR处被接收，并且在传播过程中信号波与N个点发生散射，那么通过散射后的信号波振幅可表示为［16］

表示散射系统的传递函数，这一物理量描述了散射体对频率为ω的传输信号产生的影响，体积元中的散射振幅密度的模定义为

表示信号波传输过程中的相位变化及衰减程度，（5）式中下标ρ表示τρ是与散射振幅密度ρ（r）相关的传递函数.通常散射截面越大那么散射振幅密度越高，对传输信号影响所产生的影响更为显著，因此信号波传播中振幅的变化与散射振幅密度ρ（r）和函数H（r）都有密切关系.如果散射截面有一定的不确定性，那么散射振幅密度ρ（r）就可能具有随机函数的性质，因此可以用密度泛函空间上的概率分布理论加以描述.

传递函数的概率分布可以用Dirac-δ函数的平均值表示为

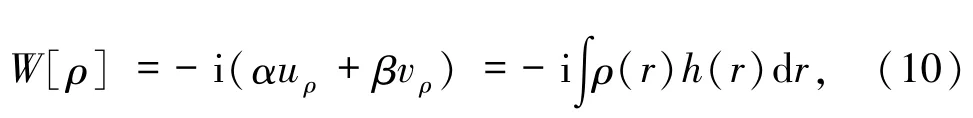
其中衰减函数为定义为h（r）＝αf（r）＋βg（r），在第2节中将研究非Gauss型散射系统中传递函数的概率分布.假定散射通道模型中的振幅密度遵从复随机场的非Gauss分布，然后根据泛函积分方法推导和计算了传递函数概率分布矩阵元的修正形式和具体数值.

2 非Gauss密度分布下传递函数的概率分布

其中随机密度场类似于量子统计物理中的复玻色场.（15）式指数中积分项都是关于随机场ρ（r）的或外源的2次型函数，这些二次项来自于非Gauss分布F［ρ］中的指数项，而线性项则来源于W［ρ］，为了对特征函数中密度场完成泛函积分，可将随机场进行Shift变换其中

这种技巧类似于玻色凝聚中的Popov-Faddeev正则变换［20］，已被用于计算高温超导模型的准粒子激发谱［7，21］.根据这一变换可以得到如下等式

另外积分测度不发生变化，所以有Dρ＝D.将（17）式代入（15）式将分母项消除，然后再对随机场场进行泛函积分有

虽然散射振幅密度遵从非Gauss型的概率分布，但是传递函数的概率将依然满足2维正态分布形式，不过方差和协方差都将受到随机外源的微扰影响.其中，方差表示随机变量u、v的涨落大小和趋势，协方差表示随机变量的关联效应，相关系数定义为

当积分核、衰减函数和外源作用系数分别确定后，便可以计算出传递函数概率分布中修正矩阵元和相关系数的具体数值.

3 修正矩阵元和相关系数的数值计算

为了计算出1阶微扰修正矩阵元的数值，可将关联函数取成Dirac-δ函数形式，即¯K（r，r′）＝k0δ（r－r′），其中k0是权重系数.并进一步设衰减函数具有如下振荡模式

r0为的散射体与发射点的距离.对于单站位形，仅保留1阶微扰的贡献，当振荡指数m、n从1到2分别取值，并且取＝0.8时，那么可以计算出正规化矩阵元和相关系数的具体数值，如表1～4所示，其中不带横线的量表示Gauss型分布时的矩阵元和相关系数.

表1 当振荡指数和作用系数取为m＝1，n＝1，¯ε＝0.8时，修正矩阵元和相关系数的计算值Tab.1 The corrected matrix elements and correlation coefficients when the oscillation exponents and the action coefficient are taken as m＝1，n＝1，¯ε＝0.8

表2 当振荡指数和作用系数取为m＝2，n＝2，¯ε＝0.8时，修正矩阵元和相关系数的计算值Tab.2 The corrected matrix elements and correlation coefficients when the oscillation exponents and the action coefficient are taken as m＝2，n＝2，¯ε＝0.8

表3 当振荡指数和作用系数分别取为m＝1，n＝2，¯ε＝0.8时，修正矩阵元和相关系数的计算值Tab.3 The corrected matrix elements and correlation coefficients when the oscillation exponents and the action coefficient are taken as m＝1，n＝2，¯ε＝0.8

表4 当振荡指数和作用系数分别取为m＝2，n＝1，¯ε＝0.8时，修正矩阵元和相关系数的计算值Tab.4 The corrected matrix elements and correlation coefficients when the oscillation exponents and the action coefficient are taken as m＝2，n＝1，¯ε＝0.8

从表1～4可以看出，当无量纲距离x由小变大时，修正前后的矩阵元均呈振荡变化趋势，其中，对角矩阵元G11、G22为正值，修正后的矩阵元数值增大；非对角矩阵元G12可取正值，也可取负值，修正前后的矩阵元既可以同号，也可以反号.当m＝1，n＝1或m＝1，n＝2时，修正前后的相关系数符号可以相同，也可以改变符号；当m＝2，n＝2或m＝2，n＝1时，那么修正前后的相关系数符号完全相同.另外，根据表1～4的计算结果还可以大致判定出随机变量的相关程度，当m＝1，n＝1时，修正前后的相关系数都很小，表示一种极弱关联情况，当m＝1，n＝2或m＝2，n＝1时，相关系数都较小，相关程度介于极弱关联和弱关联之间，当m＝2，n＝2相关系数变大，这时关联程度介于弱关联和中等关联之间.所以，当振荡指数之和较小时，微扰修正可以相关系数符号，当振荡指数之和变大时，那么微扰修正可以明显该变关联程度的等级.

4 结论与讨论

本文引入了复空间散射振幅密度这一随机函数，并假设散射振幅密度满足非Gauss型的概率分布.根据泛函积分方法导出了传递函数概率分布矩阵元的微扰修正表达式，这类传递函数可描述随机散射物体对传输信号产生的影响.

当散射振幅密度的关联函数取为Dirac-δ函数形式时，通过数值方法进一步计算了不同振荡指数下无量纲矩阵元和相关系数的具体数值，结果发现修正前后的矩阵元随无量纲距离x变大而呈现振荡变化趋势.当m＝1，n＝1，或m＝1，n＝2时，微扰修正前后的相关系数可以改变符号，即由正相关变为负相关，或由负相关变为正相关，这一结果描述了Gauss型和非Gauss型传递函数中随机变量的不同关联趋向.当m＝2，n＝2，或m＝2，n＝1时，那么微扰修正前后的相关系数符号完全相同，表示传递函数中随机变量具有相同的关联趋向.

当振荡指数和由小增大时，相关系数由很小的值变为较大的值，这时传递函数中随机变量由极弱关联、弱关联逐渐变为中等关联.当无量纲作用系数确定时，随着振荡指数和变大，那么在非Gauss型传递函数中随机变量关联程度等级也将增强.

本文重点研究了非Gauss通道模型中散射振幅密度的概率分布，借助解析方法和数值计算技术，推导和计算了传递函数概率分布中矩阵元的修正形式和具体数值，比较了Gauss分布和非Gauss分布情况下的相关系数和关联趋向.泛函积分方法并不仅可用来描述Gauss散射通模型中的随机现象，它也可用于非Gauss散射情况下的传递函数的计算.目前，这一方法已广泛应用于量子场论和量子统计物理学的研究，同时也适用描述于经典物理中的各种现象，如流体中湍流分布，随机介质中波的传播，以及散射体对信号波传播的影响等物理课题.