基于状态观测器的混沌系统滑模控制
2021-11-15孙春香李冠军
孙春香, 杜 珺, 李冠军
(淮南师范学院 金融与数学学院,安徽 淮南232038)
混沌控制自从1990年由Ott等[1]提出,就受到了广泛的关注,因为它在许多领域都具有重要的应用前景.学者们给出了很多有效的控制方法,如自适应控制[2-3]、反馈控制[4-5]、模糊控制[6-7]、滑模控制[8-9]、反推控制[10-11]等,并将其应用到实际工程技术中,如摆振控制[12]、机器人控制[13].
滑模控制是基于变结构系统理论的一种控制方法,由于对非线性系统具有很好的鲁棒性,并且具有响应速度快、暂态性能好以及对植物参数变化、外部干扰不敏感等优点,从而在工程中得到广泛的应用,吸引了研究者们的注意[14-18].文献[19]针对具有不可用状态的非线性多变量系统,采用模糊自适应技术和滑模控制相结合的方法,设计了一个稳定的自适应模糊滑模控制器.在许多混沌系统中,不可避免地会受到未知参数变化和外界干扰的影响,滑模变结构控制在同步控制器设计中得到了广泛应用.文献[20]中研究了具有参数不确定的2个混沌系统的滑模动态同步控制方法;文献[21]研究了不同时变条件下,具有未知参数的Rossler和Chen混沌系统的鲁棒自适应同步问题,而文献[22]则研究了基于滑模观测器的非线性系统故障诊断问题.
在已有文献研究的滑模控制中,大多数要求系统的状态变量是已知的,然而这在实际工程领域是很难实现的.通常情况下,状态变量是未知的或部分未知的.因此,上述通过状态反馈的控制策略就很难实现,所以需要利用观测器对状态变量进行估计,基于观测器的智能自适应滑模控制方法是一个非常必要的控制策略.
基于上述讨论,本文主要研究Genesio系统的自适应滑模控制,在状态变量未知的情况下,构造观测器,对未知变量估计,利用估计值建立滑模控制策略,使得控制系统是指数渐进稳定的,并且观测器和追踪误差是指数趋于0.
1 系统描述
Genesio系统由Genesio和Tesi[23]提出的一类比较典型的非线性混沌系统,可以表示为
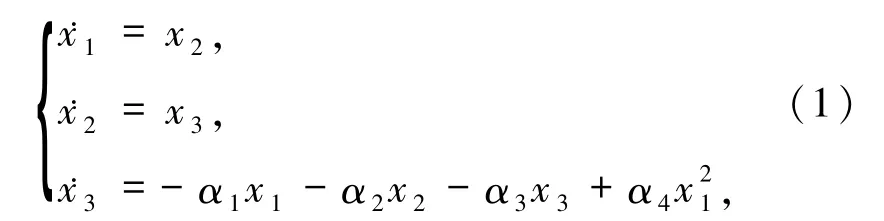
其中,x1、x2、x3是系统状态变量,α1、α2、α3、α4是系统参数.当选择α1=1.2、α2=2.92、α3=6、α4=1,初值为x1=1、x2=1、x3=-1时,Genesio系统呈现混沌状态,如图1所示.对于Genesio混沌系统,文献[24]利用迭代变换法讨论了Genesio系统的同步问题,给出了同步流形的稳定性的充分条件;文献[25]提出了自适应同步控制方案,基于Lyapunov方法,使2个Genesio-Tesi系统的状态渐近同步,给出了基于线性矩阵不等式的控制律存在性判据.
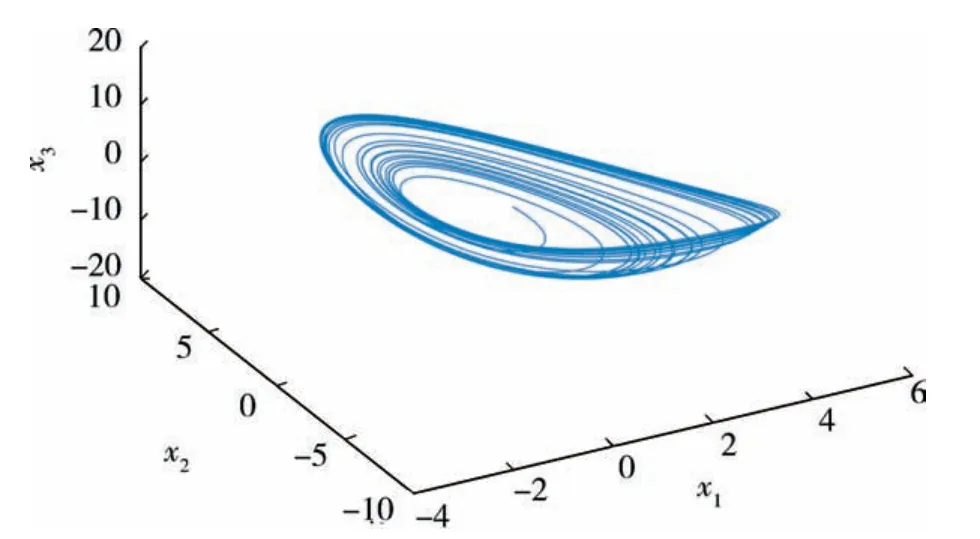
图1 Genesio系统(1)混沌吸引子Fig.1 The chaotic attractor of Genesio system(1)
2 滑模控制器设计及稳定性分析
2.1 传统滑模控制器设计 设计滑模控制器,使混沌Genesio系统(1)的轨迹到达理想信号xd.下面给出一些有用的引理.

定理1对于系统(2),设计滑模面(3)和滑模控制器(4),则存在正常数k和γ,使得当t→∞时追踪误差ei指数收敛于0,i=1,2,3.
证明由(2)和(3)式可得
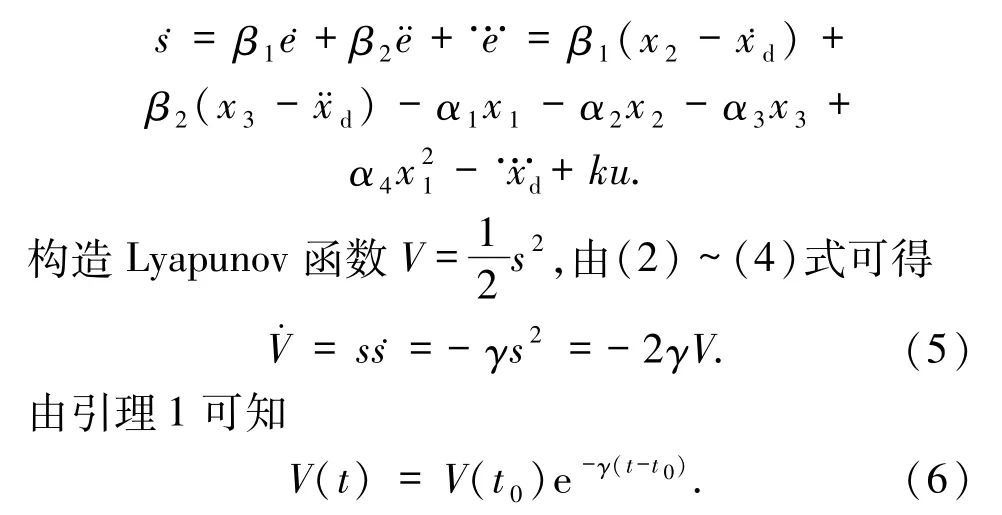
从(6)式可知,当t→∞,追踪误差是指数收敛0,并且收敛速度由常数η确定.
注1滑模函数(3)和控制器(4)的设计都依赖于状态变量x1、x2、x3.因此,只有当这些状态变量是已知的情况下,该控制策略才能实现.
为了说明设计的滑模控制方法有效性,对(2)式,假设理想信号
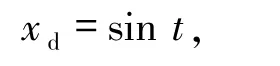
滑模函数和控制器分别是(3)和(4)式给出的形式,选择β1=8、β2=16、γ=4、k=4,从图2~图5中可以看出所设计的滑模控制器在混沌系统控制中,具有非常好的效果.图2给出了追踪信号xi和理性信号xd的状态轨迹,可以看出它们在较短的时间内就可以达到同步;而图5中反映了追踪误差趋于0.
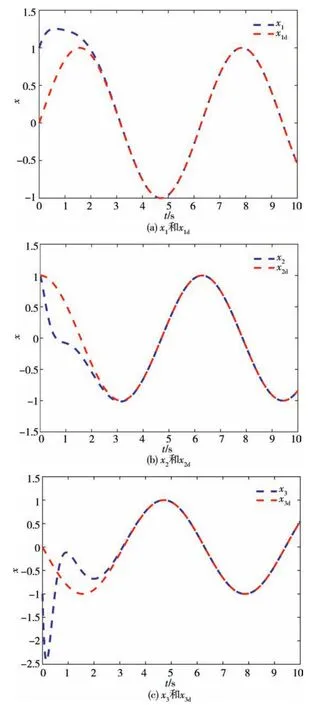
图2 理想信号和追踪信号的状态轨迹Fig.2 The state trajectories of ideal signal and tracking signal
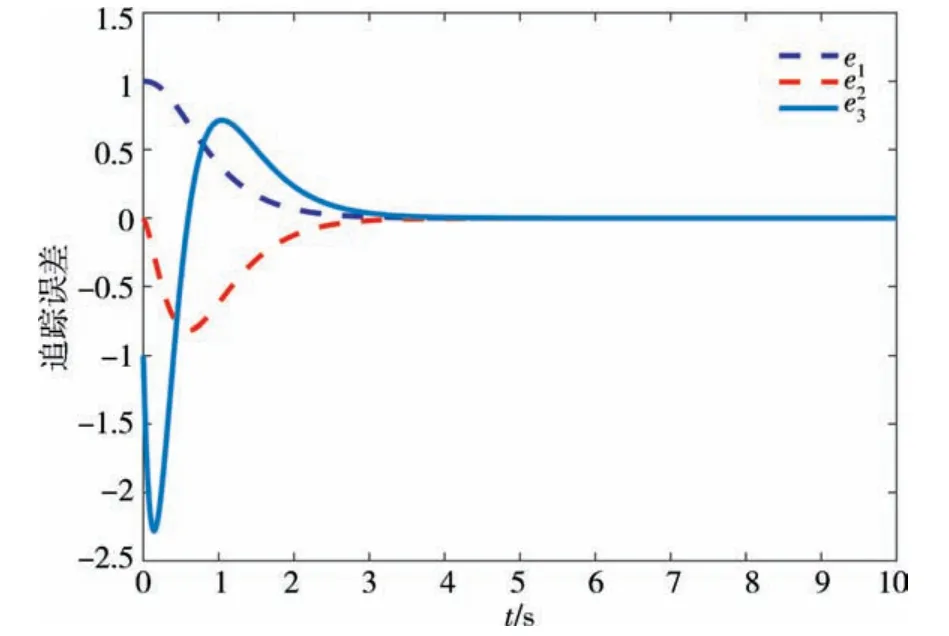
图5 追踪误差Fig.5 Tracking error
2.2 基于状态观测器的滑模控制
2.2.1 状态观测器的设计 在控制器(4)中,需要知道系统的所有状态变量,这在实际问题中是很难实现的,因为系统的状态变量大多数是未知的.为了解决这类问题,用设计状态观测器来估计系统中的状态变量x1、x2、x3,即根据状态变量的观测值来设计滑模控制器,达到控制效果.为了运算方便,在系统(1)中令

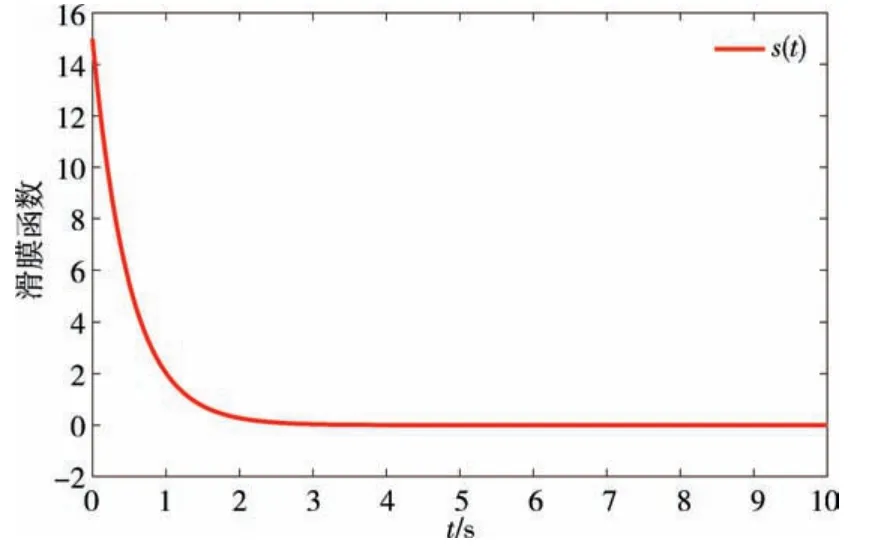
图3 滑模函数Fig.3 Sliding function
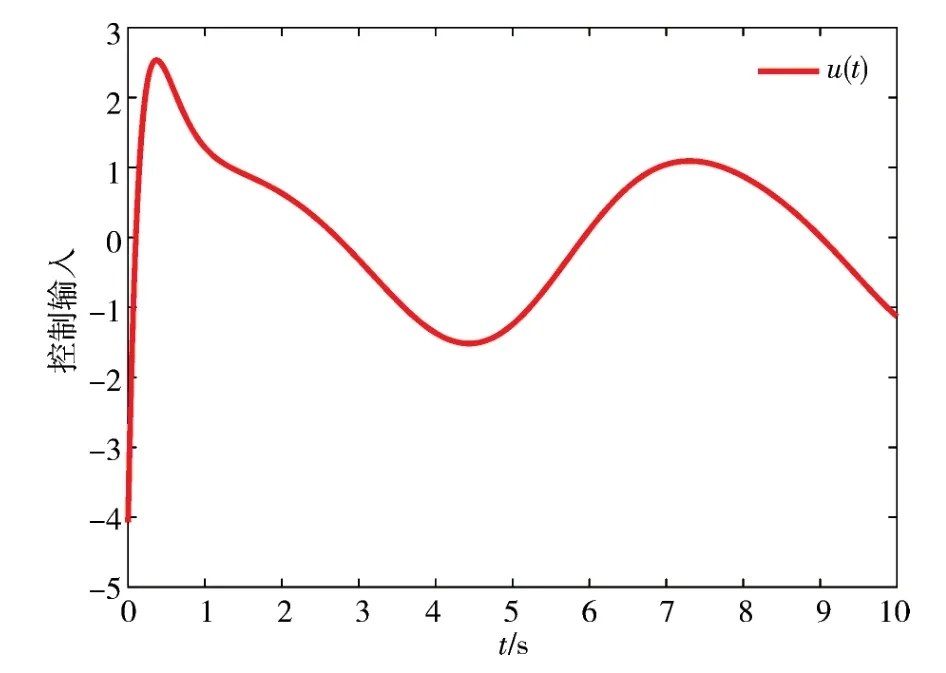
图4 控制输入Fig.4 Control input
则估计误差为
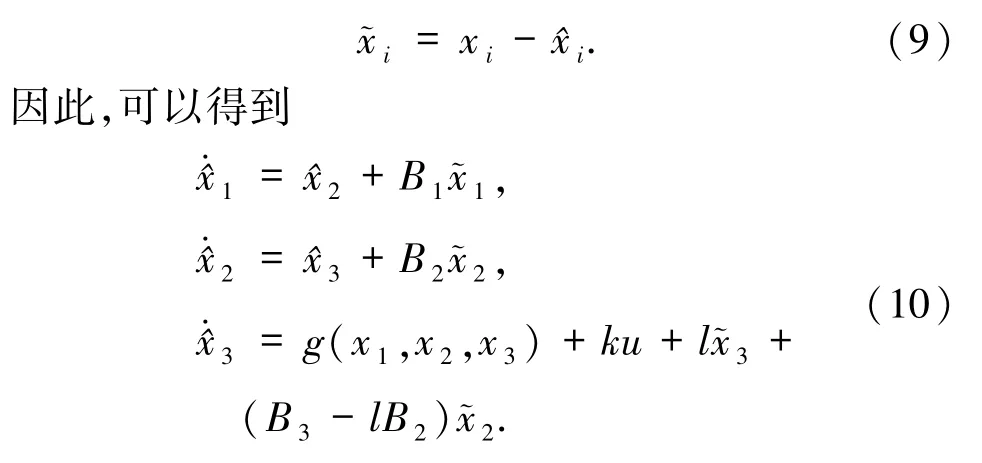
2.2.2 基于观测器的滑模控制设计
定理2对于系统(2),设计观测器(7)和状态变量估计值(8),则存在正常数k、ρ1和η,使得当t→∞时,观测器(7)是稳定的,观测误差~ei和追踪误差ei指数收敛于0,i=1,2,3.
证明下面分3部分来讨论.
1)设计观测器的稳定性.构造Lyapunov函数
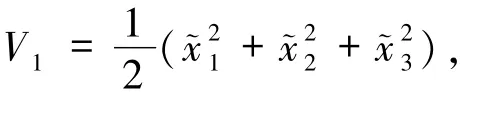
则
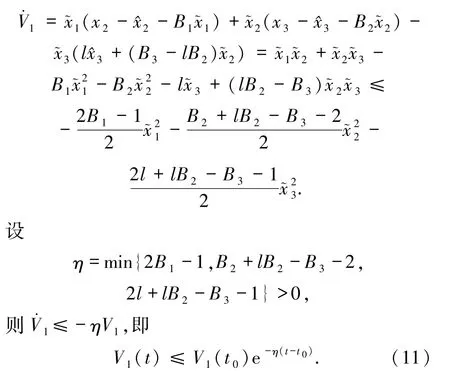
因此,设计的观测器(7)是指数收敛的.
2)观测误差是收敛的.假设控制目标为xd,定义追踪误差为


从而当t→∞时,V(t)指数收敛于0,从而追踪误差收敛于0,并且收敛速度由常数ρ1确定.
注2从(16)式中可以看到,滑模控制器的设计仅依赖于状态变量的估计值,而且能够使得追踪控制达到较好的效果,控制系统是指数稳定的,追踪误差趋于0.图6~图10给出了所设计的控制策略数值模拟图.通过比较可以看出,利用估计值所构造的控制器能够达到实际值一样的效果.
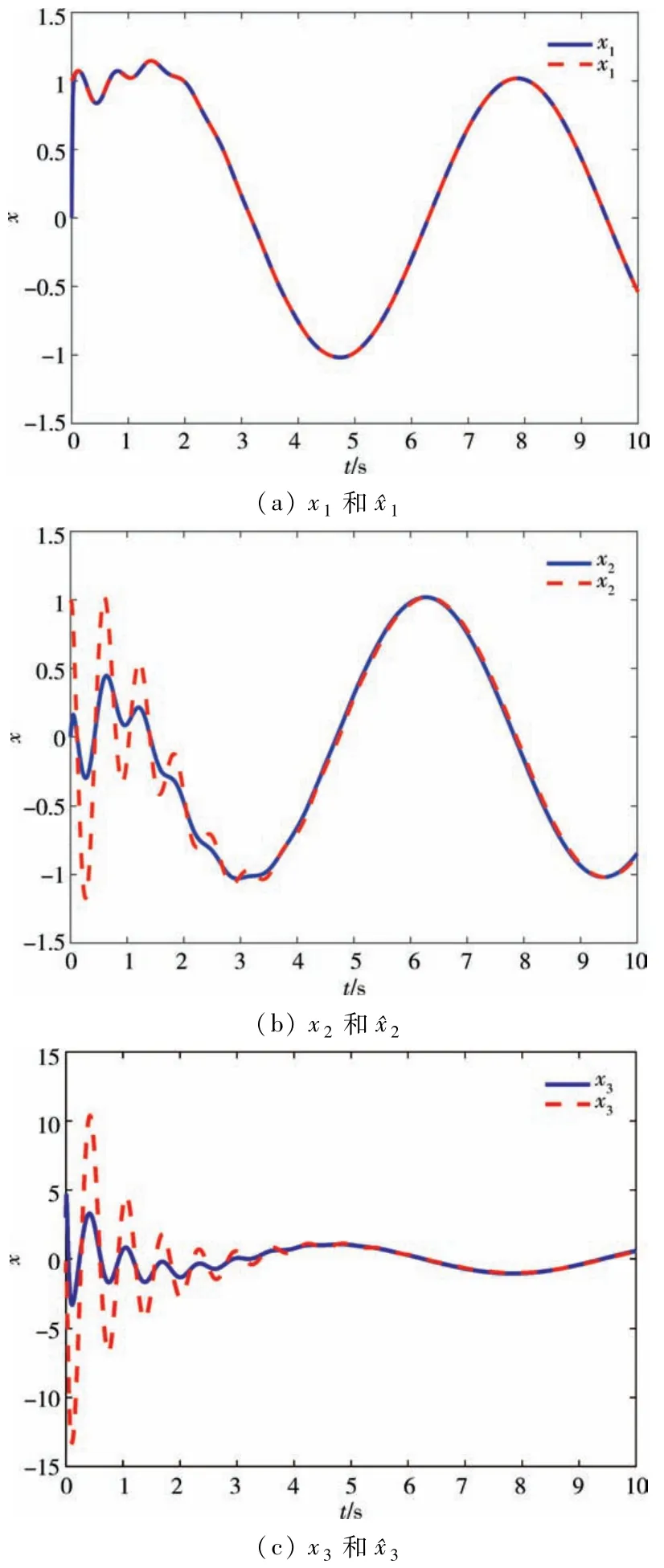
图6 状态变量估计Fig.6 The state variables estimation
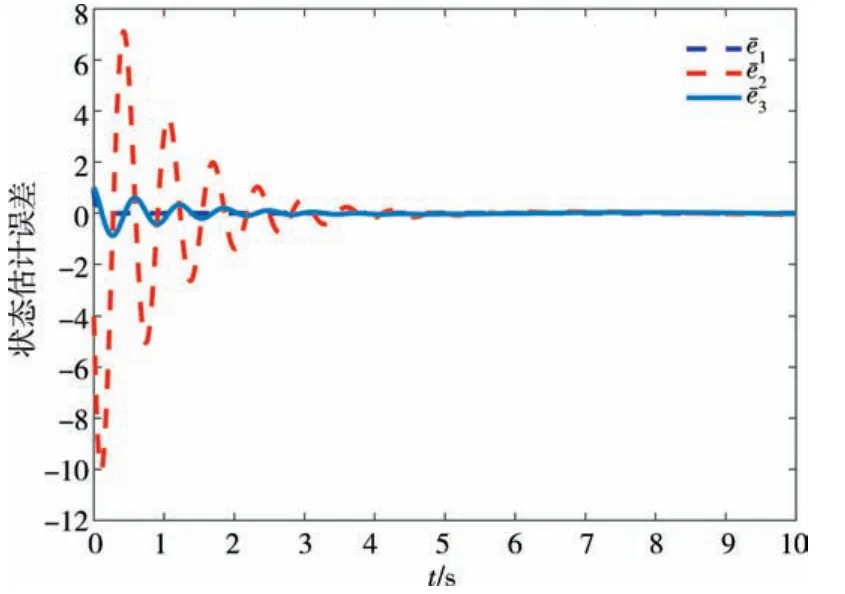
图10 状态估计误差Fig.10 The state estimation error
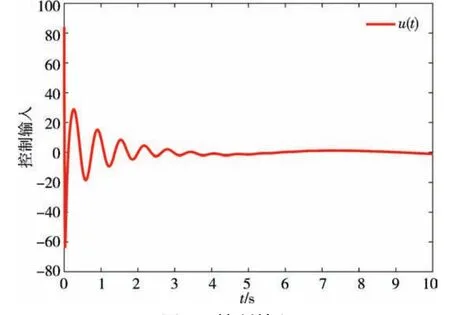
图7 控制输入Fig.7 The control input
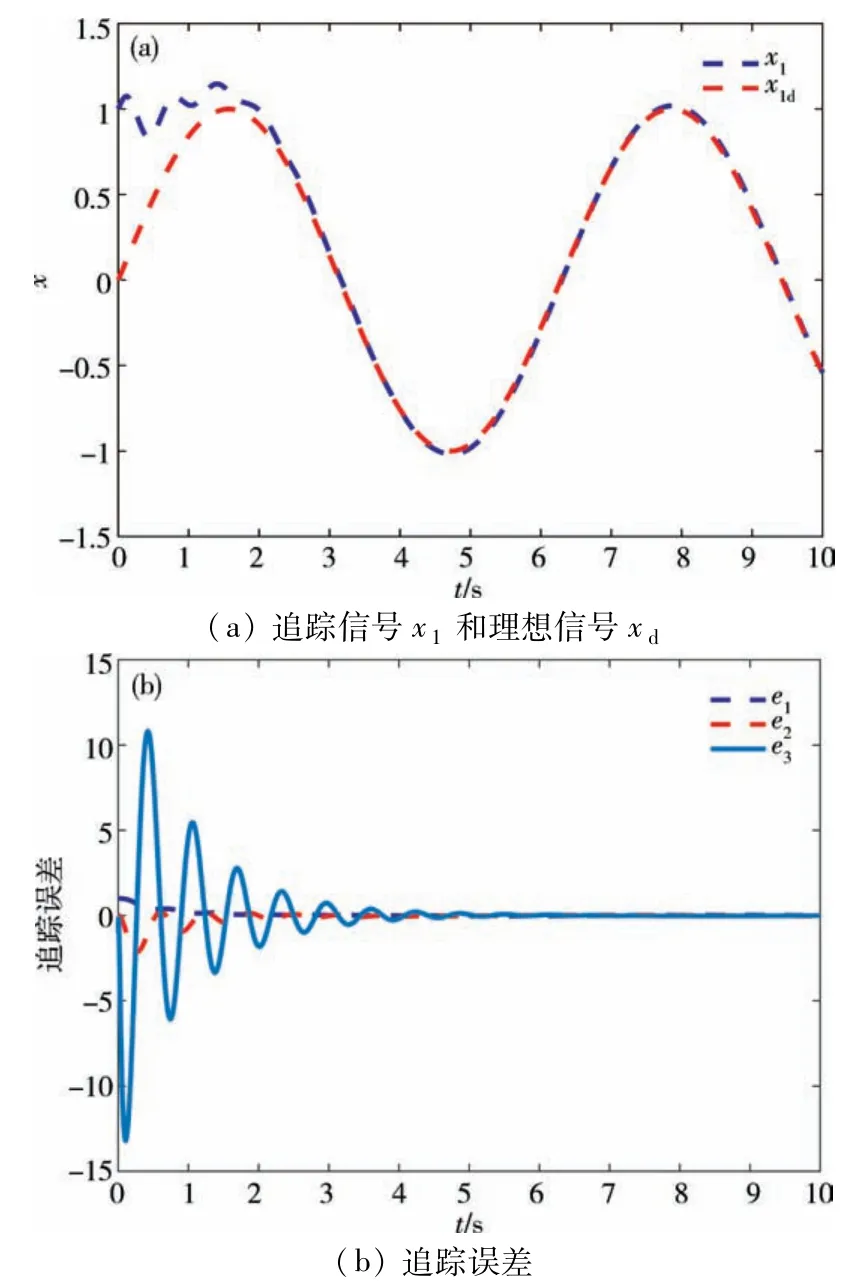
图8 追踪轨迹Fig.8 The trajectories of tracking
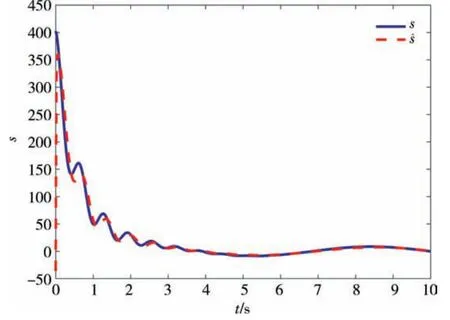
图9 滑模函数估计Fig.9 The estimation of sliding function
3 结论
为了获得混沌系统的轨迹跟踪控制,提出了一种基于状态观测器的自适应滑模控制方法.与传统的滑模控制设计不同,在研究的方法中,设计了观测器对状态变量进行估计,滑模面和控制器的构造仅依赖于估计值.实践证明,仍能达到传统滑模控制器的效果,能够保证状态变量跟踪所需的信号,追踪误差指数趋于0.
致谢淮南师范学院自然科学基金重点项目(2019XJZD09)和淮南师范学院微分代数系统的分析控制及应用创新团队项目(XJTD202008)给予了本文资助,谨致谢意.
