自承式给水钢管桥鞍式支座的计算方法探讨

雷晗 许大鹏

上海市政工程设计研究总院（集团）有限公司 200092

引言

给水钢管跨越河道、沟渠等障碍物时通常采用自承式钢管桥结构，其构造简单，受力明确，能避免水下施工，造价较低且维修方便，因此在我国南方地区得到了广泛应用。

自承式给水钢管桥的支座形式有很多，常用的基本形式有滑动式、滚动式和摆动式三类，其中滑动式支座又分为鞍式支座和环式支座两类。鞍式支座的包角为90°～180°，其结构形式简单，但与管道之间的摩擦力大，支承部位受力不均匀，一般用于直径不大于1m的钢管，鞍式支座的简图如图1所示。环式支座是在支座处的管身四周加刚性支承环，其摩擦力小，支承部位受力较均匀，一般用于直径不大于2m的钢管。在这几种支座形式中，鞍式支座的施工最为方便，因此在自承式给水钢管桥结构中得到了普遍应用，虽然相关文献中注明这种支座形式仅适用于直径不大于1m的钢管，但在目前已实施的工程案例中，采用鞍式支座的钢管桥最大管径已达到DN2200，远超相关文献建议值。且在实际工程应用中，根据现有规范理论公式计算得出的管道弯矩相比经验值往往偏大［1］，从而导致在设计中选用较大的钢管壁厚而造成工程浪费。

图1 鞍式支座简图Fig.1 Diagram of saddle support

本文对国内外鞍式支座的计算方法进行调研总结，并针对在实际工程应用广泛的新型支座形式给出理论计算公式，为钢管桥的结构设计优化提供参考。

1 国内相关研究

《自承式给水钢管跨越结构设计规程》（CECS214—2006）［2］（以下简称《规程》）中对于鞍式支座给出了支承处管壁环向最大弯矩可按下式计算：

式中：κ为鞍式支座处管壁的环向弯矩系数，各极点处的值见表1；R为支承宽度范围内的竖向反力（N）；r为钢管内半径（mm）。

表1 鞍式支座管壁环向弯矩系数κTab.1 Annular bending moment coefficient κ of pipe with saddle support

根据式（1），管壁环向弯矩最不利点为鞍式支座的边缘处。

该规程6.1.3条文说明中指出，内力计算公式及内力系数表均引自《压力钢管》［3］所提供的公式、附图、附表。

《压力钢管》［3］中指出，鞍式支座的优点是简单，但是其摩擦力较大，钢管与鞍座不易保证都完全为圆弧紧密贴合，在鞍座边缘处，钢管中也产生较大的弯矩，所以不适用于大型管道。该文献中采用图表的方式列出了常用鞍式支座管道的弯矩系数曲线。

《倒虹吸管》［4］中提到，地面明管在布置上，多为支墩或非连续支承，浅埋式暗管则为连续管座支承。支墩有鞍座式和滚动式及摆柱式几种形式，小型钢管多用鞍座式，包角一般为120°。在管壁与支墩接触点，焊有加强钢板，为保证钢管的轴向伸缩，在加强板与支墩间加有润滑剂。这种支座当管身产生轴向位移时摩擦力较大，钢管在支墩处承载能力有限，故只能用于直径不大于1m的钢管，支墩间距取5m～8m为宜。该文献中指出，管底支承反力的分布规律与管道铺设方式、管道刚度及地基土质有关，对于管底支承反力采用文克勒假定。

2 国外相关研究

日本的地下钢管实测资料反映［5］：将钢管铺设于90°凹圆的土基内，其管底支承反力呈抛物线分布规律。若在硬基上直接铺管，由于接触面极窄，管底反力会产生应力集中现象；如果采用包角为90°的混凝土管座，其最大应力将不出现在管顶或管底，而发生在管壳侧面，这说明不但基础形式对管壳应力产生影响，而且基础刚度也会对管壳应力发生作用。

美国土木工程师学会ASCE《Steel Penstocks》［6］中对鞍式支座进行了如下规定：鞍式支座一般用于管径和跨度较小（6m～8m）的情况，支承角度一般为120°～180°，角度越小，则管道应力越大，管道的应力分布如图2所示。规范中给出了管道环向最大弯矩点出现在鞍式支座的边缘处，其公式为：

图2 ASCE中鞍式支座的管道应力分布Fig.2 Annular stress of pipe with saddle support in ASCE

式中：Q为支座处的反力（N）；R为管道半径（m）；β＝π-θ/2，θ为支承角（°）。

美国水工协会《A guide for design and installation》（AWWA M11）［7］是输水钢管设计计算的主要参考依据，该指南中对鞍式支座未给出弯矩的计算公式，但是列出了管道在满水但无内压时鞍式支座处的最大应力公式如下：

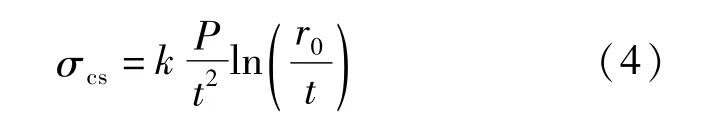
式中：k为支承角影响因子，k＝0.02-0.00012（β-90°）；β为支承角（°）；P为支座反力（N）；r0为管道半径（m）；t为管道壁厚（m）。

3 鞍式支座计算方法

3.1 边界条件推导

根据上述调研，国内对鞍式支座管道环向弯矩的理论计算源自《压力钢管》［3］，但该文献中并未注明相关计算假定及管道环向弯矩系数的理论公式。美国行业规范中给出了环向弯矩最大值的理论计算公式，但也未注明相关计算假定。而美国水工协会指南给出的公式则属于经验公式。

通过对比国内外的理论计算公式，可以发现它们之间具有很大的相关性：在支承角范围内，管道与鞍式支座完全贴合，管道环向弯矩为0。即可由此推断其边界条件假定为：在鞍式支座边缘处，管道与支座耦合，鞍式支座边缘为管道的固定支座。采用弹性中心法计算，管道环向弯矩系数κ的理论公式如下：

式中：β＝π-θ/2，θ为支承角（°）；α为距A点的角度（°）。

管道环向弯矩系数κ与支承角θ之间的相关曲线如图3所示，该图与《压力钢管》［3］及ASCE《Steel Penstocks》［6］均能吻合。

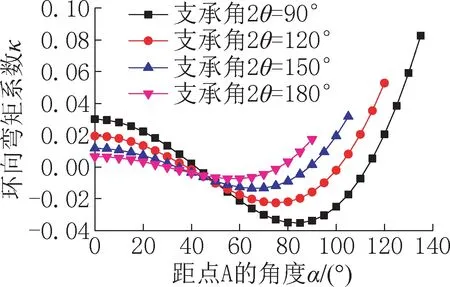
图3 鞍式支座的管道环向弯矩系数Fig.3 Annular bending moment coefficient of pipe with saddle support

要满足上述假定，管道需焊接固定在鞍式支座处，但焊接固定的支座形式不利于管道的检修和更换，且会破坏管道外防腐层，因此这与部分实际情况不符。

3.2 新型鞍式支座计算方法

随着鞍式支座构造形式的发展，华东地区目前已实施的数百座钢管桥中，其鞍式支座均采用钢管托或钢筋混凝土管托，如图4所示，在管道与支座之间设置不小于10mm的橡胶垫，该橡胶垫一方面保证管道与支座贴合，另一方面也对管道起保护作用，防止管道损伤。

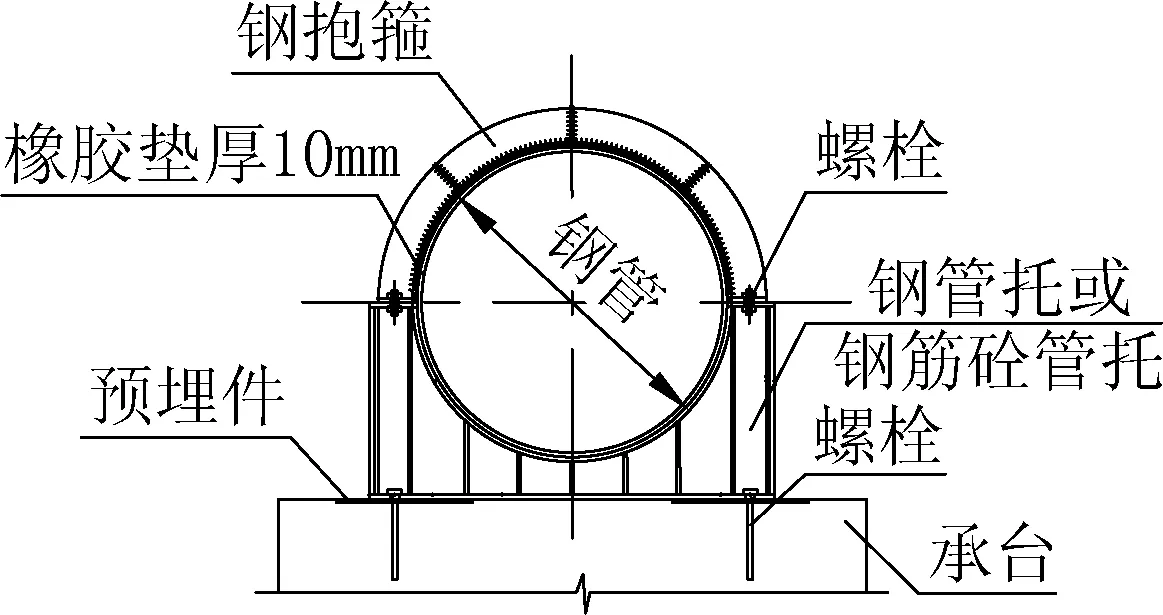
图4 华东地区鞍式支座构造Fig.4 Structural composition of saddle support in East China

《地下管道计算》［5］中提到，与管顶垂直压力与管侧水平压力一样，管底的支承反力及分布规律，对管截面应力及变位（柔性管）都影响较大。目前的管道设计中，对管底支撑反力的处理方法有：试验分析法、文克勒地基解析法、经验假定法以及弹性理论分析法等。对于位于土基上的柔性管，支承反力在接触面上按径向抛物线式分布，对于位于刚性管座上的柔性管，支承反力在接触面上按径向均布，如图5所示。

图5 管道支承反力分布（文克勒地基假定）Fig.5 Distribution of pipe reaction force（Winkler foundation assumption）

根据文克勒地基假定，采用这种鞍式支座的管道底部可视为刚性管座，支承反力可按径向均布计算，在橡胶垫的作用下，也可以进一步地将支承反力平均化。相应地，管道环向弯矩系数的理论计算公式如下：

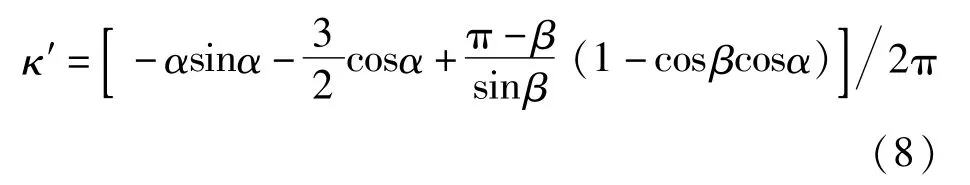
管道环向弯矩系数κ′与支承角θ之间的相关曲线如图6所示，随着支承角度的增大，管道环向弯矩系数逐渐变均匀。采用固定支座假定和采用反力径向均布假定的管道环向弯矩系数最大值对比见表2，在θ＝90°和θ＝150°时两者的数值基本相近，在θ＝120°和θ＝180°时后者比前者减小较多，尤其对于常用的180°支承角，最大环向弯矩系数减小至约83%，新型支座形式能较大地减小管道内力。

图6 鞍式支座的管道环向弯矩系数（反力径向均布）Fig.6 Annular bending moment coefficient of pipe with saddle support（radial uniform counter-force）

表2 鞍式支座管壁环向弯矩系数对比Tab.2 Comparison of annular bending moment coefficient of pipe with saddle support

4 结论

鞍式支座广泛应用于自承式给水钢管桥中，通过调研国内外相关研究，并与实际工程案例对比，可得出以下结论：

1.国内外的理论计算公式均假定鞍式支座边缘为管道的固定支座，在支承角范围内，管道与鞍式支座完全贴合，管道环向弯矩为0，即管道需焊接固定在鞍式支座处。

2.根据文克勒地基假定，对于底部设置钢管托或钢筋混凝土管托的管桥，管道与支座之间设置橡胶垫，管底支承反力在接触面上可视为按径向均布。

3.本文中给出了针对新型支座形式的管道环向弯矩系数的理论计算公式，对于常用的180°支承角，管道环向弯矩计算值能显著减小。