盲源分离不确定性问题研究综述

2021-11-15马艺伟黄小青

大连民族大学学报 2021年5期

肖瑛，马艺伟，黄小青

(大连民族大学信息与通信工程学院，辽宁大连116605)

BSS(Blind Signal Separation, BSS)[1]技术目前在语音信号处理、地震信号、故障检测等领域得到了广泛应用，近年来BSS的理论算法和工程应用得到了快速的发展，成为了信号处理的热点研究问题之一。BSS是仅仅根据观测到的混合信号来恢复出未知源信号的过程[2]。目前，在工程中，解决BSS运用极为广泛的算法有自适应算法[3-5]、非线性主分量分析法[6]、最大似然估计法[7-8]和贝叶斯独立元分析法[9]，上述方法，在大多情况下都能根据混合信号恢复出未知的源信号。

虽然BSS技术在工程上取得了较为成功的应用，但是目前已有BSS算法均存在一个技术瓶颈问题，即不确定性问题[10]。BSS对源信号进行估计时存在不确定性问题，就是估计信号的幅值任意比例的伸缩、先后顺序随意排序，在伸缩与排序的过程中，均保留了源信号的先验消息。因此，BSS不确定问题包括幅度不确定性和排列不确定性，针对此类问题，相关领域专家和学者展开了研究。

本文综合分析了目前已报道的研究成果，在介绍BSS混合模型的基础上，阐述了BSS不确定性问题产生的根源，并对其不确定性原因进行分类。针对BSS模型的幅度不确定性和顺序不确定问题，总结概括了已有算法的原理和优缺点。从具体算法示例的论述到整体分类，可以从宏观上更好的把握每种类别的算法在解决BSS不确定性问题的特点，为该问题的后续研究提出了新思路。

1 BSS不确定性问题研究现状

BSS问题的研究最早开始于1986年，Jutten和Herault[11]在美国举行的计算机神经网络会议上对BSS问题从数学方向上进行阐述，提出了基于神经网络结构的自适应算法，并成功解决了BSS问题，这一工作被公认为是BSS研究在国际上开始的标志，BSS研究的大幕也因此被拉开。

P.Smaragdis[12]在文章中介绍了运用短时傅立叶变换(Short Time Fourier Transform，STFT)的思想将信号卷积混合，代表BSS研究从时域研究转换到频域，利用独立分量分析(Independent Component Analysis，ICA)[13]技术，分离过程出现了不确定性问题，而使不属于同一源信号的频率段成分逆变换时，得到的分离信号仍然是混合信号，分离结果会产生一定影响。

到目前为止，解决幅度的不确定性问题，研究方法可以分为以下五类：分离矩阵法、源信号与分离信号差异法、压缩感知法、滤波器法和深度聚类法。在上述五类方法基础上，出现了很多典型的算法解决BSS幅度不确定性问题。顺序不确定性问题也分为以下四类：互参数法、耦合滤波器法、几何法和智能学习法。

总之，BSS不确定性问题的各类解决算法各有优缺点。BSS不确定性问题解决算法的研究，极大的拓宽了BSS的应用范围，推动了BSS技术在工程领域中的应用步伐。

2 BSS信号混合模型

2.1 根据源信号与观测信号数目分类

按照BSS模型中源信号与观测信号数目不同，可以分为超定型BSS(源信号数目小于观测信号数目)、正定型BSS(源信号数目等于观测信号数目)和欠定型BSS(源信号数目大于观测信号数目)。目前，在BSS领域以正定、超定BSS为主，正定和超定BSS算法研究较为成熟，应用范围最为广泛。而欠定BSS[14-16]不能直接采用正定和超定BSS算法来解决，对于欠定BSS问题，目前的通常做法有两种，一种是结合数据分解技术，将欠定BSS转化为正定BSS问题，在此基础上利用正定BSS算法实现分离；另外一种是利用信号的稀疏特征或者是信号变换域的稀疏特征，采用“两步法”[17-19]，即首先估计出混合矩阵，再进行源信号的分离。

2.2 信号混合方式分类

2.2.1 线性瞬时混合

线性瞬时模型是最简单的BSS模型，也是目前研究最为成熟的一种模型。通常ICA技术，使得输出分量间相互独立。即确定采取一种判断依据作为混合信号接近相互独立的准则，采用BSS算法来达到相互独立目的。设源信号为S(t)=[s1(t),s2(t)…,sn(t)]T，观测信号为X(t)=[x1(t),x2(t),…,xm(t)]T，A是m×n的未知混合矩阵，t是离散时间变量。当A是非奇异且时不变的矩阵，此时的混合模型为瞬时混合。那么瞬时混合模型可表示为

X(t)=AS(t)。

(1)

如果m=n，则式(1)中给出的混合模型的BSS模型称为正定分离问题，此时，约束混合矩阵A满足非奇异且时不变，即分离矩阵A满秩可逆，则一定可以得到一个逆矩阵使得式(2)成立。

Y(t)=WAS(t)。

(2)

W、A趋近于单位阵。若可以使W、A分解为WA=PD形式，其中P是一个正交矩阵，D是对角矩阵，则说明源信号可分离，即

Y(t)=WX(t)=PDS(t)。

(3)

而对于正交矩阵P和对角矩阵D，对角矩阵D的系数决定了幅度的不确定性，正交矩阵P的排列造成了顺序的不确定性。BSS原理图如图1。

图1 BSS原理图

2.2.2 线性卷积混合

线性卷积模型的BSS算法是目前BSS领域研究的热点。源信号通过一个特定系统，做时域卷积处理，获得卷积模型。卷积模型比较于瞬时模型复杂很多，假设(1)式的非奇异且时不变的矩阵A用滤波器矩阵代替，混合方式为卷积混合。在t时刻有n个源信号为S(t)=[s1(t),s2(t)…,sn(t)]T，卷积混合后被M个接收机接收，观测信号为X(t)=[x1(t),x2(t)…,xm(t)]T，针对正定、超定模型分离进行研究，则第i个传感器接收到的信号xi(t)可以表示为

(4)

式中：xi(t)为第i个传感器的输出信号；sj(t)为第j个源信号；P为aij滤波器的阶数；aij表示第j个源信号与第i个传感器的滤波器的第P个系数；*表示卷积。这一卷积混合过程可用向量表示为

(5)

其中，

(6)

卷积混合BSS的目标就是求得一个Q阶n×m的分离滤波器矩阵W(q)，使得

(7)

同理，对角矩阵D的系数决定了BSS幅度的不确定性，置换矩阵P的排列造成了BSS顺序的不确定性。

2.2.3 非线性混合

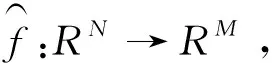
非线性混合分为一般非线性混合和后非线性混叠混合(PNL)。非线性BSS研究主要有两类方法：基于自组织映射(SOFM)直接提取非线性分量的研究；基于非线性混合模型的研究，学者较多关注第二类方法。非线性混合模型的建立有三种方法：后非线性混合模型(PNL)；Mono非线性混合模型。LNL层叠模型。PNL模型[20]结构简单，容易分析，是目前常用的非线性混合模型。一般非线性混合模型为

x(t)=f(s(t))。

(8)

后非线性混合是先进行线性混合，再进行非线性混合，而PNL混合模型具有很强的实际意义。混合过程为

x(t)=As(t)，

(9)

z(t)=f(z)=f(As(t)) 。

(10)

式中：X是线性混合后的信号；Z是非线性混合后的信号；其他参数均未知。PNL混叠、分离模型如图2和图3。

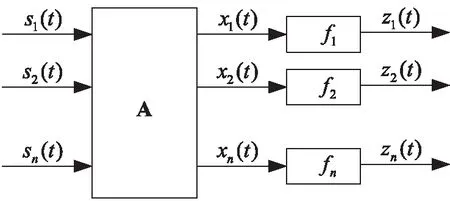
图2 PNL混叠模型

图3 PNL分离模型

PNL模型的BSS过程为

u=g(x)，

(11)

y=Wu=Wg(x)=Wg[f(As)] 。

(12)

2.3 信号混合通道分类

BSS技术根据混合通道个数可分为单通道[21-23]和多通道[24-25]信号分离。单通道BSS是从n维未知混合源信号只获得一路观测信号，从这一路混合信号中分离出n维源信号。多通道信号BSS是n维未知混合源信号混合获得m维观测信号，从这m维混合信号中恢复出n维源信号。

3 解决BSS幅度不确定性问题的方法

针对幅度不确定性问题总结以下五类方法：即分离矩阵法，源信号与分离信号差异法，压缩感知法，滤波器法和深度聚类法，五类方法均可一定程度的消除幅度不确定性问题。

分离矩阵法由文献[26]提出，该法应用于线性瞬时混合模型，是以单位阵为标准，强制每个频率段分离信号以单位幅度为标准进行统一的伸缩，从而消除每个频率段上的幅度不确定性。具体操作分别将每个频率段上求得的分离矩阵做归一化处理。设某一频段上分离矩阵为W(f)，则最优分离矩阵为Wopt(f)=W(f)/W(f)。分离矩阵归一化法在操作上简洁，程序编写很容易实现。不过，分离矩阵归一化法具有一定的局限性，经过分离矩阵归一化处理的分离信号在中频段和高频段与源信号比较相近，在低频段与源信号有些偏差，经过分离矩阵归一化处理的信号波形虽然在幅值与源信号不一致，但在波形上与源信号大体相同，说明分离矩阵归一化法可以在一定程度上消除幅度不确定性问题。

2.艺术范畴的毛笔书法作品。关于毛笔书法作品与艺术之间的关系是不用赘言的。古今名人字画皆是书画爱好者的赏析和收藏的宠儿，也是研究和发展东方艺术的不竭源泉。所谓艺术，即是人类在漫长的生产活动和社会活动中形成和创造的成果，是人们为了满足自身的需求，以一定的物质载体为中介，以丰富的情感来表现社会生活和审美情趣的审美形态。美术作品即是艺术的一种表现形式。而美术作品，是指绘画、书法、雕塑等以线条、色彩或者其他方式构成的平面或者立体的造型艺术作品。毛笔书法作为书法门类中一种独特的表现形式，当然属于美术作品。因此，从艺术范畴的角度来看，毛笔书法作品应该受到著作权法的保护是毋庸置疑的。

最小失真法[27]传统BSS混合模型，在信号分离过程中，主对角线上的元素导致了幅度不确定性，而解决方法是使分离信号y(t)与源信号x(t)之间均值相差最小，表示为E{y(t)-x(t)2}最小。若可以满足最小失真条件，分离矩阵被视为最优分离矩阵。最小失真法的源信号经BSS后以幅值为标准，限制每个频率段上的幅值都最大限度的贴近这个标准。最小失真法适用于低频段、中频段、高频段的信号，经处理后的分离信号与源信号幅值非常相近，基本与源信号保持一致，确保了算法的有效性。但是，要确保源信号的先验信息，保证源信号的稀疏特性，应用的范围又具有局限性。

压缩感知法[28]是基于压缩感知模型对原始信号稀疏性要求，和盲源分离模型中的系数成分分析方法的相似性，对信号进行处理，去除信号之间的差异，把信号BSS问题转化压缩感知理论解决信号的重构问题，最后将重构信号依靠传统的自适应归一化去除信号的幅度不确定性。该类方法通过K聚类算法估计混合矩阵，使其变化为满足压缩感知理论的形式；依据估计出的混合矩阵并结合自适应步长迭代算法，重构源信号，实现幅度的矫正。稀疏信号重构中的贪婪算法[29]在源信号充分稀疏的情况下表现出更好的性能，并且由于其具有更低的时间复杂度，近年来受到了广泛重视。但是，此类方法存在的主要问题是对于源信号的稀疏性和数据采样点数要求极高，且计算时间较长计算量过大。

滤波器原理对BSS幅度不确定性问题进行校正，分析概括五种校正方法。文献[30]维纳滤波器是经典的线性BSS滤波器。针对传统BSS模型，设计滤波器的参数使滤波器输出端以均方误差最小恢复源信号，使分离信号无线逼近与源信号。在均方误差最小的最优准则下，维纳滤波是一种最优滤波器。文献[31]针对维纳滤波原理进行改进，提出小波滤波原理BSS幅度性矫正。小波滤波将估计信号分为两个分量，即幅度分量和偏移分量，对分离信号的幅度分量进行限制使其近似于源信号的幅度分量，并且小波滤波在高频范围内具有较高时间分辨率，在低频范围内具有较高频率分辨率，确保算法的性能。文献[32]提出粒子滤波原理幅度性矫正。其基本思想是对未知信号的后验概率分布进行蒙特卡罗采样，调整每路分离信号的权重，逼近最终源信号的概率分布函数。将每路输入信号称为看作一个粒子，将每个粒子都作采样处理，对采样的粒子权值更新，完成权值归一化，消除幅度不确定性。文献[33]针对非线性混合信号实现幅度性矫正。线性共轭线性频移滤波器(Linear-Conjugate-Linear Frequency Shift Filter，LCL-FRESH)又称为LCL-FRESH滤波器，其原理是对混合信号做循环谱估计，得到其具有最强谱相关特性的循环频率点，便可确定LCL-FRESH滤波器频移操作部分的频移量。通过归一化LMS算法使得均方值达到最小，得到最优的滤波器参数，实现幅度矫正。文献[34]是基于组合滤波器进行幅度性矫正。该方法针对卷积BSS模型，用形态学运算子对输出信号组合处理，根据目标稳定特性设计频域波器，输出结果做卷积处理，完成分离信号的归一化，在保留源信号先验信息的条件下最大程度的估计源信号。几种常见滤波器幅度性矫正方法的性能比较见表1。

表1 滤波器幅度矫正方法的性能比较

深度聚类算法(Deep Clustering，DC)[35]主要思想是将一个低维度的信号幅值谱特征，映射到一个更高维度的深度嵌入式特征空间中，即对每一个时频单元映射成一个D维的特征向量。这样，将二维特征映射到三维空间使得输入的混合特征更加具有区分性。最后，利用K-means聚类算法对该嵌入式向量进行聚类，得到估计的解混矩阵。其中映射过程是利用深度神经网络实现的，利用最小均方误差准则对源信号恢复。但目标损失函数是在嵌入式向量上，而不是真正的目标信号的幅值谱，最主要的是该嵌入式向量跟源信号存在一定的误差，分离效果不好。基于深度嵌入式特征和区分性学习的分离算法(DEF-DL)[36]。该方法主要是将DC看成一个特征提取器，利用DC算法提取一个具有区分性的深度嵌入式特征，将每个时频单元映射到一个更高维度的向量空间，获取深度嵌入式向量，利用无监督的K-means聚类算法就可以将混合信号分离出来，该深度嵌入式向量是一个具有区分性的混合信号分离特征。为了使得目标函数可以直接定义在真实的目标幅值谱上，DEF-DL利用有监督的网络替换掉了K-means聚类算法。即将该深度嵌入式特征作为PIT网络的输入特征，将源信号分离出来，对分离信号归一化处理，不仅解决幅度不确定性也实现顺序不确定性矫正。该算法很好的解决了DC的缺点，同时将DC和PIT算法深度的融合起来，取得了不错了分离效果。

分析认为，解决幅度不确定性问题的研究方法即分离矩阵法、源信号与分离信号差异法适合于线性混合的平稳信号，压缩感知法对源信号稀疏性要求极高，滤波器法和深度聚类法适应于大多BSS模型，并且深度学习法已成为当今的主流趋势。

4 解决BSS顺序不确定性问题的方法

针对解决顺序不确定性问题总结以下四类方法：即互参数法，耦合滤波器法，几何法和智能学习法，四类方法均可一定程度的消除顺序不确定性问题。

表2 互参数法顺序矫正方法的性能比较

耦合滤波器法通过限制窗长度和分离滤波器的长度来保证其在时频域上的平滑性以达到更好的分离效果，当不同频率段上的分离矩阵顺序不一致的时会导致分离滤波器变长，这样可以通过限制分离滤波器的长度来消除信号输出顺序不确定问题。文献[41]，耦合滤波器法的算法思想是在时频域进行的BSS与滤波器相结合，调整滤波器的参数使滤波器形成最优滤波器系统，在此系统上通过限制窗的长度及分离滤波器的长度可以保证其平滑性达到更好的分离效果。该方法提出时间较早，算法相对成熟，但是此类算法的解决效果不是最佳。

几何法是指通过波束形成，传感器之间的几何信息等解决顺序不确定问题。特殊场景下的BSS问题中，利用目标信号的先验信息进行信号分离。具体来说，通过目标信号的相关性知识对原有算法的目标函数进行约束，可以实现对解混矩阵与特定未知源信号的估计。文献[42]针对常规场景下的DOA估计，DOA估计方法是在每个频点上估计源信号的波达方向，并以此为特征对各个频点上的独立分量进行聚类，确定每个独立分量对应的源信号。分析分离矩阵形成的方向性图案，估计源信号方向，重新排列分离信号，解决顺序不确定问题。文献[43]，针对干扰信号的DOA估计，在干扰信号和目标信号方向未知的情况下，利用干扰信号与目标信号的大功率差特性，估计干扰信号的来波方向，利用斜投影在干扰信号的零空间上估计目标信号的来波方向，如此反复迭代，依次估计干扰信号和目标信号的来波方向，最终得到目标信号DOA估计，重新排列估计信号，解决顺序不确定性问题。DOA估计一直以来是空间谱估计问题中的一个重要方向，日益复杂的电磁信号环境以及特殊的问题场景使得传统算法无法达到估计精度要求。针对场景特殊性研究合适的算法，是现在广大学者研究的重点。不过DOA估计法存在一些缺点，该算法在某些方向无法准确估计到达的方向频率，其在低频下，由传感器间距引起的相位差非常小；在高频下，可能会发生空间混叠；并且通过绘制方向性图来计算方向很费时，无法保证实验的准确性。

智能学习法是指利用耦合隐马尔科夫模型(Coupled Hidden Markov Model，CHMM)，分派问题(Assignment Problem，AP)和动态规划(Dynamic Programming，DP)等解决顺序不确定性问题。文献[44]，智能学习算法是指将CHMM，AP和DP进行结合，即将两个相邻的两个信号视为“分派问题”中的源节点和目标节点。而该算法的目的是使节点之间的成本总和最小化，实现“动态规划”。最后使用CHMN解决顺序不确定性问题。考虑到在某些情况下需要从全局信息来获得匹配，因此将使用CHMN和DP结合在一起，才可实现排列顺序的矫正。该算法的主要问题是：在估计模型参数的时候易收敛到局部极值点，算法对模型中参数的初始值依赖性较大。

分析认为，解决顺序不确定性的研究方法即互参数法为当下主流算法，引发众学者的关注，耦合滤波器法提出较早，分离性能无法保证，几何法和智能学习法涉及的工程应用范围不广泛。

5 BSS不确定性问题研究展望

BSS问题自上世纪末期以来，在理论和研究方面都获得了发展。但是，针对BSS的不确定性问题的研究，并未有完整的知识体系完全解决此类问题。学者们逐渐认识到，针对BSS的不确定性问题，应该对算法提出不同的要求，例如算法的鲁棒性、稳定性、实时性和精确性等，使BSS算法的研究有针对性。分析认为，针对BSS不确定性问题研究方面，面临以下问题亟待解决。

(1)在时域中解决BSS不确定性问题，应用的算法相对较少，没有针对性的说明此类算法的可行性。

(2)针对不同的BSS模型，不确定性问题的算法并未针对性的解决相对模型问题，没有完全适应于任何系统的算法，成功解决该类问题。

(3)解决BSS问题目前主要基于源信号的稀疏性，尽管源信号非充分稀疏在一定条件下也可以分离，但是其分离效果会降低，特别是随着源信号个数的增多，信号分离精度会下降，因此如何提高信号的稀疏度还需进一步研究。

(4)BSS的顺序不确定性问题的算法吸引学者的关注，但是应用范围并不广泛，应建立鲁棒性更好、适应性更强的分离模型，提高算法的有效性。

(5)解决了BSS不确定性问题，对生活中的实际应用研究较少，应拓宽其实际应用，解决工程问题。