自由面变化条件下隧道电子雷管爆破参数确定方法*

刘翔宇，龚 敏，吴昊骏，安 迪

（北京科技大学土木与资源工程学院，北京 100083）

电子雷管的应用是爆破技术的重大进步[1-2]。与普通雷管相比，电子雷管延时精度提高10 倍以上，起爆段别成百倍增加[3-4]，在提高爆破效果特别是在降低爆破振动[5]、控制爆破损伤[6]方面具有广阔前景。2009 年我国在隧道中首次采用了电子雷管起爆技术[7]，近年该技术已大量应用于隧道工程，均取得很好的效果。

从目前来看，国内隧道爆破中电子雷管的应用潜力并没有得到充分发挥，一个重要原因是还没有一套系统、有严密理论支撑的电子雷管爆破参数计算方法。隧道爆破的关键参数是炮孔药量和孔间延时，当前对有振动控制要求的隧道爆破采用常规方法设计参数，以误差较大的萨氏公式计算药量[8]；延时参数则由一些学者[9-12]多次实验总结得出并被大多数工程采用；田振农等[13]提出将相邻波形半周期倍数作为孔间延时，利用波形错峰干扰降振，鉴于爆破振动波不是周期波，是否适用所有情况仍有待验证。

近年流行的Anderson 振动合成理论[14-16]为安全振速下准确设计爆破参数带来希望。龚敏等[17]、吴昊骏等[18]基于普通导爆管雷管，测试每段样本雷管延时范围，计算延时范围内所有可能的叠加合成振速，并以最不利情况设计药量，能大致确定第二自由面形成前的掏槽参数；Iwano 等[19]采用电子雷管起爆，通过叠加计算准确获得了最佳延时。目前未解决的难题是隧道一次微差爆破的各种功能孔上百个，药量和位置各不相同，振动合成计算时难以界定不同功能炮孔的数目和药量差异；尤其是不能根据自由面变化相应地调整药量和延时参数，无法在低振速下以最大药量实施精准、高效爆破。

本文中，以重庆观音桥隧道为研究背景，利用电子雷管起爆时间准确的特性，基于安全振速提出在单自由面形成双自由面过程中，不同自由面条件下电子雷管爆破参数设计方法。获取现场不同自由面单孔爆破波形作为计算振源；通过比较计算振动曲线与实测振动曲线判断第二自由面形成时间；利用Anderson 理论和计算程序进行延时振动合成计算，得到各类炮孔延时、药量与振速之间的量化关系，准确确定爆破新自由面形成前、后的药量和延时参数。本方法在低振速控制的同时实现高效进尺，有利于发挥电子雷管延时精确的优势。

1 研究原理与实现方法

1.1 基本方法

主要研究隧道爆破关键参数炮孔药量、孔间延时的确定方法（其他参数可据此得到）。延时爆破合成振速是确定隧道爆破关键参数的依据，本文中基于Anderson 理论进行电子雷管爆破振动合成计算，即在隧道工作面进行单孔爆破试验，基于测得的单孔振动数据计算不同延时的爆破合成振速。

考虑到隧道爆破从单自由面到双自由面的变化对爆破效果影响巨大，故针对不同自由面采用不同的参数计算方法。以现场不同自由面单孔爆破振动数据分别计算相应的延时合成振速，对计算结果分析后确定安全振速下不同爆破时段的药量、延时等爆破参数。图1 为研究思路的流程图，具体步骤为：现场试验获取单自由面单孔爆破振动数据，计算不同药量、延时的爆破合成振速；基于电子雷管设计短延时掏槽爆破试验，确定隧道爆破的第二自由面形成时间；根据形成时间设计双自由面下单孔爆破试验，再计算第二自由面形成后的延时振动合成曲线。按上述方法，计算药量变化时延时爆破振动合成曲线组合，最终确定安全振速下最优爆破参数。

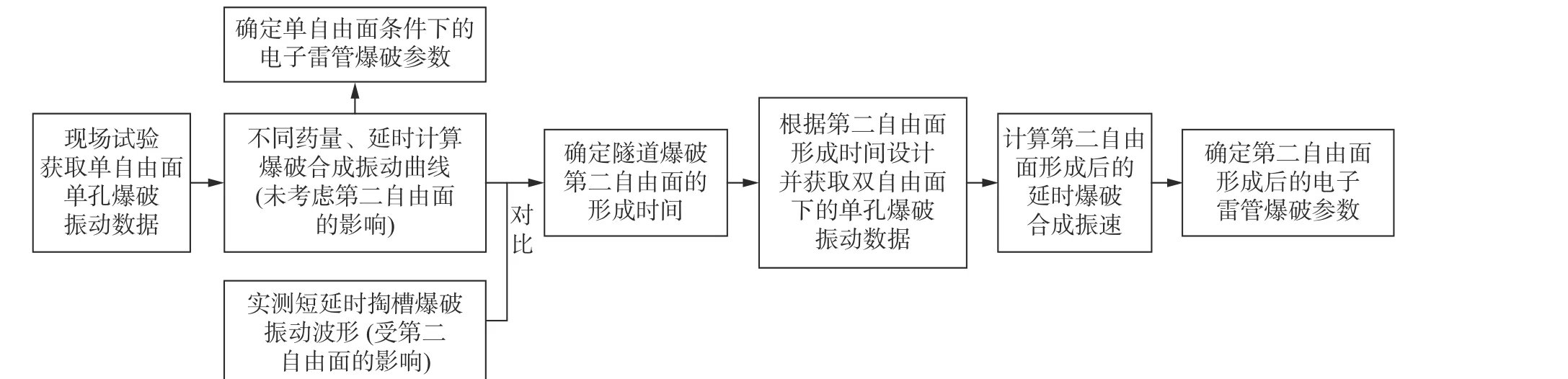
图1 研究流程Fig. 1 Research process chart

1.2 现场单自由面单孔爆破试验与振动曲线拟合

在隧道工作面进行单自由面下不同药量的单孔爆破试验，并测试爆破振动数据，采用Fourier 级数的三角函数形式，利用MATLAB 编程得到单孔波形的拟合函数f(t)：

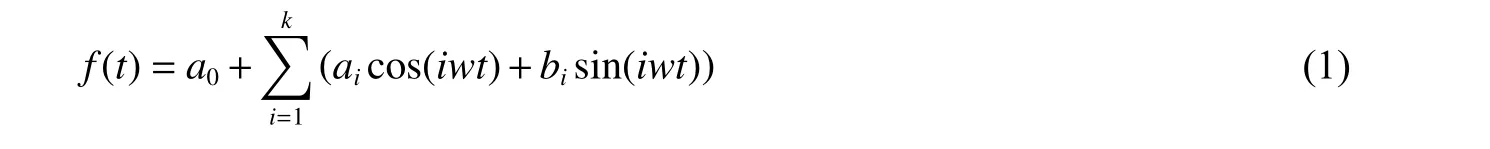
式中：t为时间，a0、ai、bi为Fourier 拟合系数，ω 为基频，k为Fourier 拟合级数。

Fourier 拟合系数a0、ai、bi及基频ω 的计算公式如下：

式中：M为总采样点数，ym为第m个采样值，T为波形截断时间。

将拟合函数f(t)扩展至时间全域，得到单孔波形函数公式v(t)：

为区别后续第二自由面形成后的单孔波形函数，将单自由面单孔波形函数记为v1(t)，第二自由面形成后单孔波形函数记为v2(t)。

1.3 延时爆破振动合成计算方法

由于同类型炮孔药量相同、炮孔间距相比爆源至地表测点距离可忽略，可认为N个同类孔的单孔振动波形相同。以掏槽孔为例，按照不同孔间延时Δt对v1(t)进行N个炮孔的线性叠加计算，得到延时合成波形函数：

式中：v(t,Δtn)为掏槽孔叠加合成波形函数，v1(t)为单自由面下单孔波形函数，Δt为选择的相邻孔间延时（各相邻孔间延时取相同值），Δtn为第n个掏槽孔的起爆时间。

1.4 单自由面下爆破参数的确定

1.4.1 孔间延时Δt变化时延时爆破最大合成振速的计算

当Δt=1 ms 时，叠加合成波形函数v(t,(0,1,2,···)) 存在最大振速vmax(t,(0,1,2,···)) ，Δt=2 ms 时，叠加合成波形函数v(t,(0,2,4,···)) 存在最大振速vmax(t,(0,2,4,···)) 。所有孔间延时下叠加合成波形函数的最大振速组成了集合 {vmax(t,(0,Δt,2Δt,···))} ，在集合中找出最小值，即：

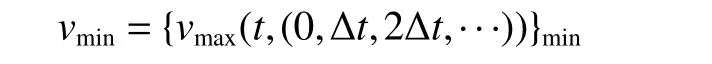
式中：vmin为所有孔间延时下叠加合成最大振速中的最小值，Δt为孔间延时，vmax(t,(0,Δt,2Δt,···)) 为某孔间延时Δt下叠加合成波形的最大振速。

1.4.2 确定优化药量和孔间延时参数

考察符合安全振速标准vstan的可能单孔装药量 {Q1,Q2,···,Qj} ，寻找可能药量中满足安全振速的最大药量，实现循环进尺的最大化。

对于任意单孔装药量Qj，通过1.4.1 节的运算，都将得到vmin,j，找出 {vmin,1,vmin,2,···,vmin,j} 中所有小于vstan的值，记为 {vsafe,1,vsafe,2,···} ，对应的单孔装药量记为 {Qsafe,1,Qsafe,2,···} ，在集合 {Qsafe,1,Qsafe,2,···} 中找到药量最大值Qmax，即为安全振速下的最大单孔装药量。对比Qmax药量下不同孔间延时的叠加合成振速和vstan，选择合成振速最小的孔间延时作为设计参数。

以上为单自由面爆破参数，也必定是最先起爆的掏槽爆破参数；但在逐孔掏槽中是部分时段或全过程为单自由面还需要进一步研究，在得到第二自由面形成时间后，再确定形成后的爆破参数。

1.5 确定第二自由面形成时间

如何利用隧道爆破形成双自由面后的降振作用是研究中需解决的问题，其关键是要获取第二自由面形成的确切时间。本文方法是：1.3 节计算合成振动曲线没有考虑第二自由面的形成对振速的影响；而现场实测得到的是包含第二自由面降振作用的爆破振动曲线；将两种曲线在同一图上比较，参照文献[20]中第二自由面形成时间的判据，相同时刻两曲线振速显著差异（2 倍以上）的起始点即为第二自由面形成时间Tsf。

1.6 第二自由面形成后爆破振动合成计算与爆破参数确定

1.6.1 第二自由面形成后单孔爆破试验

第二自由面形成后计算延时爆破合成振速的前提是获得双自由面下的单孔爆破振动波形，由于既有双自由面下单孔波形与从单自由面向双自由面动态转化过程中的单孔波形差异较大，为准确计算第二自由面形成动态过程的爆破振动合成，需先用1.5 节方法获取第二自由面形成时间，再据此设计第二自由面形成后动态时段的单孔爆破试验，详见后面计算应用实例。

1.6.2 主掏槽与辅助掏槽孔间延时的确定方法

当前设计隧道爆破参数时通常在不同类型炮孔，如主掏槽最后起爆孔与辅助掏槽首爆孔之间设置长时差以确保第二自由面作用[9]，这个长时差依靠经验设计，一般在20～70 ms 间取值。本文尝试用理论分析方法确定时差参数。

为使取值范围有代表性，主掏槽最后起爆孔与辅助掏槽首爆孔的孔间延时ΔD按5～50 ms 计算延时爆破合成振速变化值。按照ΔD取值和第二自由面形成时间Tsf，分3 类情况进行计算，计算公式如下：

（1）当(N1-1)Δt1＜Tsf，(N1-1)Δt1+ΔD≥Tsf时，即主掏槽最后孔起爆时未形成第二自由面，辅助掏槽首爆孔起爆时已形成第二自由面：

式中：v(t,ΔD)为合成波形函数，v1(t)为单自由面单孔波形函数，v2(t)为第二自由面形成后单孔波形函数，N1为掏槽孔个数，N2为辅助掏槽孔个数，n1表示从0～(N1-1)的数值，n2表示从0～(N2-1)的数值， Δt1为主掏槽相邻孔孔间延时，Δt2为辅助掏槽相邻孔孔间延时，ΔD为掏槽最后起爆孔和辅助掏槽首爆孔的延时间隔5～50 ms，Tsf为第二自由面形成时间。

（2）当(N1-1)Δt1≥Tsf时，即主掏槽最后孔起爆前已形成第二自由面：

式中：k1为第k1个掏槽孔（该孔起爆时形成第二自由面)。

（3）当(N1-1)Δt1+ΔD＜Tsf时，辅助掏槽首爆孔起爆时未形成第二自由面：

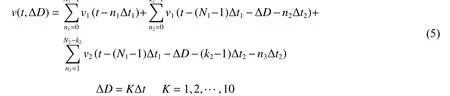
式中：k2为第k2个辅助掏槽孔(该孔起爆时形成第二自由面)。

1.6.3 辅助孔孔间延时与单孔药量的确定

辅助孔单孔药量可按掏槽孔减少（15～20）%选取，对第二自由面形成后单孔波形进行拟合，得到单孔波形函数v2(t)，根据v2(t)的叠加计算获得孔间延时参数。

2 应用案例

重庆市观音桥商圈北大道隧道位于重庆市中心区域，施工区有密集地面建筑物及地下管线，需严格控制爆破振动，要求地面振速不超过1.0 cm/s。试验段采用电子雷管逐孔延时爆破（电子雷管精度±1 ms）、全断面一次爆破成形。

爆破试验在隧道左洞K1+330～K1+367 区段进行，隧道断面11.8 m×9.55 m，面积90.85 m2。隧道属浅埋隧道，埋深20～30 m。隧道围岩主要为砂岩，无不良地质现象，围岩类别为Ⅳ级。

2.1 现场单自由面单孔爆破试验

为提高现场试验效率，每次试验爆破两孔，图2 为炮孔布置图。孔1、孔2 设计同向平行倾斜，作为楔形掏槽的单孔。考虑到单孔爆破振动持续时长在200 ms 内，两孔采用1、9 段爆破，时差大于300 ms；当两孔间距大于5 m 时，可在地表测点获得两孔的单自由面单孔振动波形。

图2 单自由面单孔爆破试验炮孔布置示意图Fig. 2 Layout of holes in single-hole blasting test with single free surface

在隧道分别进行3 种药量（1.0、1.2 和1.4 kg）单自由面单孔爆破，并在隧道正上方地表监测爆破振动得到振动波形图，各药量典型单孔波形如图3 所示。1.0、1.2 和1.4 kg 单孔振动最大振速依次为0.366、0.512 和0.897 cm/s。

图3 现场实测单自由面单孔振动波形Fig. 3 Single-hole vibration waveforms of single free surface measured on site

基于式(1) 及各参数计算公式，利用MATLAB 软件编程计算拟合函数f(t)。拟合波形前需将单孔波形截断并满足以下要求：(1)被截断波形峰值不大于单孔峰值振速的10%；(2) 截断时长保证N孔叠加时各段波形充分参与，据此选择起爆140 ms 后截断波形。图4 为1.4 kg 药量的拟合曲线和实测单孔波形对比图，曲线拟合的标准差为0.005 4，相关系数为0.997 1。

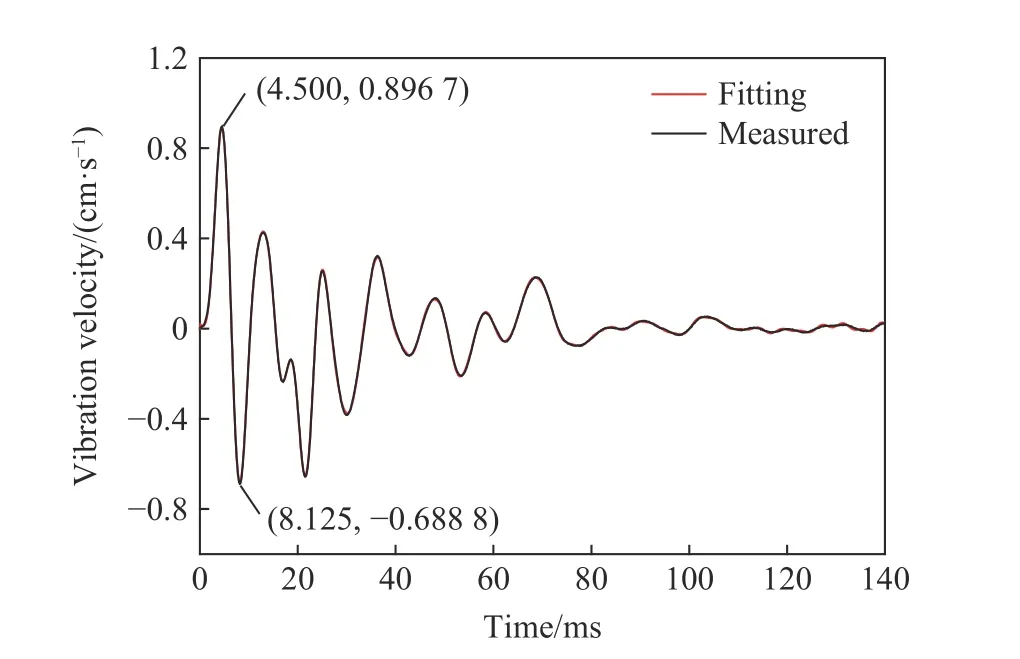
图4 1.4 kg 药量单孔波形拟合曲线与实测曲线对比Fig. 4 Comparison between fitting curve and measured curve of 1.4 kg charge single-hole waveform

2.2 掏槽爆破振动合成计算与分析

根据隧道断面初步设计8 孔掏槽，孔间延时以1 ms 为增量，在多个药量单孔波形函数v1(t)基础上，利用编程计算不同孔间延时下合成振速v(t,Δtn)，比较后选择最大合成振速不超标的最大药量和相应孔间延时为设计参数。

分别计算药量1.0、1.2 和1.4 kg 爆破后8 孔合成振速，相邻孔间延时取相同值Δt，为研究小间隔延时（10 ms 以下）与大间隔延时的差异，延时范围取1～50 ms。叠加计算函数如下：

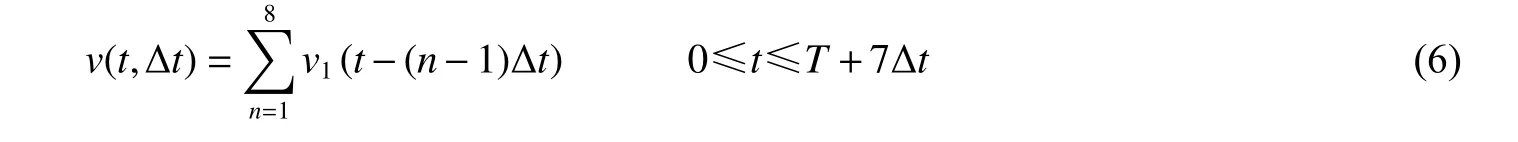
式中：v(t, Δt)为8 孔振动叠加函数；v1(t)为单自由面单孔波形时间全域函数；Δt为相邻孔间延时，取值1、2、 ··· 、50 ms，T=140 ms。

利用MATLAB 程序计算，得到1.0、1.2 和1.4 kg 相邻孔间延时1～50 ms 变化下8 孔叠加的所有振动曲线及最大合成振速。限于篇幅仅列出1.2、1.4 kg 药量各孔间延时的最大合成振速，如图5 所示，将同一孔间延时的正负最大振速值分别标出。在安全振速下，最大药量为1.4 kg，相应孔间延时取小间隔延时4～5 ms。

图5 单自由面下不同孔间延时8 孔叠加最大振速Fig. 5 Eight-holes maximum superimposed vibration velocity with different delays under single free surface

图5(b)中非绿色区间的较大延时时段，合成振速超过1.0 cm/s 安全指标，说明增大孔间延时并不一定使振速减小，大、小孔间延时均有振速超标时段，故仅靠施工经验难以准确设置。

对比图5 和图3，发现图5 中1.2、1.4 kg 药量下不同延时的最大合成振速均只能与图3 的单孔最大振速相近，而不会小于此值，这是一个重要特征。各爆破孔振动的错峰相消减振均发生在首爆孔第1 个波峰后的时段，因此即使采用最优延时干扰降振后，最大合成振速值只能为首爆孔振动波形第1 个波峰的振速；若单孔波形第1 个波峰的振速超安全振速值，采用任何孔间延时振速都将超标。

2.3 第二自由面形成前掏槽爆破延时与药量参数的设置

爆破最大振动通常出现在掏槽区，根据2.2 节的计算结果，1.4 kg 药量时8 孔掏槽峰值振速已非常接近1.0 cm/s 安全振速。为进一步降低振速，确保爆破振速不超标，对掏槽方式进行了优化，如图6 所示：采用双楔形掏槽，4 个主掏槽单孔药量降为1.2 kg；8 个辅助掏槽孔药量仍为1.4 kg。

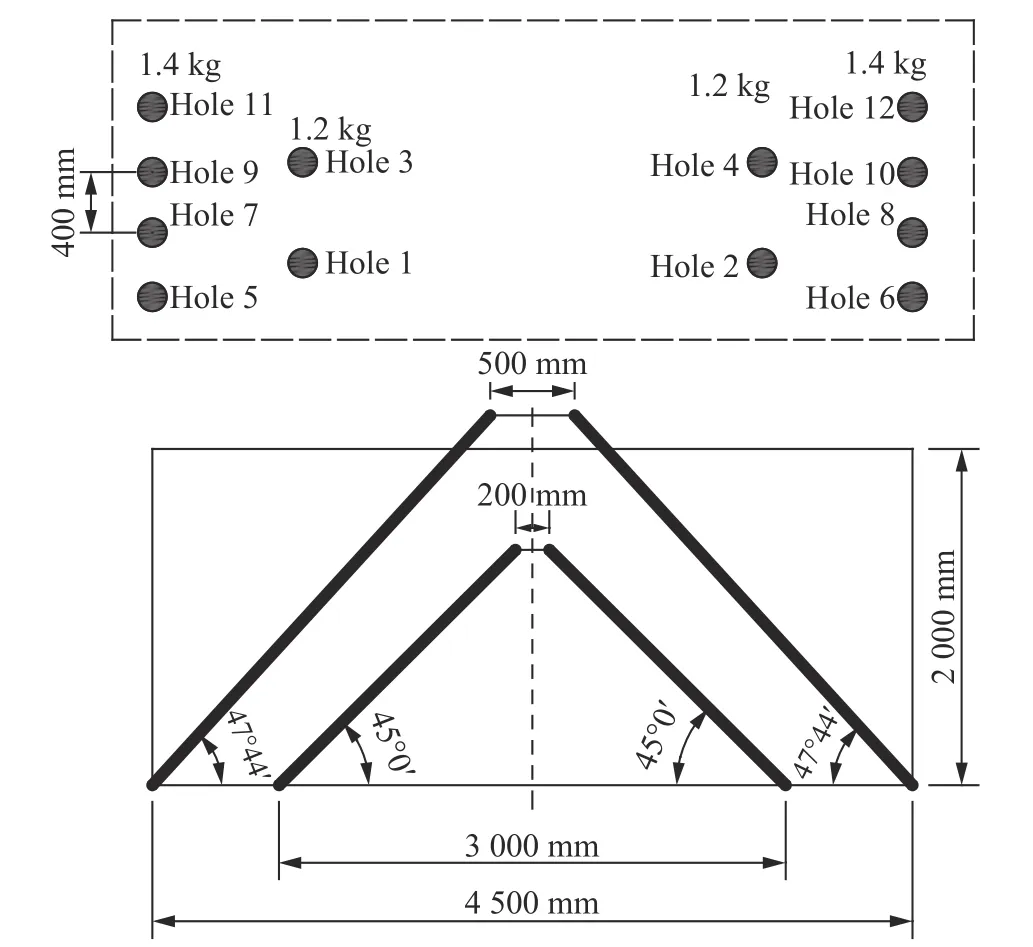
图6 优化后掏槽孔炮孔布置图Fig. 6 Layout of optimized cut holes

利用2.2 方法计算不同孔间延时合成振速峰值如图7 所示，确定主掏槽最优孔间延时为5 ms。

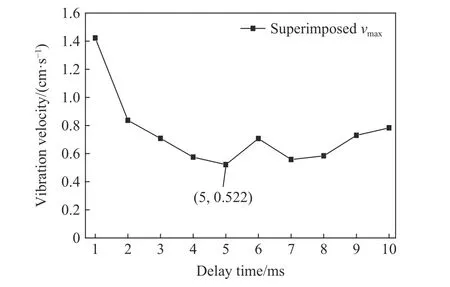
图7 1.2 kg 单自由面下不同延时4 孔叠加最大振速Fig. 7 Four-holes maximum superimposed vibration velocity of 1.2 kg with different delays under single free surface

2.4 观音桥隧道第二自由面形成时间的确定

根据作者前期对隧道普通雷管爆破研究[20]，第二自由面在起爆后54 ms 形成，为更准确确定自由面形成时间，设计了电子雷管短延时掏槽爆破现场试验，采用8 孔掏槽，考虑到孔间延时取较小值（如5 ms）时，第8 孔起爆（35 ms）尚未形成第二自由面；当孔间延时取8 ms 时，第8 孔起爆（56 ms）已形成第二自由面，故设计爆破试验孔间延时为8 ms。为避免首爆孔振速超标，第1 个起爆孔药量1.2 kg，其余7 孔药量均为1.4 kg。

在1.2、1.4 kg 单孔试验振动数据基础上，依据式(6)和MATLAB 程序，计算得到逐孔掏槽振动合成曲线（图8 中红线），在隧道正上方测得实际爆破振动曲线（图8 中黑线）。

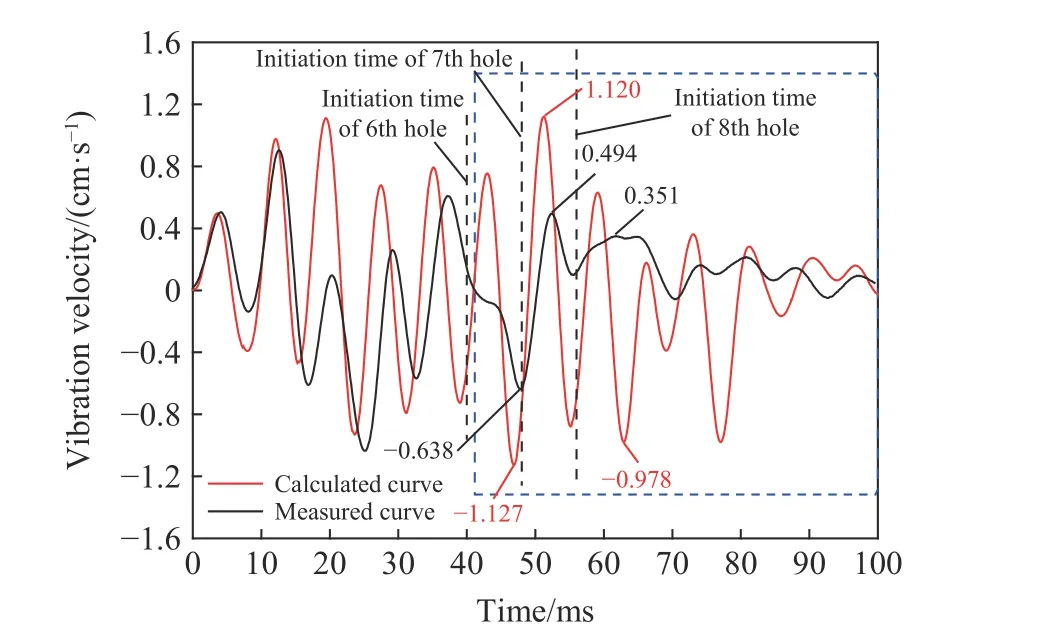
图8 8 ms 孔间延时的计算合成振动曲线与实测振动曲线对比图Fig. 8 Comparison between calculated superimposed vibration curve and measured vibration curve under 8 ms delay

比较图中两条曲线，前5 孔时段的爆破振动曲线与计算振动曲线基本一致，但两曲线从第6 孔起爆后开始（图中虚线框时段内）有显著差异，到第7、8 孔爆后实测最大振速较计算值均降低50% 以上，由此可判定起爆后48 ms（第7 孔起爆时刻）已形成第二自由面，这一时间较作者以前普通雷管试验缩小了6 ms 以上。

2.5 第二自由面形成后爆破参数的确定

如1.6.3 所述，目前不同类型炮孔（如主掏槽与辅助掏槽、掏槽与辅助孔）之间设较长延时，而在同类型孔间设置较短延时；下面将第二自由面形成后的炮孔延时分为不同类型炮孔（以主掏槽与辅助掏槽之间延时设置为例）、同类炮孔（以辅助掏槽孔之间为例）进行计算分析，并在已获知第二自由面形成时间情况下，探讨不同类炮孔间长延时设置的必要性。

为确定第二自由面形成后爆破参数，需首先获取双自由面下单孔爆破振动数据。

2.5.1 第二自由面形成后单孔爆破试验设计与振动数据分析

如2.4 所述，起爆后48 ms 已形成第二自由面，据此设计第二自由面形成后的单孔爆破试验。现场掏槽爆破设计如图9 所示，竖向相邻孔间距取0.5 m，孔口距根据孔深和掏槽角取为4.5 m；掏槽孔数和各孔药量根据需要设计。采用非电雷管逐孔爆破，相邻起爆孔间延时需大于200 ms，将1 孔设为1 段（起爆延时＜13 ms），2 孔起爆为9 段（310±30 ms），3 孔为13 段（650±50 ms），4 孔为17 段（1 200±90 ms）。在2 孔起爆时，因2 孔到1 孔爆破槽腔抵抗线过大仍属单自由面状态[20]，3 孔、4 孔爆破后振动波形均可视为双自由面条件下的单孔波形。

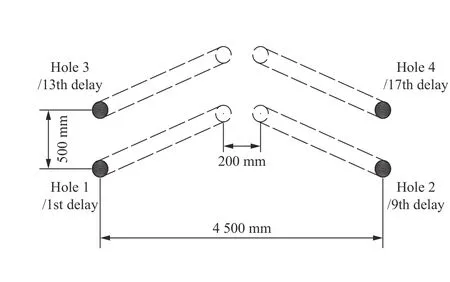
图9 第二自由面形成后单孔爆破试验炮孔布置示意图Fig. 9 Holes layout of single-hole blasting test after the second free surface is formed

通过现场试验，获得第二自由面形成后的1.4 kg 单孔爆破振动数据，与单自由面1.4 kg 单孔振动曲线对比如图10 所示，1.4 kg 单自由面最大振速为0.896 7 cm/s，第二自由面形成后最大振速为0.423 5 cm/s，第二自由面形成后最大振速较单自由面降低50%，证明第二自由面形成时间的判据是可靠的。

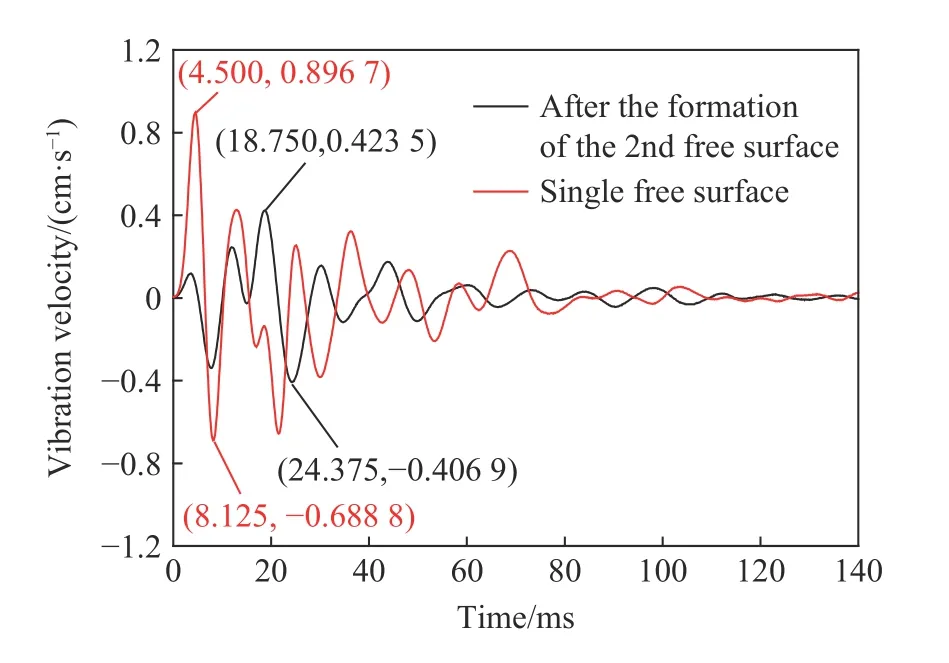
图10 第二自由面形成前后1.4 kg 单孔实测波形对比图Fig. 10 Comparison between measured single-hole waveforms of 1.4 kg before and after the second free surface is formed

根据1.2 节方法，对后两孔单孔爆破振动波形进行拟合，得到第二自由面形成后单孔波形函数v2(t)，以便于下一步计算延时爆破合成振速。

2.5.2 第二自由面形成后不同类炮孔（以主掏槽与辅助掏槽孔为例）孔间延时的确定

如2.3 节所述采用复式双楔形掏槽（4 个主掏槽孔，单孔药量为1.2 kg；8 个辅助掏槽孔，单孔药量为1.4 kg，参与计算炮孔12 个），以下计算主掏槽最后起爆孔与辅助掏槽首爆孔之间不同延时的合成振速，设主掏槽最后起爆孔与辅助掏槽首爆孔之间延时为ΔD，ΔD取值为5～50 ms，计算延时合成振速变化情况，据此确定最优时差。

需要说明，在进行主掏槽和辅助掏槽的叠加计算时，首先应根据ΔD的取值判断各辅助掏槽孔起爆时是否已形成第二自由面，再选择单孔波形函数公式。比如，当ΔD取值较小（如10 ms），辅助掏槽首爆孔起爆时（25 ms）第二自由面尚未形成，这时前5 个辅助掏槽孔仍需要按照单自由面单孔波形函数v1(t)进行叠加计算；当ΔD取较大值（如35 ms），辅助掏槽首爆孔起爆时（50 ms）已形成第二自由面，8 个辅助掏槽孔均采用第二自由面形成后单孔波形函数v2(t)进行叠加计算。其次确定同类炮孔的孔间延时，辅助掏槽孔间延时的取值，根据ΔD的取值分为单自由面和第二自由面形成后2 种情况，需要针对不同情况分类进行计算确定。而本节主要是分析ΔD、第二自由面形成时间和叠加振速之间的关系，为突出研究重点，统一将掏槽孔和辅助掏槽孔的孔间延时取值为5 ms。

综上考虑，按照ΔD的取值和第二自由面形成时间，分2 种情况进行叠加计算。

(1) 当3Δt1+ΔD≥50 ms 时，即辅助掏槽首爆孔起爆时已形成第二自由面，根据式(3)得：

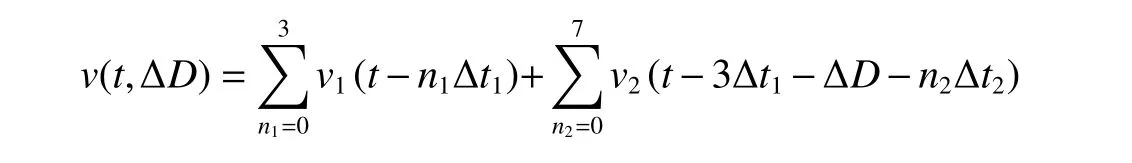
式中：v(t,ΔD)为合成波形函数；v1(t)为单自由面单孔波形函数；v2(t)为第二自由面形成后单孔波形函数；Δt1为主掏槽孔间延时，且Δt1=5 ms，Δt2为辅助掏槽孔间延时，且Δt2=5 ms，ΔD为掏槽最后起爆孔和辅助掏槽首爆孔延时间隔，且ΔD=5～50 ms。

(2)当3Δt1+ΔD＜50 ms 时，即辅助掏槽首爆孔起爆时未形成第二自由面，根据式(5)得：

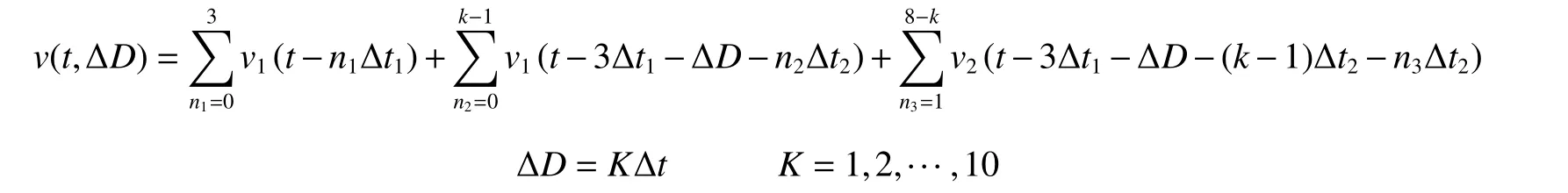
式中：k为第k个辅助掏槽孔(该孔起爆时形成第二自由面)。

利用MATLAB 程序计算延时ΔD与叠加最大振速之间的对应关系，如图11 所示。主掏槽最后孔起爆时间为15 ms，由2.4 节研究知起爆后48 ms 已形成第二自由面，即ΔD=35 ms 时已形成第二自由面。图11 中，ΔD取值35～50 ms 的叠加最大振速均为0.522 cm/s（均源自主掏槽爆破时段）；ΔD取值5～20 ms时，叠加最大振速基本都超过安全振速1.0 cm/s。第二自由面形成前后，叠加振速相差显著，且形成后爆破振速变化不大，振速值较小。最终确定优化ΔD取值应不小于35 ms。

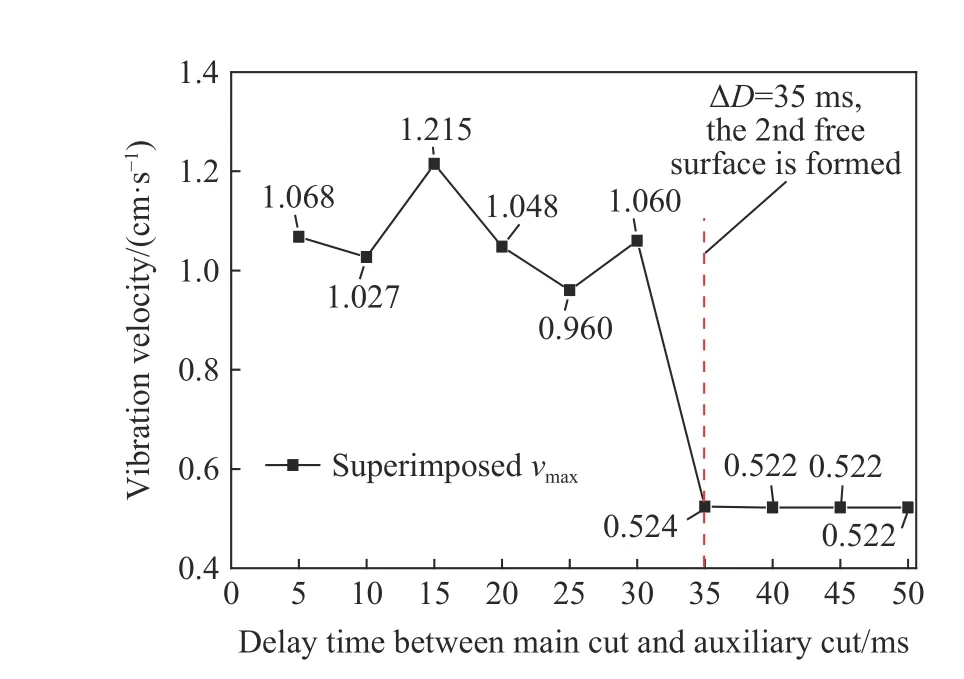
图11 主掏槽与辅助掏槽之间不同延时叠加最大振速Fig. 11 Maximum superimposed vibration velocity of different delays between main cut and auxiliary cut holes

选择ΔD=50 ms 即起爆后65 ms 进行现场试验（已形成第二自由面），试验采用与图6 相同的掏槽爆破参数。图12 是实测振动曲线与计算合成曲线的对比，主掏槽和辅助掏槽的计算最大振速和实测最大振速基本一致，验证了该方法是较可靠的。需指出因主掏槽药量为1.2 kg、辅助掏槽药量为1.4 kg，第二自由面形成前后振速变化不大。

图12 ΔD=50 ms 的计算曲线和实测曲线对比图Fig. 12 Comparison between calculated and measured curves when ΔD = 50 ms

2.5.3 第二自由面形成后同类炮孔（以辅助掏槽孔为例）孔间延时和药量的确定

如2.5.2 节所述，ΔD取值不小于35 ms，辅助掏槽孔起爆时已形成了第二自由面，辅助掏槽孔的单孔药量为1.4 kg。根据第二自由面形成后1.4 kg 单孔爆破波形函数v2(t)进行8 孔振动叠加计算，孔间延时取值1～10 ms，计算结果及与单自由面振动叠加对比如图13 所示，得到辅助掏槽孔的最优延时范围为4～5 ms；从图13 可看出同一延时下，第二自由面形成前后的合成振速差异是非常显著的。

图13 第二自由面形成前后1.4 kg 不同延时下8 孔叠加最大振速对比图Fig. 13 Comparison of 8-holes maximum superimposed vibration velocity of 1.4 kg under different delays before and after the formation of the second free surface

辅助孔起爆时，爆破条件较掏槽爆破有所改善且振速下降明显，通常药量可较掏槽孔减少15%～20%，在辅助孔药量取1.0 kg 条件下需确定孔间延时参数。

限于现场施工条件，未能采集第二自由面形成后1.0 kg 单孔波形。为验证5 ms 延时的降振效果是否同样适用于辅助孔，在隧道中部辅助孔区域进行不同延时爆破对比试验，延时取3、5、8 ms 时分析其爆破振速变化，炮孔布置与延时设计参见图14 的对比区域，为保持自由面条件一致，设计第1、2 排对比8、5 ms 延时的振速；3、4 排对比3、5 ms 延时的振速；相应延时时段振动波形如图15 所示。

图14 辅助孔不同孔间延时振动强度对比区域Fig. 14 Vibration velocity comparison area of auxiliary holes with different delays

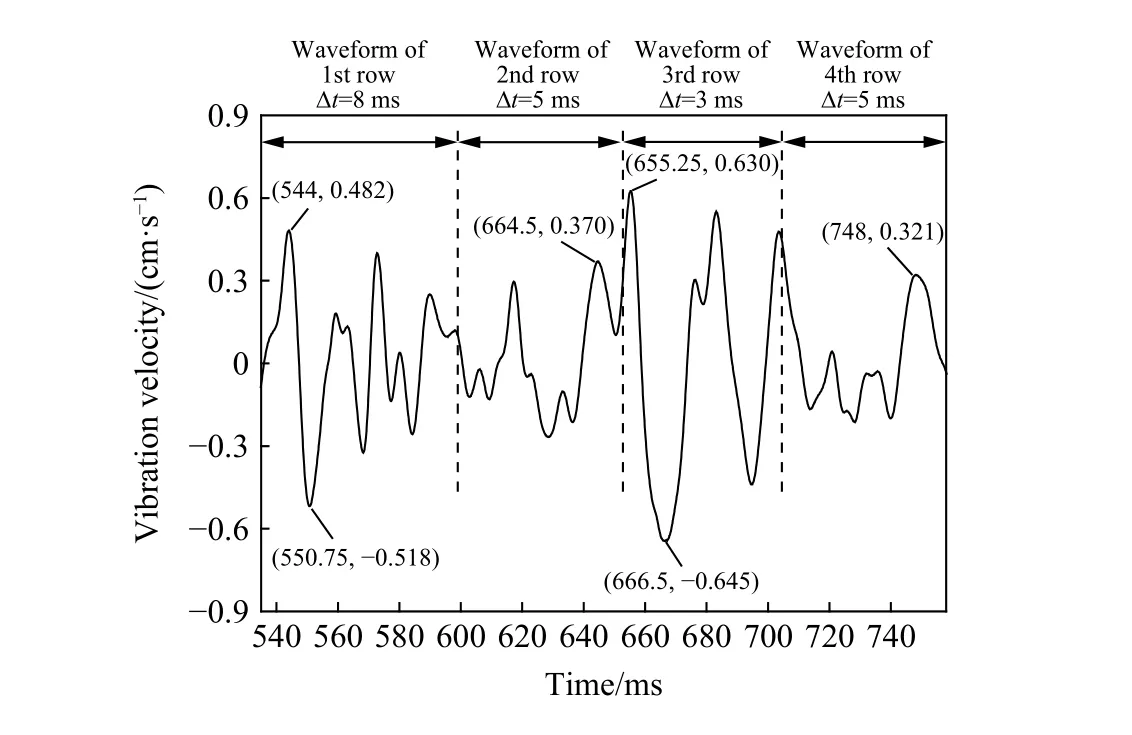
图15 辅助孔不同延时的爆破振动波形Fig. 15 Blasting vibration waveform of auxiliary holes with different delays

由图15 可得，第1 排(8 ms)的最大振速为0.518 cm/s，第2 排(5 ms)的最大振速为0.37 cm/s，5 ms 延时最大振速小于8 ms，振速相差0.148 cm/s；第3 排(3 ms)的最大振速为0.645 cm/s，第4 排(5 ms)的最大振速为0.321 cm/s，5 ms 延时小于3 ms 最大振速，振速相差0.324 cm/s。与延时3、8 ms 相比，5 ms 延时降振效果更好，这表明辅助孔的延时取值可参照第二自由面形成后1.4 kg 单孔波形的叠加计算结果。

以上研究表明：（1）第二自由面形成时间对掏槽区的参数设置至关重要，对于隧道电子雷管爆破方式而言，孔位布设不再局限于传统掏槽区概念，以第二自由面形成时间为标准进行隧道炮孔类型设计更为精确；（2）第二自由面形成后，增大主掏槽最后起爆孔与辅助掏槽首爆孔之间的延时对降低振速无明显作用。

2.6 现场验证

根据以上研究结果，确定爆破参数为：设计主掏槽4 孔、辅助掏槽孔8 孔；主掏槽单孔药量1.2 kg，辅助掏槽单孔药量1.4 kg，辅助孔单孔药量1.0 kg，周边孔单孔药量0.6 kg，底板孔单孔药量0.8 kg；掏槽孔、辅助掏槽孔的孔间延时取5 ms，考虑辅助孔和底板孔的单孔药量有所减少，且已出现第二自由面，孔间延时取较小值4 ms。周边孔光面爆破需要尽量小的延时间隔，周边孔设计延时3 ms；掏槽与辅助掏槽孔的排间延时50 ms，辅助掏槽与辅助孔、辅助孔之间的排间延时40 ms；实际爆破炮孔布置图如图16 所示。图17 是在地表正上方实测的振动曲线，从图中可以看出，全时程最大振速为0.677 cm/s，远小于安全振速1.0 cm/s，降振效果显著。

图16 爆破试验炮孔布置图Fig. 16 Holes layout of blasting test

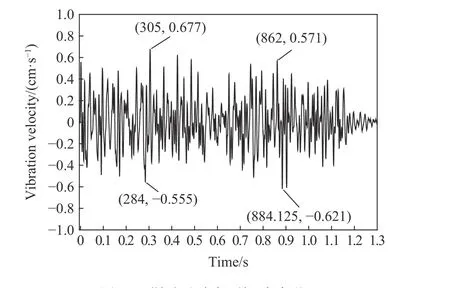
图17 爆破试验实测振动波形Fig. 17 Measured vibration waveform of blasting test

3 结 论

（1） 提出了一种基于安全振速的电子雷管爆破参数设计方法，即采用现场试验数据与数学方法结合，充分利用电子雷管起爆时间的准确性计算合成振速，在计算不同延时的多孔合成振速及比较不同药量的最大合成振速后确定爆破参数。与传统经验方法相比，该方法通过计算精确设置孔间延时，确定最大单孔药量，有效控制振速并实现高效进尺，有利于发挥电子雷管延时准确的优势。

（2） 利用电子雷管延时准确的特性设计现场试验，得到第二自由面较准确的形成时间。研究发现观音桥隧道爆破起爆后48 ms 已形成了第二自由面，与采用非电雷管试验相比准确性提高6 ms 以上。

（3） 根据第二自由面形成时间设计不同自由面数量的单孔爆破试验，计算新自由面形成前、后的延时爆破合成振速，据此确定爆破全时程不同类型炮孔的药量和孔间延时。这种技术较过去仅能确定单自由面爆破参数是一个突破。

（4） 对于隧道电子雷管爆破方式而言，孔位布设不再局限于传统掏槽区概念，以第二自由面形成时间为标准进行隧道爆破中各类型炮孔的参数设计更为精确；第二自由面形成后，增大主掏槽最后起爆孔与辅助掏槽首爆孔之间的延时对降低振速无明显影响。