新型发射药爆炸TNT 当量系数的实验研究*

高金明，曾 丹，孙 磊，陈 力，何成龙

（1. 中国兵器工业火炸药工程与安全技术研究院，北京 100053；2. 东南大学爆炸安全防护教育部工程研究中心，江苏 南京 211189；3. 中北大学机电工程学院，山西 太原 030051）

高能发射药可以使身管武器发射动能增高、质量效率和射程增大，提高弹药威力。为满足超远射程或高膛压反装甲弹药的发射需求，进一步提升高膛压火炮的穿甲威力，快速批量生产能量高、力学性能好的新型发射药迫在眉睫[1]，这也对新型发射药生产车间的抗爆隔离设计提出了要求。

冲击波超压不仅是发射药的重要性能指标，也是火炸药、火工品生产车间进行抗爆隔离设计的重要安全参数[2]。由于装药随载体运动爆炸产生的冲击波超压测试较复杂, 量测冲击波超压主要以静爆实验为主[3]。汪嗣良等[4]基于锰铜压阻高压量程测试系统，对压装CL-20 炸药开展了静爆实验，基于信号波形在同轴电缆中的衰减推导出未衰减的实际爆轰波压力。王代华等[5]选用性能优良的ICP 压力传感器，基于存储测试原理测定了某型弹的冲击波超压、正压持续时间和冲量。牛余雷等[6]研究了炸药爆轰参数与冲击波超压之间的关系，基于相似理论和超压数据，计算出了炸药的爆轰参数。段晓瑜等[7]对3 种炸药不同距离的反射超压进行了测试，首次发现幂指数拟合公式在取对数后为线性关系。王鹏等[8]开展了水下静爆实验，通过高速摄影研究了炸药的爆轰性能，揭示了超压及炸药能量在水中的输出规律。现有的静爆冲击波超压计算模型较多, 比较经典的是基于相似律发展的Henrych 公式[9]、Baker 公式[10]和Sadovskyi 公式[11]等。聂源等[12]则基于Baker 公式[10]进行修正，得到了沿装药不同比例距离和方位角处的动态爆炸冲击波超压峰值。

除了超压，爆炸冲量是另一项非常关键的战技和安全指标[13-14]，同样能够为抗爆隔离设计提供依据。蔡林刚等[15]基于一种简化的内爆载荷模型计算发现，有效作用时间的长短与冲击波作用时间、冲击波和准静态压力峰值以及舱室的尺寸有关。牟金磊等[16]推导了冲击波压力/正压作用时间和比冲量与板厚之间的关系，发现比冲量随正压作用时间延长而增大；在刚性壁的情况下，比冲量为自由场的2 倍。张德志等[17]基于大量实验数据进行分析，发现球形装药爆炸冲击波正反射超压峰值在比例距离0.098～0.5 m·kg-1/3范围内呈指数衰减。龚苹等[18]基于地面压力传感器、自由场压力传感器和自由场波速法量测冲击波超压，得到了入射冲击波超压和反射冲击波超压的变化规律。

我国研制的某新型发射药H 在批量生产、运输和存储过程中具有爆炸危险性，因为尚不明确其爆炸威力的TNT 当量数据，所以相关生产工房防护设计及安全距离划分等问题至今无法解决。为此，本文中开展一系列的大当量静爆实验，测量得到相同环境下10 kg TNT 和两种配比的高能发射药的自由场爆炸冲击波时程数据，揭示这两种高能发射药的爆炸冲击波传播规律，计算不同比例距离处发射药超压及比冲量TNT 当量系数，以期为相关抗爆结构设计和安全风险评估提供基础参数。

1 现场实验

1.1 实验方案

本次实验所涉及的新型发射药有两种配比，分别为H1 和H2。TNT 炸药选择标准军用片状产品。为降低装药形状和外壳约束条件对测试结果的影响，发射药（H1、H2）及TNT 均采用圆柱状纸筒装药。纸筒的外径为246.5 mm，高度为250.0 mm，高径比近似为1∶1。为保证发射药和TNT 能够完全爆轰，采用8 号工业雷管起爆，JH-2 药柱传爆。JH-2 传爆药柱为压制药柱，质量为123 g，预留2 个雷管安装孔。实验时，先将JH-2 药柱竖直插入TNT 或发射药装药中，然后再将雷管插入JH-2 药柱的雷管安装孔内（见图1）。对发射药H1、H2 和TNT 炸药共进行3 组实验，每组实验选用一种药剂。为了降低实验环境对测试结果的影响，对每种药剂均进行5 发实验，共计15 发爆炸实验，每发实验所用药量均为10 kg。其中，TNT 实验作为对照组，发射药H1、H2 实验作为实验组。

图1 相关炸药外形尺寸特征Fig. 1 Size characteristics of related explosives

1.2 实验场地布置及测试系统

实验在专用测试靶道进行，测试靶道如图2所示，共有2 条同心的地面测带。2 条测带均为1.0 m 宽，呈10°夹角，爆心及测带周围30 m 范围内无明显影响冲击波传播的障碍物。为降低TNT、发射药装药形状和地势对冲击波流场的影响，实验过程中，在2 个测带方向上与爆心相同距离处布置了压力传感器。每条测带共计布置了13 个测点，与爆心距离分别为2、3、5、7、10、15、20、25、30、40、50、60 和85 m。

图2 专用测试场Fig. 2 Special test field

为降低偶然误差对测试结果的影响，除爆炸近区（前3 个测点）外，其余测点布置PCB 系列（113B24、113B21、113A28、113B28 型号）及Kistler 系列（603CBA00014.0 型号）两种不同系列的壁面式高频动态压力传感器（见图3）。

图3 测点传感器布置Fig. 3 Layout of sensors at measuring points

测试系统由信号采集系统、信号传输系统、数据采集系统、零时信号触发系统以及终端数据记录系统组成，测试系统示意图如图4 所示。

图4 测试系统连接示意图Fig. 4 Test system connection diagram

2 实验结果与分析

2.1 实验数据修正

2.1.1 气象条件修正

为消除气象条件对实验测试结果的影响，对实验数据进行气象修正处理，保证实验数据的一致性和可比性。将超压峰值、爆心距离、正压作用时间、比冲量等参数修正到标准大气条件下的数值，具体公式如下：

式（1）～（4）中的相关物理参数如表1 所示。

表1 式（1）～（4）中的相关物理参数Table 1 Physical parameters for formulas (1) - (4)

2.1.2 异常数据剔除

为剔除在测量过程中由于突然的环境条件变化（如飞石等的冲击、振动、电源电压突变等）导致的异常测量数据，首先对气象修正后的数据进行格拉布斯法误差分析，具体方法如下。

设测量得到的实验数据为X1、X2、……、Xm（m为测试组中的数据数量，X1～Xm为测量得到的超压峰值或比冲量数据），其算术平均值Xa和标准差S分别为：

取危险率a=5.0%，查格拉布斯法A(m,a)值得到危险率a=5.0%的A值，若di/S≥A(m,a)，则数据Xi应剔除。

2.2 TNT、H1、H2 爆炸威力分析

2.2.1 TNT 爆炸冲击波超压峰值

对TNT 爆炸产生的冲击波超压峰值剔除误差后的结果进行算术平均处理，得到不同爆心距离R处冲击波超压峰值平均值 ΔpTNT,a，如表2所示。

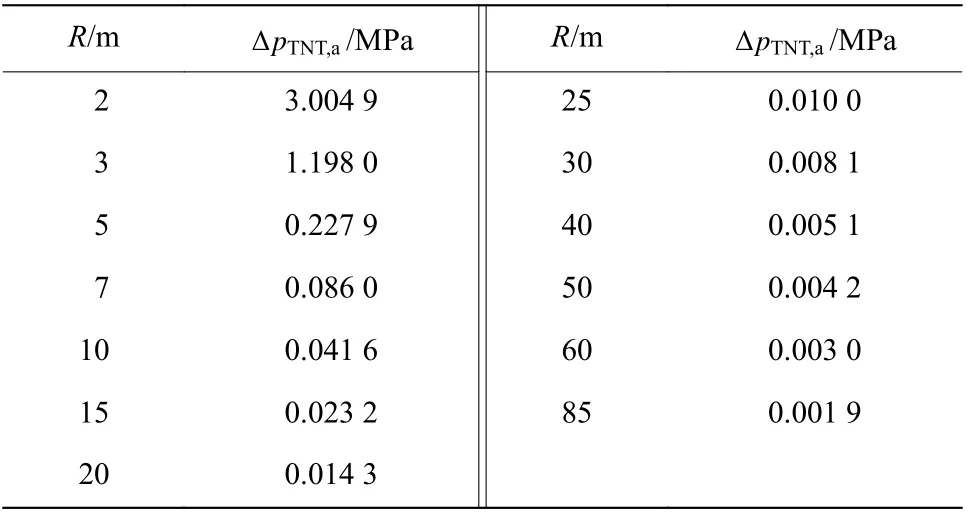
表2 不同爆心距离处10 kg TNT 爆炸产生的冲击波超压峰值平均值Table 2 Average values of shock wave overpressure peaks induced by explosion of a 10-kg TNT charge at different distances from the explosion center

对得到的TNT 爆炸冲击波超压峰值平均值按爆炸相似律进行三项式拟合，得到10 kg TNT 爆 炸 冲 击 波 超 压 峰 值 ΔpTNT,a随 比 例 距 离Z的变化曲线：

拟合结果的相关系数为0.971 08，残差平方和为5.046 25。

将式（8）与Sadovskyi 公式及软质地面经验公式[19]进行对比分析，如图5 所示。从图5 可以看出，在比例距离大于1.2 m·kg-1/3的范围内，实测超压峰值及拟合曲线随比例距离的变化与以上两种经验公式[19]符合较好，95%置信区间内显著一致，说明实验条件、测试系统及TNT 超压数据准确可靠，TNT 拟合曲线能够作为发射药爆炸冲击波TNT 当量计算的基准数据。但是，在比例距离小于1.2 m·kg-1/3的范围内，实验数据和现有公式[19]还是有一定的差距，这主要是由于现有公式[19]是基于球形装药建立的，而在比例距离小于1 m·kg-1/3的范围内炸药形状的影响不可忽略。这就凸显了开展圆柱形装药TNT 爆炸实验的必要性。

图5 10 kg TNT 爆炸产生的冲击波超压峰值随比例距离的衰减（对数坐标）Fig. 5 Attenuation of shock wave overpressure peak induced by explosion of a 10-kg TNT charge with scaling distance in logarithmic coordinates

2.2.2 H1、H2 爆炸冲击波超压峰值

对气象修正和误差剔除后的发射药（H1、H2）爆炸冲击波超压峰值分别进行算术平均处理，得到不同爆心距离处的超压峰值（ ΔpH1,a，ΔpH2,a），如表3 所示。

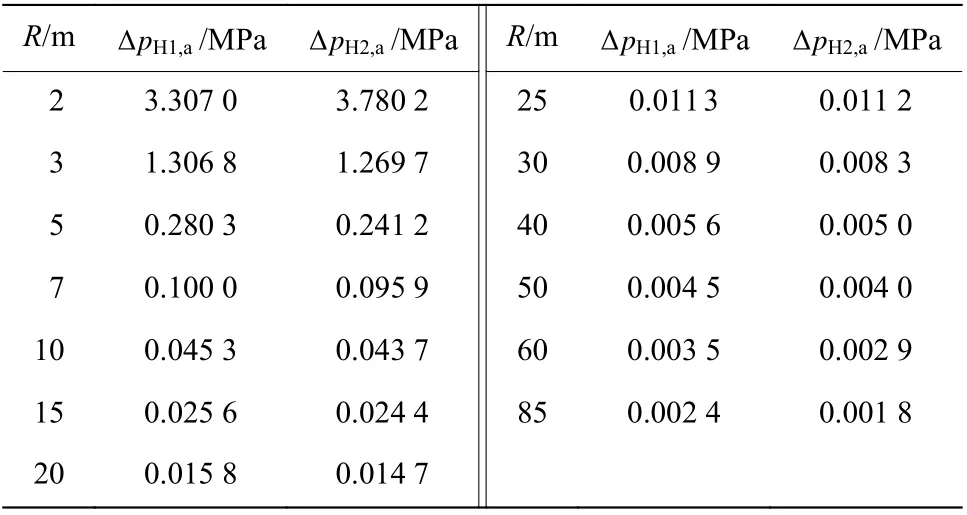
表3 不同爆心距离处发射药（H1、H2）爆炸冲击波超压峰值平均值Table 3 Average values of shock wave overpressure peaks induced by explosion of propellants (H1, H2)at different distances from the explosion center

由于H1、H2 两种发射药的超压TNT 当量系数未知，其爆炸TNT 当量和比例距离无法确定，因此对超压峰值按三项式进行数据拟合，得到TNT 和两种新型发射药在15 ℃、101.325 kPa标准大气压条件下的超压峰值与距离R的关系分别为：拟合曲线的相关系数分别为0.971 08、0.970 07、0.966 21，残差平方和分别为5.046 25、1.677 36、5.925 6。

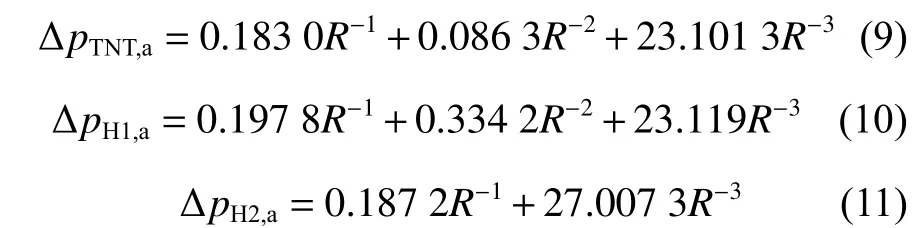
图6 给出了TNT 和H1、H2 冲击波超压峰值随距离的变化曲线。从图6 可以看出，在2～100 m 爆心距离范围内，H1、H2 爆炸产生的冲击波超压峰值均大于TNT 爆炸产生的冲击波超压峰值；当爆心距离小于10 m 时，H2 爆炸产生的冲击波超压峰值大于相同质量H1 爆炸产生的冲击波超压峰值；当爆心距离大于10 m时，H1 爆炸产生的冲击波超压峰值大于H2 爆炸产生的冲击波超压峰值，且随爆心距离的增大，H1 爆炸产生的冲击波超压峰值与TNT 爆炸产生的冲击波超压峰值越接近。测点距H 1、H2 和TNT 爆心越近，该测点处的超压峰值衰减越快，说明H1、H2 爆炸产生的冲击波超压峰值衰减规律与TNT 爆炸产生的冲击波超压峰值衰减规律相同，符合爆炸相似律。

图6 10 kg TNT、H1、H2 爆炸产生的冲击波超压峰值随爆心距离的变化（对数坐标）Fig. 6 Changes of shock wave overpressure peaks induced by explosions of three 10-kg explosive charges (TNT, H1, H2)with the distances from the explosion centers in logarithmic coordinates, respectively

2.2.3 TNT、H1、H2 爆炸冲击波比冲量

爆炸威力不仅与冲击波超压峰值有关，也与正压作用时间有关，一般采用比冲量表征，比冲量为冲击波超压曲线对正压作用时间的积分。同样，对气象修正和误差剔除后的TNT、H1、H2 爆炸产生的冲击波的比冲量分别进行算术平均，得到不同距离R处的比冲量。对比冲量按三项式进行数据拟合，得到TNT 和H1、H2 在标准环境下爆炸产生的冲击波的比冲量与爆心距离的关系，分别为：

拟合曲线的相关系数分别为0.999 63、0.999 68、0.999 15，残差平方和分别为4.836 72、6.418 52、0.062 96。图7 给出了TNT 和H1、H2 爆炸产生的冲击波的比冲量随距离的变化曲线。从图7 可以看出，在1～100 m的距离范围内，相同质量的 H1、H2 爆炸产生的冲击波的比冲量均大于TNT 爆炸产生的冲击波的比冲量；当爆心距离小于6 m 时，H1、H2 爆炸产生的冲击波的比冲量相差不大；当爆心距离大于6 m 时，H2 爆炸产生的冲击波的比冲量逐渐超过H1 爆炸产生的冲击波的比冲量，且随爆心距离的增大，H1 与H2 爆炸产生的冲击波的比冲量差值逐渐稳定。H1、H2 爆炸产生的冲击波的比冲量的衰减规律与TNT 爆炸产生的冲击波的比冲量的衰减规律相同，距离爆心越近，比冲量衰减越快。

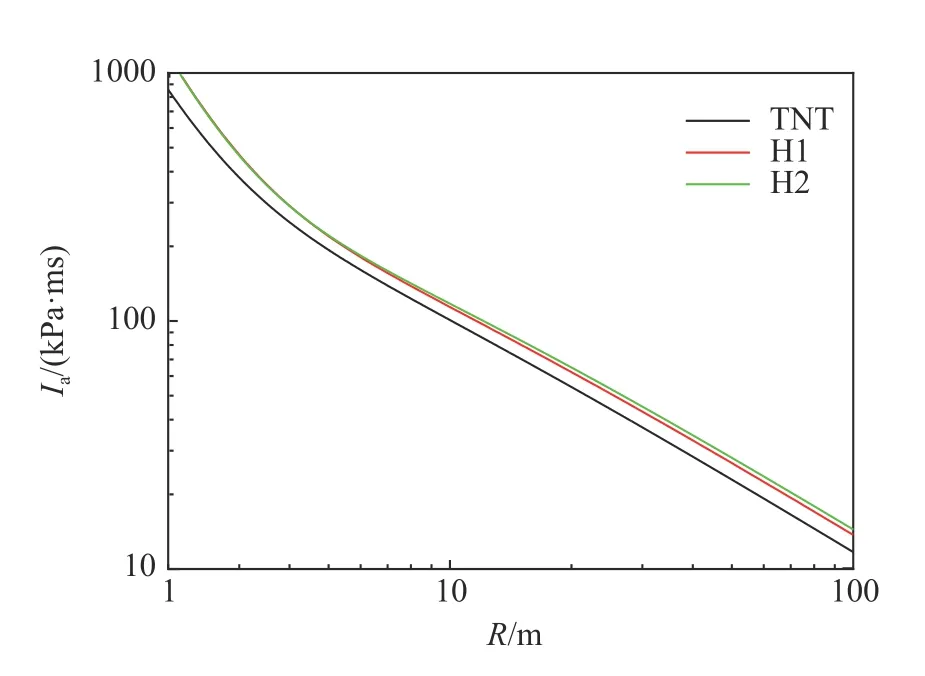
图7 10 kg TNT、H1、H2 爆炸产生的冲击波的比冲量随爆心距离的变化（对数坐标）Fig. 7 Changes of shock wave specific impulses induced by explosions of three 10-kg explosive charges (TNT, H1, H2)with the distances from the explosion centers in logarithmic coordinates, respectively

3 TNT 当量系数确定

3.1 修正的超压TNT 当量系数计算方法

现有燃烧爆炸品TNT 当量实验方法中，通过被试样品的拟合公式计算各测点的冲击波超压峰值，然后将计算得到的超压峰值代入测试得到TNT 数据拟合公式（超压峰值-比例距离关系）中，计算TNT 爆炸产生相同超压峰值时的比例距离ZTNT，并按下式计算各测点对应比例距离处Zce的超压TNT 当量系数：

式中：Wce为被试样品的质量，WTNT为TNT 的质量。

此方法在计算被试样品比例距离时，采用的是被试样品的实际质量，不是被试样品的TNT 当量。因此，通过公式（12）计算得到的超压TNT 当量系数偏小，在抗爆结构设计和安全距离划分时偏危险。

考虑到上述计算方法存在的不足，对该计算方法进行修正。首先，根据被试样品拟合公式计算不同距离处的冲击波超压峰值；然后，将计算结果代入TNT 拟合公式（超压峰值-比例距离关系）中，计算TNT 爆炸产生相同超压峰值时的比例距离Zi；接着，通过下式：

计算得到距离Ri处相同比例距离Zi时被试样品的TNT 当量Wpi；最后，通过下式：

计算被试样品在距离Ri处的超压TNT 当量系数Epi。

3.2 超压当量系数确定

图8 给出了原计算方法得到的H1、H2 超压TNT 当量系数及修正后的超压TNT 当量系数随比例距离的变化曲线。从图8 可以看出，H1、H2 发射药的超压TNT 当量系数并非恒定值，修正前后超压TNT当量系数随比例距离的变化规律一致，但修正前系数值比修正后系数值小，甚至在比例距离小于3 m·kg-1/3时H1 超压TNT 当量系数小于1，这与图7 所示发射药和TNT 爆炸产生的冲击波的超压峰值关系相反。因此，原方法计算得到的超压当量系数对于抗爆结构设计和安全距离划分更危险，修正后的TNT 当量系数能更好地反映发射药的爆炸威力。

图8 10 kg H1、H2 爆炸产生的冲击波超压TNT 当量系数峰值随比例距离的变化Fig. 8 Changes of peak TNT equivalent coefficients for overpressures of shock waves induced by explosions of two 10-kg propellants (H1, H2) with proportional distance, respectively

从修正后超压当量系数看，H1 超压TNT 当量系数在比例距离0～18 m·kg-1/3范围内递增，由1.10 增大到1.34；在比例距离18～40 m·kg-1/3范围内递减，由1.34 逐渐减小并稳定于1.32。与H1 超压TNT 当量系数随比例距离的变化不同，H2 超压TNT 当量系数随比例距离的增大单调递减。在比例距离0～18 m·kg-1/3范围内，H2 超压TNT 当量系数衰减较快，由1.26 下降至1.07；在比例距离18～40 m·kg-1/3范围内，H2 超压TNT 当量系数衰减减慢并趋于恒定值，由1.07 下降至1.05。总体来说，H1、H2 修正后的超压TNT 当量系数大于1。

3.3 比冲量当量系数确定

与修正后超压TNT 当量系数计算方法相同，图9 给出了H1、H2 修正前后比冲量TNT 当量系数（EI）随比例距离的变化曲线。从图9 可以看出，修正前后H1、H2 的比冲量TNT 当量系数的变化规律相似，均呈现先减小后增大的趋势，但修正前系数值比修正后系数值小，尤其在爆炸近区修正后当量系数比修正前大约20%。显然，修正后的系数值能更精确地表征发射药的爆炸威力。从修正后比冲量TNT 当量系数看，随着比例距离的增大，H2 比冲量TNT 当量系数下降到最小值1.13，小于同位置的H1 比冲量TNT 当量系数最小值1.22。不同的是，H2 比冲量TNT 当量系数变化较大，在比例距离0～2 m·kg-1/3范围内，从1.29 迅速减小为1.13；在比例距离2～40 m·kg-1/3范围内，从1.13 迅速增大并趋于稳定值1.33。随着比例距离进一步增大，H2 比冲量TNT 当量系数大于H1 的。

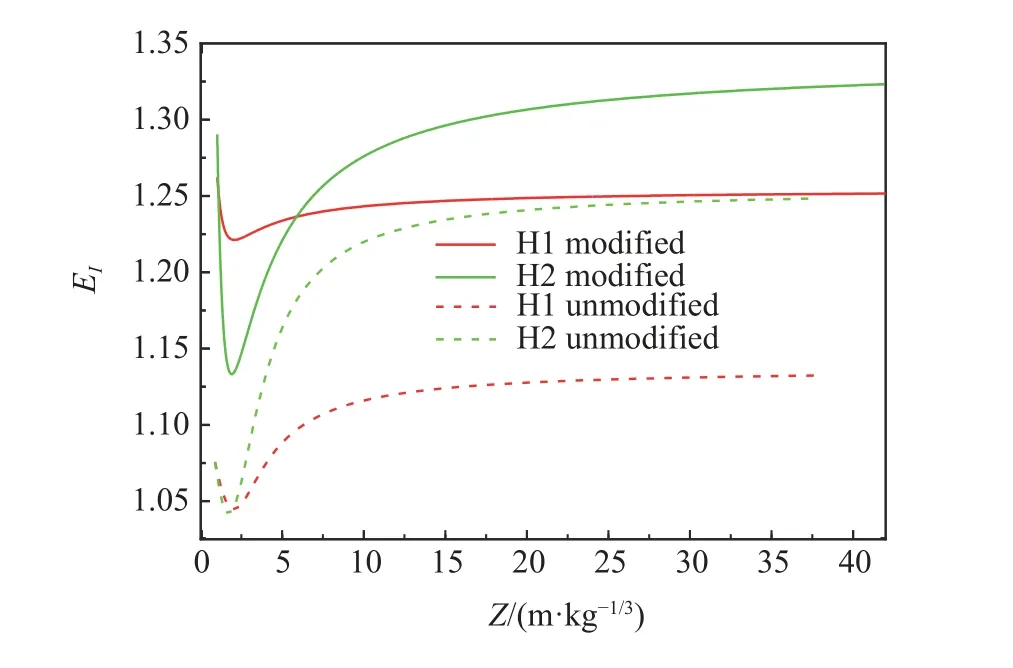
图9 10 kg H1、H2 爆炸产生的冲击波比冲量TNT 当量系数峰值随比例距离的变化Fig. 9 Changes of peak TNT equivalent coefficients for specific impulses of shock waves induced by explosions of two 10-kg propellants (H1, H2)with proportional distance, respectively

4 结 论

（1）实测TNT 超压峰值拟合曲线与比例距离的关系与Sadovskyi 公式、软质地面经验公式计算的结果符合性较好，95%置信区间内显著一致，说明本文的实验条件、测试系统及测试数据准确可靠，TNT 拟合曲线能够作为发射药爆炸冲击波TNT 当量计算的基准数据。

（2）现有爆炸品冲击波TNT 当量实验方法中，对被试样品比例距离的计算采用的是被试样品的实际质量，而非TNT 当量，依据该方法计算的结果进行抗爆结构设计和安全距离设定危险性偏高。本文中提出的修正的比例距离计算方法，能更准确地计算被试样品的TNT 当量系数，进而提高抗爆结构设计的安全性。

（3）H1、H2 两种新型发射药爆炸冲击波衰减规律与TNT 的相似，符合爆炸相似律，相同质量的H1、H2 爆炸产生的冲击波超压峰值和比冲量均大于TNT 的。随着比例距离的增大，H1 的超压TNT 当量系数先增大后减小，最大值为1.34，H2 的超压TNT 当量系数逐渐减小，最大值为1.26。两种新型发射药的比冲量TNT 当量系数均随比例距离的增大先减小后增大，H1 的比冲量TNT 当量系数最大值为1.26，H2 的比冲量TNT 当量系数最大值为1.33。