考虑履带滑转滑移的电驱动履带车辆转向控制
2021-11-15盖江涛刘春生马长军沈宏继
盖江涛, 刘春生, 马长军, 沈宏继
(1.中国北方车辆研究所, 北京 100072;2.车辆传动重点实验室, 北京 100072;3.63963部队, 北京 100072)
0 引言
在履带车辆的实际转向过程中,总是伴随着高速侧履带接地段的滑转和低速侧履带接地段的滑移[1]。国内外学者针对考虑履带打滑的车辆转向机理进行了深入研究[2-7],在考虑高速履带车辆转向离心力和履带滑动的条件下,根据剪切应力- 剪切位移关系模型,建立了计算两侧履带与地面之间作用力、转向阻力矩、转向半径、转向角速度等参数的运动学和动力学模型。分析研究结果表明,与传统转向理论的计算结果相比,考虑履带与地面之间滑动时的转向半径是传统理论计算值的1.5倍甚至更高,实际转向角速度是理论转向角速度的50%~65%. 以上文献中建立的转向方程均为复杂的超越方程,只能通过数值计算迭代求解,但其研究结果可为电驱动履带车辆转向机构的设计和转向控制提供理论支持。
传统液力机械综合传动车辆的转向控制是开环的,无法实现较精确的转向轨迹控制。对于电驱动履带车辆,由于电机优良的调速特性,车辆的精确转向控制是有条件实现的。为保证电驱动履带车辆的精确转向,在解算电机控制指令时需要考虑车辆转向过程中履带滑转滑移的影响,以准确实现转向目标。目前,电传动履带车辆转向控制策略有转速控制策略及转矩控制策略,但是均未考虑履带打滑对转向轨迹控制精度影响[8-12]。本文对表征履带车辆转向过程滑转滑移特性的转向半径修正系数及转向角速度修正系数进行分析,在此基础上提出考虑履带滑转滑移的转向控制策略,利用转向半径修正系数及转向角速度修正系数对驱动电机转速控制指令进行修正,精确实现了电驱动履带车辆的转向目标。结果表明,本文提出的控制策略可应用于无人履带车辆的转向轨迹精确控制。
1 电驱动履带车辆转向特性分析
1.1 履带滑转滑移条件下的车辆转向特性
图1所示为履带车辆转向平面运动示意图。图1中,B为履带中心距,L为履带接地段长度,C为车辆几何中心,Ol与Oh分别为低速侧履带与高速侧履带的瞬时转向中心,Cl、Ch分别为内侧、外侧履带接地面中心,Os为车辆实际瞬时转向中心,Ot为车辆理论瞬时转向中心,Sl与Sh分别为低速侧履带与高速侧履带瞬时转向中心的横向偏移量,ωs为车辆实际转向角速度,ωt为车辆理论转向角速度,Rs为实际转向半径,Rt为理论转向半径,vs,l为低速侧履带实际卷绕速度,vs,h为高速侧履带实际卷绕速度,vt,l为低速侧履带理论卷绕速度,vt,h为高速侧履带理论卷绕速度。
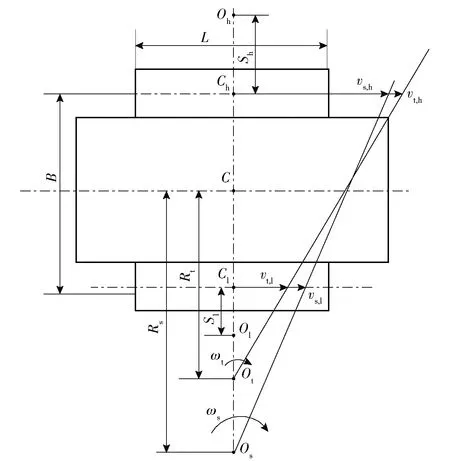
图1 履带车辆转向平面运动示意图Fig.1 Steering plane motion diagram of tracked vehicle
对履带滑转滑移条件下的车辆转向运动学特性进行分析。
定义转向半径修正系数fρ为履带车辆实际相对转向半径ρs与理论相对转向半径ρt的比值:
fρ=ρs/ρt=Rs/Rt.
(1)
定义转向角速度修正系数fω为ωs与ωt的比值:
fω=ωs/ωt.
(2)
车辆理论相对转向半径及理论转向角速度[1]为
(3)
式中:Ωz,l、Ωz,h分别为低速侧与高速侧主动轮转速(rad/s);Kv为低速侧与高速侧主动轮转速比,Kv=Ωz,l/Ωz,h;rz为主动轮半径(m)。
在转向过程中,履带接地段在某一瞬时可以看作绕其瞬时转向中心做旋转运动,因此分析内侧、外侧履带接地面中心Cl和Ch的速度,由牵连速度、相对速度及绝对速度的关系可以得到
(4)
由(4)式可以得到
(5)
式中:λ为履带接地段长度与履带中心距之比,λ=L/B;sl、sh分别为低速侧和高速侧履带瞬时转向中心横向相对偏移量,sl=Sl/(L/2),sh=Sh/(L/2)。
由此,可以得到转向半径修正系数及转向角速度的计算式分别为
(6)
根据文献[4]可以得到滑转滑移条件下两侧履带瞬时转向中心横向相对偏移量的方程为
(7)
式中:f为滚动阻力系数;β为履带与地面的摩擦系数。
在一定路面条件和车辆参数下,求解(6)式、(7)式,可以得到各理论转向半径下的转向半径修正系数和转向角速度修正系数。根据以上计算步骤,计算得到转向半径修正系数及转向角速度修正系数与路面条件(用路面滚动阻力系数f与附着系数φ之比进行表征,该值越大,表明路面条件越恶劣,越小则表明路面条件越好)及理论转向半径之间的关系曲面,分别如图2和图3所示。

图2 转向半径修正系数曲面Fig.2 Steering radius correction factor surface
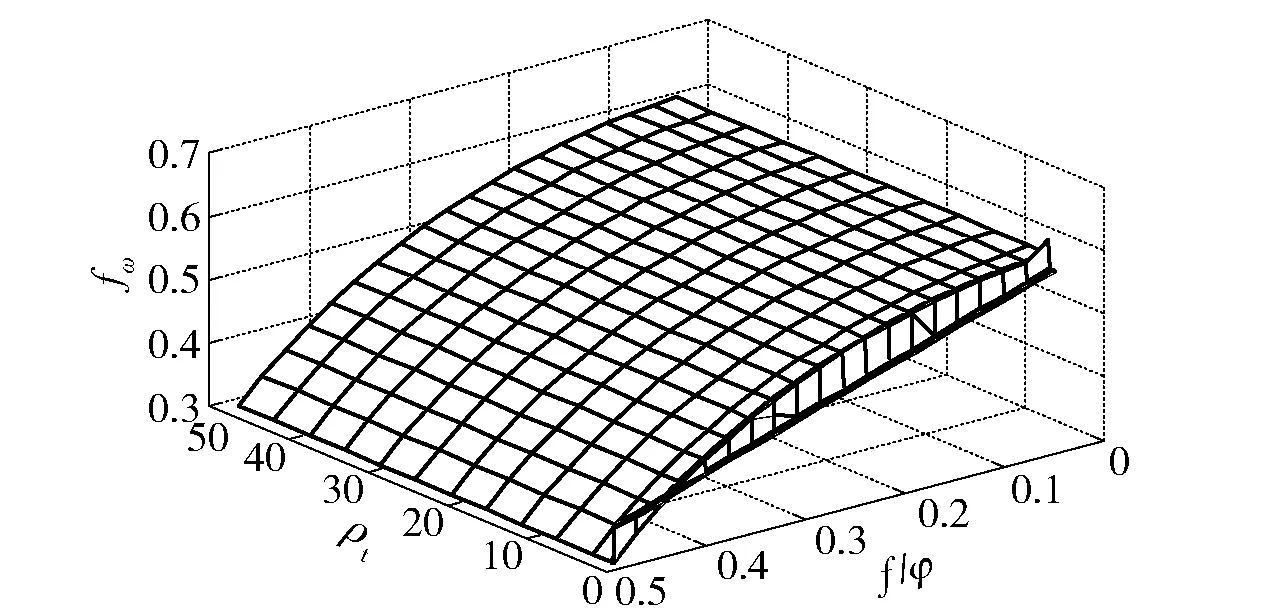
图3 转向角速度修正系数曲面Fig.3 Steering angular velocity correction factor surface
从图2中可以看出:当ρt>0.5时,在一定的路面条件下,转向半径的修正系数大于1.5,且随相对转向半径的增大近似非线性增大;当达到某一个相对转向半径后,修正系数变为恒定值;转向半径修正系数呈非线性增长到转变为定值所对应的相对转向半径值逐渐增大,并且路面条件越好,该定值(即转向半径修正系数最大值)越小。从图3中可以看出:地面条件越差,转向角速度修正系数越小;地面条件较好的情况下,转向角速度修正系数越大,在0.60~0.65范围内,且不随相对转向半径变化而变化。
1.2 双侧电机耦合驱动系统运动学特性
某双侧电机耦合驱动系统简图[13-14]如图4所示。图4中:传动装置由两个驱动电机及其减速排、功率耦合机构及两侧的变速排组成;功率耦合机构由若干行星排构成;ij为电机减速排传动比;kd为耦合机构行星排参数;变速排为两挡,传动比分别为ib1、ib2,将其写成集合的形式为ib={ib1,ib2}。

图4 双侧电机耦合驱动系统简图Fig.4 Structural sketch of dual motor coupling drive transmission
由图4可知:双侧电机输出转速相同时,车辆直线行驶;双侧电机输出转速不同时,车辆差速转向。功率耦合机构是实现双侧电机耦合驱动的关键,它可以将部分或全部转向再生功率由低速侧履带传递至高速侧履带。
相比于液力机械综合传动车辆,电机转速、功率等相关数据较容易获得,因此可以通过驱动电机转速计算两侧主动轮转速,从而获得理论相对转向半径,并利用预先计算得到的转向半径修正系数数据进行查表,得到对应的转向半径修正系数,从而得到车辆实际转向半径,以进行转向运动轨迹控制。
对图4所示双侧电机耦合驱动系统进行运动学分析[15],得到其输入输出转速的变换关系为
(8)
式中:nm,l和nm,h分别为低速侧和高速侧电机转速(r/min);ic为侧传动比。
由(3)式、(8)式,可得车辆理论相对转向半径为
(9)
车辆理论转向角速度为
(10)
常用的转向阻力系数计算公式为尼基金提出的经验公式:
(11)
式中:μmax为坦克做制动转向时的最大阻力系数,该值由试验获得。
(1)式代入(11)式,可以得到转向阻力系数为
(12)
2 考虑履带滑转滑移的转向控制策略
2.1 转向控制策略设计
2.1.1 驾驶操纵信号归一化处理
为方便解算电机转速控制指令,将加速踏板开度信号及方向盘转角信号进行归一化处理[16]。
1)加速踏板开度信号归一化处理:
(13)
式中:Sa为归一化加速踏板开度,0≤Sa≤1;α为实际加速踏板转角;α0为加速踏板空程;αmax为加速踏板最大转角。
2)方向盘转角信号归一化处理:
(14)
式中:Ss为归一化方向盘转角;θ为实际方向盘转角;θ0为方向盘空程;θmax为方向盘最大转角。
2.1.2 转向目标与驾驶操纵信号映射关系定义
利用加速踏板信号、转向盘信号,根据驾驶习惯可定义下述映射关系。
1)目标车速与加速踏板开度的映射关系:
(15)
式中:v*为目标车速(km/h);vmax为最大车速(km/h);nmax为电机最高转速(r/min)。
2)目标相对转向半径与方向盘转角的映射关系:
(16)
式中:ρ*为目标相对转向半径;kib为与挡位及驾驶风格有关的调整系数。
3)目标转向角速度与油门踏板开度及方向盘转角的映射关系:
(17)
式中:ω*为目标转向角速度。
2.1.3 转向控制策略设计
若不考虑履带滑移滑转,则根据运动学分析结果及转向控制目标映射关系,可以得到转向过程电机转速控制指令为
(18)
式中:nm,L和nm,R分别表示不考虑履带滑移滑转时左侧和右侧电机的转速控制指令(r/min)。考虑到履带的滑转滑移,这组目标转速指令并不能保证精确实现转向控制目标,必须针对履带滑转滑移造成的实际转向半径变大来加以修正。
1)当不考虑履带滑动时,要达到目标转向半径ρ*及目标转向角速度ω*,则低速、高速两侧电机转速nm,l和nm,h应当满足:
(19)
2)当考虑履带滑动时,实际转向半径和理论转向半径有如下关系:
ρs=fρρt.
(20)
3)要达到目标转向半径ρ*,则低速、高速两侧电机转速n′m,l和n′m,h应当满足:
(21)
4)当考虑履带滑动时,实际转向角速度和理论转向角速度有如下关系:
ωs=fωωt.
(22)
5)当考虑履带滑动时,要达到实际转向角速度ω*,则低速、高速两侧电机转速n′m,l、n′m,h应当满足:
(23)
由(17)式、(19)式、(21)式,可得考虑履带打滑前后电机转速的相互关系为
(24)
求解(24)式,可以得到n′m,l、n′m,h与nm,l、nm,h的关系为
(25)
令
(26)
实际上,n′m,l、n′m,h为考虑履带滑动后实际需要的低速侧和高速侧电机转速,nm,l、nm,h为不考虑履带滑动时的低速侧和高速侧电机转速。由于修正系数矩阵ξ为对称矩阵,仍然可以利用ξ对左右侧电机转速控制指令进行修正(见(27)式),而不用区分低速侧和高速侧电机:
(27)
式中:n′m,L和n′m,R分别为经过修正后的左侧和右侧电机转速控制指令(r/min)。
进行转速控制指令限幅后,得到转向过程电机转速控制指令为
(28)
2.2 转向控制策略仿真
转向半径修正系数与转向角速度修正系数与理论转向半径之间的关系写入控制程序,在车辆转向过程中,通过电机转速计算车辆理论转向半径,通过查表得到转向半径修正系数与转向角速度修正系数,对电机转速控制指令进行修正,精确实现目标转向半径。
基于MATLAB/Simulink软件建立了电驱动车辆转向工况仿真模型,如图5所示,其中车辆模型为考虑履带打滑的车辆转向模型[17]。

图5 电驱动履带车辆转向仿真模型Fig.5 Steering simulation model of electric drive tracked vehicle
分别采用不考虑履带滑转滑移的转向控制策略和考虑履带滑转滑移的转向控制策略进行仿真,对比分析两种情况的仿真结果。仿真路面设定为水泥路面,控制模型中采用的转向半径修正系数及转向角速度修正系数与理论相对转向半径之间的关系曲线如图6所示。
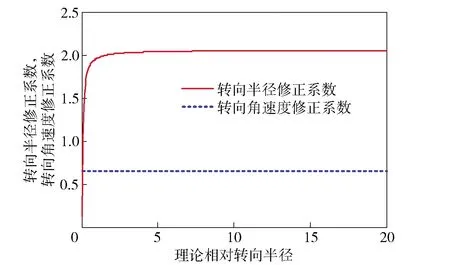
图6 水泥路面转向半径修正系数及转向角速度修正系数Fig.6 Correction factor curves of steering radius and steering angular velocity of tracked vehicle on cement pavement
图7所示为不考虑及考虑履带滑转滑移时的转向控制策略的仿真结果对比。两次仿真采用相同的操纵信号,如图7(a)所示。
由图7可知:考虑履带滑转滑移时,0~100 s两侧电机转速控制指令相同,车辆直驶;21 s左右车速达到8.5 km/h. 不考虑履带滑转滑移时,100~126 s左右两侧驱动电机转速控制指令分别为1 846 r/min及-80 r/min,车辆相对转向半径仿真结果为4.3;126~160 s左右两侧驱动电机转速控制指令分别为1 720 r/min及80 r/min,车辆相对转向半径仿真结果为5.6;160~220 s左右两侧驱动电机转速控制指令分别为1 620 r/min及180 r/min,车辆相对转向半径仿真结果为7.0. 由此可以看出,由于没有考虑转向过程履带打滑的影响,车辆相对转向半径无法达到目标相对转向半径。
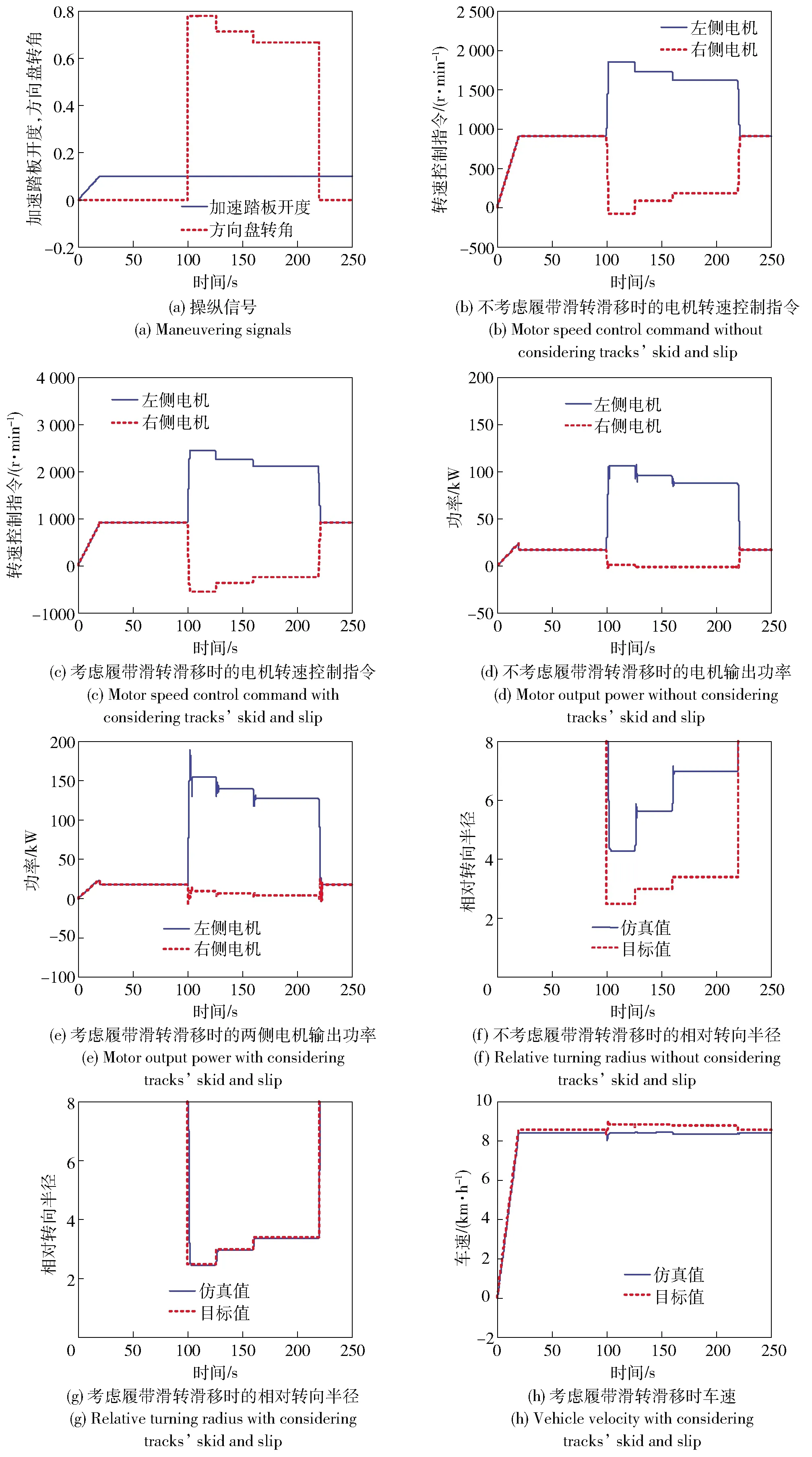
图7 转向控制策略对比仿真结果Fig.7 Simulated results of steering control strategy
考虑履带滑转滑移时:100~126 s左右两侧驱动电机转速控制指令分别为2 420 r/min及-562 r/min,车辆相对转向半径仿真结果为2.5;126~160 s左右两侧驱动电机转速控制指令分别为2 237 r/min及-378 r/min,车辆相对转向半径仿真结果为3;160~220 s左右两侧驱动电机转速控制指令分别为2 100 r/min及-260 r/min,车辆相对转向半径仿真结果为3.4,基本能够达到目标相对转向半径。由此可以看出:考虑履带打滑影响后,两侧电机的目标转速差大于不考虑履带打滑影响时的目标转速差;不考虑履带打滑影响时,由于履带滑转滑移使得实际转向半径大于目标半径,电机输出功率小于考虑履带打滑的转向控制时的输出功率。由于转向半径修正系数与转向角速度修正系数与实际存在一定的偏差,仿真车速与目标车速存在不大于6%的偏差。
3 考虑履带滑转滑移的转向控制试验验证
车辆进行水泥路面转向试验,对考虑履带滑转滑移的转向控制策略进行试验验证。图8所示为转向控制策略试验场地,在图中红色圆圈所示的区域内进行转向,通过总线记录仪对总线网络数据进行采集保存。

图8 转向控制策略试验场地Fig.8 Steering control strategy test site
目标转向半径为48 m,目标相对半径ρ*=18,根据转向控制目标映射规则,方向盘转角归一化值Ss=0.29,即方向盘向右转至右侧最大行程的1/3处左右。由于在驾驶员实际操纵中方向盘不可能与目标值完全吻合,只能尽量接近,并且在试验中要求驾驶员在不出现危险的情况下,将方向盘转至目标位置后便不允许再转动,以验证本文提出的考虑履带滑转滑移的转向控制策略。目标车速定为v*=40 km/h,驾驶员可以根据仪表盘上显示的车速调节油门踏板开度。
3.1 试验1:采用不考虑履带滑转滑移的转向控制策略
图9所示为车辆进行转向试验的结果,其中图9(a)为驾驶员按照要求给出的转向操纵信号,油门踏板开度维持在0.52左右,从13 s开始驾驶员开始缓慢向右转动方向盘,在28 s左右方向盘转至右侧最大行程的1/3处左右。如图9(e)所示,实际相对转向半径约ρs=37,从中可以看出由于未考虑履带滑转滑移的影响,实际半径值约为目标值的2.1倍。
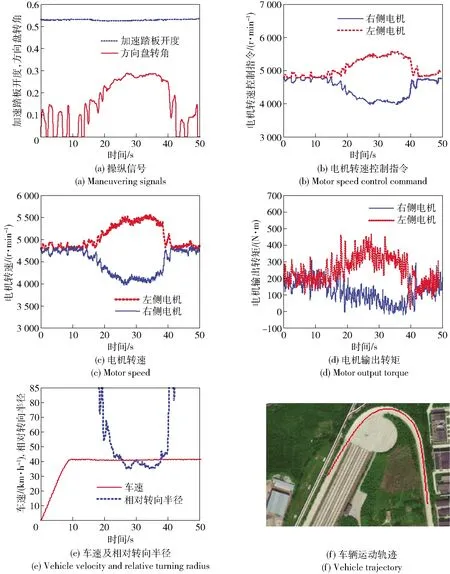
图9 不考虑履带滑转滑移的转向控制策略试验结果Fig.9 Test result of steering control strategy without considering tracks’ skid and slip
3.2 试验2:采用考虑履带滑转滑移的转向控制策略
图10所示为采用考虑履带滑转滑移的转向控制策略进行转向试验的结果。图10(a)为驾驶员按照要求给出的转向操纵信号,油门踏板开度维持在0.55左右,从15 s开始驾驶员开始缓慢向右转动方向盘,在30 s左右方向盘转至右侧最大行程的1/3处左右。电机转速控制指令如图10(b)所示,对比试验1的结果可以看出,由于考虑了履带滑转滑移的影响,两侧电机转速差增大。如图10(e)所示,转向基本稳定时实际相对转向半径约为19,实际半径值基本达到目标值,最终转向半径的控制偏差为5.6%.
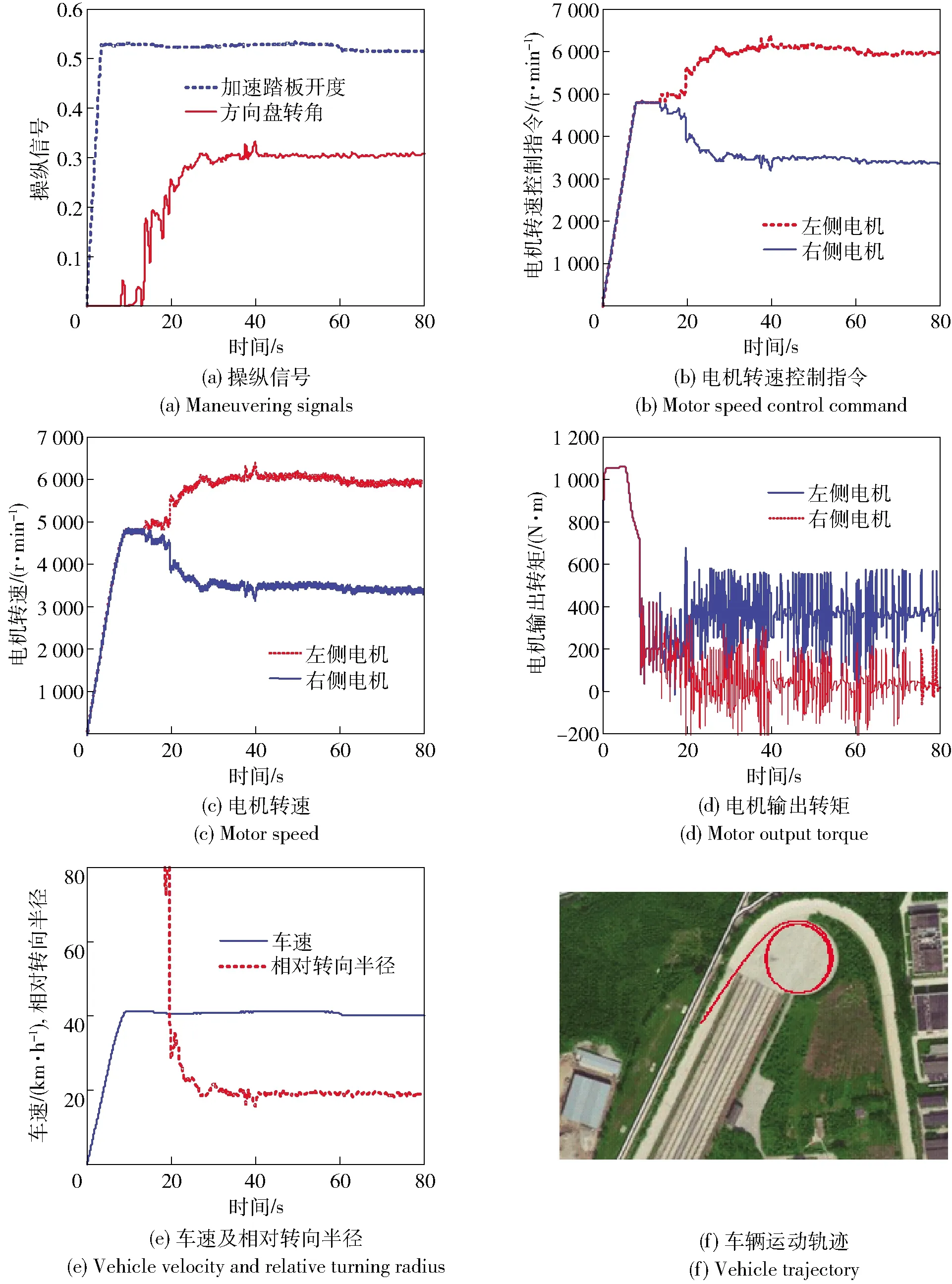
图10 考虑履带滑转滑移的转向控制策略试验结果Fig.10 Test result of steering control strategy with considering tracks’ skid and slip
4 结论
本文履带车辆转向过程滑转滑移特性进行了分析,提出了考虑履带滑转滑移的转向控制策略,进行了电驱动履带车辆转向控制策略仿真及试验验证。通过对比试验结果可以看出:不考虑履带滑转滑移时,车辆实际转向半径为目标转向半径的2倍;采用考虑履带滑转滑移的转向控制策略后,车辆转向半径的控制偏差为5.6%,提高了转向控制的精确度。综上所述,本文提出的考虑履带滑转滑移的转向控制策略具有较好的控制效果。结合路面识别技术,该策略未来可应用于无人履带车辆的转向轨迹精确控制。
