自由设站法在地铁竣工测量中的应用研究

葛 文，井发明，徐长虹，何文峰，李学涛

（1.宁波市测绘和遥感技术研究院，浙江 宁波 315402；2.宁波市阿拉图数字科技有限公司，浙江 宁波 315402）

城市轨道交通作为一种新型的城市交通工具，极大地方便了人们的出行。地铁隧道竣工测量是建设完成后的一项重要基础工作，其竣工资料可为今后的隧道设计、周边施工以及规划督察提供重要的参考信息。如何准确获取隧道的外轮廓线及拱顶、拱底断面线是竣工测量的主要工作[1]。

采用全站仪三维自由设站法测量隧道外轮廓线及断面线时，如何准确获得设站点的三维坐标是整个工作的核心内容，对此，本文尝试将方差分量估计理论和稳健抗差估计理论相结合，提出一种新的抗差Helmert三维自由设站法。相比传统的自由设站法，该方法不仅能够解决不同种类观测值的权值问题，更能抵抗已知点的坐标粗差对设站点坐标解算的影响[2]。最后，根据在某地铁隧道的实践经验，将所建模型应用于竣工测量中[3]，得出了一些有益的 结论。

1 三维自由设站间接平差模型

1.1 三维自由设站

全站仪三维自由设站是指通过观测设站点到两个或两个以上已知点的斜距LS、水平角LH、垂直角LV，利用已知点的坐标、定向角以及观测数据采用间接平差模型处理后，得到设站点的三维空间坐标的测量 方法[4]。

令设站点S的坐标为（XS、YS、ZS），已知点的坐标为（Xi、Yi、Zi），i≥2，设站定向角为A，则观测值方程为：

式中，

根据设站点坐标的改正数与近似坐标，即可推算出设站点的三维坐标。

1.2 基于Helmert方差分量估计的三维自由设站

采用传统的间接平差模型解算设站点三维坐标时，最重要的工作就是各类观测值的赋权，以往人们通常将权值定为单位权，而不考虑不同观测值的类型不同，从而导致平差结果失准，无法达到预期的目的。

距离LS、水平角LH以及垂直角LV属于3种不同种类的观测值，一般情况下全站仪的垂直角观测精度要低于水平角。Helmert方差分量估计法，可以解决多个不同种类观测值定权的问题，进而避免经验定权导致观测值改正数分配不合理的情况。

将三维自由设站的观测值分为3类，即距离观测值L1、水平方向观测值L2、垂直角观测值L3，可得观测值的误差方程为：

为了合理确定3种观测值的权[5]，通常根据全站仪的标称精度确定初始权阵P1、P2、P3。首先进行预平差，然后利用平差后各类观测量的残差平方和，对其验前方差做出估计，重新定权。通过反复计算迭代，使得不同类观测值的单位权中误差趋向一致，从而达到最佳平差效果。

1.3 基于胡贝尔法与Helmert模型的观测值权阵解算

地铁隧道内的已知点往往含有粗差[6]，而Helmert方差分量估计是基于最小二乘原理的一种数学模型，并不具备抵抗粗差的能力。自由设站观测时，已知点的坐标粗差将直接导致观测的角度、距离含有误差，进而设站点的坐标也不精确，粗差同样会使Helmert方差分量估计的权阵出现波动现象，最终导致迭代计算的权阵不收敛。

为解决粗差带来的影响，在Helmert方差分量估计模型的基础上，引入抗差估计理论的胡贝尔法[7]，通过选择ρ函数构造权因子ω，进行迭代平差求解，以此抵抗粗差对方差分量解算的观测值权阵的影响。迭代计算公式为：

式中，c为常系数，通常取c=2σ；v为观测值的改正数；σ为改正数的中误差，由此可得相应的权因子为：

由权因子的方程可知：当所有观测值的改正数都在-c和c之间时，胡贝尔估计其实就是最小二乘估 计[8]；当改正数大于C时，其权因子w与改正数成反比，改正数越大，对应的权因子越小，权也越小，与此相应的观测值对参数估计的影响也越小。

2 地铁隧道竣工测量

规划竣工测量是地铁隧道建设完成后一项重要的基础工作，可为轨道的设计、维护以及周边施工提供重要的基础信息。通过抗差Helmert三维自由设站模型进行地铁隧道竣工测量的主要步骤如下：

1）全站仪架设于隧道轨行区中间位置，观测其到各CPIII（轨道控制点）点的空间距离LS、水平角LH以及垂直角LV，根据全站仪标称精度对三类观测值确定各自的初始权值P1、P2、P3。

2）采用最小二乘法以及上述确定的初始权阵，通过式（4）进行首次平差，计算各观测值的

3）利用Helmert方差分量估计公式（6）计算3种观测值的单位权方差估值，根据式（8）重新调整三类观测值的权。

4）利用胡贝尔法的选权迭代公式（9）重新定权，依次抵抗CPIII点的坐标粗差以及各观测值的偶然误差对平差结果的影响。

7）每隔10～15 m，通过全站仪极坐标法测量隧道同一横断面上的两个点（一般测量隧道断面与轨道道床的相交点），进而计算出隧道中心点坐标和高程，最后，根据隧道壁设计厚度可推算出外轮廓平面坐标和高程。

地铁轨道的道床往往会有一定的倾斜度，如果取左右断面点坐标的平均值作为轨道中心点坐标会导致轨道外轮廓线含有一定的误差，实际计算时，需作一定的改正计算。如图1所示，A、C为隧道某一断面与道床的两个相交点；OX1为垂直于轨道中心线的横轴；断面圆心坐标（XH，YH，ZH）可由A、C两点的坐标通过公式（12）计算所得。

图1 轨道中心点坐标改正计算图

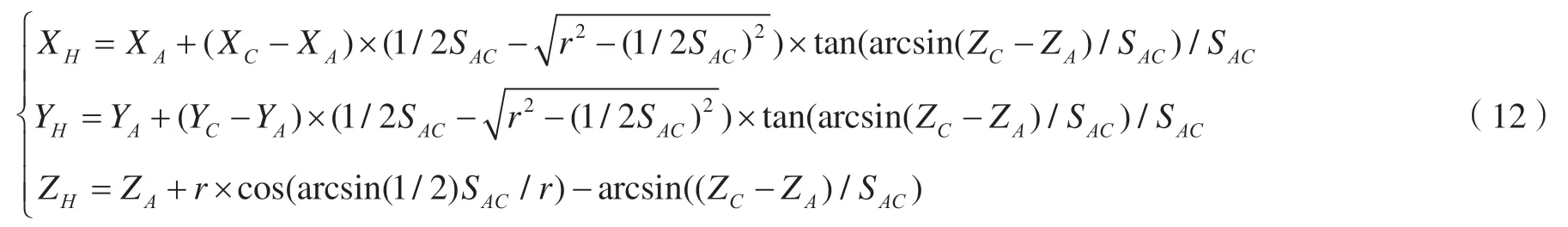
3 案例分析

某市轨道交通四号线计划于2020年底通车，为了充分掌握隧道外轮廓、拱顶及拱底高程信息，需对其进行竣工测绘，即利用已知CPIII控制点，采用三维自由设站法通过观测角度和距离，平差计算获取设站点的平面坐标和高程，进而利用极坐标法获取断面点的坐标，根据公式（12）计算出断面中心点坐标和高程，从而根据设计数据，可推算出隧道外轮廓以及拱顶、拱底坐标。

本文采用某轨道区间的一个断面作为实验数据，以验证抗差Helmert模型的可行性。实际测量时，首先采用两个没有粗差的已知点后视定向获取设站点的 三维坐标为（107020.088，602705.351，-15.464），以此作为设站点坐标的真值。为了方便观测，将全站仪架设于轨道中心，利用两组已知点（每组已知点个数为2个），其中一组已知点坐标含有粗差，一组已知点没有粗差，分别通过最小二乘三维自由设站法、Helmert三维自由设站法以及抗差Helmert三维自由设站法平差计算设站点的三维坐标，如表1所示。

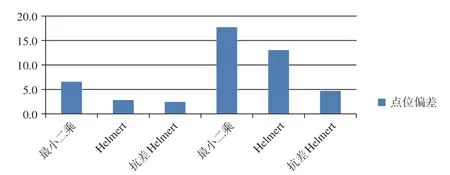
图2 两组已知点获取的设站点的点位误差

表1 两组已知点获取的设站点的点位偏差

由图表数据可知，当已知点坐标没有粗差时，Helmert三维自由设站模型得到的设站点的点位偏差低于最小二乘数学模型所计算出的点位偏差，抗差Helmert三维自由设站模型得到的设站点的点位偏差最小。当已知点的坐标含有粗差时，抗差Helmert三维自由设站数学模型获取的设站点的点位误差最小，且远低于其他两种数学模型，故可知，抗差Helmert数学模型不仅可以抵抗粗差影响且精度最高，Helmert数学模型的精度要优于最小二乘法。

实际地铁隧道竣工时，每隔10～15 m采集一个断面数据，由全站仪自由设站法获取设站点三维坐标后，即可通过极坐标法采集断面上的两个点，由改正公 式（12）可计算出圆心三维坐标，根据设计数据，可得到断面的左右外轮廓以及最高、最低点坐标，采用CAD画弧工具连接相关点，即可得到地铁隧道竣工平面及断面图。

图3 地铁隧道平面竣工图

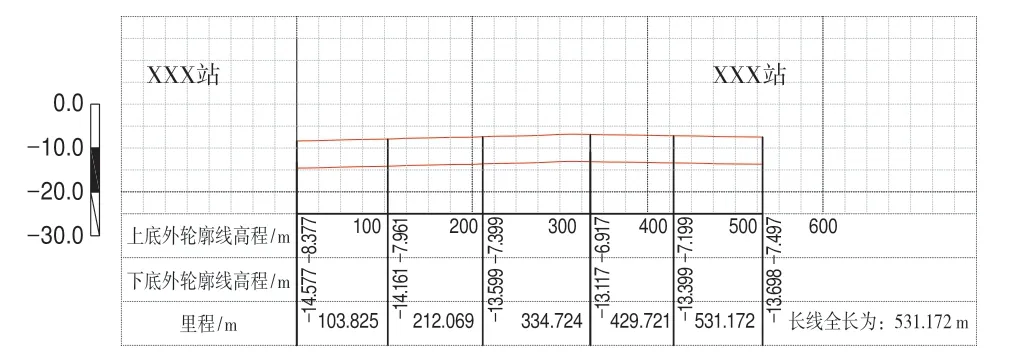
图4 地铁隧道纵断面竣工图

4 结 语

如何确保自由设站点三维坐标的准确性是地铁隧道竣工测量的重中之重，将决定整个竣工成果的精度。本文深入研究了基于抗差Helmert方差分量估计模型，推导了三维自由设站的平差数学模型，并根据实际测量数据，总结出一套坐标改正公式。最后通过地铁隧道某一断面的实测数据进行计算和分析，验证了模型的正确性及可行性，主要研究结果如下：

1）地铁隧道竣工测量是一项重要的基础性工作，通过三维自由设站法获取设站点坐标，然后，利用极坐标法每隔10m左右获取一组断面点，最终由断面点坐标及隧道设计厚度可以获取隧道的外轮廓线以及拱顶、拱底断面线。

2）基于抗差Helmert三维自由设站是一种有效实用的数学模型，不仅可以解决不同种类观测值的定权问题，而且能够抵抗已知点的粗差对设站点坐标解算的影响。

3）地铁隧道横断面上任意不同高度的两个点都可以通过改正公式（12）计算出圆心坐标，从而可以得到隧道的外轮廓、拱顶以及拱底信息，使外业断面点采集工作更加灵活、方便，提高了工作效率。