基于空域分解的雾天图像增强方法
2021-11-14邓守京孙莉莉
王 鹏,齐 洁,张 鑫,邓守京,孙莉莉
(1.大连交通大学 软件学院,辽宁 大连 116028;2.大连口岸物流网有限公司,辽宁 大连 116000)
0 引言
雾与霾是特定气候条件与人类活动相互作用的结果。在空气中悬浮的大量颗粒物会导致拍摄得到的图像质量下降,对计算机视觉应用造成不利影响。对图像进行去雾处理已经成为图像增强领域的主要研究课题之一。
图像去雾技术主要分为两大类:基于图像的去雾方法[1-3]与基于物理模型的场景复原方法[4-6]。芮义斌等人[7]结合雾天图像和场景景深强度关系对交互式图像进行去雾操作,实现了用户对于图像的主观判断先验经验与模型的结合,获得良好的图像去雾效果。禹晶等人[8]设计了一种快速图像去雾算法,利用双边滤波算法合理地估计大气消散函数,进而得到场景反射率,以提高图像的清晰度。为了对高分辨率图像进行去雾,周首峰等人[9]提出将暗通道先验理论与高斯滤波算法结合,对去雾图像进行恢复,优化了算法的计算量。於敏杰等人[10]同时利用不同的算法得到的透射图以及初步去雾图像,得到复原图像,对灰度图像也同样适用。唐宁等人[11]利用双边滤波局部估计雾浓度,间接求取大气耗散函数,最终通过变换的大气散射模型恢复无雾图像。方帅等人[12]设计了针对夜间图像进行去雾的算法,基于信息熵的传输图粗估计的方法,去除不均匀光照影响,提高图像质量。王殿伟等人[13]利用统计截断方法去估计大气光值,并结合暗通道进行粗略估计投射图从而对雾天图像进行去雾。张峥等人[14]提出基于颜色线先验和暗通道先验的遥感图像去雾算法,基于最小二乘的透过率优化方法,通过计算先验可信度权重来加权融合颜色线先验和暗通道先验估计的透过率图,达到去雾效果。王园园等人[15]采用双边滤波优化的方法,对雾天的交通标识进行去雾,效果良好。王锋等人[16]利用二分搜索的方法估计大气光值,利用灰度差获取阈值从而对暗通道进行修正,进行图像去雾。廖干洲等人[17]等人利用深度学习的方法构建模型,获得图像序列,依靠对散射图的估计实现了对图像雾天特征的去处。以上方法均从不同角度对雾天图像进行了复原,但复原的图像仍然存在对比度低、图像过暗或过饱和、色彩失真和细节模糊等问题。
针对上述情况,本文提出了基于空域分解的图像去雾算法,将雾天环境抽象为一种图像噪声,并将按照此设想将雾天图像分解为含有色彩信息的基础层图像以及含有噪声的细节层图像,并分别进行图像处理,最后进行图像层融合,经过实验比较,本文设计的去雾算法得到的复原图像色彩真实,清晰度高,且算法适应性强。
1 算法设计和原理
1.1 算法框架
算法针对雾天的图像,采用利用中值滤波算法,将图像分解为基础层与细节层,再针对色彩空间解耦。基础层图像主要包含色彩信息和亮度信息,采用直方图均衡化,进行亮度和对比度调整;细节层主要包含图像细节信息和噪声信息,解耦后采用非局部均值降噪算法,抑制噪声;将处理后的基层和细节层图像进行融合,最后采用gamma校正,调整图像灰度,得到最终增强图像。算法总框架如图1所示。

图1 基于空域分解的去雾算法总框图Fig.1 General block diagram of defogging algorithm based on spatial decomposition
1.2 雾天模型及图像分解
根据文献[9]的分析,雾天图像符合暗原色先验(Dark Channel Prior,DCP),并且雾天图像适用于图像退化原理,据此建立雾气退化模型:
f(x)=g(x,y)·e-β·d(x)+A(1-e-β·d(x))+n(x,y),
(1)
式中,f(x)为雾天图像;g(x,y)为真实图像;A为大气光;β为空气的散射系数;d(x)为场景深度;n(x,y)为噪声信息。
借鉴文献[18]的双域图像处理思想,雾天图像经中值滤波器分解为包含色彩信息的基础层图像和包含噪声信息的细节层图像。雾气在图像中表现为噪声特征,主要集中在细节层图像中。
根据上述分析,真实图像g(x,y)可由基础层图像gbase和细节层图像gdetail融合得到,如式(2)所示,结合式(2),将式(1)进行变形得到式(3):
g(x,y)=gdetail(x,y)+gbase(x,y),
(2)
f(x)=[gdetail(x,y)·e-β·d(x)+A(1-e-β·d(x))]+
gbase(x,y)·e-β·d(x)+n(x,y)。
(3)
根据分层强化的原理,将式(3)进一步变形得到:
式中,fdetail(x,y),fbase(x,y)为雾天图像的细节层图像和基础层图像;gdetail(x,y),gbase(x,y)为真实图像的细节层图像和基础层图像;fdetail(x,y)包含gdetail(x,y)以及雾气图像和噪声信息;fbase(x,y)主要由gbase(x,y)构成。
雾天图像经中值滤波处理得到基础层图像,如式(4)所示,并与其进行差值运算得到细节层图像,如式(5)所示:
fbase=Med(x,y)×f(x,y),
(4)
fdetail=f(x,y)-Med(x,y)×f(x,y),
(5)
式中,f(x,y)为雾天图像;fbase为基础层图像;fdetail为细节层图像;Med(x,y)为中值滤波,其原理如式(6)所示。
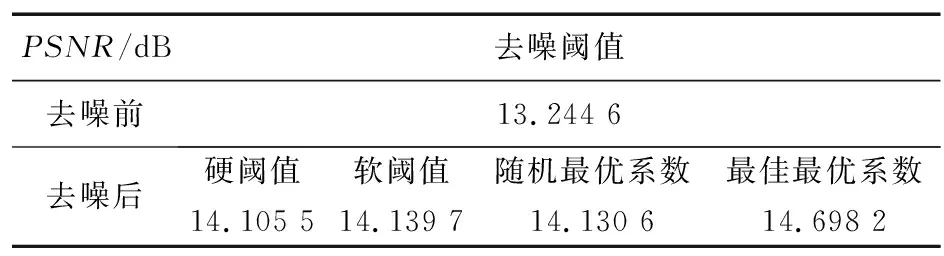
假设x1,x2,…,xn表示n个随机输入变量,按值大小升序排列为xi1 (6) 雾天图像f(x,y)经过中值滤波器分解,得到基础层图像fbase和细节层图像fdetail。为了验证中值滤波器对图像分离效果以及分解后细节层噪声含量,对图像Table进行分解,如图2所示,中值滤波卷积核大小为5×5,添加噪声的标准差为0.05。 (a) 原图 (b) 基础层 (c) 细节层 (d) 噪声原图 (e) 噪声基础层 (f) 噪声细节层图2 Table原图及噪声图像分解效果图Fig.2 Original Table image and noise image decomposition effect 通过对分解后的细节层图像分析可知,图2(b)与图2(e)差别很小,噪声信息基本集中在细节层中,经过计算,图2(d)噪声原图的噪声标准差为0.020,图2(f)噪声细节层的噪声方差为0.019。空域分解使得雾气噪声全部分解在细节层,避免了进行去雾处理时,对基础层图像色彩结构的干扰,通过分别对基础层图像和细节层图像的增强,可同步实现图像去雾与对比度的提高。 为了改善基础层图像fbase对比度,平衡色彩结构,还原图像本身色彩,选择具有均衡功能的直方均衡化算法对基础层图像fbase进行校正。 假设基础层图像fbase中的像素为N,图像的灰度级数为L,灰度级空间为[0,L-1],用nk表示k级灰度(第k个灰度级,像素值为k)在图像内的像素点个数,那么该图像中的灰度级rk(第k个灰度级)出现的概率为: 根据灰度级概率,对其进行均衡化处理: 直方图均衡化使图像色彩更加均衡,外观更清晰,更加易于处理。使用直方图均衡化算法增强基础层图像fbase,步骤如下: (2) 统计直方图,进行像素统计,形成直方图; (3) 将累计直方图进行区间转换,均衡化处理; 雾天图像含有大量噪声,主要是由图像的采集过程以及大气中颗粒折射、散射现象产生,若不加以抑制,会对最终图像造成影响。为了更好地分离、除去噪声,选择具有分辨性高的小波变换进行噪声和雾气抑制。 1.4.1 小波阈值去噪原理 图像为二维信号,用二元函数f(x,y)∈L2(R2),ψ(x,y)表示,可以对其进行二维小波变换和多辨分析,设f(x,y)∈L2(R2),ψ(x,y)满足式(7): (7) 则称积分,如式(8)所示,为f(x,y)的二维连续小波变换: (8) 图像小波阈值去噪的基本思想是将图像转变为二维信号,如式(7)进行小波变换,并按照小波系数进行分类,同时设置一个临界阈值λ,若小波系数小于阈值λ,认为该系数主要由噪声引起,去除这部分系数;若小波系数大于阈值λ,则认为此系数主要是由信号引起,保留这部分系数,然后对处理后的小波系数进行小波逆变换得到去噪后的信号。 1.4.2 改进的自适应小波阈值去噪 首先,为了使阈值和噪声的大小成某种函数关系,取小波系数在各个尺度下绝对值的中值,然后将该中值除以常数0.674 5作为该尺度下小波系数中噪声强度的估计,即: (9) 式中,j为小波分解的尺度;dj(k)为小波分解系数;Med为中值运算。则全局阈值为: (10) 式中,M,N是图像的尺度。 其次,基于小波阈值降噪原理,对阈值函数进行优化,并添加最优系数α,α∈[0,1],用于满足自适应小波阈值去噪,即: (11) 式中,ω为小波系数;λ为临界阈值;α为最优系数。优化后的阈值函数当α=0时为硬阈值,α=1时为软阈值,α在0~100间为区间阈值。实现了从硬阈值到软阈值的平缓过渡,既可以保留边缘等局部特征,处理结果也会更加自然。 最后,为了确定最优系数α的数值,使用图像去噪的评价标准峰值信噪比(PSNR)[16]: (12) 假设PSNR与最优系数α之间存在某种函数关系,将这个函数成为∂(x),函数关系为: PSNR=∂(α)。 (13) 为了使得图像抑制噪声与雾气的效果达到最佳,在最优系数α的范围内,PSNR为最大值,对应的最优系数α为最佳。 改进的自适应小波阈值去噪算法步骤如下: (2) 设置初始最优系数为0.01,提取各层高频系数,并按照式(12)计算噪声方差; (4) 用处理后各分量进行小波图像重构; (14) 为了最后融合的图像色彩更加真实,细节更加突出,设计了gamma校正,对最终增强图像fI进行处理。 gamma校正(幂律变换)是一种重要的非线性变换,是对输入图像灰度值进行指数变换,进而校正亮度偏差,通常应用于扩展暗调的细节。一般情况下,当gamma校正的值大于1时,图像的高光部分被压缩而暗调部分被扩展;当gamma校正的值小于1时,图像的高光部分被扩展而暗调部分被压缩,在最简单的情况下,gamma校正定义为: s=crγ, (15) 式中,γ为gamma值;r为灰度值;c为系数;s为变换结果。 为了验证算法的效果,开展改进的小波阈值去噪实验与雾天图像去雾对比实验进行验证,实验图片选择参考文献[8-10]展示图像以及雾天图像。 实验环境采用Intel i5处理器、Windows7系统、内存大小为4 GB的计算机,使用编程语言为Python,使用的编程软件为Pycharm,函数库opencv、numpy和math等。 为了验证改进的小波阈值去噪算法性能,选择硬阈值去噪算法、软阈值去噪算法、随机设置最优系数阈值算法以及本文最优系数阈值去噪算法进行同步实验对比,选择图像进行人为添加噪声,噪声均值为0,方差分别为0.02,0.04,0.06,进行去噪实验,去噪实验结果如图3~图5所示。 (a) 硬阈值去噪后的图像 (b) 软阈值去噪后的图像 (c) 随机最优系数去噪后的图像 (d) 最优系数去噪后的图像图3 方差为0.02,各算法去噪效果Fig.3 Denoising effect of each algorithm when the variance is 0.02 (a) 硬阈值去噪后的图像 (b) 软阈值去噪后的图像 (c) 随机最优系数去噪后的图像 (d) 最优系数去噪后的图像图4 方差为0.04,各算法去噪效果Fig.4 Denoising effect of each algorithm when the variance is 0.04 (a) 硬阈值去噪后的图像 (b) 软阈值去噪后的图像 (c) 随机最优系数去噪后的图像 (d) 最优系数去噪后的图像图5 方差为0.06,各算法去噪效果Fig.5 Denoising effect of each algorithm when the variance is 0.06 图6~图8是不同噪声方差下,PSNR与最优系数变化曲线,可以看出,在最优系数范围内,PSNR随最优系数变化进行调整,并可以取到最值。 图6 噪声方差0.02,PSNR随最优系数的变换曲线Fig.6 Transformation curve of PSNR with optimal coefficient when noise variance is 0.02 图7 噪声方差0.04,PSNR随最优系数的变换曲线Fig.7 Transformation curve of PSNR with optimal coefficient when noise variance is 0.04 图8 噪声方差0.06,PSNR随最优系数的变换曲线Fig.8 Transformation curve of PSNR with optimal coefficient when noise variance is 0.06 由表1~表3的不同程度噪声下图像去噪前后峰值信噪比可以看出,经过小波阈值去噪后,PSNR有了明显提高,设计的小波阈值去噪方法对具有高斯白噪声的图像去噪具有较好的效果。同时,比较表中硬阈值、软阈值、随机最佳系数阈值和最佳系数阈值可以得出以下结论:软阈值相对于硬阈值具有更好的图像去噪效果;设计的优化阈值取得了最好的效果,优化阈值融合了硬阈值和软阈值的优点,表现出更好的图像去噪能力。 表1 噪声0.02,不同阈值去噪前后的PSNRTab.1 PSNR before and after noise removal with different thresholds when noise variance is 0.02 表2 噪声0.04,不同阈值去噪前后的PSNRTab.2 PSNR before and after noise removal with different thresholds when noise variance is 0.04 表3 噪声0.06,不同阈值去噪前后的PSNRTab.3 PSNR before and after noise removal with different thresholds when noise variance is 0.06 为了更好地评价算法的性能指标,对比算法的优劣性,选取雾天图像行算法实验,将本文算法与文献[10]的色彩空间的直方图均衡化算法(HE)、文献[11]的改进基于暗通道先验图像去雾算法(DCP)、文献[12]改进的多尺度Retinex算法(MSR)以及文献[13]的结合自动色阶的暗通道去雾算法(AL)进行主观视觉效果上的比较;客观上通过等客观评价指标作为衡量标准,对测试集中雾天图像和经各算法增强后的图像进行质量对比评价。 2.2.1 图像视觉评价 本文选用了雾天图像进行实验,因文章篇幅有限,本文选取3组环境亮度不同,雾天状态存在差异的图片作为评价展示,分别是village,expressway,trail。 第1组的实验结果如图9所示。 (a) 原图 (b) HE (c)DCP (d) MSR (e) AL (f) Ours图9 Village图像去雾算法效果对比Fig.9 Comparison of village image defogging algorithms 图9(a)原图为原始图片,图像因雾气原因,清晰度低,图像中景深小,物体模糊,远处无法看清,图像中的指示牌和车辆标识都无法看清。经过图9(b)HE增强算法后,图像亮度增加,纹理细节突出,但是景深不够且清晰度不够,视觉效果较差;图9(c)DCP增强算法与HE增强算法相比对比度再度有所提升,图像的信息比较明显,近处的物体较为明显,但是整体亮度有所下降失真,图像偏暗。经图9(d) MSR算法处理后的图像亮度适中,明暗差有所减小,但抑制雾气效果不好,清晰度较低;图9(e) AL算法增强后,图像的景深有所提高,但近处颜色失真,无法判断颜色与景物;图9(f) Ours为本文设计算法增强后的图像,近处的指示牌和车的车牌部位信息清晰可见,可辨别,车道线和边花草更加清楚,颜色更加真实,亮度、对比度相比原图有效提升,信息也有很好的显示,并且细节清晰。 第2组的实验结果如图10所示。 (a) 原图 (b) HE (c)DCP (d) MSR (e) AL (f) Ours图10 Expressway图像去雾算法效果对比Fig.10 Comparison of expressway image defogging algorithms 图10(a)原图地理位置为高速公路,车牌信息因为雾气遮挡无法看清,更无法识别;经过图10(b)HE增强算法后,亮度改善不明显,且天空区域出现大量噪声,但车牌信息有所凸显,远景中车辆灯光区域出现光晕等噪声;图10(c)DCP增强算法中出现色彩失真,主要集中在天空区域,图像亮度降低,色彩出现混乱提升,视觉效果差,主要原因是由于图像expressway存在大量天空区域,由于算法对天空区域处理存在敏感度低以及暗通道像素值较高的缘故,导致处理结果不理想;经图10(d) MSR处理后的图像亮度、对比度和纹理细节都有明显增强;图10(e) AL算法增强的图像景深相对较大,但是对于近处的景物色彩像素出现堆积,导致近处出现黑色区域,导致色彩失真严重。图10(f) Ours为本文设计算法处理后的图像各项属性均有明显提升,图像细节清晰,车牌部分更加清晰,更加有利于图像的进一步处理。 第3组的实验结果如图11所示。 (a) 原图 (b) HE (c)DCP (d) MSR (e) AL (f) Ours图11 Trail图像去雾算法效果对比Fig.11 Comparison of trail image defogging algorithms 由这一组图片可以很明显感受到算法的增强。图11(a)原图是环山公路,图片信息识别困难,远处人像更无法显示,近处的植物也很模糊;图11(b) HE算法增强的图像,虽然能使整体明亮一些,但是抑制雾气效果不够理想,景深不够;图11(c)DCP视野区域亮度降低,整体偏暗,去雾效果良好,景深较大,需再次对亮度进行增强;图11(d) MSR图像经过算法处理,亮度均有所提升,但图像中左侧树木存在去雾偏差,树木出现虚化,影响整体效果;图11(e)AL算法处理的图像存在曝光区域,中间天空区域亮度过高,导致亮度出现失衡;图11(f) Ours为本文设计算法呈现的效果较为自然,细节信息明显,右侧水坑清晰可见,远处人影也可分辨清楚,层次感分明。 本文设计算法针对不同类型的雾天图像均能挥发稳定的功效,增强后的图片十分自然,并且细节效果展示充分。 2.2.2 图像属性评价 为了进一步验证所提出算法的性能,客观地评价经算法处理后的图像质量,本文采用5种常见的图像属性作为评价标准[16],对经过9种增强算法处理的图像进行评价如表4~表6所示。 由表4~表6的数据综合分析可以看出,本文算法在图像信息量以及清晰度方面优于其他几种算法,在亮度以及对比度方面基本可以保持在同一水平。为了进一步对比改进的算法,设置算法Ours-1,该算法采用与Our一样的算法结构,在对细节层进行降噪处理是采用硬阈值的小波去噪算法。 表4 village增强算法评价数据Tab.4 Evaluation data of village enhancement algorithm 表5 expressway增强算法评价数据Tab.5 Evaluation data of expressway enhancement algorithm 表6 trail增强算法评价数据Tab.6 Evaluation data of trail enhancement algorithm 本文提出了一种基于空域分解的图像去雾算法,针对有雾图像进行处理。通过对图像进行分解,将含有雾天的图像转换到细节层图像,并通过去噪算法加以优化,实现了图像色彩和噪声的同步处理,利用直方图均衡化算法,使得算法在保证图像质量的情况下同时提升了亮度、清晰度和对比度。经本文算法处理后的图像颜色自然,画面质量高,图像细节信息丰富。与其他去雾算法相比,本文算法在去除噪声、恢复色彩方面有了明显提升,经处理的图像各项属性均有所提升,图像颜色自然,画面质量高,图像细节信息丰富。对于含有大面积天空区域的雾天图像使用算法后也有一定效果,但仍显不足,该类图像也是今后主要攻克的问题。




1.3 基础层直方图均衡化
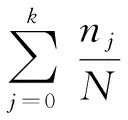

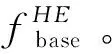
1.4 细节层改进的自适应小波阈值去噪



1.5 图像融合及gamma校正
2 实验结果与分析
2.1 改进的小波阈值去噪实验













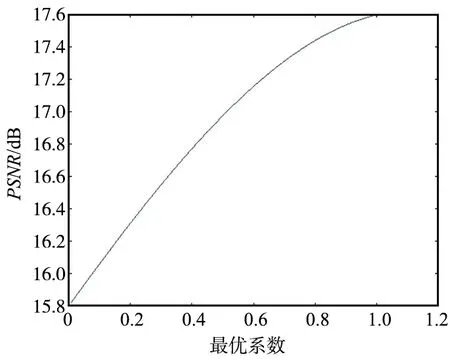



2.2 雾天图像去雾对比实验





















3 结束语
