基于时延估计的空间机器人无模型姿态解耦控制

2021-11-14刘金国

宇航学报 2021年9期

张鑫，刘金国

(1. 中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016；2.中国科学院机器人与智能制造创新研究院，沈阳 110169)

0 引言

空间机器人系统拥有卫星的机动能力和机械臂操控能力[1]，在空间目标捕获[2-4]、在轨更换核心部件[5]及在轨建造等任务中起着重要作用。不同于固定基座机器人，空间机器人的浮游基体会导致动力学同步耦合问题，即机械臂的运动将影响基体的位置和姿态，同时基体的耦合运动将反作用影响机械臂的操作精度[6]。由于动力学耦合将引起基体姿态失控或导致机械臂与抓捕目标发生碰撞[2]，因此补偿或抵消动力学耦合是空间机器人领域的一个重点关注问题。从当前文献分析，学者主要是从运动规划和解耦(或协调)控制两方面来解决此问题。

对于运动规划方法的研究，主要集中于自由漂浮空间机器人[7]，即仅机械臂可控，基体位置和姿态不受控制。由于自由漂浮空间机器人是一个非完整约束系统，因此它的系统状态不仅与关节角度值变化有关，而且与关节速度轨迹也有关[8]。同时，不同于固定式机器人，自由漂浮空间机器人的奇异性为动力学奇异性，即奇异性不仅与运动学参数有关，而且与动力学参数也有关[9]。早期，Torres等提出扰动和增强扰动图的方法，旨在关节空间中找到引起基座扰动较小的可行轨迹[10]。Nakamura等提出了一种双向规划方法，该方法利用非完整的冗余特性来同时规划末端执行器和基体[11]。Sone等提出了反作用零空间(Reaction null-space, RNS)方法，该方法将基体运动映射到机械臂的零空间中，因此该方法要求机械臂具有运动学冗余自由度[12]。尽管，RNS方法已在ETS-VII卫星上得到了验证[13]，然而动力学奇异性限制了RNS方法的应用。此外，Huang等提出一种面向双臂空间机器人的动态平衡方法，以减小基体干扰，其本质原理也是利用机械臂的运动学冗余特性[14]。文献[15]提出一种基于组合函数的笛卡尔轨迹规划方法，利用混沌粒子群算法优化轨迹，该方法可同时兼顾空间机器人的动力学奇异性、基体姿态扰动及运动时间问题。类似的，一些学者利用差分进化[16]和快速搜索树[17]，来规划扰动最小或无扰轨迹，但此类方法需要迭代计算，效率往往不高。

在解耦控制方面，一些学者提出将空间机器人系统分为两个子系统，即机械臂控制系统和基体控制系统。Longman等[18]采用逆动力学分析方法来获得耦合作用力，并将耦合作用力作为前馈输入到控制系统中。事实上，耦合表现为基体与机械臂之间的作用力与反作用力，可采用牛顿-欧拉递推方法计算基体与机械臂之间的内部作用力/力矩[19]。Oda等[20]提出用角动量守恒方法来估计基体的角动量，同样也是采用前馈—反馈的控制方法实现补偿基体的反作用。冯骁等[21]采用角动量前馈补偿和逆动力学算法设计了适用于多臂空间机器人捕获目标的协调控制器，其中逆动力学算法本质上为基于模型的计算力矩方法。实际上，空间机器人为多输入多输出(Multi-input multi-output, MIMO)系统，一些学者设计了基于整体模型的控制器来实现基体与机械臂之间的协调控制。Jayakody等[22]提出一种基于虚拟控制输入的方法实现系统的解耦，并提出一种基于自适应变结构的控制方法，实现基体与机械臂的协调控制。进一步，Shi等[23]提出一种基于对角化方法将MIMO系统转变为单输入单输出(Single-input single-output, SISO)系统，同时分别采用三种方法：计算力矩法、滑模控制、模型预测控制来实现对整个系统解耦。Kumar等采用前馈神经网络来学习空间机器人系统的动力学，并设计一个基于神经网络的自适应控制器，以实现对基体与机械臂的协调控制[24]。然而，以上基于模型的控制方法[18-24]，计算动力学模型参数将耗费大量计算资源。

综上所述，运动规划方法主要面向自由漂浮空间机器人，尽管反作用零空间方法可以在实时规划场景应用，但它需要零空间的维度足够大才能保证产生无反作用的关节轨迹。轨迹优化方法的本质为离线迭代优化方法，它通常需要足够的时间去获得满意的结果。总体来说，运动规划方法往往偏重于自由漂浮空间机器人的理论研究。相比而言，解耦控制方法主要面向自由飞行空间机器人，此类方法更偏重于实际场景中应用，当前运动控制算法主要的挑战在于星载计算机的运算能力有限，导致复杂的控制算法将不适用于星载计算机实时解耦控制。

不同于基于模型的解耦控制方法，本文面向空间机器人的姿态耦合问题，提出一种基于时延估计(Time-delay estimation, TDE)的解耦控制方法，实现对空间机器人系统动力学的高效解耦。通过引入常数对角阵对动力学模型进行改造，将新模型划分为：线性项和新非线性项。对于新非线性项，采用TDE来估计，该方法利用模型前一时刻的观测信息和控制输入来估计当前时刻系统的非线性动力学项。TDE方法估计非线性项不需要计算模型参数，为无模型估计算法，且计算效率高。

1 系统建模

图1所示为空间机器人系统示意图，空间机器人系统包括两部分：基体和机械臂。其中，基体具有6个自由度，机械臂具有n个自由度。图1中相关符号定义，见表1。这里在不特别指明的情况下，各符号默认定义在惯性坐标系中。

表1 符号定义Table 1 Symbol definitions

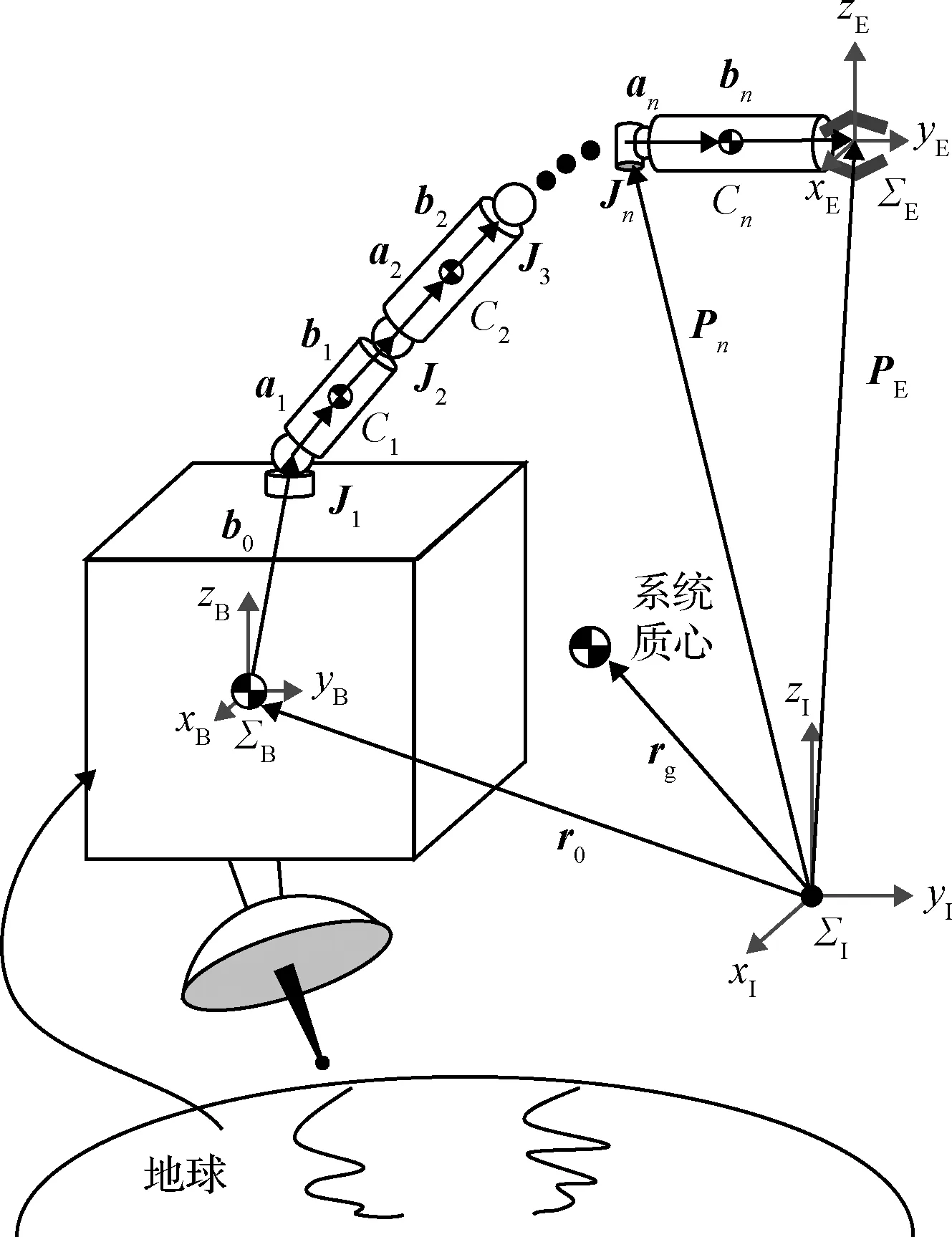
图1 空间机器人系统：卫星—机械臂系统Fig.1 Space robot system: satellite-manipulator system

此外，系统的建模与控制基于以下两点假设：

1)空间机器人工作于微重力环境，即：g≈0。

2)空间机器人系统配备高功率动量轮或反作用飞轮，可提供足够的动力来调整基体姿态。

1.1 姿态运动学

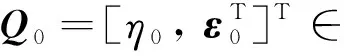
(1)

(2)

式中：ε0=[ε0x,ε0y,ε0z]T∈3为四元数的向量部分，η0为四元数的标量部分，它们满足如下限制条件：故Q0仅具有3个独立变量。此外，符号表示反对称矩阵，对于向量定义为：

(3)

1.2 系统动力学

采用复合刚体动力学建模方法，建立空间机器人动力学方程，名义模型可表示为：

(4)

式中：H∈(n+6)×(n+6)为系统惯性矩阵，HB∈6×6和HM∈n×n为对应基体和机械臂的惯性矩阵，HBM∈n×6为基体与机械臂之间的耦合惯性矩阵，c∈n+6为系统的速度独立非线性项，cB∈6×6和cM∈n×n为基体和机械臂的速度独立项矩阵，cBM∈6×n和cMB∈n×6为速度独立项耦合矩阵，F∈n+6为系统驱动力项，6为作用于基体的力和力矩，τM=[τ1,…,τn]T∈n为机械臂关节力矩项，θ=[θ1,…,θn]T∈n为机械臂关节角向量，6为基体的广义加速度项，n+6为系统的广义位置项，n+6和n+6为系统的速度和加速度项。

复合刚体动力学建模方法是一种高效的建模方法，它综合了惯性矩阵方法和牛顿—欧拉迭代方法，通过系统动能来推导系统的惯性矩阵，通过牛顿—欧拉逆动力学推导系统的非线性独立项。具体建模过程如下：

1)惯性矩阵

空间机器人处于微重力环境，不具有重力势能，系统能量主要体现为系统动能，表示为：

(5)

式中：mi和Ii∈3×3为连杆i的质量和惯性张量，ωi∈3和vi∈3为连杆i的角速度向量和质心线速度向量，当i=0表示基体。进一步，式(5)可转化为：

(6)

因此，可得到系统的惯性矩阵H(ρ)。

2)速度独立非线性项

由于速度独立非线性项与系统加速度无关，故可以通过牛顿—欧拉逆动力迭代算法求解此项[25]。牛顿—欧拉算法包括两步：第一步，速度和加速度正向推导，其中(i=1,2,…,n)；第二步，力和力矩逆向推导，其中(i=n-1,n-2,…,0)。

(7)

(8)

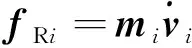
(9)

式中：FNE(·)表示牛顿—欧拉递推方程函数。进一步，可将式(4)简化为：

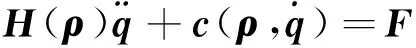
(10)

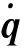
(11)

(12)

(13)

进一步，将式(11)和(13)代入式(10)中，同时，左乘J-T以保证变换后的惯性矩阵为正定矩阵，得到：

(14)

其中:

HS(ρ)=J-TH(ρ)J-1

(15)

(16)

(17)

因此，式(14)为系统动力学的名义模型。

然而，实际中需要考虑扰动及不确定性的影响，假设扰动和不确定性有界，因此实际模型可表示为：

(18)

式中：扰动项记为：fd=[fd0x,fd0y,fd0z,td0x,td0y,td0z,ti,…,t6]T∈n+6，且各元素满足有界性；不确定项记为：且fu=[fu1,…,fui,…,fu(n+6)]T∈n+6，同时各元素满足有界性。

2 动力学解耦分析

2.1 系统耦合分析

如图2所示，对于单臂空间机器人，基—臂耦合体现在机械臂反作用于基体上的力和力矩，直观地表现为关节1处的作用力及力矩。进一步，对式(4)进行分解可得两个子系统：

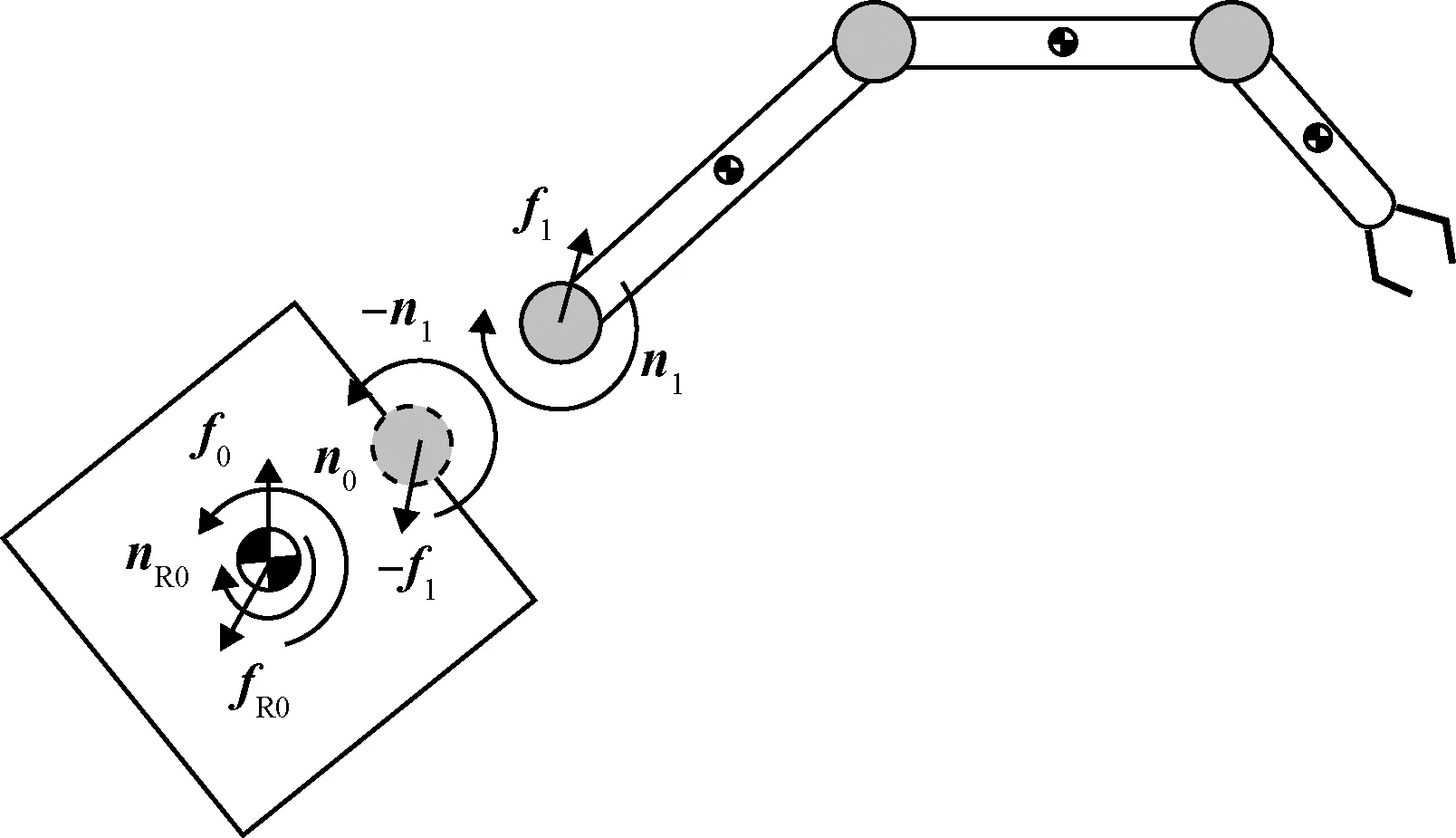
图2 机械臂与基体的耦合作用Fig.2 Coupling action between the manipulator and the base

(19)

2.2 控制输入变换

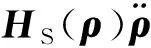
对于基体姿态受控而位置不受控的空间机器人，需要对控制输入进行变换：

(20)

式中：FDS=DSFS=[0, 0, 0,FDS4,…,FDS(n+6)]T∈n+6为变换后的空间机器人基体驱动力项，DS为控制输入变换矩阵，表示为：

(21)

3 控制器设计

3.1 基于模型解耦控制

计算力矩控制(Computed torque control, CTC)为经典的基于模型解耦控制方法，通过在线计算系统的非线性项和惯性矩阵，并通过PD控制补偿误差，实现系统完全解耦与线性化。

如图3所示，CTC控制律，表示为：

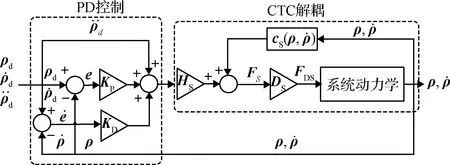
图3 经典的CTC解耦控制Fig.3 Classical CTC decoupling control

FS=HSuCTC+cS

(22)

(23)

式中：KP和KD∈(n+6)×(n+6)，分别为比例增益矩阵和微分增益矩阵；e和n+6为状态误差及其导数。将式(22)代入式(14)中，可得完全解耦的线性定常系统：

(24)

3.2 无模型解耦控制

当前，最常见的无模型控制器，为智能PID控制器[27]，但PID控制器大多适应于SISO系统，同时参数整定也需要设定一些智能规则。空间机器人为连续变量MIMO系统，本小节采用TDE控制实现无模型解耦控制，TDE是上世纪90年代由Hisa等提出，早期主要应用于传统工业机器人[28]。TDE的基本思想是利用模型前一时刻的观测信息和控制输入，来在线估计当前时刻连续变量系统的未知动态，实现对系统非线性项的补偿。

对于TDE控制，第一步，通过引入常数对角阵，对系统动力学模型进行变换。第二步，将系统视为黑箱系统，通过综合上一时刻输出和输入信息，来估计系统的动态。因此，它不需要在线计算非线性项和惯性矩阵，为无模型解耦控制方法。如图4所示为TDE解耦控制原理图。

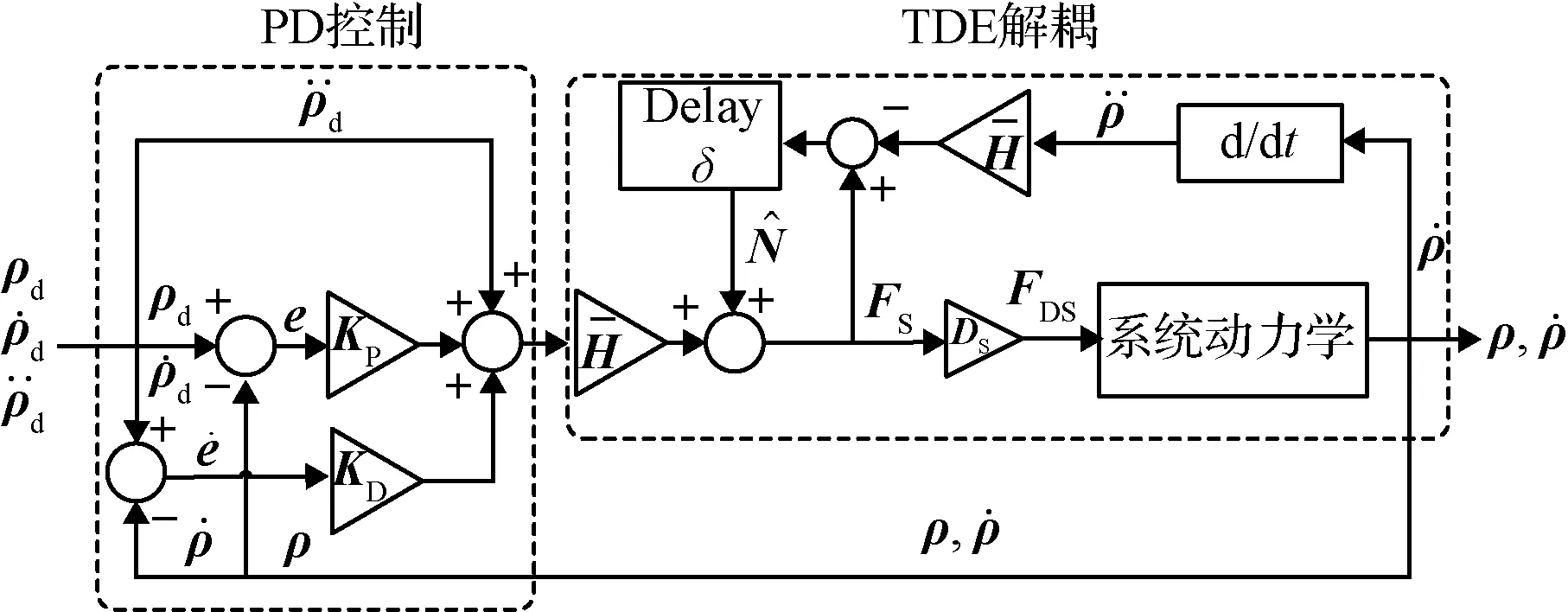
图4 TDE解耦控制Fig.4 TDE decoupling control

对于式(20)进行变换，有：

(25)

(26)

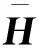
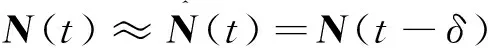
(27)

式中：N(t-δ)为TDE项，表示对N(t)的估计，δ为系统采样间隔。若想保证TDE的精准性，需要保证δ足够小[28]。根据式(25)，可知：

(28)

进一步，TDE控制律可表示为：

(29)

(30)

将式(29)和(28)，代入式(25)中，可以得到：

(31)

式中：设ε(t)=N(t)-N(t-δ)，表示TDE误差。

进一步，将式(30)代入式(31)中，可得：

(32)

对于TDE闭环控制系统稳定性，等同于证明e(t)渐近收敛，也就是证明ε(t)渐近有界的。考虑到空间机器人为连续非线性系统，ε(t)满足有界性。关于ε(t)渐近有界性证明，详见文献[25, 28]。

3.3 定性对比分析

TDE解耦与CTC解耦原理都是通过补偿系统非线性项来实现解耦，但在技术途径上差异很大。具体体现为：CTC需要实时计算系统参数cS和HS，来实现系统的解耦与线性化；而TDE控制采用模型变换和在线估计的强解耦方法，其解耦原理简单，易于应用。此外，考虑到卫星所携带星载计算机的计算能力有限，对于基于模型的控制器将耗费大量的计算资源。不同于基于模型的CTC控制方法，基于TDE的无模型控制器不需要实时计算模型参数，计算效率更高，更具应用前景。

4 数值校验

本节仿真以在轨观测任务为背景，控制目标是保证机械臂的精准运动并维持基体姿态稳定。图5所示为空间机器人系统模型，本节采用3个仿真案例，分别为：基于名义模型、考虑外界扰动、考虑参数不确定性，对比验证所提出的无模型解耦控制方法的有效性。

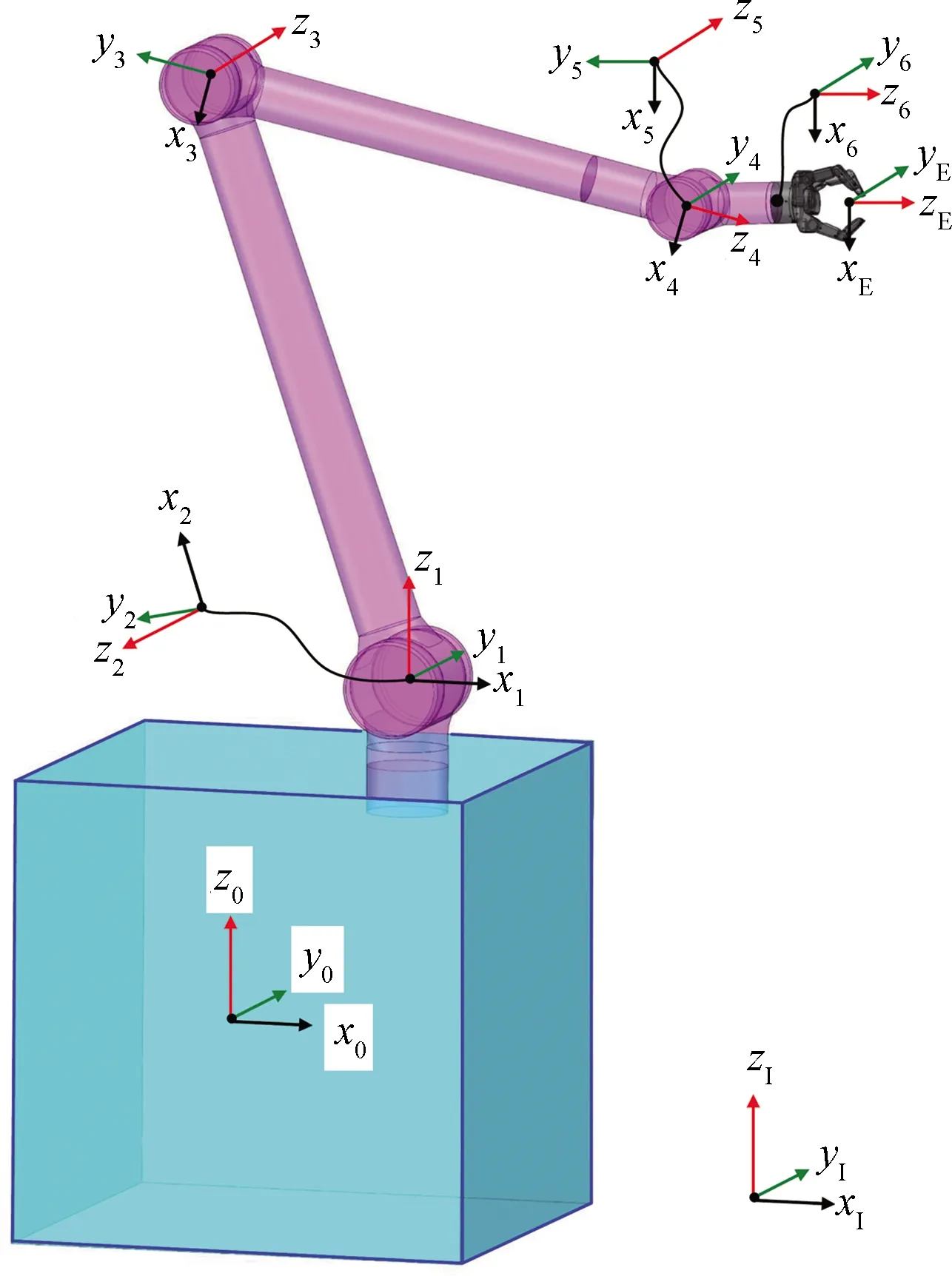
图5 空间机器人模型Fig.5 Space robot model

图6所示为空间机器人运动过程，具体包含两个步骤：1)机械臂从初始构型到中间构型;2)从中间构型到终端构型。

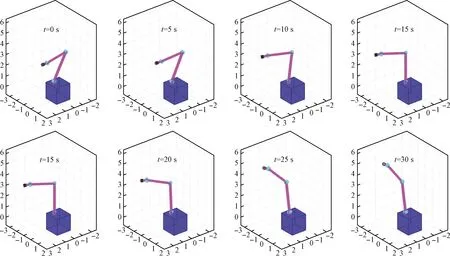
图6 空间机器人运动过程Fig.6 Space robot motion processes

其中，机械臂中间构型和终端构型分别：

(33)

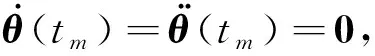
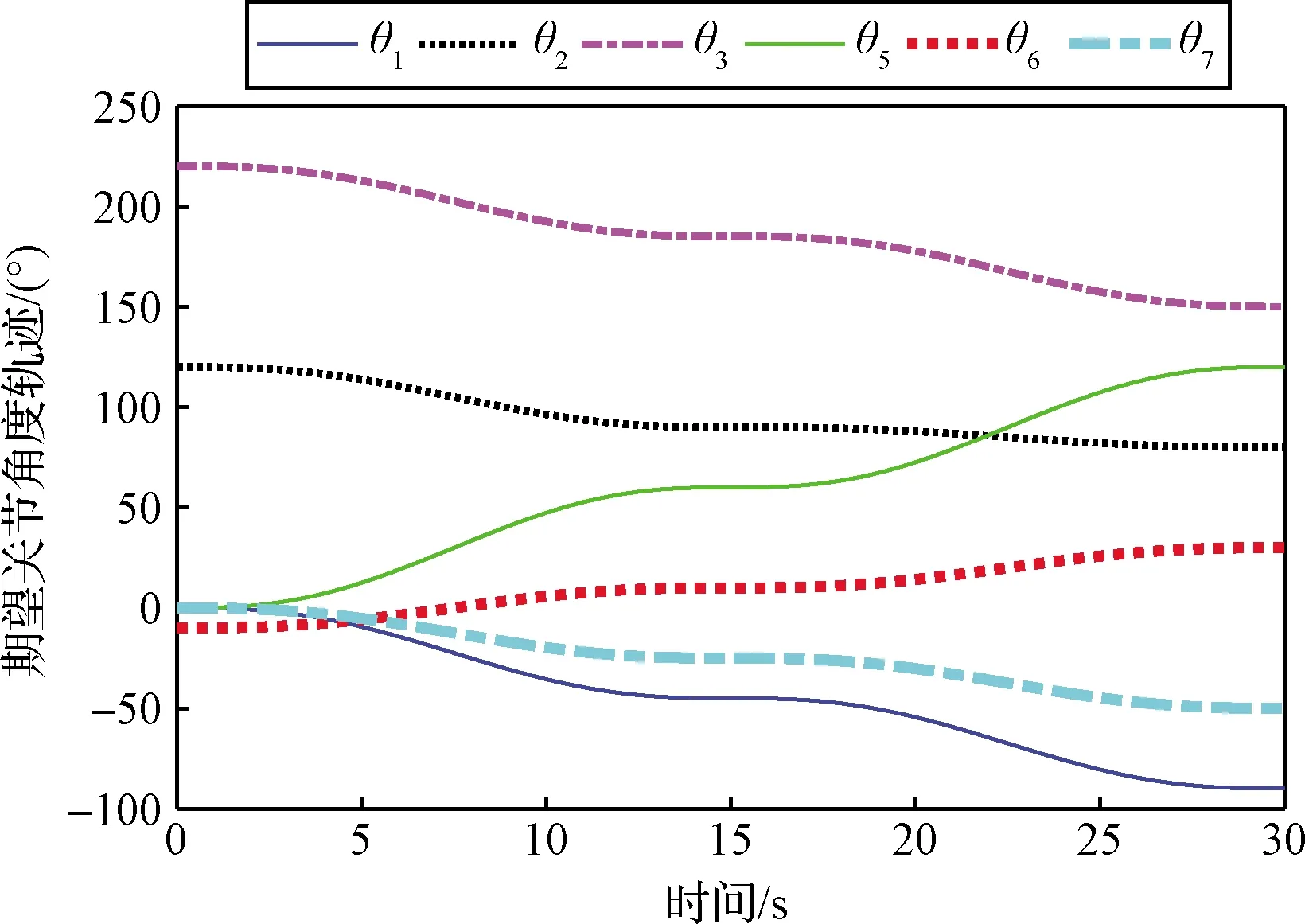
图7 机械臂期望关节轨迹Fig.7 Desired joint trajectories of the manipulator

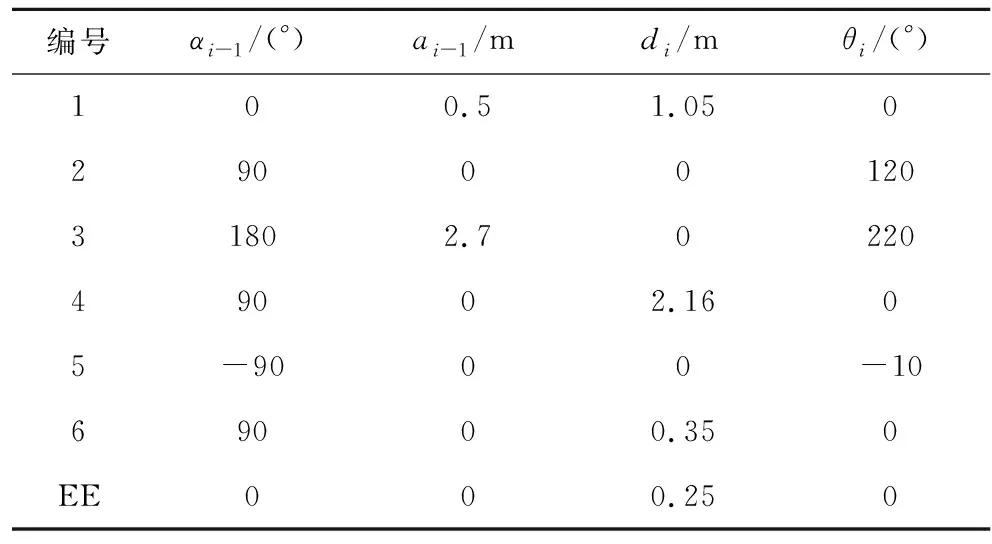
表2 空间机器人系统的D-H参数Table 2 D-H parameters of the space robot system

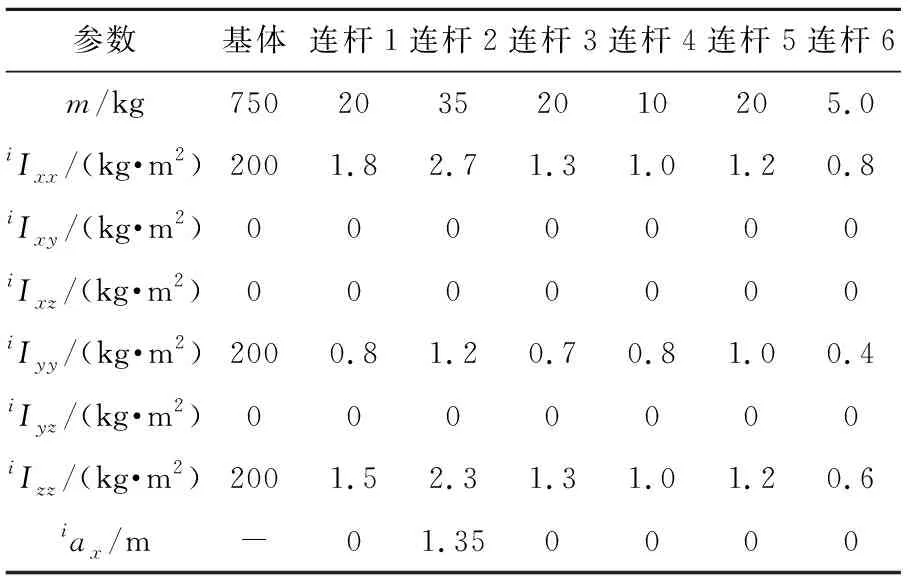
表3 空间机器人系统惯性参数Table 3 Inertial parameters of the space robot system

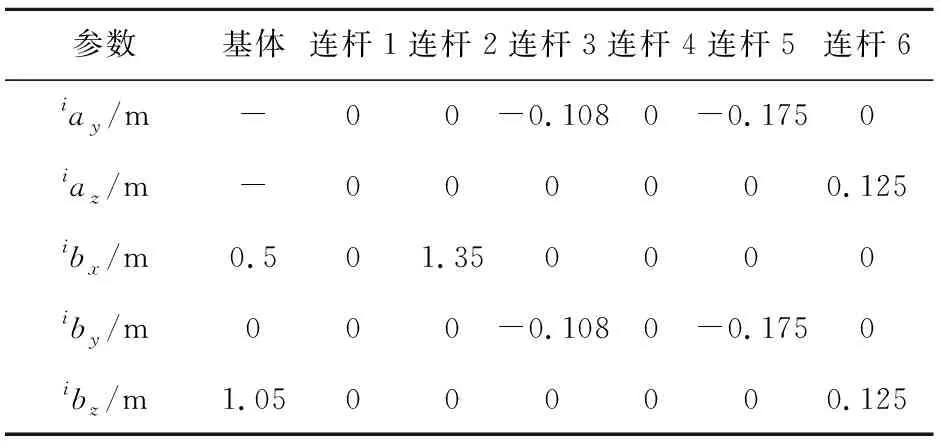
续表3

4.1 案例1：名义模型

本案例采用理想的名义模型，即式(14)，来验证CTC和TDE控制器。CTC控制器参数设定为：

KP[0, 0, 0, 75, 50, 50, 50, 50,

50, 5, 5, 0.8]T×105，

KD[0, 0, 0, 500, 500, 500, 500, 500,

500, 20, 80, 1]T×102。

对于TDE控制器，系统周期采样间隔设为：δ=0.5 ms，相关参数设定为：

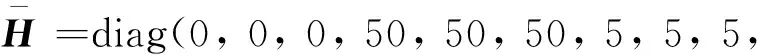
0.5, 0.5, 0.5),

KP[0, 0, 0, 10, 10, 10, 2, 2, 2,

1, 1, 1]T×102,

KD[0, 0, 0, 20, 20, 20, 4, 4, 4,

2, 2, 2]T×101。

由于控制器不控制基体位置，故上述参数前3个元素均设为0。本案例仿真结果如图8所示。

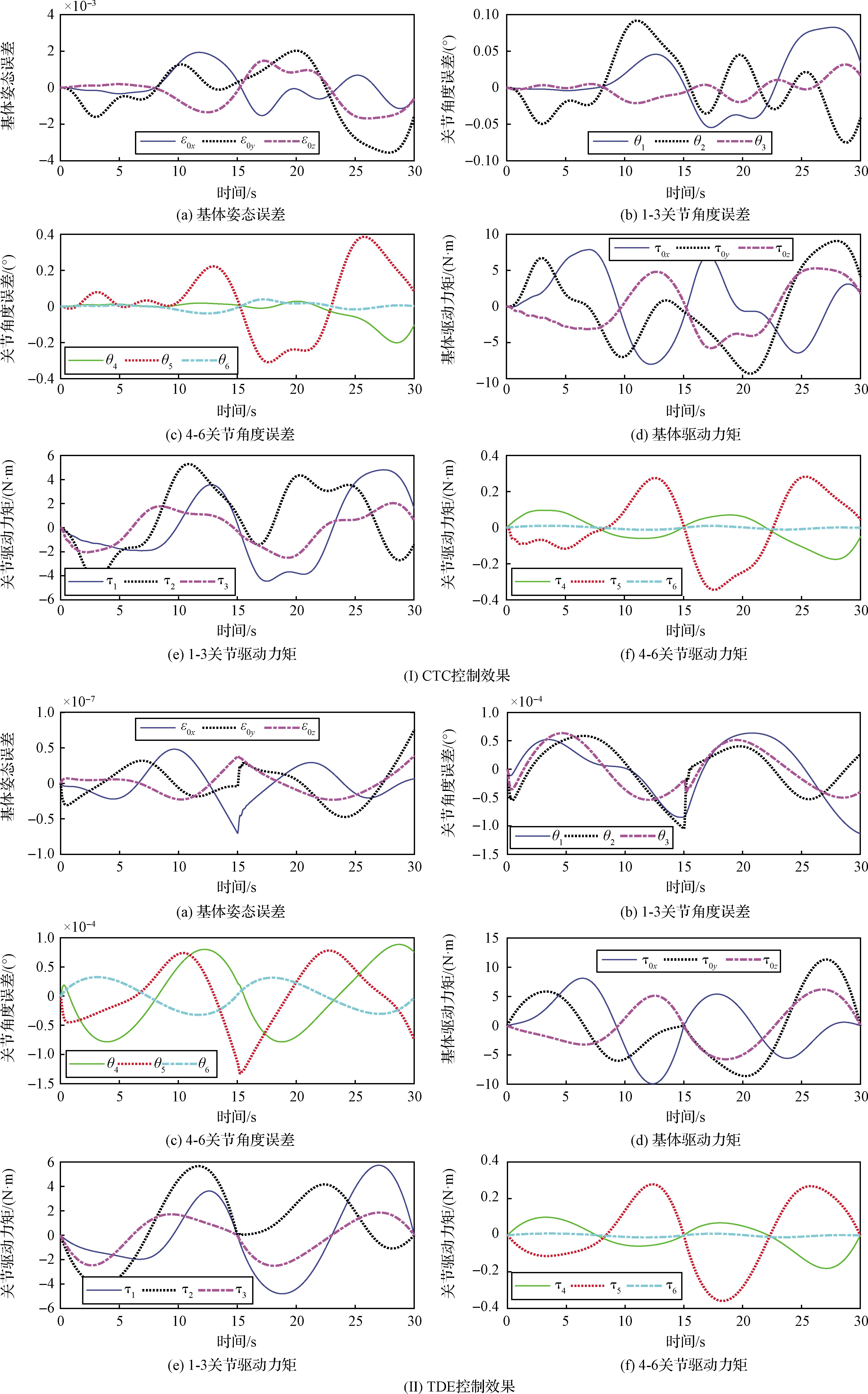
图8 案例1仿真结果Fig.8 Simulation results of the case 1

4.2 案例2：考虑扰动

本案例在名义模型的基础上，考虑外界扰动，设未知扰动力矩为：

(34)

这里，CTC和TDE控制器参数与案例1中控制器参数一致，仿真结果如图9所示。

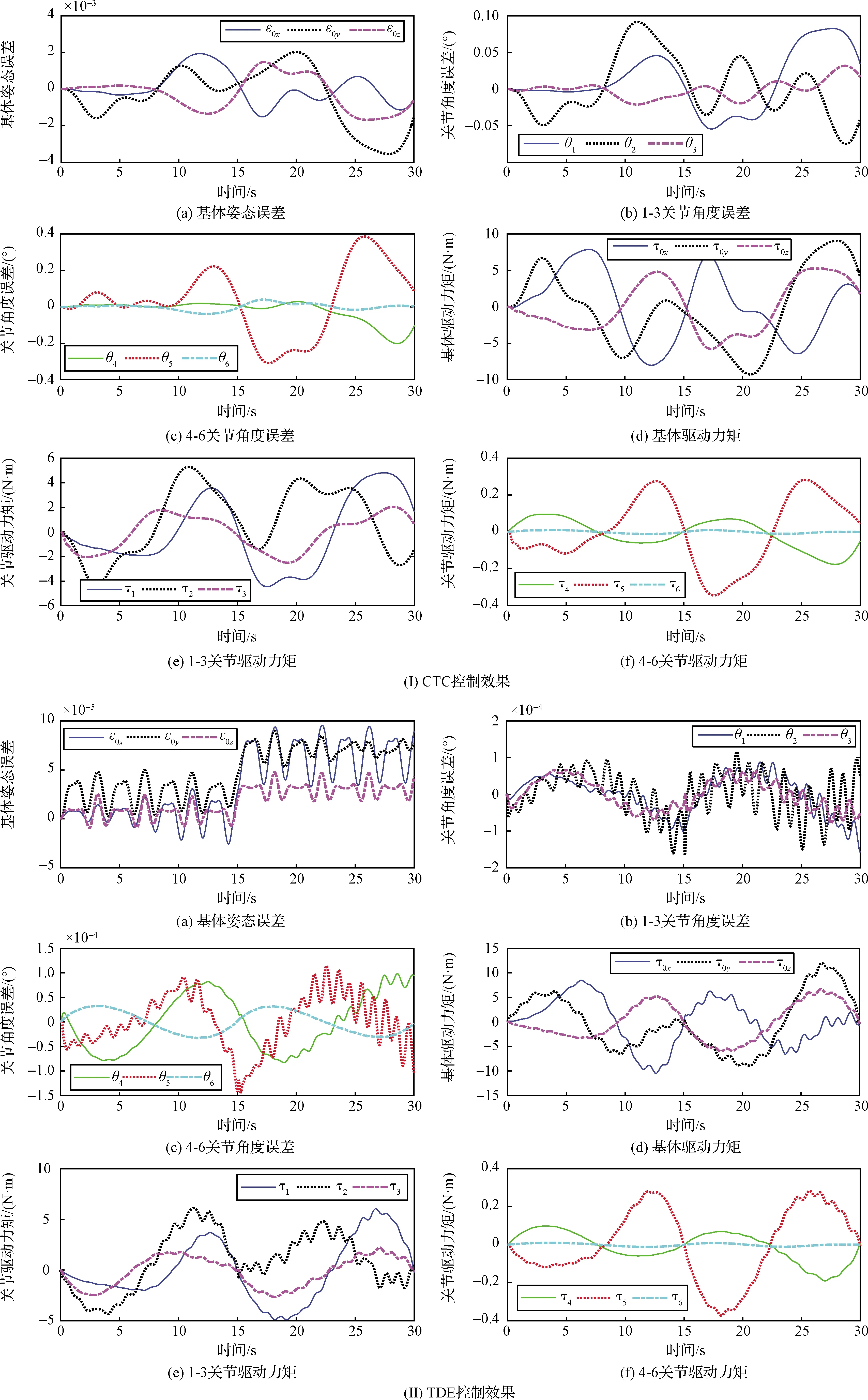
图9 案例2仿真结果Fig.9 Simulation results of the case 2

4.3 案例3：考虑扰动和不确定性

本案例同时考虑扰动和不确定性因素，假设系统不确定性由末端未知载荷引起，导致末端连杆参数发生变化。设末端惯性质量和惯性矩变为：m6=20 kg,6I6xx=6I6yy=1.2 kg·m2,6I6zz=1.0 kg·m2。尽管，参数发生变化，但对于控制器是未知的。这里CTC和TDE控制器参数同样与案例1中控制器参数一致，仿真结果如图10所示。

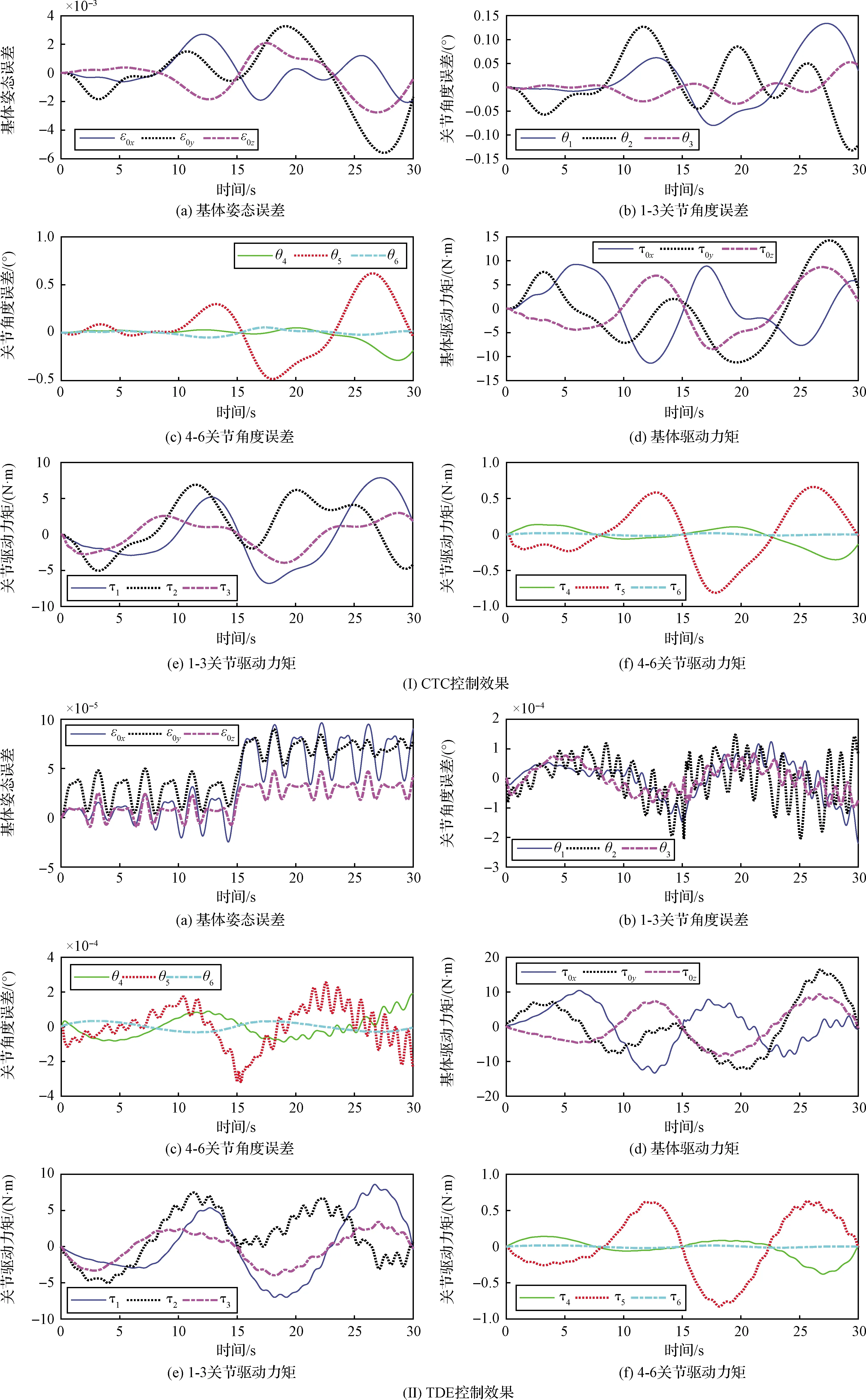
图10 案例3仿真结果Fig.10 Simulation results of the case 3

4.4 分析与讨论

由于四元数仅具有3个独立变量，故在仿真案例中用四元数的标量部分来表示基体姿态。从图8～10中，在3个案例中，对于CTC方法，基体姿态误差约在10-3量级；而对于TDE方法，基体姿态误差最大值约在10-5量级；因此TDE解耦控制在维持基体姿态稳定方面效果更优。另一方面，在机械臂关节轨迹控制精准性方面，对于CTC方法，机械臂关节的最大跟踪误差约在10-1量级；对于TDE方法，机械臂关节最大跟踪误差约在10-4量级；因此TDE解耦控制在保证机械臂运动精准性方面效果更优。根据TDE原理可知，TDE控制具有内在的自适应性，因此在外界高频扰动的作用下，TDE能够精准地估计扰动力的大小和变化，具体体现在TDE的控制驱动力矩方面。综合TDE的解耦机理，可以看出基于TDE的无模型解耦控制方法，不仅效率更高，且解耦效果更好。