基于动态特性描述的变量加权型分散式故障检测方法

钟 凯 韩 敏 韩 冰

1.大连理工大学电子信息与电气工程学部 大连 116023 2.上海船舶运输科学研究所航运技术与安全国家重点实验室 上海200135

随着现代工业水平的迅猛提高,其生产规模和生产过程的复杂性也大大增加,为了保障工业安全和产品质量,过程监控和故障诊断技术也显得愈发重要[1-2].传统的基于模型的过程监测方法依赖于精确的数学模型或充分的先验知识,极大地限制了其在实际中的应用.而基于数据驱动的方法无需建立精确的过程机理模型,直接对过程运行数据进行分析和处理,据此建立描述过程运行状态的统计模型,因此很适合于监测难以建模的复杂工业过程,主要包括,适合于故障分类和诊断的费舍尔判别(Fisher discriminant analysis,FDA)[3],主成分分析(Principal component analysis,PCA)[4],利用质量变量引导过程变量样本空间分解的偏最小二乘(Partial least squares,PLS)[5]以及适用于非高斯过程监测的独立主元分析(Independent component analysis,ICA)[6].特别地,PCA 作为一种最主要的数据驱动方法,能够有效地进行数据降维和潜在特征的提取,并且在上述方法中具有最低的计算复杂度,因此受到工业界和学术界的广泛关注,并在故障检测和诊断领域取得了丰富的研究成果[7-8].

实际工业过程采集的过程数据一般都在时间上序列相关,而基于传统的PCA 方法的过程监控并没有考虑数据间的此种关联,以至于主成分甚至残差都具有未被建模的动态特性,因此并不适用于动态过程的建模.文献[9]首先使用延时测量值扩充分析数据阵,然后对该增广数据阵实施PCA 分解以建立数据间的动态关联,进而提出了动态PCA(Dynamic PCA,DPCA)的主体框架.此后,DPCA在理论和应用上仍有后继的发展[10-11].最近,文献[12]利用自回归模型提取数据间动态潜隐成分(dynamic latent variables,DLV),而PCA 模型用于建立残差的静态关系,因此静态关系和动态关系都得到了很好的表征,从而提高了动态过程的故障检测效果.

然而,以上所涉及的方法都是单个集中的模型,不适用于目前大规模的工业过程故障检测,而分散式建模策略由于其具有较低的计算复杂度,较好的模型灵活性和较强的容错能力等优点,已成为监控大规模工业过程的有力手段[13-14].更进一步,文献[15]利用动态特性选择准则并结合分布式建模的优势,成功地解决了大规模动态的故障检测问题.但其在选择子模型变量时所依赖的动态特性准则是一种单纯的线性关系指标,无法评估变量之间的非线性关联,因此并没有取得最优的故障检测效果.文献[16]又提出一种基于互信息(Mutual information,MI)的分散式动态PCA 故障检测方法(MI-DPCA),MI 准则同时考虑了变量间的线性和非线性关系,较好地处理了数据的动态性问题.然而在分散式子块中基于MI 准则选择的变量之间往往存在较大的冗余,从而导致欠佳的故障检测结果.文献[17]提出了一种基于最大相关最小冗余(Minimal redundancy maximal relevance,mRMR)变量选择的PCA 故障检测,解决了由MI 准则带来的变量间冗余问题,取得了较好的故障检测效果.但该模型采取简单地剃除mRMR值超过设定阈值的变量来实现变量选择以建立相应的子块,因此直接忽略了对当前变量影响较小的测量变量,并且也不能定量描述保留下的不同测量变量对当前变量的影响程度,此外该模型也无法解决动态过程的监控问题.

基于以上分散式建模的优势以及描述变量间动态关系方法的不足的讨论,并受到文献[18]的启发,本文提出了一种基于动态特性描述的变量加权型分散式故障检测方法(Minimal redundancy maximal relevance—weighted dynamic principal component analysis mRMR-WDPCA).全文主要创新点如下:

1)与传统的变量选择方法[15-16]相比,mRMR算法考虑了动态过程中变量间的线性和非线性关联的同时也显著地减少变量间存在的冗余,从而能更准确地描述变量间的相关性关系.

2)根据变量间mRMR 值的大小对动态增广矩阵中所有测量值赋予不同的权值,避免遗失含有有用信息的变量,且不同延迟变量对当前测量值的影响大小就通过权值来体现,因此能更加全面地刻画该测量值的动态特性.

3)提出一种融合mRMR 算法,贝叶斯推理以及DPCA 模型的加权型分布式建模策略,提高了模型的容错能力和泛化能力,取得了更好的故障检测结果.为全流程动态过程监控方案的设计提供了新的思路.

1 基本方法理论

1.1 PCA 和DPCA 模型

1.2 MI 和mRMR

2 mRMR-WDPCA 的故障监测方法

2.1 基于mRMR 动态特性描述

图1 基于mRMR 的动态特性描述Fig.1 mRMR-based dynamic feature characterization

由上述描述可知,与常规的DPCA 对所有的(d+1)m个变量赋相同的权值,亦或是与其他直接剔除某些相关性较弱的变量选择方法相比,式(9)加权了所有的变量,在避免信息损失的同时,还通过较大的权值强调了相关程度较大的变量带来的“积极作用”,而相对小的权值也抑制相关程度较小的延迟变量所带来的“次要影响”,更能体现变量的动 态特性.

2.2 mRMR-WDPCA 方法离线建模和在线监测

在上一节的动态特性描述方法的基础上,我们给出如图2所示的包含离线和在线两部分的监控流程,具体细节介绍如下.

图2 基于mRMR-WDPCA 故障监测的流程图Fig.2 Flowchart of mRMR-WDPCA based fault detection

2.2.1 离线建模

步骤1.通过对X中每个测量变量引入其前d个采样值,以获取如式(2)中的增广矩阵.

步骤2.对增广矩阵的每一个测量变量实施第2.1 节的动态特性描述准则,以获取Xa中每一列的权值向量,并按式(9)求取Xi.

步骤3.对Xi建立基于PCA 的监测模型,并重复 此步骤以获得m个PCA 监测模型.

2.2.2 在线监测

3 仿真算例

TE(Tennessee-Eastman)工业过程由文献[23]首次提出并已经成为验证过程控制和故障诊断方法的标准实验平台,其流程如图3所示,主要包含5 个主要单元:反应器、冷凝器、分离塔、汽提塔和压缩机.主要涉及8 种反应成分:A、B、C、D、E、F、G 和H.整个过程中共有12 个操作变量和41 个测量变量,还有21 种不同的预设故障,每个故障都有相应的训练样本和测试样本[24],相应地,故障都从第160 个采样点开始引入,且本文涉及的所有仿真数据都可从网站http://web.mit.edu/braatzgroup/links.html 上下载.本文依据文献[25]选择了过程中的11 个操作变量和22 个测量变量共33 个变量作为监测对象,且假设所有数据都服从高斯分布.

图3 TE 过程的结构图Fig.3 Structure diagram of the TE process

离线建模阶段,将正常工况下的960 数据作为训练集建立DPCA、DLV 以及MI-DPCA 的监控模型,以作为本文方法的对比,为了更好地进行比较,所有方法的置信水平α都设置为99%.DLV 监测模型采用了3 个统计量,分别为和Qr,分别用于监测动态潜隐成分、静态潜隐成分和残差,关于该模型的具体介绍可参考文献[12],此处不再赘述.而对于DPCA 和MI-DPCA 模型中的延迟测量值d可根据文献[7]中提供的方法确定为2,保留的主元个数可通过累计方差贡献率准则(CPV ≥85%)确定为34.且本文提出的mRMR-WDPCA方法中的延迟测量值d=2 ,而每个子PCA 模型中的主元个数同样由CPV ≥85% 准则确定为1.

首先利用TE 过程中500 组正常数据作为测试样本集测试DPCA、DLV、MI-DPCA 以及本文的mRMR-WDPCA 模型对正常工况的误报率(第I型错误),具体的实验结果如表1所示,由表1 可知,虽然所提方法两个统计指标都没有取得最低的误报率,但是从工程实践角度来说,监控过程中连续6个采样点超过控制线时才被认为有故障发生,而由于mRMR-WDPCA 两个指标分别对应的误报率1.63%和 2.13% 都是通过单一采样点计算求得的,所以所得结果仍然处于可接受的范围内,所提方法在监控正常工况时也是有效的.

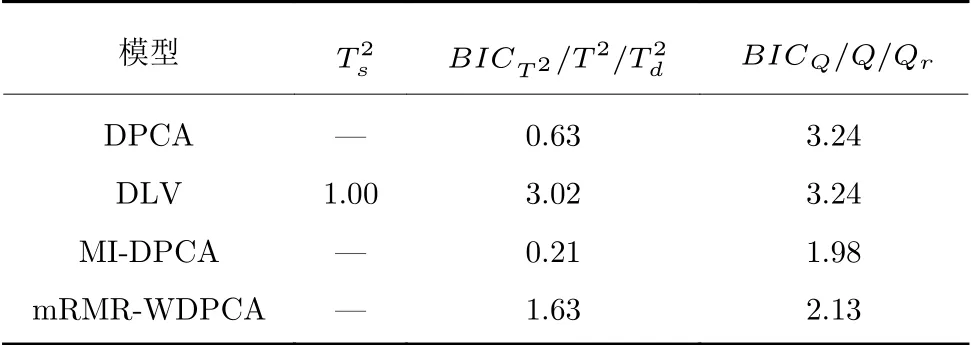
表1 TE 过程的误报率(%)Table 1 False alarm rates of TE process(%)

通常来讲,较低的故障误报率会对应着较高的故障漏报率,为了进一步说明所提方法的优越性,还需对比4 种方法的故障漏报率(第II 型错误).即分别利用4 种方法来检测TE 过程的21 种故障,并记录每种方法不同统计量中较好的检测结果,详见表2.其中,由于故障3,9 和15 发生时不会引起样本数据均值或方差的显著变化[26],因此很难被本文中以数据均值和方差为诊断特征的mRMR-WDPCA 方法有效地检测出来,所以,上述3 种故障在本研究中不予考虑.但已有一些基于流形学习[27]或子空间分解[28]的数据驱动方法仍可以成功检测、诊断以上3 种故障.剩余的18 种故障对应的最小的漏报率以及检测延迟数在表2 中都标记为粗体,以方便辨识.

从表2 中可以看出,所提方法在大多数故障类型上都能取得优越于其他三种方法的漏报率和检测延迟数.特别地,对于故障10 和16 的漏报率得到大幅的降低.主要是因为mRMR-WDPCA 模型考虑变量间的线性和非线性关联同时减少变量间存在的冗余,还通过不同权值的赋予,“凸显”了重要延迟变量作用的同时也“弱化”了次要延迟变量的次要影响,因此所建立的监控模型能更加全面地描述当前测量变量的动态特性,从而能进一步提高故障的监测效果.即便是mRMR-WDPCA 方法没有取得最好结果的故障,但所得结果与最优的漏报率也相差无几.此外,4 种方法对剩余的18 种故障的平均漏报率结果如图4所示,其中,DLVT表示DLV方法的两个统计量和的均值,从图4 中可知,相比于其他三种方法,本文所提模型的不同统计量都取得了最低的平均漏报率,因此从另一个角度说明了方法的有效性和实用性.

图4 4 种方法的故障平均漏报率Fig.4 Average missing alarm rates of the four methods

表2 TE 过程故障漏报率(%)和检测延迟数(个)Table 2 Missing alarm rates(%)and detection delay(delayed samples)of TE process

为了更好地展示mRMR-DDPCA 方法相比于其他对比方法的有效性,特将4 种方法对故障10和16 这两种不同类型的故障的监控细节列于图5和图6 中.具体地,从图5(d)中可以看出,mRMRDDPCA 方法的 BICQ统计量不但取得了最低的漏报率18.88%,而且在第163 个采样点就检测出了故障,故障延迟数为2,而其他三种方法对应的延迟数分别为18,7 和24,说明本文方法能在故障发生后

图5 故障10 的过程监控结果Fig.5 The monitoring charts of Fault 10

最快地将其检测出来.此外,当故障被检测到之后,mRMR-DDPCA 模型对应的统计量曲线很少回落到阈值线以下,而3 种对比算法的统计量曲线都会出现不同程度的回落现象,从而导致较高的漏报率,进而说明了所提方法故障检测的稳定性和持续性.类似地,图6 中对于故障16 的监测细节同样说明了所提方法的优越性.

图6 故障16 的过程监控结果Fig.6 The monitoring charts of Fault 16

4 结论

针对大型工业系统常常伴有复杂的动态特性,且变量间的相互影响会体现在不同的采样时刻上等问题.本文利用分布式mRMR-WDPCA 方法充分刻画变量间相关性的同时,也通过不同权值的赋予定量地描述了不同延迟变量对当前测量变量的影响程度,凸显了变量间的相关性差异,从而更好地解决了测量变量的动态特性问题,取得较好的故障检测结果.在TE 过程上的仿真实验验证mRMRWDPCA 相对于其他方法的优越性.然而,本文仅局限于故障检测的分析,而后续的故障诊断问题还未有所涉及.此外,所提的mRMR-WDPCA 方法仍是一种线性模型且假设训练数据服从高斯分布,如何将方法拓展以处理非线性、非高斯复杂过程仍是值得进一步研究之处.