基于图谱域移位的带限图信号重构算法

2021-11-13郭文彬

自动化学报 2021年9期

杨杰赵磊郭文彬,2

1.北京邮电大学北京 100786 2.通信网信息传输与分发技术重点实验室石家庄 050000

随着信息技术的高速发展,各领域中所产生的数据维度正在以前所未有的速度增长,例如社交网络数据、金融交易数据和城市交通流量数据等.

然而,传统的数据表征方法无法适用于具有复杂关联特征的网络数据集.所以,图网络[1]——一种非规则域中用于表征关联数据的模型应运而生.如何更好地分析这些基于图网络表征的数据集,从而更加高效地挖掘数据集的深度信息成为当下研究的热点问题之一.

近年来,随着图信号处理的兴起和发展,图网络中的信号(数据)分析与处理引起了研究者们的广泛关注.图信号处理是将传统的信号处理理论衍生至基于图网络表征的非规则域信号处理理论[2].目前,图信号处理的理论研究主要包括图滤波器(组)的设计[3]、图信号采样/恢复[4]、图信号压缩[5]和图拓扑学习[6]等.相关的应用研究有传感网络中的异常数据检测[7]及修复[8],基于图数据的机器学习等[9-10].然而,目前该研究领域中仍然存在着许多亟待探索和解决的理论问题和应用瓶颈[11].例如,图信号处理中尚未出现类似于奈奎斯特采样定理的统一采样理论[12].相关的挑战还包括图信号的大规模分布式计算[13]、异构网络中的图信号处理[14]、如何融合多尺度下的图信号特征而进行信号多分辨分析[15],以及如何分析张量图网络中的多层图数据之间的关联性[16]等.随着图信号处理的不断发展,必将成为有效应对数据泛滥现象和降低数据冗余的重要工具,并为网络数据的高效处理提供理论支撑.

由于存在图网络的拓扑结构复杂多变以及数据维度带来的计算消耗大的问题,如何利用尽可能少的采样节点信号和网络拓扑信息更加高效和完备地表征未采样节点信号,从而为网络数据的传输和处理提供高效的技术支撑是图信号处理中的核心问题[17].在图信号重构的相关研究中,由于带限图信号重构问题可作为其他类型图信号重构问题的源问题进行相关推广;如何设计高效的带限图信号重构算法是一个重要的研究课题,它为设计平滑图信号重构算法和实际网络数据重构方法提供了理论基础.

基于Papoulis-Gerchberg 信号重构算法[18],Narang 等[19]提出一种基于空域迭代图滤波的信号重构方法(Iteration least square reconstruction,ILSR).该方法通过将采样信号和每次迭代后产生的采样信号残差进行累加后,再进行图谱域带限滤波处理,从而达到重构目的.在ILSR 重构算法的基础上,Wang 等[20]提出了基于迭代加权策略的信号重构算法(Iteration weighting reconstruction,IWR)和基于迭代传播策略的信号重构算法(Iteration propagating reconstruction,IPR),两种算法优于ILSR 算法的原因在于对采样节点进行了残差滤波处理.在IWR 算法中,Wang 等[20]首先将采样信号的残差扩大相应的权重,然后进行图滤波处理;而在IPR 算法中,首先是基于预先划分好的局部集将采样节点的信号残差传递给相邻的未采样节点,然后进行图滤波处理.由于两种算法在每步迭代中加入了对于采样信号残差的处理,增大了未采样信号在插值过程中的增量,进而提高了重构的效率和精度.为了进一步地提高对于残差信号的估计精度,Yang 等[21]提出了基于扩散算子的迭代重构算法(Iteration graph reconstruction based diffusion operator,IGDR).IGDR 算法修正了IWR 和IPR算法中由于采样信号残差在局部集内均匀传递而导致的过平滑现象,在每步迭代中基于局部扩散算子和全局扩散算子对信号采样进行了联合处理,使得迭代滤波得到的未采样信号为图带限滤波信号和残差扩散信号的总和.不同于IWR、IPR 和IGDR 算法聚焦于迭代残差信号的处理方法,Brugnoli 等[22]同样在ILSR 算法的基础上提出了基于最优参数的Papoulis-Gerchberg 信号迭代重构算法(Optimal Papoulis-Gerchberg iterative reconstruction,OPGIR),该算法通过在每步迭代中设置松弛参数的最优解而达到较高的迭代效率.

不同于基于空域滤波的重构算法研究,为了完善图信号谱域理论框架及提升图信号的谱域特征分析能力,基于图傅里叶变换的图谱域重构算法同样是近年来的研究热点.

Tseng 等先后提出基于压缩感知的硬阈值截断图谱域重构算法[23]和基于图傅里叶变换的图谱域重构算法[24].在硬阈值截断图谱域重构算法中,作者首先将图信号重构问题转化为图谱域中的稀疏优化问题,然后采用经典压缩感知理论中的基追踪算法和正交匹配算法或迭代硬阈值截断法分别进行求解.通过上述方法估计出未采样图信号在图谱域中的频率分量,最后基于图傅里叶逆变换将估计的频率分量转换为空域图信号.在正交匹配算法的基础上作者又提出了基于图傅里叶变换的信号重构算法;在正交匹配算法中,完整频率分量是通过逐步重构出每个图频率分量值而实现的.而在基于图傅里叶变换的信号重构算法中,作者通过重构出小于截止图频率内的频率分量值实现信号重构.该算法实质上是将ILSR 算法转化到图频域进行处理.然而,两种方法并没有针对低通带限图信号的谱域特性进行更深入的分析,只是将空域重构算法转化到变换域进行.

本文首先基于图傅里叶变换的分块矩阵形式和图带限信号特性分析得出图带限分量的恒等不变性.基于该特性,本文将重构问题建模为一个最小二乘模型.本文所提出的重构模型是根据图高频部分的恒等关系,相比于基于图低频段相似性的ILSR重构模型,更加能够准确地表征信号的图谱域带限特性,提高了重构精度.此外,由于根据重构模型而设计的迭代算法采用拟牛顿法进行求解,在避免海森矩阵求解的同时高效利用了模型的二阶梯度信息,相比于ILSR 和O-PGIR 提高了迭代效率.而在基于残差信号的重构算法中,本文根据残差信号同样具备图带限分量的恒等不变性,设计了一种基于残差谱移位的重构算法.相比于IWR/IPR 和IGDR 算法,本文算法具有较好的重构性能.此外,由于本文提出的图带限分量的恒等不变性不需要考虑带限频率所在的频段,所以针对分段带限图信号的重构问题同样适用,并且具有良好的重构性能.

1 基于谱移位的重构算法

图1 带限图信号Fig.1 Graph band-limited signals

2 基于残差谱移位的重构算法

3 分段带限图信号重构算法

4 实验仿真及分析

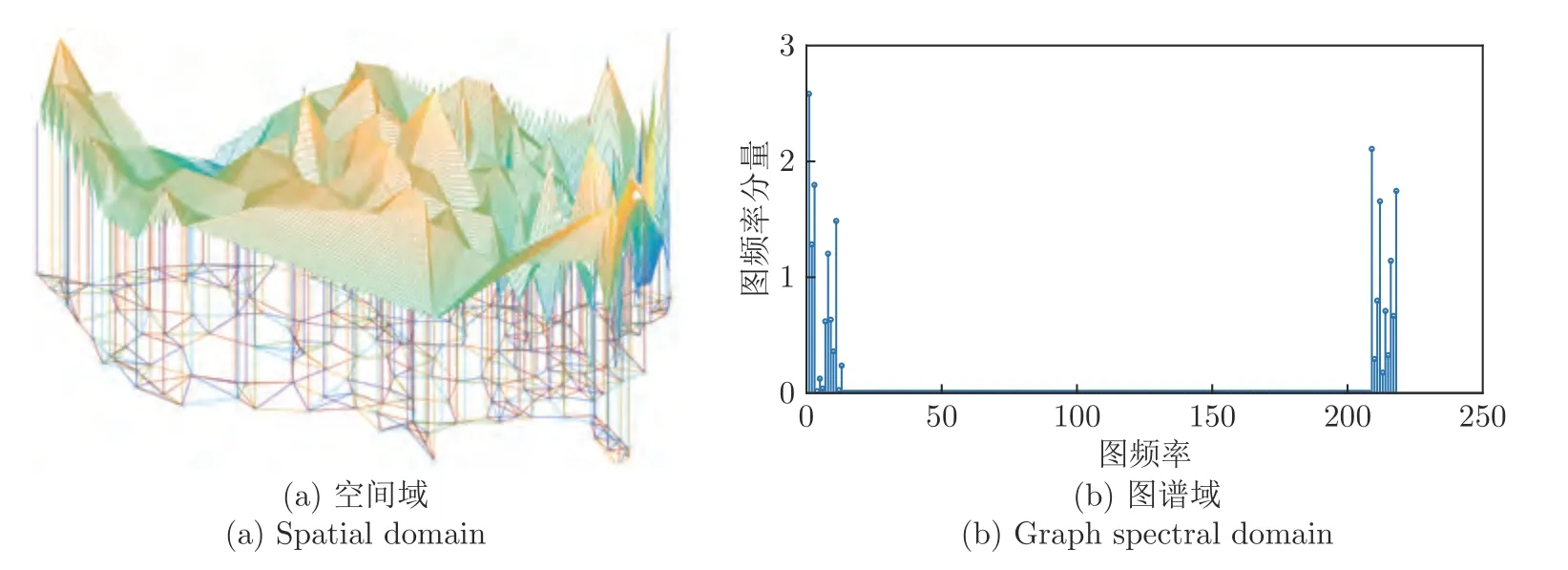
图2 分段带限图信号Fig.2 Graph sperate band-limited signals

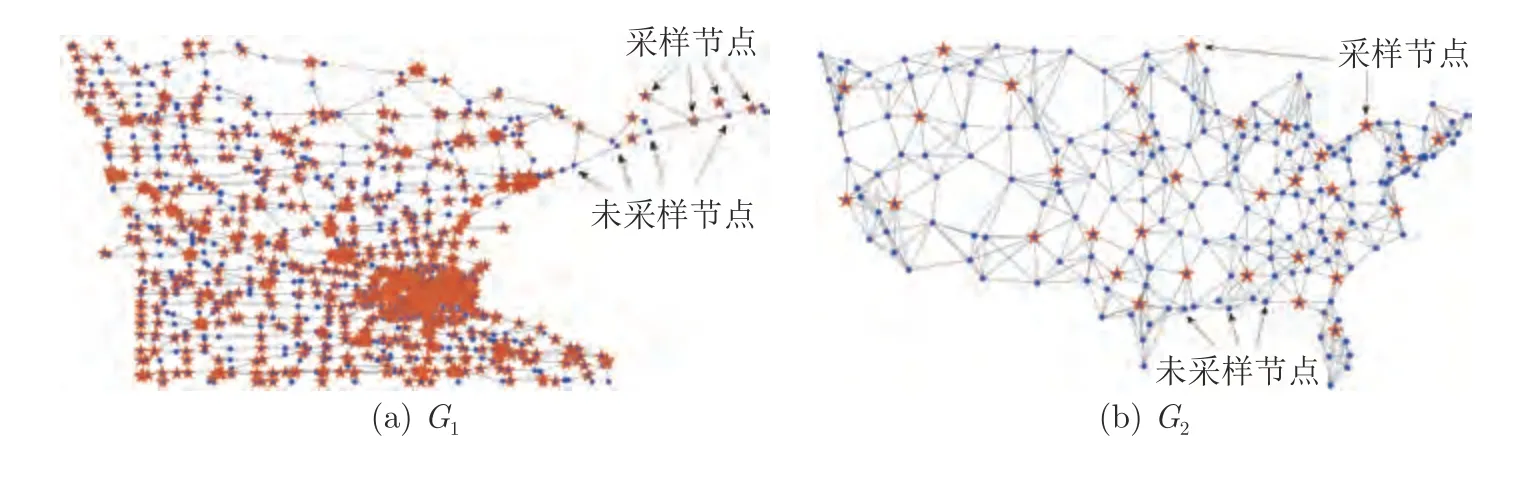
图3 图信号采样Fig.3 Graph signals sampling

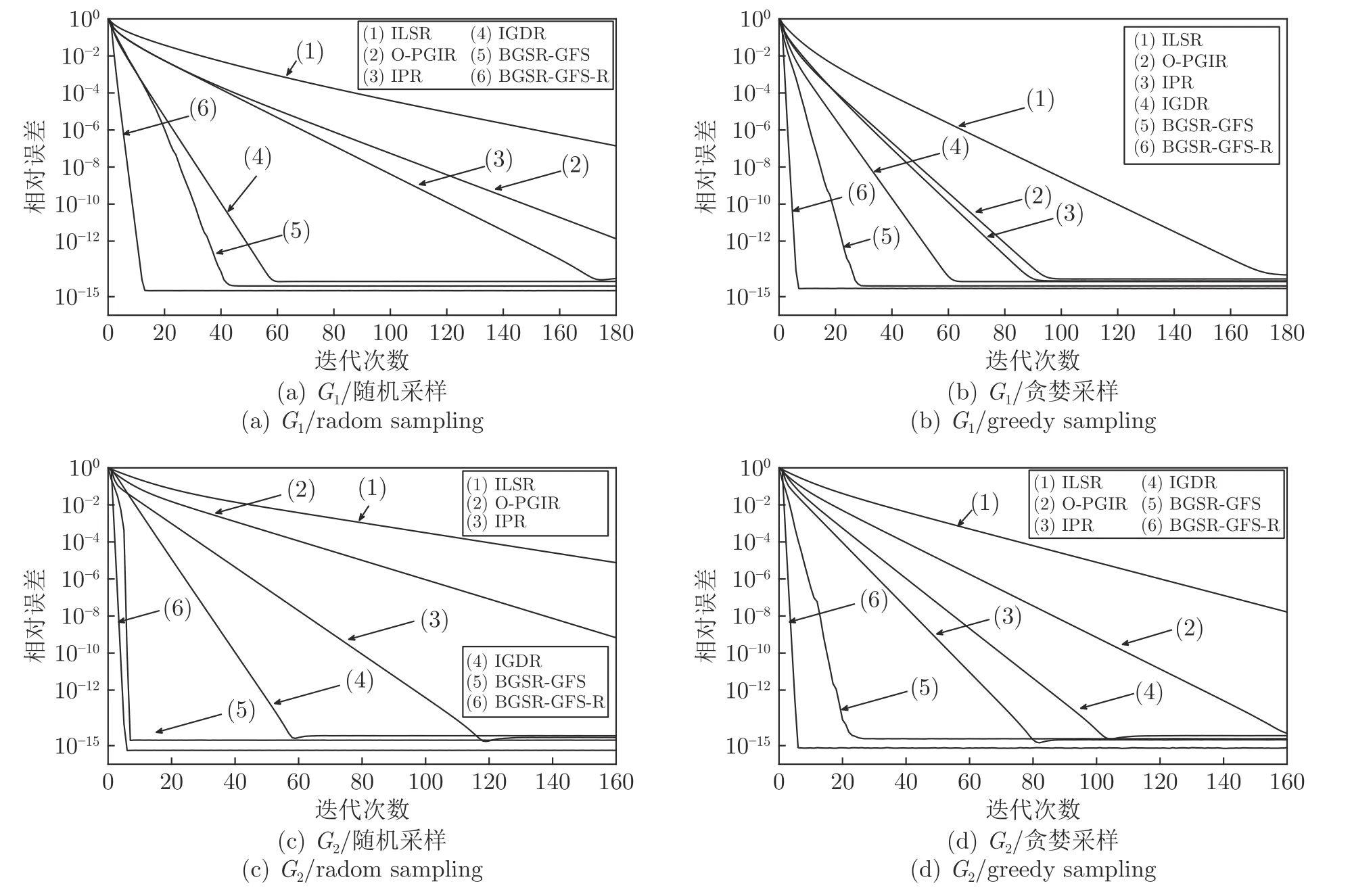
图4 无噪环境下带限图信号重构性能对比Fig.4 Comparison of graph band-limited signals reconstruction performances in noiseless environment

表1 无噪情况下基于随机采样的 G1 重构效率Table 1 G1 reconstruction efficiency of random sampling in noiseless

为了对比噪声环境中的算法的鲁棒性,本文在采样信号中分别加入信噪比为 20 dB 和 40 dB 的随机高斯噪声.信号重构性能对比如图5所示,本文提出的重构算法和对比算法的抗噪鲁棒性相同,然而BGSR-GFS 和BGSR-GFS-R 的迭代效率更高.无论是本文算法还是对比算法均没有进行噪声抑制或消除的步骤,导致无法消除噪声对于重构性能的影响.

图5 含噪环境下带限图信号重构性能对比Fig.5 Comparison of graph band-limited signals reconstruction performances in noisy environment

表2 无噪情况下基于随机采样的 G2 重构效率Table 2 G2 reconstruction efficiency of random sampling in noiseless

在第3 组仿真中,本文将针对分段带限图信号进行重构性能对比.本文将第1 组仿真实验中的图信号加入高频分量.即随机选取Q个连续的高频分量后,再通过图傅里叶逆变换得到分段带限图信号(G1和G2的Q值分别为10 和3).为了确保对比试验的公平性,本文将对比算法中的低通图滤波器调整为带通图滤波器.

如图6所示,无论是基于随机采样或贪婪采样,本文算法都具有良好的重构精度和迭代效率.由于ILSR 和O-PGIR 算法都是利用图信号的低频分量相似性原则设计重构算法,而没有考虑到图信号的高频段分量的差异性,所以迭代效率十分有限.算法IPR 在ILSR 的基础上,基于相邻节点残差信号等值传递的原则进行迭代过程中增量的估计,而算法IGDR 在IPR 的基础上增加了扩散策略,进一步提高了迭代效率;两种基于残差法的重构策略实质上都是利用了残差信号低频分量之间的相似性,同样无法实现高效的信号重构.与上述4 种算法不同的是,由于本文提出的两种算法同时考虑了图低频相似性和图高频差异性,通过图谱域移位策略重构分段带限图信号,具有较高的重构精度和迭代效率.