一种四自由度并联机器人的运动性能分析及仿真

胡琼琼，伞红军，陈久朋，谢飞亚，陈中平，李鹏宇

(1.昆明理工大学 机电工程学院,云南 昆明 650500;2.中国人民解放军 第78098部队,四川 成都 610200)

并联机器人是机器人学的一个重要分支。并联机器人承载能力强，输入误差不积累，动力性能好，且运动控制简单。自1965年Stewart机构诞生以来，并联机构迅速成为国际机器人学领域的研究热点之一[1-3]。在实际生产中，并联机器人与串联机器人因具有各自的优缺点，扩大了机器人应用领域。目前，结合串联和并联机器人优势的混联机器人的诞生虽然在一定程度上解决了机器人工作空间问题，但是其运动控制还是基于并联机器人原型。

相对于6自由度并联机构，少自由度并联机构结构简单、生产成本低、易于操作，拥有更广阔的发展前景与发展潜力[4]。国内对并联机器人的研究起步较晚，特别是针对机构综合与分析等方面的研究较少。在少自由度并联机构的综合和运动性能研究方面，文献[5～7]提出了基于方位特征的并联机构拓扑结构设计理论与方法；文献[8～9]提出了基于约束螺旋理论的机构自由度分析的原理和方法。这两种分析方法均在并联机构的综合上做出了一定的贡献。文献[10]基于方位特征理论提出了一类3T1R型四自由度高速并联机械手。文献[11]基于螺旋理论提出了一种4-URU型并联机器人构型。文献[12]对2-TPR/2-TPS并联机构进行了仿真分析，验证了该机器人运动自由度的正确性。

本文基于方位特征理论与方法，对3-TRT/SPS并联机构进行结构拓扑分析，求解了其独立自由度。随后，在机构分析的基础上采用解析法获得了机器人正反解，并使用极坐标搜索法求出了机器人工作空间，为少自由度并联机器人的发展做出了一定贡献。

1 机器人的结构特点

3-TRT/SPS的三维模型如图1所示。该并联机器人具有4个支链、3个对称分布的TRT支链以及连接动、定平台的SPS支链。每个TRT支链由连接动、定平台的两个虎克铰T(由两个相互正交的转动副组成)和一个转动副R组成。每个TRT支链可以看作是由5个转动副组成，其中和上下平台相连的两个转动副轴线互相平行，其余3个转动副轴线互相平行，且与另两个转动副轴线垂直。SPS支链由两个球铰和一个移动副组成，两个球铰分别与动静平台的几何中心相连。为了方便描述机器人的运动，可建立如图2所示的拓扑结构简图。该简图清楚地描绘了整机的连杆和运动副配置。

图1 3-TRT/SPS并联机器人三维模型Figure 1. 3D model of 3-TRT/SPS parallel robot

图2 3-TRT/SPS并联机器人拓扑结构Figure 2. Topology of 3-TRT/SPS parallel robot

2 基于方位特征理论的机构特性分析

2.1 机构的方位特征理论

基于方位特征理论的机构特性理论为：对并联机构单支链进行拓扑结构分析，再将所有支链求并集获得整机的运动特性，从而揭示机构运动的内在定律，获得整机运动的独立自由度，最后利用结构降耦和机构解耦理论分析机构耦合度[13]。

根据方位特征理论，可获得机构的POC集[14]为

(1)

(2)

式中，Mbi为第i条支链末端的POC集；Msi为第j个子SOC的VC集；Mpa为机构动平台的POC集。

由自由度和独立位移方程数的计算式可得

(3)

(4)

v=m-n+1

2.2 并联机构自由度计算

(1)支链拓扑结构。根据方位特征理论，可以获得3条TRT支链的拓扑表达式为

SOC{-Ri1⊥Ri2(‖Ri3)‖Ri4⊥Ri5-}，i=1,2,3

(5)

另一条SPS支链的拓扑表达式为

(6)

(2)选定平台上任意一点为基点O′；

(3)由式(1)可知，支链TRT末端构件的POC集为

(7)

支链SPS末端构件的POC集为

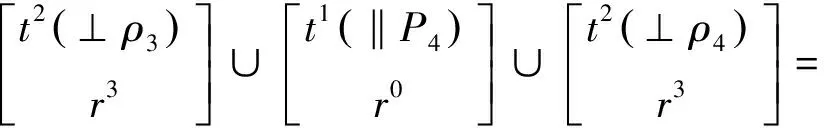
(8)

(4)确定第一个独立回路的独立位移方程数ξL1和自由度F(1-2)。将Mb1和Mb2代入式(4)可求得第一个独立回路的ξL1为

ξL1=dim{Mb1∪Mb2}=

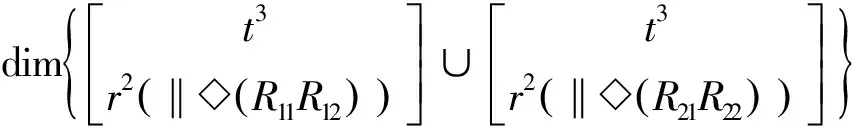
(9)

将ξL1的值代入式(3)可得第一和第二条支链组成的子并联机构DOF为

(10)

第一和第二条支链组成的并联机构动平台的POC集为

Mpa(1-2)=Mb1∩Mb2=

(11)

(5)确定第二个独立回路的独立位移方程数ξL2和自由度F(1-3)。将上述所求得的Mpa(1-2)和Mb3代入式(4)可求得第二个独立回路的ξL2为

ξL2=dim{Mpa(1-2)∪Mb3}=

(12)

将所求得的ξL1和ξL2的值代入式(3)可得，第一到第三支链组成的子并联机构DOF为

(13)

则第一到第三支链组成的并联机构平台的POC集为

Mpa(1-3)=Mpa(1-2)∩Mb3=

(14)

(6)确定第三个独立回路的独立位移方程数ξL3。同理将Mpa(1-3)和Mb4代入式(4)得第三个独立回路的ξL3为

ξL3=dim{Mpa(1-3)∪Mb4}=

(15)

(7)确定机构的自由度。将ξL1、ξL2和ξL3的值代入式(3)可得并联机构的DOF为

(16)

(8)确定并联机构平台的POC集。将Mpa(1-3)和Mb4的值代入式(2)可得式(17)。

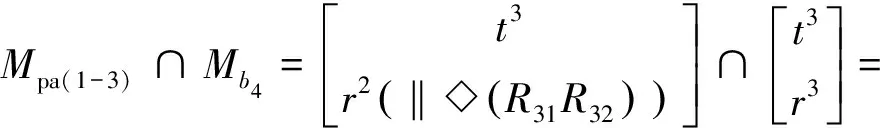
(17)

由此可知，该并联机器人的自由度为F=4，当取与静平台相连的转动副R1、R2、R3为驱动副时，该并联机器人动平台可实现3个平移和1个绕Z轴的独立转动的运动输出。

2.3 机构耦合度计算

由基于单开链(Single Open Chain,SOC)的机构组成原理可知，连接在运动链上的第j个SOCj的约束度[15]为

(18)

(19)

式中，mj为第j个SOCj的运动副数；Ij为第j个SOCj的驱动副数。

独立回路数为v的任意运动链，可视为由v个SOC一次连接而成。独立回路数为v的任意运动链又可划分为若干个最小的子运动链(Sub-kinematic Chain,SKC)，每个SKC仅含一个自由度为零的基本运动链(Basic Kinematic Chain,BCK)[16]，则对任何一个SKC有

(20)

因此，SKC耦合度k定义为式(21)。

(21)

将章节2.2求出的ξL1、ξL2和ξL3代入式(18)可得约束度分别为

(22)

将Δ1、Δ2和Δ3的值代入式(21)可得式(23)。

(23)

机构的耦合度k反映的是SKC内各回路变量之间的关联和依赖程度。k值越大，机构运动学和动力学问题求解的复杂度越高。机构的位置正解求解可转换为其各个SKC的位置求解。此外，对于k=0的SKC，其每个回路的运动量解析解都能独立求出。若k>0，则表明SKC的运动量需要多个回路方程联立求解，可用数值法或解析法求得其位置正解[12]。

3 机构的位置分析

图3 3-TRT/SPS并联机器人机构简图Figure 3.Mechanism diagram of 3-TRT/SPS parallel robot

U=U(X,Y,Z,θz)

(24)

3.1 位置正反解求解

机器人位置反解的求解过程是：已知该并联机器人的末端位姿X、Y、Z和θz，求各分支的输入角度θ1、θ2、θ3和移动副的移动长度L。

由上述所建立的动、定坐标系可知，动坐标系到定坐标系的旋转变换矩阵[T]为

(25)

可以得到与定平台平面相连的虎克铰Ci(i=1,2,3)在定坐标系中的坐标

C′i=[T]Ci+q，i=1,2,3

(26)

式中，q=[X,Y,Z]T为动坐标系原点对定坐标系的位置向量。

由此可求得该并联机器人各分支的输入角度为

θi=arctan[(C′iY-AiY)/(C′iX-AiX)]，i=1,2,3

(27)

其中

(28)

SPS分支的输入杆长为

(29)

正解的求解过程为：已知该并联机器人的各分支的输入角度θ1、θ2、θ3和移动副的移动长度L，求末端位姿X、Y、Z和θz。

联立式(26)中所求的C′1、C′2和C′33个值消去X和Y可得式(30)。

(30)

(1)当θ2≠θ3时，式(30)中的A、B和C分别为

(2)当θ2=θ3时，式(30)中的A、B和C分别为

A=r,B=-rtanθ2,C=-Rtanθ2

将式(30)中的所求得的θz代入式(28)，消去Y值可得

当θ2≠θ3时

(31)

当θ2=θ3时

(32)

此外，根据式(27)和式(28)，当i=1时可得

Y=(X+rsinθz)tanθi+rcosθz-R

(33)

将上述所求得的X和Y值同时代入式(29)中可得式(34)。

(34)

由以上的正反解计算结果可以看出该并联机器人的反解结果是唯一的，而正解相对于反解来说，结果并不唯一，且计算过程复杂多变。正解的复杂多变性，也增加了该并联机器人的轨迹规划与运动控制的难度。

3.2 机构工作空间分析

工作空间是衡量并联机器人性能的一个重要指标。并联机构的可达工作空间是指末端执行器(通常指动平台的坐标原点)可以到达的所有点的集合，这种工作空间不考虑动平台的姿态[17-19]。由章节2分析结果可知，该并联机器人的工作空间大小主要受各分支长度和运动副转角的限制。

由图3所示，分析并联机器人的3个TRT分支和1个SPS分支可知，分支的长度应满足

(35)

式中，Lmin和Lmax分别为机构实际所允许的最小和最大杆长，其中Lmax可由下式确定

(36)

运动副转角应考虑两个球铰的圆锥摆角，设驱动杆与球铰中心方向的夹角为α，球铰的最大圆锥摆角为αmax,则可有关系式为式(37)。

α≤αmax

(37)

本文采用极限边界搜索法对该并联运动机构的工作空间进行分析，首先根据杆长设定工作空间的搜索范围，基于机构位置反解式(26)，搜索所有满足约束条件式(35)和式(37)的点，这些满足条件的点所组成的三维图即为该并联机器人的工作空间。下面对该并联机器人的基本机构赋两组不同的参数值，利用MATLAB软件编程求取不同结构参数下并联机器人的工作空间。

图4 给定机构参数1时，3-TRT/SPS并联机器人在θz=0°时的工作空间Figure 4.Under mechanism parameter 1, the working space ofthe 3-TRT/SPS parallel robot at θz=0°

图5 给定机构参数1时，3-TRT/SPS并联机器人在θz=60°时的工作空间Figure 5. Under the mechanism parameter 1, the working space of the 3-TRT/SPS parallel robot at θz=60°

图4为在给定机构参数1下，3-TRT/SPS并联机器人在θz=0°时的工作空间。图5为在给定机构参数1下，3-TRT/SPS并联机器人在θz=60°时的工作空间。在θz=0°时，机构工作空间的XOZ截面图和YOZ截面图分别如图6(a)和图6(b)所示。

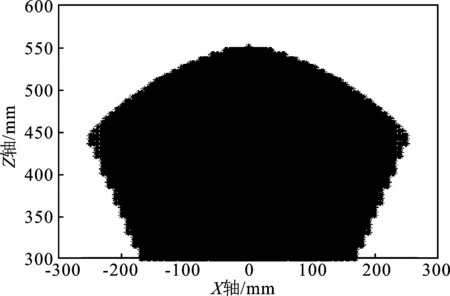
(a)

(b)图6 给定机构参数1时，3-TRT/SPS并联机器人在θz=0°时的工作空间在XOZ和YOZ平面的投影图(a)给定机构参数1时XOZ平面投影 (b)给定机构参数1时YOZ平面投影Figure 6. Under the mechanism parameter 1, the projection diagram of the working space of the 3-TRT/SPS parallel robot on the XOZ and YOZ planes when θz=0°(a)XOZ planar projection under the mechanism parameter 1 (b)YOZ planar projection under the mechanism parameter 1

图7 给定机构参数2时，3-TRT/SPS并联机器人在θz=0°时的工作空间Figure 7.Under the mechanism parameter 2, the working space of the 3-TRT/SPS parallel robot at θz=0°

图8 给定机构参数2时，3-TRT/SPS并联机器人在θz=60°时的工作空间Figure 8.Under the mechanism parameter 2, the working space of the 3-TRT/SPS parallel robot at θz=60°

(a)

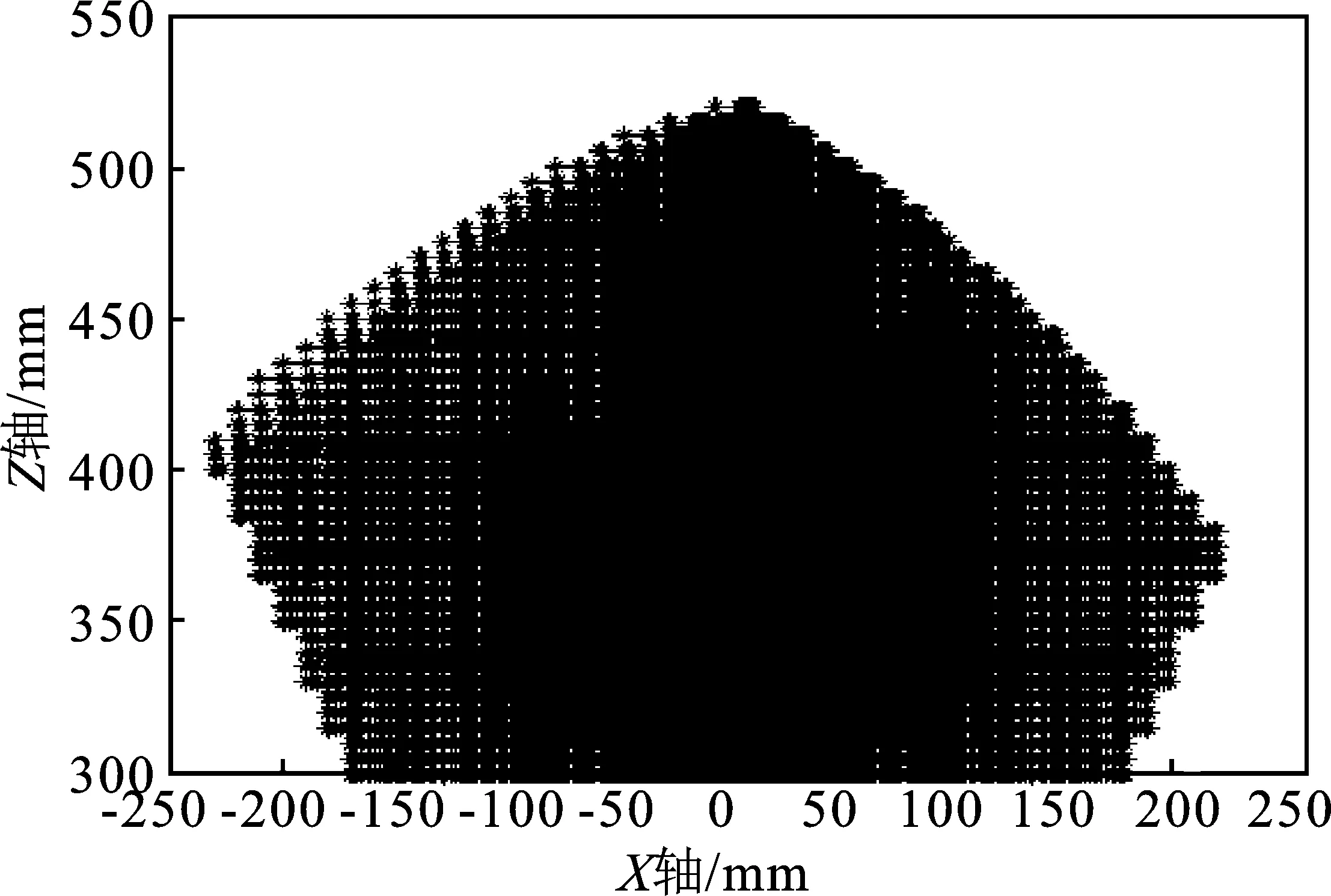
(b)图9 给定机构参数2时，3-TRT/SPS并联机器人在θz=0°时的工作空间在XOZ和YOZ平面的投影图(a)给定机构参数2时XOZ平面投影 (b)给定机构参数2时YOZ平面投影Figure 9.Under the mechanism parameter 2, the projection diagram of the working space of the 3-TRT/SPS parallel robot on the XOZ and YOZ planes when θz=0°(a)XOZ planar projection under the mechanism parameter 2 (b)YOZ planar projection under the mechanism parameter 2

由图4和图5可以看出，在动、静平台尺寸相对较小的情况下，该并联机器人的工作空间为上部接近半球体，中间鼓的形状。其大小与θz值有关，θz值越大机器人工作空间的体积越小，体积大小随θz值变换幅度相对较小。在θz=0时，该并联机器人的工作空间关于XZ平面对称，但是不关于YZ平面对称。

由图7和图8可以看出，在动、静平台尺寸相对较大的情况下，该并联机器人的工作空间为上部尖，中间鼓的形状。其大小与θz值有关，θz值越大机器人工作空间的体积越小，体积大小随θz变换幅度相对较大。在θz=0时，该并联机器人的工作空间同样是关于XZ平面对称，但是不关于YZ平面对称。

为了更好地表明3-TRT/SPS并联机器人使用范围的广阔性，现将3-TRT/SPS并联机器人的工作空间和3PTT并联机器人的工作空间进行对比验证。3PTT并联机器人的三维模型如图10所示。3-PTT并联机器人有3条对称分布的PTT支链，PTT支链的两端是虎克铰，中间是由短杆和长杆组成的平行四边形机构。PTT支链一端通过丝杠滑块机构与竖直的固定型材相连；另一端通过平行四边形机构与运动平台相连。3-PTT并联机器人是三自由度机器人，输出参数是动平台的3个位姿，输入参数是3个丝杆滑块机构的滑块移动距离。3PTT并联机器人的动、定平台外接圆半径分别为r和R，由短杆和长杆组成的平行四边形机构的长为L。

图10 3-PTT并联机器人三维模型Figure 10.3D model of 3-PTT parallel robot

给定3-PTT并联机器人的基本机构参数为：r=200 mm，R=400 mm，L=350 mm。利用MATLAB软件编程，得到3-PTT并联机器人的三维工作空间如图11所示。

图11 3-PTT并联机器人的工作空间Figure 11. Working space 3-PTT parallel robots

由图11可以看出3-PTT并联机器人的工作空间是一个上半部分为椭球形，下半部分为圆柱形的形状。该工作空间关于XZ平面对称，也关于YZ平面对称。

由图7、图8和图11可以看出，在机器人机构参数大致相同的情况下，3-PTT并联机器人的工作空间是一个固定的形状，而3-TRT/SPS并联机器人的工作空间大小随θz的值变化而发生变化。该结果说明3-TRT/SPS并联机器人相对于3-PTT并联机器人有更广阔的应用环境。

4 结束语

本文以3-TRT/SPS并联机器人为研究对象，首先运用方位特征理论分析该并联机器人的结构特征，并求解其自由度，运用解析法推导了该并联机器人运动末端的正反解。然后，采用极坐标搜索法对并联机器人的工作空间分析，并使用MATLAB软件绘制出并联机器人的工作空间。通过对不同结构参数的3-TRT/SPS并联机器人的工作空间对比分析，得出在其他参数相同情况下，并联机器人的工作空间变化幅度随动、静平台的尺寸而变化。此外，本文通过相同结构参数的3-TRT/SPS并联机器人和3-PTT并联机器的工作空间对比分析，得出在参数相同情况下，3-PTT并联机器的工作空间是一个固定的形状，而3-TRT/SPS并联机器人的工作空间随θz的值变化而发生变化。这些结果也为后续的工业生产加工提供了一定的参考。