焊接残余应力对对接接头疲劳裂纹扩展的影响

顾颖，冯倩，任松波，孔超，古松

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2.工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621010)

焊接残余应力是自平衡应力，其在焊缝区表现为达到或超过材料屈服强度σy的拉应力[1]，在远离焊缝的区域为较小的压应力。这意味着焊接结构在未受任何外载的情况下，局部就已经存在高达材料屈服强度的拉应力状态。研究表明[2]，由于高值焊接残余拉应力的存在，即使在纯压循环荷载下，焊接接头也可能出现裂纹萌生与扩展。对此，FISHER[3]对大尺寸焊接构件进行了大量的疲劳试验，发现存在于焊缝区的高值残余拉应力是导致疲劳强度降低主要因素。相对于疲劳试验，数值模拟的方式更为方便。当前，采用数值模拟来研究焊接残余应力对疲劳性能影响的方法主要是基于断裂力学，通过有效应力比Reff，有效应力强度因子范围ΔKeff来计入焊接残余应力对疲劳裂纹扩展速率da/dN的影响[4−7]。该方法一般先通过有限元法或测试获得焊接残余应力，再采用权函数法[8]、虚拟裂纹闭合法[4]或J积分法[9]计算焊接残余应力引起的应力强度因子Kres。求得Kres后，就可以采用考虑应力比影响的疲劳裂纹扩展公式求解da/dN。常见的公式有Walker公式、Harter T方法、NASGRO公式等[10]。该方法一般将焊接残余应力作为初始状态或直接拟合为位置的函数，并假定在裂纹扩展过程中保持不变，以此来计入其对da/dN的影响。然而，实际上焊接残余应力在疲劳开裂过程中会发生重分布[6−7]，它会因裂纹的扩展而释放，因裂尖的塑性变形而松弛[11]。当然若事先知道焊接残余应力随裂纹长度a的变化，也可以在拟合函数引入a来计入其对da/dN的影响。瞿伟廉等[6]采用此方法，借助TERADA[7]提出的焊接残余应力重分布模型，成功地预测了对接接头试件的疲劳寿命。由于焊接残余应力主要表现为纵向应力(平行于焊缝)，因此当前的研究大多忽略横向应力(垂直于焊缝)，仅针对纵向残余应力，研究其对疲劳寿命的影响。然而现实中，裂纹面沿焊缝，特别是沿焊趾或焊根萌生或扩展的现象更为普遍。对于这种裂纹面平行于焊缝的情况，纵向的焊接残余应力并未在裂纹面产生牵引力，并不能使裂纹面张开或闭合。此外，若焊接残余应力是通过数值模拟获得，在考虑焊接残余应力的疲劳裂纹扩展模拟中还存在如何将计算的残余应力映射到疲劳裂纹扩展模型中去的技术问题。针对上述问题，本研究以平板对接焊为例，首先采用热弹塑性有限元法获得焊接残余应力，然后结合计算机图形学和等参元逆变换提出了焊接残余应力映射技术，并基于该技术将计算的焊接残余应力映射到裂纹扩展模型中去。在疲劳裂纹扩展模型中，以疲劳裂纹扩展的模拟来自动计入焊接残余应力的重分布效应，以焊接残余应力引起的应力强度因子Kres，基于NASGRO方程来计入焊接残余应力对疲劳裂纹扩展速率的影响。

1 焊接残余应力数值模拟

1.1 焊接数值模拟模型

采用ANSYS软件，基于热弹塑性有限单元法，以平板对接焊为例进行焊接数值模拟，模型尺寸如图1所示。图中，xyz坐标系原点位于起弧点；x轴垂直于焊缝；z轴位于焊缝中心线Weld Line上，指向焊接前进方向。模型采用Q345钢材的热力学参数，按文献[1]取值。焊接熔敷金属的填充过程采用“生死单元”模拟。焊接热源选用双椭球热源模型来模拟 ，模型中参数取值同文献[1]。

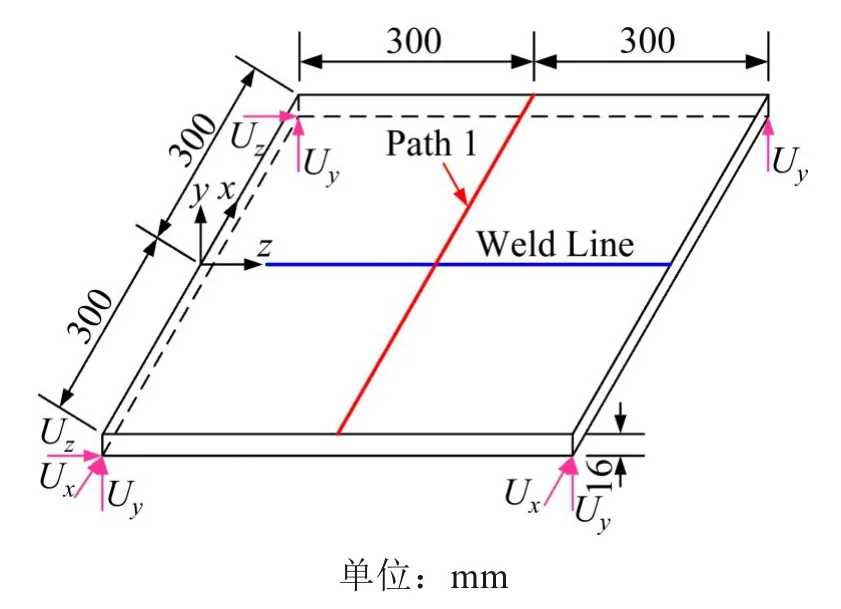
图1 平板对接焊模型尺寸Fig.1 Dimension of the butt weld for numerical case study

焊接温度场采用SOLID70单元模拟，节点自由度为温度。为减小单元数目并保证计算精度，单元网格采用六面体划分，划分尺寸在焊缝附近为2 mm，该尺寸由小到大逐步过渡到远离焊缝的20 mm。焊接温度场模拟边界条件主要包括：环境温度、工件表面对流换热及辐射传热。本研究环境温度取室温25℃，并假定在焊接过程中不发生变化。对流与辐射传热采用式(1)所示的牛顿冷却公式计算：

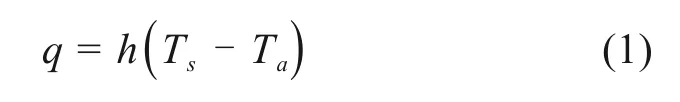
式中：q为热流密度，W/m2；Ts为工件表面温度；Ta为环境温度，取25℃；h为综合考虑对流、辐射传热的换热系数，W/(m2•℃)，按式(2)取值[13]。

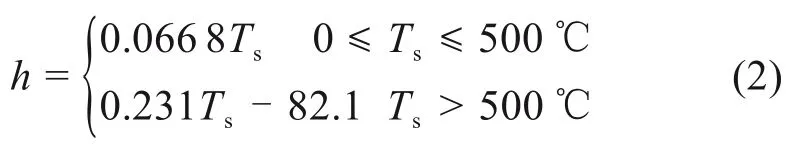
焊接温度场计算完成后，用ETCHG命令将温度分析SOLID70单元转换为力学分析SOLID185单元，再读入温度场计算结果进行力学分析。力学分析采用的单元网格同温度场分析，采用的边界条件如图1所示，图中Ux，Uy，Uz分别表示沿x，y，z方向的平动自由度约束。

1.2 焊接残余应力计算结果

图2所示为Path 1(见图1)路径上的纵、横向焊接残余应力随x轴的变化。从图2可以看出，焊缝附近区域存在高达材料屈服强度(σy=345 MPa)的纵向残余拉应力σz，而在远离焊缝的位置，σz为较小的压应力。焊接横向残余应力σx在宽度方向呈M型分布，σx在焊缝中心出现压应力峰值(−59.7 MPa)，且随着远离焊缝约30 mm的位置出现拉应力峰值(96.9 MPa)。该计算结果与文献[5]的16 mm厚平板对接焊的焊接残余应力测试结果吻合。

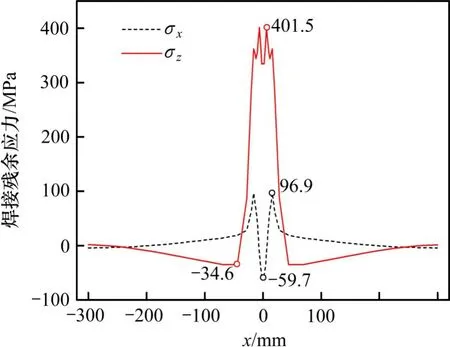
图2 Path 1路径上焊接残余应力随x的变化Fig.2 Variation of WRSs in Path 1 with x-axis

2 应力映射技术

设裂纹扩展分析模型(新模型)中存在一节点P，现需要根据P在焊接数值模拟模型(旧模型)中的相对位置，求出该节点对应的焊接残余应力状态Sp。这涉及到2个技术问题：一是判断节点P在旧模型中属于哪一个单元或位于哪一个单元的内部；二是根据其所属单元的各节点应力，通过形函数插值计算出节点P所对应的Sp。对于前者需要用到点与多面体的位置关系算法[14]，对于后者涉及到等参单元的逆变换算法[15]。本文结合这2种算法提出焊接残余应力映射技术，并加以验证。

2.1 点与单元空间位置关系的判断

设新模型中任意一节点P，其在旧模型中的坐标与新模型保持一致，均为(xp,yp,zp)。在旧模型中，假设该节点附近存在某单元E，其任意面A的外法线向量为，如图3所示。

图3 点与单元空间位置关系示意图Fig.3 Schematic diagram of position relationship between an point and element

假设面A上有任意点P'，P'也可以是位于面A且属于单元E的节点，其到点P的向量为，则与数量积表示为：

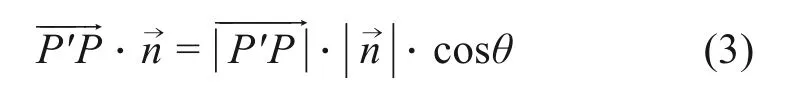
式中：θ为向量角。由于均大于等于0，因此可根据的符号来判断点P与面A的位置关系[14]，如式(4)所示。

若对于单元E上的所有面均满足时，则可判定点P位于单元E的内部。此时便可根据单元E各节点的应力状态，利用形函数插值得到点P对应的焊接残余应力状态Sp。

2.2 等参单元逆变换算法

在三维等参有限元分析中，有坐标变换[15]：

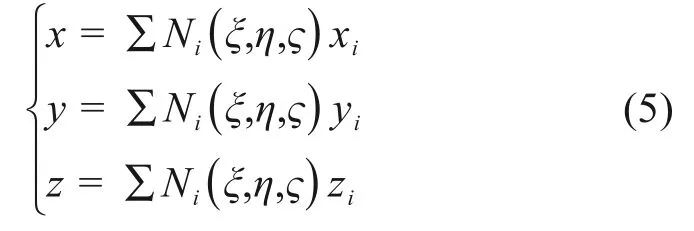
式中：ξ，η，ζ为单元局部坐标系下的坐标；xi，yi，zi为节点i在整体坐标系中的坐标；Ni为插值函数。焊接数值模拟一般采用8节点六面体线性单元，其插值函数为：

式中：ξi，ηi，ζi为节点i在局部坐标系下的坐标。

式(5)可简化地写成：

将上式在点(x0,y0,z0)按泰勒级数展开[14]，且忽略高阶项得：

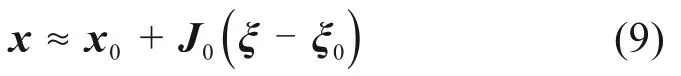
对式(9)两端乘以J0的逆矩阵，整理得：

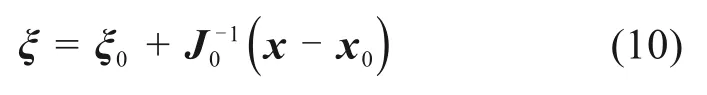
由上式可得到坐标(ξp,ηp,ζp)的迭代公式：

式中：n为迭代次数；ξn为ξp的第n次迭代近似值。按式(11)反复迭代，直至≤ε时，ε是人为设定的微小量，可以认为点P的局部坐标近似地求出，即：

获得点P的局部坐标(ξp,ηp,ζp)后，就可根据式(13)利用点P所属单元E的各节点应力状态插值得到点P所对应的焊接残余应力Sp。

2.3 应力映射技术验证

为验证应力映射技术是否有效，同时考虑到焊接纵向残余应力远大于横向残余应力，故提取垂直于焊缝的Path 1路径上映射前后的σz进行对比，如图4所示。从图中可以看出，映射后的σz可以捕捉到原应力分布的特征，且在数值上也较为吻合，映射前后σz随x的变化曲线基本重合。由此可以说明本文提出的焊接残余映射技术是有效的。

图4 应力映射前后焊接纵向残余应力σz对比Fig.4 Comparison of longitudinal WRSs before and afterstress mapping

3 疲劳裂纹扩展模拟

3.1 裂纹扩展速率模型

基于线弹性断裂力学，考虑焊接残余应力的疲劳裂纹扩展模拟可根据叠加原理，通过有效应力比Reff来计入焊接残余应力的影响。考虑焊接残余应力的作用，应力强度因子ΔKeff范围及有效应力比Reff定义为：

式中：Kapp,max，Kapp,min分别为外载引起的应力强度因子的最大、最小值；Kres是焊接残余应力作用下的应力强度因子。

从式(14)～(15)可以看出，由于焊接残余应力的存在，应力比会发生改变，而应力强度因子范围跟无焊接残余应力的情况一致。当获得Rres，ΔKeff以后，便可以通过计入R和ΔK影响的裂纹扩展模型求解da/dN，如NASGRO[10]方程。由于NASGRO方程考虑了裂纹闭合效应，也计入了近门槛区、近断裂区疲劳裂纹扩展特性，因此本研究选用NASGRO方程来计算裂纹扩展速率，见式(16)。

式中：Kc为断裂韧性；ΔKth为疲劳裂纹扩展门槛值；Kmax为裂纹强度因子最大值，考虑焊接残余应力影响时，Kmax=Kapp,max+Kres；C与n为Paris公式常数；p、q分别是为考虑近门槛区、近断裂区疲劳裂纹扩展特性而定义的常数；f为裂纹闭合效应函数。NASGRO公式中的参数根据文献[10]取值，见表1。

表1 NASGRO方程参数Table 1 Parameters in NASGRO equation

3.2 初始裂纹设置

为探究不同位置的焊接残余应力对疲劳性能的影响，本研究设置4种初始裂纹：Crack 1，Crack 1′，Crack 2及Crack 2′。这4种初始裂纹均为椭圆形，如图5所示，其长半轴半长c为4 mm，短半轴半长a为2 mm。图中“Cor坐标轴”为沿裂纹前缘的归一化坐标轴，在裂纹前缘图示左端点Cor=0，在中点Cor=0.5，右端点Cor=1。如图5所示，Crack 1与Crack 1′裂纹面垂直于焊缝，分别位于焊接残余应力的拉应力与压应力区；Crack 2与Crack 2′裂纹面平行于焊缝。所定义的4种裂纹均假定沿最大环向拉应力作用面的方向扩展。

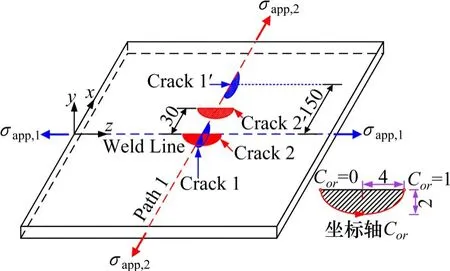
图5 初始裂纹设置示意图Fig.5 Schematic diagrams of initial cracks

裂纹扩展有限元模型采用20节点SOLID186单元建立。由于裂纹前缘的应力与应变具有奇异性，所以裂纹前缘附近单元采用在1/4处有中间节点的奇异单元模拟，网格尺寸不大于0.1 mm。在远离裂纹前缘的单元网格控制尺寸为10 mm。为了使研究结果具有一定的代表性，施加于模型远端的外载σapp参考国标GB50017—201716]规定的容许应力幅取值，即σapp=120 MPa，以R=0.1循环。对于所定义的4种初始裂纹，外载均沿垂直于裂纹面的方向施加。具体地讲，对于Crack 1和Crack 1′，外载σapp,1在模型右端面(z=600 mm)施加，同时在左端面(z=0 mm)约束z向的平动自由度，并在坐标原点约束x，y，z3个方向的平动自由度，以限制刚体位移。Crack 2和Crack 2′外载σapp,2的施加与边界条件按照类似方式定义。

4 结果与分析

4.1 焊接残余应力对应力强度因子的影响

Crack 1与Crack 1′主要用于考察焊接纵向残余应力σz对裂纹扩展的影响。Crack 1位于高值残余应力(拉)的焊缝区，Crack 1′位于远离焊缝150 mm的低值残余应力区(压)。应力强度因子沿Crack 1与Crack 1′裂纹前缘的变化如图6所示。

图6 应力强度因子沿Crack 1与Crack 1′裂纹前缘的变化Fig.6 Variation of stress intensity factor along fronts of cracks 1 and 1′

如图6(a)所示，对于Crack 1，焊接残余应力引起的应力强度因子Kres在裂纹前缘上均为正，且在数值上大于外载产生的应力强度因子Kapp，致使叠加后的应力强度因子Ktol远大于Kapp，前者约是后者的4倍。说明对于Crack 1，焊接残余应力的存在会极大地加速裂纹的萌生与扩展。对于Crack 1′，Kres在裂纹前缘上均为负值(图6(b))，其与Kapp叠加后的应力强度因子Ktol小于Kapp，前者约是后者的0.8倍。说明对于Crack 1′，焊接残余应力会抑制裂纹的扩展。值得注意的是，由高达材料屈服强度的焊接残余应力引起的K已经达到795.1 MPa⋅mm0.5，见图6(a)。此时，若假设有一外载为压缩荷载，其应力强度因子为-500 MPa⋅mm，并按R=0循 环，则ΔKeff=(0+795.1)-(-500+795.1)=500 MPa⋅mm0.5，该值已大于常见结构钢的疲劳裂纹扩展门槛值。由此说明，由于焊缝区存在较高的焊接残余拉应力，造成了即使外载为纯压荷载，材料也可能出现疲劳问题，此现象也在疲劳试验中得到了证实[2−3]。

Crack 2与Crack 2′的裂纹面平行于焊接方向，主要用于考察焊接横向残余应力σx对疲劳裂纹扩展的影响。Crack 2位于焊缝区，Crack 2′位于远离焊缝中心30 mm的位置。对于Crack 2，焊接残余应力引起的应力强度因子Kres在裂纹前缘为负(见图7(a))，与Kapp叠加后的应力强度因子Ktol小于Kapp，前者是后者的0.56～0.75倍。说明对于Crack 2，焊接残余应力的存在会抑制裂纹的扩展。对于Crack 2′，Kres在裂纹前缘均为正(见图7(b))，与Kapp叠加后的应力强度因子Ktol大于Kapp。前者约是后者的1.2倍。说明对于Crack 2′，焊接残余应力的存在会促进裂纹的扩展。

图7 应力强度因子沿Crack 2与Crack 2′裂纹前缘的变化Fig.7 Variation of stress intensity factor along fronts of cracks 2 and 2′

4.2 焊接残余应力对疲劳寿命的影响

为了能获得足够多的数据点，以清楚地显示各裂纹间裂纹长度与循环次数的差异，本研究以初始裂纹深度为2 mm，其沿板厚扩展至6.2 mm时的外载循环次数N来反映焊接残余应力对疲劳寿命的影响。图8所示为各裂纹在焊接残余应力影响下的裂纹长度a与循环次数N的关系曲线，即a-N曲线。图中“Reference curve”为参考曲线，是Crack 1在无焊接残余应力情况下的a-N曲线，其余裂纹无残余应力下的a-N曲线与之相近。从图8可以看出，焊接残余应力对焊缝区的Crack 1裂纹的da/dN影响最大，焊接残余拉应力的存在会极大地加速裂纹的扩展。Crack 2与Crack 2′也位于残余拉应力区，相对于无残余应力情况，其裂纹扩展速率也出现了增大；Crack 1′位于残余压应力区，其裂纹扩展速率小于无残余应力的情况。

图8 裂纹长度与荷载循环次数的关系曲线Fig.8 Relation curves between crack length and load cycles

值得说明的是对于本算例16 mm钢板，计算结果显示焊接残余应力沿板厚基本保持不变，这个结论与文献[5]实测结果一致。因此，为定量分析其对疲劳寿命的影响，以裂纹扩展路径上的焊接残余应力均值σave来表征各裂纹对应的焊接残余应力水平。

表2所列即为各裂纹在有、无焊接残余应力情况下，裂纹在深度方向从2.0 mm扩展至6.2 mm的外载循环次数。综合图8与表2所列数据可以发现，对于所定义的4种裂纹，裂纹前缘中点的焊接残余应力σave由大到小(计入正负号)依次为Crack 1，Crack 2，Crack 2′，Crack 1′，其裂纹扩展速率也是按该顺序由快到慢变化的。通过表2可以看出，Crack 1′裂纹前缘中点的焊接残余应力均值σave仅为-0.07σy，但却将材料的疲劳寿命提高了76.6%，说明即使是很小的焊接残余压应力也能显著地提高材料的疲劳寿命。类似地，Crack_2′的焊接残余应力也很小，仅为0.06σy，但其对疲劳寿命的影响却达到了-27.9%，说明即使是很小的焊接残余拉应力也可能显著地降低材料的疲劳寿命。

对比表2中Crack 1与Crack_2′的相关数据可以发现，Crack 1对应的焊接残余应力是Crack 2′的19.7倍(前者403.4 MPa，后者20.5 MPa)，但其对疲劳寿命的影响仅是Crack 2′的2.1倍(前者-59.1%，后者-27.9%)，说明焊接残余拉应力对疲劳寿命的降低程度并不与其大小成正比，它会随着焊接残余应力的增大而增大，但增大的比例会随着焊接残余应力的增大而显著减小。这主要是因为焊接残余应力为拉时取值为正，根据式(12)和式(13)，它只会改变应力比R，而不会改变应力强度因子范围ΔK，因而它只能通过Reff间接影响疲劳寿命。

表2 焊接残余应力与对疲劳寿命对照Table 2 Comparison of WRS and fatigue life

对比表2中Crack 1′和Crack_2′的数据可以发现，Crack_1′的焊接残余应力(-24.7 MPa)与Crack 2′的应力(20.5 MPa)在大小上相近，在符号上相反。但前者对疲劳寿命的影响程度是后者的2.7倍，前者将疲劳寿命提高了76.6%，后者降低了27.9%。据此可以推测，焊接残余应力对疲劳寿命的影响大小还与其符号有关，为压的残余应力对疲劳寿命的提高程度要比相同大小的拉应力的降低程度大。如本算例中前者就比后者大了1.7倍。这主要是因为当焊接残余应力为负值时，它可能会直接降低应力强度因子范围ΔK，从而使ΔK更接近于甚至低于疲劳裂纹扩展门槛值ΔKth，此时疲劳裂纹的扩展就会显著的降低。以例说明，假设外载产生的应力强度因子Kapp=400 MPa⋅mm0.5，以R=0.1循环，现有2种情况，一是残余应力为拉应力，假设其产生的应力强度因子Kres=80 MPa⋅mm0.5，由此计算的应力强度因子范围为ΔK1=(400+80)-(400×0.1+80)=360 MPa⋅mm0.5，有效应力比Reff_1=0.250；二是焊接残余应力为压应力，相应的Kres=-80 MPa⋅mm0.5，ΔK2=(400-80)-max(400×0.1-80,0)=320 MPa⋅mm0.5，小于ΔK1，有效应力比Reff_2=-0.125也小于Reff_1。由此可见，相对于焊接残余应力为拉应力的情形，焊接残余应力为压时的有效应力比和应力强度因子范围都有可能降低，而这两者的降低均会导致疲劳裂纹扩展速率的减小，从而大幅地提高疲劳寿命。

5 结论

1)基于计算机图形学和等参单元逆变换提出的应力映射技术能有效地将计算的焊接残余应力映射到疲劳裂纹扩展模型中去。经对比，不同模型间映射前后应力状态吻合较好。

2)即使是很小的焊接残余拉应力也可能对材料疲劳寿命造成显著的降低，本算例不到10%σy的残余拉应力，将疲劳寿命降低了25%以上。因此，针对典型焊接疲劳细节，宜尽可能的完全消除残余拉应力或通过表面处理直接将拉应力转换为压应力。

3)即使是很小的焊接残余压应力也可能显著地提高材料的疲劳寿命，本算例不到10%σy的残余压应力，将疲劳寿命提高了75%以上。因此，针对典型疲劳构造细节，可通过喷丸、超声冲击等措施给材料表面预制一定的压应力以提高疲劳强度，而且无需以生成高值残余压应力为目的，只需根据构造细节与外载特性，预制出能使ΔK小于或接近于疲劳裂纹门槛值ΔKth的压应力就可有效地改善材料疲劳性能。

4)焊接残余拉应力对疲劳寿命的降低程度会随着应力的增大而增大，但增大的比例会随着应力值的增大而显著的减小。焊接残余应力对疲劳寿命的影响大小还与其符号有关，焊接残余压应力对疲劳寿命的影响要比同值的拉应力的影响大。这主要是因为焊接残余应力为拉时取值为正，它只会改变应力比R，而不会改变应力强度因子范围ΔK，因而它只能通过应力比间接影响疲劳寿命；而焊接残余应力为压时，在降低应力比R的同时还可能直接降低应力强度因子范围ΔK，而这两者的降低均会导致裂纹扩展速率的减小，从而大幅地提高疲劳寿命。