基于列车运行仿真和SVR组合的地铁新线牵引能耗预测方法

周姗姗，柏赟，袁博，汪茜，李佳杰

(北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

随着全国各大城市地铁新线的持续开通运营，地铁系统的节能降耗日益重要。新线规划设计的优劣和列车选型直接影响着线路牵引能耗水平，进而影响城市轨道交通系统总电耗与成本。因此，有必要研究城市轨道交通新线牵引能耗预测方法，从节能角度为新线规划设计方案选取及列车选型提供参考。牵引能耗的影响因素主要包括线路条件、列车属性、行驶速度及操纵策略等[1−4]。此外，天气、运营组织方案、客流等扰动因素也会影响总牵引能耗。既有研究大多采用仿真方法或历史数据刻画能耗与各因素的特征关系，进而预测列车牵引能耗。前者通过分析列车运行受力情况，构建列车动力学模型，在此基础上计算牵引能耗。该类研究包括单列车运行仿真及多列车运行仿真。其中，单列车仿真系统无法考虑多列车之间的再生能传输过程，能耗计算存在偏差[5−6]。而多列车仿真系统虽可以刻画列车间再生能传递过程，但由于供电参数标定困难、仿真耗时较长，很少应用于地铁新线的能耗预测[7−8]。除仿真方法外，部分学者也通过构建大数据模型来预测列车牵引能耗。陈垚等[9]基于SVR模型，以月均最高气温、辅助设备功率、日均客运周转量、全日走行公里、最小发车间隔、有效间隔占比为输入预测既有线未来月度牵引能耗。吕欢欢等[10]采用支持向量回归及随机森林回归方法对既有线牵引能耗进行预测。该类方法可根据大量既有能耗数据，较为准确地刻画能耗与影响因素的非线性特征关系，实现既有线能耗预测。但对于新线而言，线路条件、列车性能可能与既有线存在较大差异，且难以用简单的参数如平均站间距、平均坡度、最大功率来刻画线路条件和列车属性对能耗的影响。因此，既有的大数据模型在预测地铁新线能耗时存在较大偏差。本文将仿真方法与数据预测方法的优点相结合，提出基于列车运行仿真与支持向量回归(SVR)组合的地铁新线车公里牵引能耗预测方法，同时考虑线路条件、列车属性、操纵策略以及天气、客流、运营方案等扰动因素，实现地铁新线牵引单耗的精确预测。

1 预测方法框架

本文所提出的预测方法共包含列车运行仿真刻画和支持向量机预测2个步骤，如图1所示。

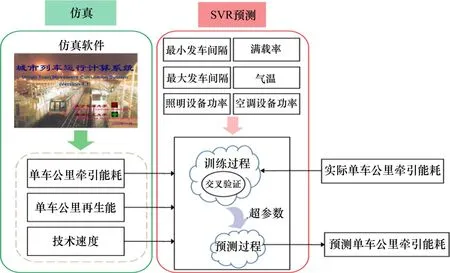
图1 预测方法框架Fig.1 Prediction method framework

步骤1：仿真过程。

对单列车运行过程进行仿真，输入线路条件、列车属性等相关参数，即可得到列车运行的单车公里牵引能耗、单车公里再生能产生量及技术速度3个指标，其将作为下一步支持向量机预测的输入。相较于采用平均坡度、平均站间距等值刻画线路条件的影响，其基于物理模型求解单列车运行仿真过程的实时能耗，可反映部分牵引能量消耗的内在机理。

步骤2：支持向量机预测过程。

1)输入输出变量选取。由于单列车运行仿真过程未刻画再生能耗和辅助能耗，在该步骤中添加最小发车间隔、最大发车间隔、满载率、气温及照明设备功率、空调设备功率指标，与上一步仿真所得的单车公里牵引能耗、单车公里再生能产生量及技术速度共同作为第2步SVR的输入变量。输出变量则选取为单车公里牵引能耗。

2)训练过程。通过提取训练样本中输入变量和输出变量的特征关系，训练SVR模型，并采用交叉验证方法及遗传算法对模型超参数进行寻优。本文中训练样本为既有线，预测样本为新线。

3)预测过程。在已知新线输入变量的条件下，基于训练所得的SVR模型，可实现新线单车公里牵引能耗预测。

2 列车运行仿真

单列车运行仿真系统可模拟列车运行过程，进而计算列车运行实时能耗。列车运动方程为[11]：

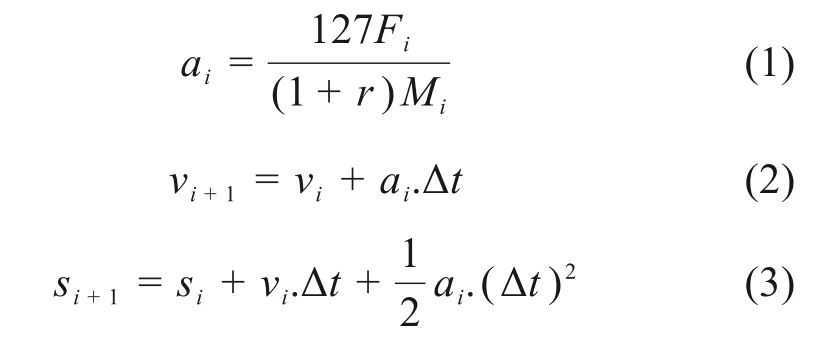
式中：i代表仿真时间步长；ai，vi，si分别代表第i个仿真步长初的列车加速度、速度以及位置。r代表列车回转质量系数，取0.06。Mi代表列车牵引重量，由列车自重和乘客总重共同构成。Δt为步长间隔，取0.5 s。Fi代表列车运行过程中所受合力，其可被定义为：

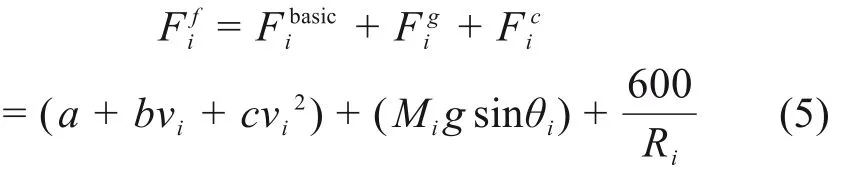
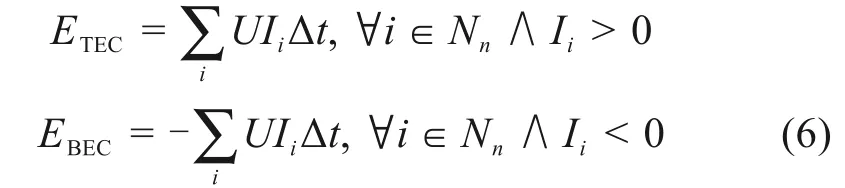
式中：U代表受电弓处网压。Ii代表第i个仿真步长下的电流，由列车有功/制动电流特性曲线和当前速度决定。当列车处于牵引状态时，Ii>0，处于制动状态时，Ii<0。Nn代表列车从起点运行至终点包含的所有步长集合。

最终，可得单列车全线运行时单车公里牵引能耗ETEE，单车公里再生能产生量EBEE及技术速度V为：

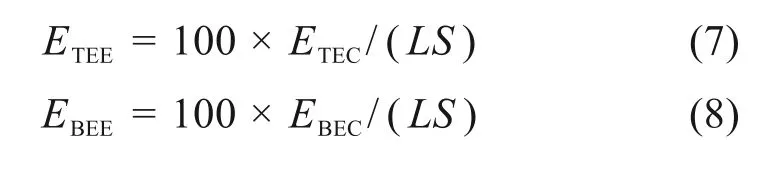
式中：L代表列车走行公里，其等于线路长度。S代表列车编组数量；T代表列车从起点站运行至终点站不包括停站时分所耗总时长。

列车全线运行时有上下行之分，上下行线路条件不同，会导致单车公里牵引能耗、单公里再生能产生量及技术速度发生变化。由于列车多为成对运行，上下行开行列车数量相等，本文采用上下行单车公里牵引能耗、单车公里再生能产生量及技术速度平均值作为支持向量机输入变量。

3 SVR预测

支持向量机[12]是一种典型的机器学习方法，在处理非线性问题上具有独特的优势。其核心思想是将训练样本(Xi,Yi)映射到高维空间X→φ(X)实现线性回归，SVR方程为：

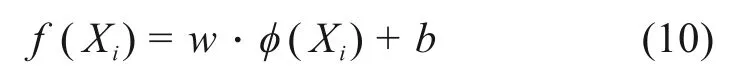
式中：w为权值向量，b为偏置值。Yi代表训练样本i的地铁牵引单耗，Xi代表第i个样本中的输入变量，为影响输出变量Yi的各因素取值。

支持向量回归的最终目的是求解得到w与b，使得样本与回归曲线的误差最小。基于结构风险最小化原则，该优化问题可构建为：

式中：ξ和ξ*代表松弛变量，C为惩罚因子，ε代表不敏感损失系数，即如果样本点到回归平面的距离小于ε，则损失为0。SVR的损失函数[13]为：

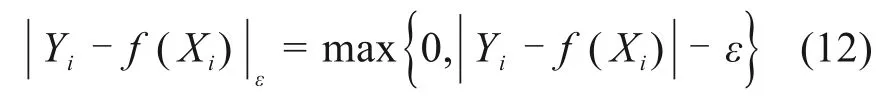
对于式(11)所示的凸二次规划问题，可引入拉格朗日乘子α及α*，将其转变为对偶问题进行求解：

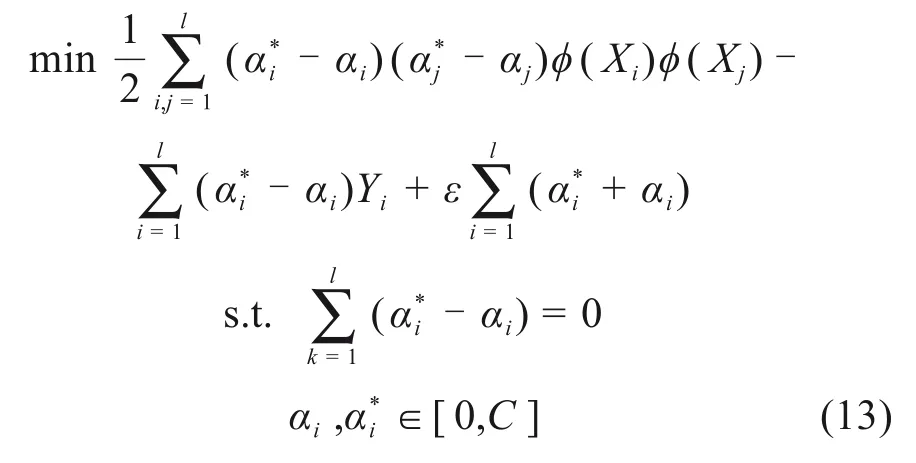
其中，权值向量w为：

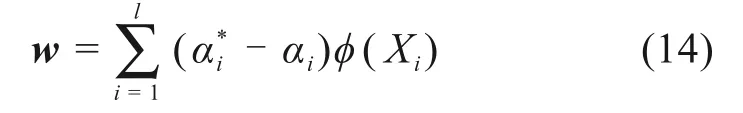
则SVR模型可被表示为：

为简化优化问题维度，引入满足Mercer[14]条件K(Xi,X)=φ(Xi)φ(X)的核函数。此时，SVR模型可表示为：

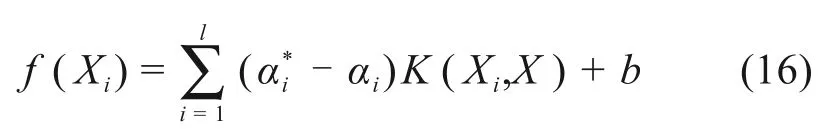
核函数可将模型由低维映射到高维，使得模型在高维中实现回归。本文引入高斯核函数，其可被定义为：

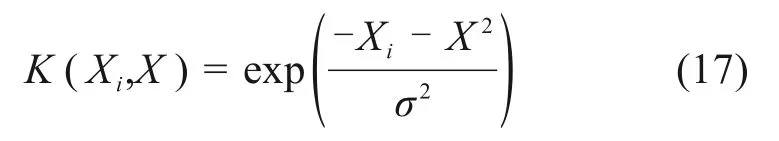
式中：σ2为核函数宽度。

因此，通过挑选合适的惩罚因子C，不敏感损失系数ε以及核函数宽度σ2可实现支持向量机模型训练。其中，超参数C，ε及σ2影响模型训练效果。惩罚因子C代表对训练误差大于ε的样本的惩罚，C越大，训练样本的准确性越高，模型的泛化能力越低。ε影响支持向量的数目，ε越大，支持向量数越少，模型可能过于简单，学习精度低。σ2决定数据映射到新的特征空间的分布形态，σ2越小，宽度越小，训练准确率高，但模型的泛化能力差，容易过拟合。

本文采用遗传算法对超参数C，ε及σ2进行寻优，其流程如图2所示。

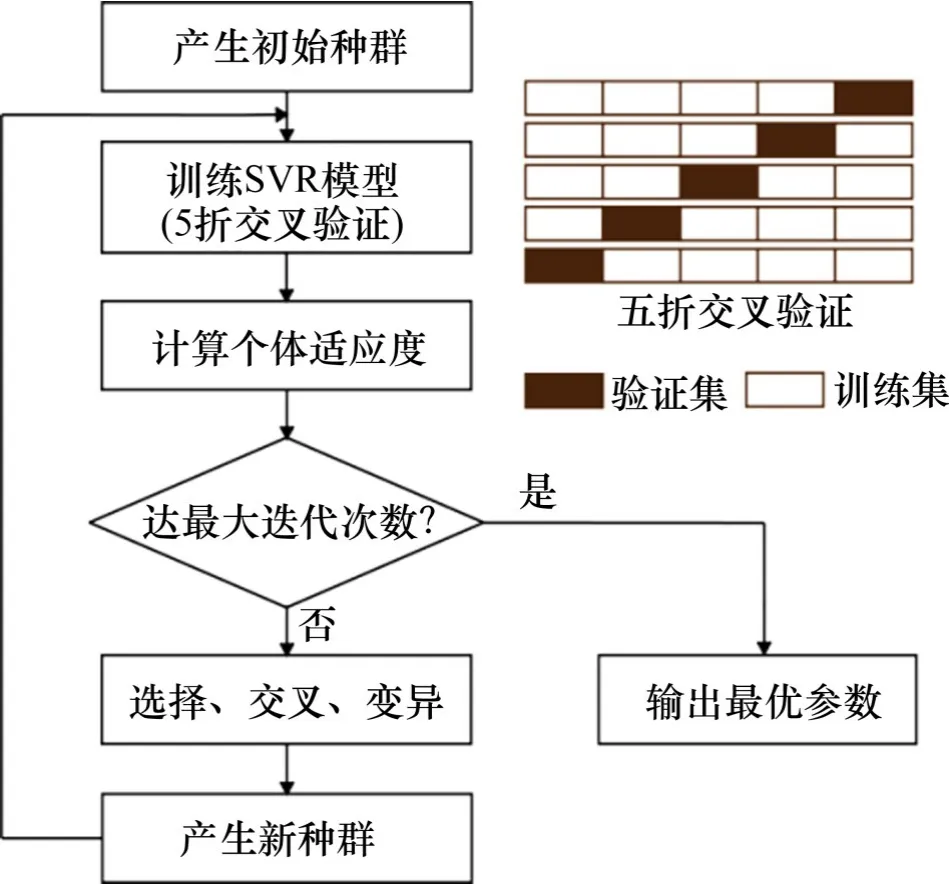
图2 参数寻优流程Fig.2 Flowchart of parameter optimization

4 案例分析

4.1 数据收集及预处理

为验证本文提出的组合预测方法在新线预测中的效果，选取某城市地铁6条线路共204组月度统计数据作为样本集。

在样本集中，输入变量包括仿真单车公里牵引能耗(X1)、仿真单车公里再生能产生量(X2)、技术速度(X3)、最小发车间隔(X4)、最大发车间隔(X5)、满载率(X6)、月均最高气温(X7)、照明设备功率(X8)以及空调设备功率(X9)，输出变量为牵引单耗(Y)。部分样本数据如表1所示。

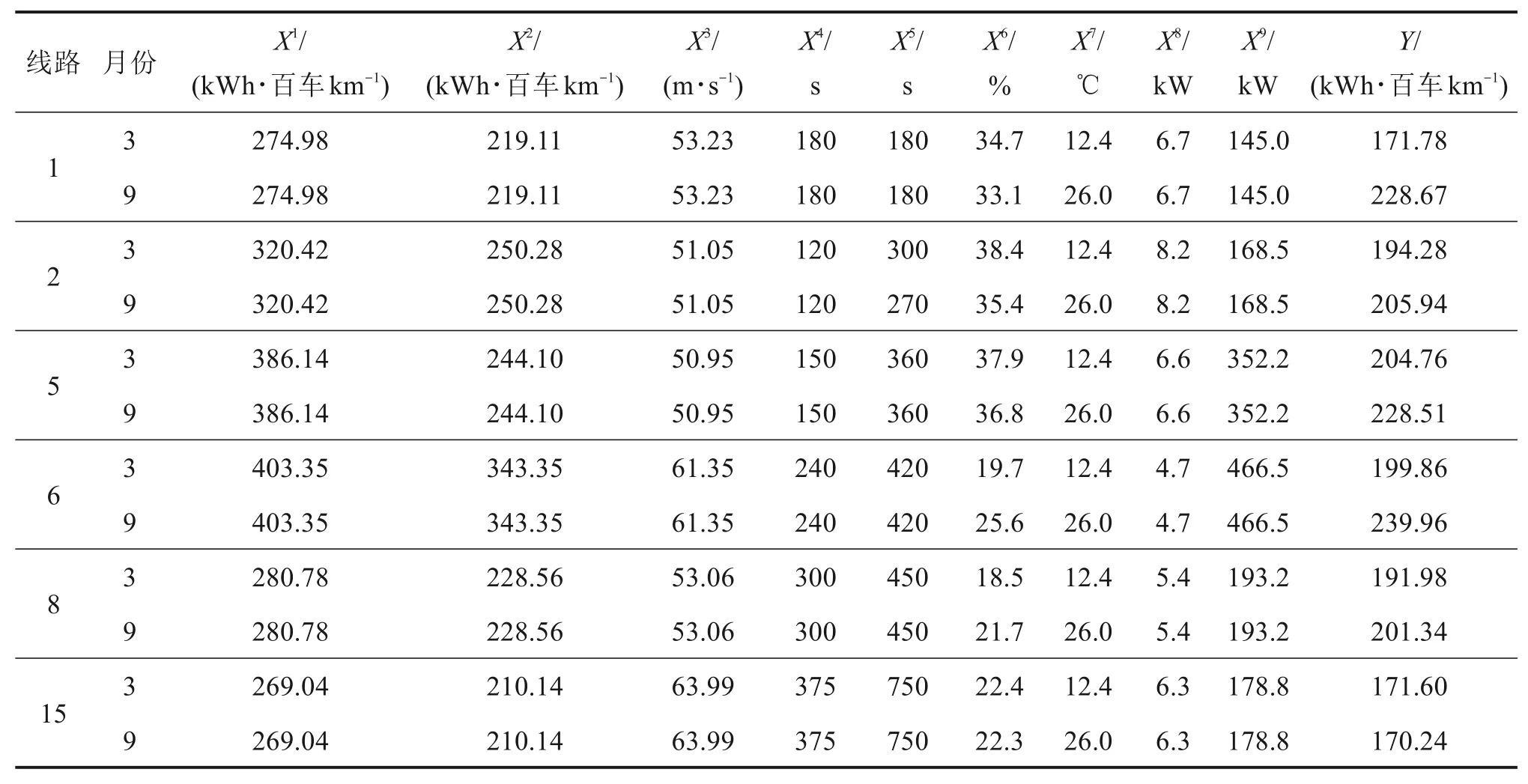
表1 样本数据Table 1 Sample data

为消除原始数据量纲影响，将输入输出变量进行归一化处理，如式(18)所示：

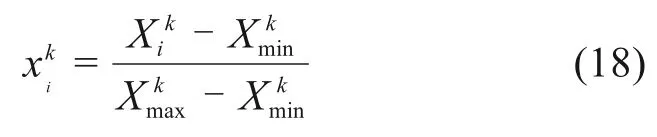
表2 预测模型MAPE及RMSETable 2 MAPE and RMSE of the predictive model

4.2 预测过程及效果

为验证本文提出方法的预测效果，假定样本集包含的6条线路中的其中1条线路作为新线，其余5条线路作为既有线路进行预测。组合预测方法通过提取既有线路中单耗影响因子与单车公里牵引能耗间的特征关系，实现新线单耗的准确预测。本文设计了2个案例来验证提出的组合预测方法在提取特征关系以及预测新线单车公里牵引能耗的使用效果。

案例1：假定2号线为新线，使用2号线所包含的60组数据做预测集。其余5条线路包括1，5，6，8，10，15号线共144组数据做训练集。

案例2：假定5号线为新线，使用5号线所包含的60组数据做预测集。其余线路包括1，2，6，8，10，15号线共144组数据做训练集。

由于遗传算法在参数选择中具有一定的随机性，本文采取重复计算10次的方法来保证预测稳定性，取10次预测结果的平均值为最终参数输出。其中，2号线及5号线的预测结果分别如图3和图4所示。

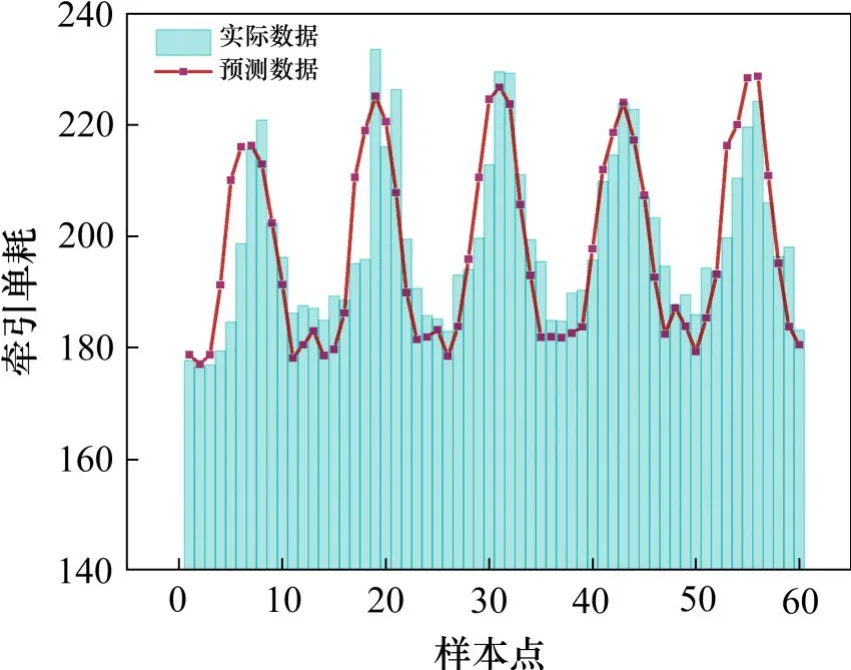
图3 2号线预测结果Fig.3 Predictive results of line 2

图3和图4结果显示，2号线和5号线预测结果与实际数据差别不大。为量化其预测效果，采用平均百分比误差(MAPE)和均方根误差(RMSE)计算预测数据与实际数据的偏差程度，其计算公式为：

图4 5号线预测结果Fig.4 Predictive results of line 5

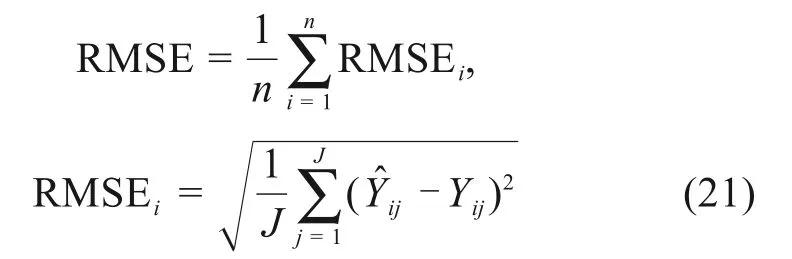
式中：代表预测牵引单耗；Yij代表实际牵引单耗。i代表样本点序号；j代表重复次数序号。

表2所示为2号线和5号线预测的MAPE值和RMSE值，结果显示，本文提出的组合预测方法在2号线和5号线单车公里牵引能耗预测中均表现出良好的效果，证明了本文组合预测方法可有效提取既有线路中影响因子与单耗的特征关系，可普遍适用于地铁新线单耗预测。

为分析遗传算法在选择SVR参数中的稳定性表现，以相对误差RE量化10次预测结果，其计算公式为：

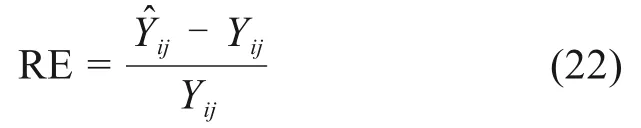
图5和图6所示结果为2号线和5号线10次预测中各样本点的相对误差。可以看出，10次重复预测中，各样本点的相对误差趋于一致，说明预测的稳定性较高。

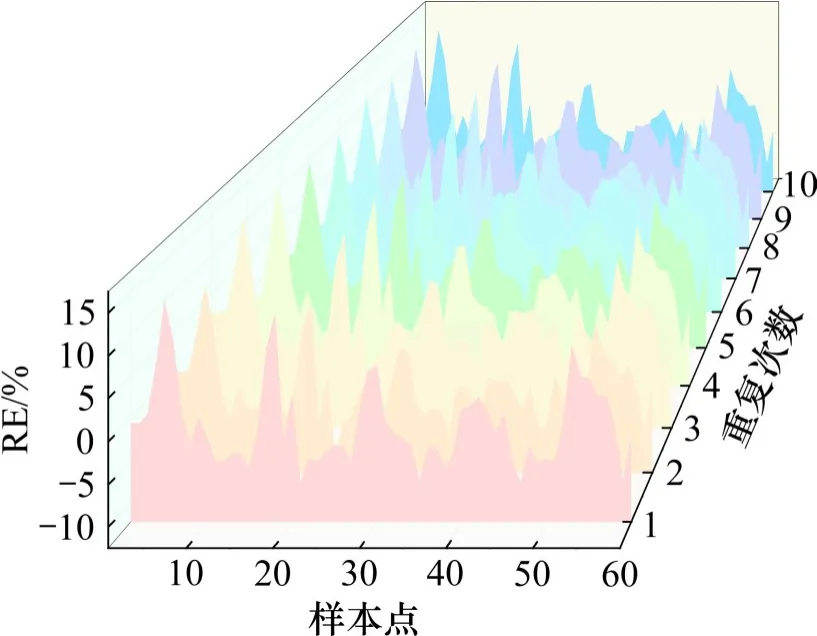
图5 2号线相对误差Fig.5 RE of line 2

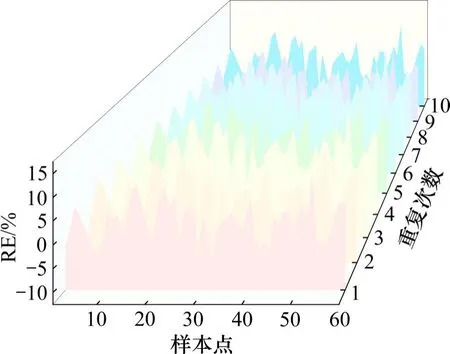
图6 5号线相对误差Fig.6 RE of line 5

同时，分析各样本点相对误差可以发现，在95%的置信水平下，2号线和5号线预测精度可达90%。

4.3 不同方法对比

为验证本文组合预测方法相比其他预测方法在地铁新线单耗预测中的适用效果，设计2组对比案例，分别采用“SVR”预测方法及“仿真+BP神经网络”预测方法。

“SVR”预测方法不采用仿真刻画线路条件及列车性能因子，仅使用SVR模型进行预测。此时，输入变量变为平均站间距、站中心位于凸面比例、坡度绝对平均值、曲线总长占全线比例、列车质量、车辆编组数量、技术速度、基本阻力、最小发车间隔、最大发车间隔、满载率、气温、照明设备功率、空调设备功率14个变量。其余参数包括样本集选取、遗传算法参数选择及重复次数等均保持不变。

表3所示预测结果表明，无仿真的“SVR”方法在2号和5号线单耗预测中的MAPE值及RMSE值均高于本文方法，说明在预测中加入仿真过程可提高新线单耗预测精度。

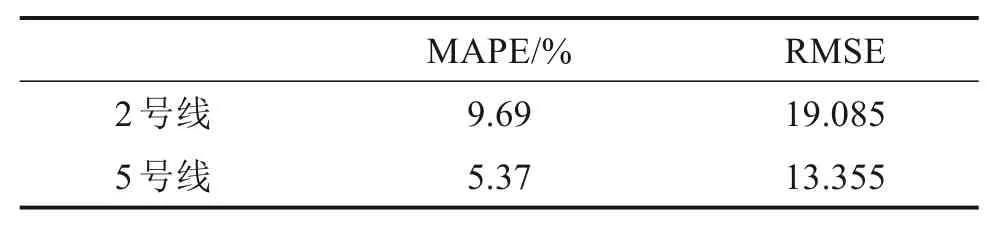
表3 “SVR”方法MAPE及RMSETable 3 MAPE and RMSE of“SVR”model

“仿真+BP神经网络”方法设计目的是为了比较“SVR”和“BP神经网络”2种机器学习方法的优劣。其预测结果如表4所示。

表4 “仿真+BP神经网络”方法MAPE及RMSETable 4 MAPE and RMSE of“Simulation+BP”model

表4所示预测结果表明，“仿真+BP神经网络”方法在2号和5号线预测中的MAPE值及RMSE值均高于本文方法，说明在地铁新线单耗预测时SVR优于神经网络。

5 结论

1)准确预测地铁新线牵引单耗对辅助新线规划设计、列车选型等有重要意义。列车牵引能耗内在机理复杂，将仿真和支持向量回归相结合进行预测，可结合列车运行仿真及大数据预测模型的双重优点，实现新线单车公里牵引能耗的精准预测。

2)案例结果表明，采用本文提出的仿真和SVR相结合的预测方法，在95%的置信水平下，地铁新线单车公里牵引能耗的预测精度可达90%。且本文方法优于传统的“SVR”预测方法和“仿真+BP神经网络”预测方法。下一步将对再生能进行更详细的刻画，进一步提高地铁新线牵引单耗的预测精度。