轨道车辆三电平储能充电多模控制策略研究
2021-11-13黄权威李蔚于越张文璐张泽刘纪龙
黄权威,李蔚,于越,张文璐,张泽,刘纪龙,2
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
与两电平直流变换器相比,三电平直流变换器开关管电压应力更小、工作效率与稳压精度更高,动态响应更快、输出调节方便,近年来在混合动力动车组、有轨电车等轨道车辆储能充电系统中广泛应用[1−3]。相较于电动汽车等其他交通工具,轨道车辆储能系统充电过程要求在车辆到站的30 s内完成[4]。充电系统如何快速高效完成充电目标是目前轨道车辆储能系统主要面临的挑战之一。充电控制策略是影响储能系统充电性能的关键因素之一[5−6]。国内外学者对充电控制策略进行了大量研究。罗成渝等[7−10]对恒流及恒压充电控制策略的理论及算法实现进行了研究。恒流充电策略具有良好的防过流特性,常作为车辆动力储能系统充电启动环节的控制策略,但恒流充电策略无法自行结束整个充电过程,实际工程应用中常与其他充电策略组合使用。恒压充电策略可以随着负载电压的变换自动调整输出电流,但充电初期输出电流过高,容易损伤车辆储能充电系统器件,降低车辆储能系统寿命。恒流恒压充电策略兼具以上两种充电方式优点,是车辆动力储能充电系统常用的控制策略,但充电时间较长,切换过程电流振荡较大[11−12]。RIVETTA等[13−16]对恒功率充电控制策略进行了系统研究,恒功率充电过程中随着负载电压的升高,输出电流逐渐降低,输出电压电流在合适区间内变化,输出功率保持不变,相较于恒流恒压充电控制策略,充电过程更加平滑,但存在充电初期输出电流过高、容易损害车辆储能系统。针对以上问题,本文对有轨电车储能充电系统的控制策略进行研究,提出一种恒流恒功率恒压多模充电控制策略,并对控制策略状态切换点的选择时机进行理论分析,通过提高恒流环节的充电电流,经过恒功率环节将充电电流逐渐降低,并利用恒压环节结束整个充电过程,集成恒流、恒功率、恒压三种单一充电策略优势,在保证系统稳定的基础上,实现电压电流全过程控制,缩短超级电容充电时长。
1 三电平直流变换器拓扑结构分析
三电平直流变换拓扑结构如图1所示。其中E为直流输入电源,输入电压表示为Uin,VT1~VT4为开关管,L为滤波电感,C1为超级电容储能装置,C2为母线电容,C3为飞跨电容,R为负载电阻。4个开关管按照VT1,VT4及VT2,VT3互补导通原则进行导通关断,保证每个开关管承压仅为输入电源的1/2,并在结构上保证飞跨电容电压趋于母线电压的一半。根据4个开关管导通关断组合规则,可以将系统工况分为以下几种模态。

图1 储能系统三电平直流变换器拓扑结构Fig.1 Three-level DC/DC converter for energy storage system
模态1:如图2(a)所示,VT1和VT2关断,VT3和VT4导通,输出端为0电平状态。输出侧由于滤波电感续流作用,负载电流通过VT3及VT4形成续流回路。输出端电压为0电平状态。
模态2:如图2(b)所示,VT1和VT3关断,VT2和VT4导通,飞跨电容电流流经VT2、滤波电感、超级电容及负载电阻经VT4回到电容负极。输出端电压为Uin/2电平状态。飞跨电容向负载侧超级电容放电,电容电压下降。
模态3:如图2(c)所示,VT3和VT4关断,VT1和VT2导通,输入电压源直接给超级电容供电,输出端电压为Uin电平状态,飞跨电容C3被旁置,无电流流入流出,输出端电压为Uin电平状态。
模态4:如图2(d)所示,VT2和VT4关断,VT1和VT3导通,输入电压源电流流经VT1,C3,VT3、滤波电感、超级电容及负载电阻回到电源负极。此时飞跨电容处于充电状态,飞跨电容电压升高,输出端电压为Uin/2电平状态。输出端电压为Uin/2电平状态。。

图2 拓扑结构不同工况下电流流向图Fig.2 Current flow diagrams under different working conditions of the three-level DC/DC converter
通过以上4种开关管开通关断模态的周期性组合使用,在保证中点电位处于动态稳定状态下,拓扑结构实现0-Uin/2-Uin的三电平模态转换。
2 主电路工况等效状态模型分析
根据上述三电平直流变换器不同工况电流流向可以得到4种开关状态下拓扑结构的电路等效模型,如图3所示。
可以根据图3所示的等效电路列写各工况下超级电容电流和电压参数变化方程:
模态1:VT1,VT2,VT3,VT4均关断时,输入电源与中点电位电压均不对负载放电,飞跨电容电压不变,负载侧输出Uout=0,如图3(a)所示。该模态的超级电容电流及电压变化情况如式(1)所示:

模态2:VT1和VT3关断、VT2和VT4导通,飞跨电容充当负载端电源,电压开始下降,负载输出Uout=Uin/2,如图3(b)所示。超级电容电流及电压在此模态下的变化情况如式(2)所示:

图3 不同工况下拓扑结构等效电路图Fig.3 Equivalent circuit diagrams of the three-level DC/DC converter under different working conditions

模态3:VT1和VT2导通,VT3和VT4关断,输入电压源充当负载电源,飞跨电容电压保持不变,输出侧Uout=Uin,如图3(c)所示。同理可得,该工况下的超级电容电流及电压方程如式(3)所示:
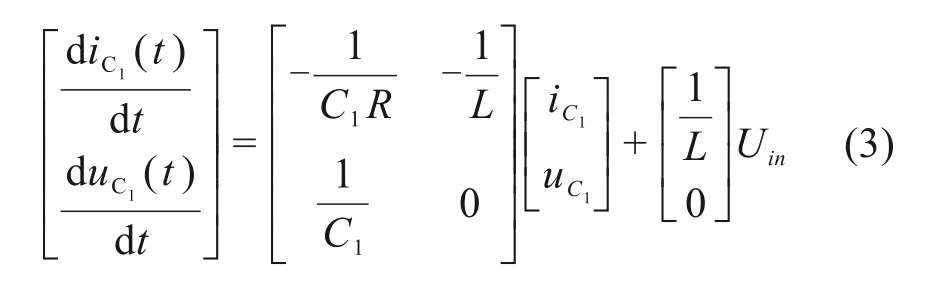
模态4:VT1和VT3导通,VT2和VT4关断,输入电压源与飞跨电容串联向负载供电,飞跨电容电压上升,输出侧Uout=Uin/2,如图3(d)所示。此工况下超级电容负载回路实质与图3(b)状态相同,其超级电容电流电压变化情况如式(4)所示:
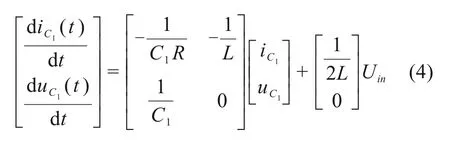
3 控制策略及其算法实现
若要通过相关控制策略实现储能系统充电目标,必须满足以下2个条件:1)为充分利用三电平直流变换器相较于两电平直流变换器的性能优势,非互补导通开关管之间应避免出现周期性同开同闭现象;2)在保证完成充电系统指定充电目标的过程中,飞跨电容电压应保持相对稳定,不能发生较大偏移。
以非互补导通开关管VT1和VT2为例,若两开关管长时间出现周期性同开同闭现象,会导致飞跨电容被旁置,模态2和模态4失效,导致三电平直流变换器退化为两电平结构,从而丧失三电平直流变换器相较于两电平变换器的性能优势。
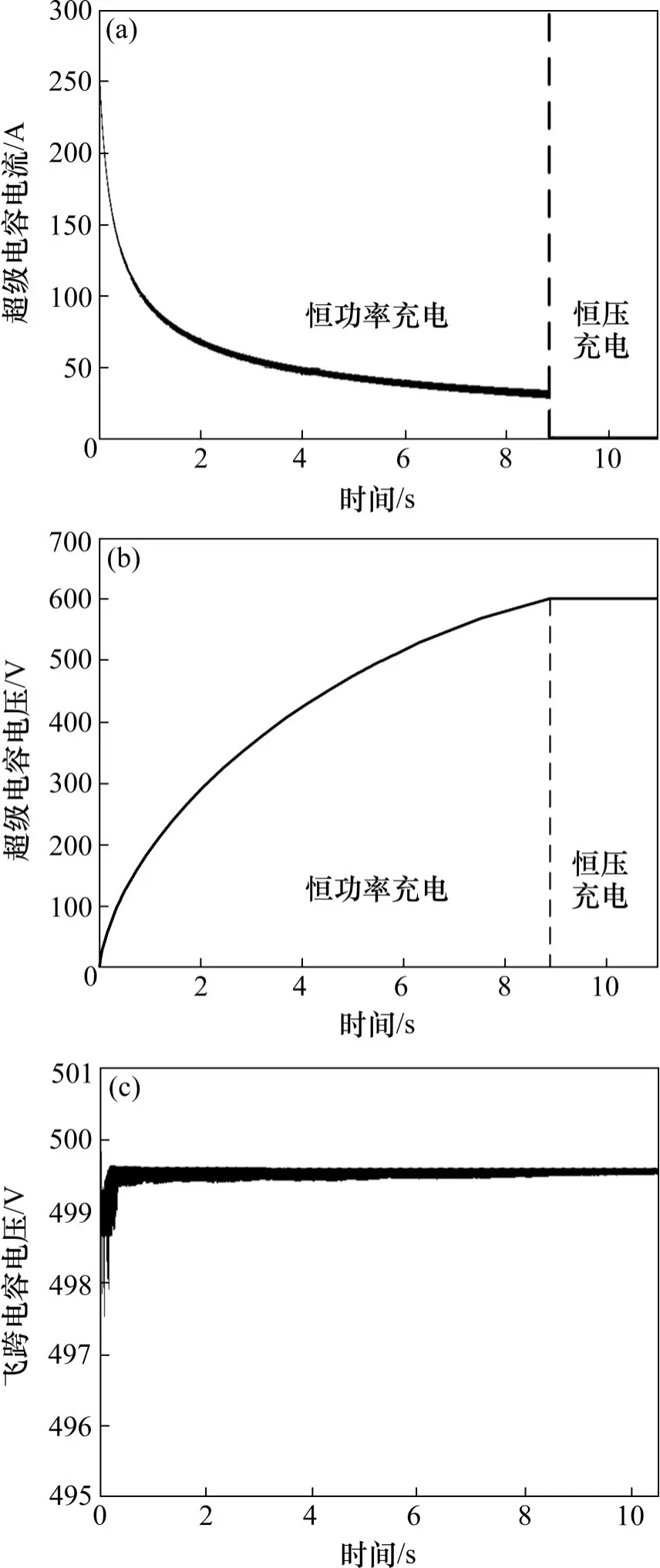
为避免此类情况发生,应将VT1和VT2之间占空比移相180°。如图4所示:由图4可以看出:0 图4 VT1和VT2导通移相180°对比分析波形图Fig.4 Comparative analysis waveform diagram of VT1 and VT2 on phase shift 180° 假设三电平直流变换器VT1和VT2导通占空比分别为D1和D2,Ts为开关周期,故单一周期内飞跨电容电压波动量及输出电压表达式为: 故当开关管VT1和VT2导通占空比相同时,中点电位电压保持稳定状态。 在工程应用中,受多种因素影响,使得两开关管之间导通时长不一致。设D1=d+Δd1,D2=d+Δd2,其中Δd1与Δd2分别表示VT1和VT2的扰动量,故扰动后的飞跨电容电压波动量及输出电压表达式为: 若保证输出电压不受多种因素扰动影响,需保证Δd1+Δd2=0,可通过施加满足上述条件的扰动量,在不影响输出电压的基础上实现中点电位自身电压波动量调整,从而实现中点电位与输出电流电压的解耦控制。 若通过控制算法实现对三电平直流变换器控制,须满足如下基本要求: 1)VT1和VT2两开关管导通占空比相同,且二者信号需延时半个周期; 2)飞跨电容进行自身电压调整,使施加于两开关管的扰动量总和为0。 为保证恒流恒功率恒压多模控制策略算法实现满足上述基本要求,将算法输出结果赋值给VT1后移相180°赋值给VT2,同时将飞跨电容电压施加于系统的扰动量正向赋值给VT1,并反向赋值给VT2。在此基础上使用PI算法实现恒流恒功率恒压多模控制策略控制目标,算法实现框图如图5所示。 图5 恒流恒功率恒压多模控制算法逻辑框图Fig.5 Logic block diagram of CC-CP-CV multi-mode control algorithm 恒流恒功率恒压多模控制策略算法以电流环为内环,功率环为中环,电压环为外环,每一环的输出值作为下一环参考值。充电过程初期超级电容电压较低,电压外环与功率中环算法输出超过限幅值,两环均以限幅值输出,电流内环以功率中环最大限幅值为参考电流,输出电流保持恒定,超级电容电压恒速率上升。当超级电容功率接近功率中环参考功率,系统进入恒功率模式,电流内环受控于功率中环。随着超级电容电压稳步上升,功率中环算法输出值逐渐降低,电流内环控制输出电流随之降低。当超级电容电压接近电压外环参考电压,电流内环、功率中环均受控于电压外环,系统切换为恒压模式。随着超级电容电压上升,电压外环算法输出值降低,系统输出电流进一步减小。当超级电容电压达到电压外环参考电压值,系统充电过程结束。 恒流恒功率恒压多模控制算法通过电流内环、功率中环、电压外环的嵌套组合,保证了控制策略的平稳过渡,实现了电压电流的全过程控制。功率中环及电压外环控制目标均通过电流内环进行实现,避免了策略硬切换过程中引起的电流震荡。 在工程应用中,由于输入电压源功率有限,储能系统充电过程存在功率界限。恒流恒压控制策略为保证系统满足要求,恒流阶段电流设定值均不超过超级电容额定输出电压时系统最大导通电流。恒流恒功率恒压控制策略在恒流控制阶段可根据器件最大导通电流确定恒流环输出电流Imax,当输出功率达到功率界限时,根据式(7)确定恒流转恒功率状态切换点A处Uref1;当超级电容电压达到额定电压时,系统充电完成,为防止系统过压控制策略切换为恒压模式,故状态切换点B处Uref2设定额定电压。由此可以保证恒流恒功率恒压多模控制策略在输出功率和器件最大导通电流限制范围内,以系统允许的最大电流输出,有效缩短充电时长。 其中:P为输入电源额定功率。 根据对主电路工况等效状态模型分析,对系统进行动态小信号模型分析,其状态空间方程可表示为: 其中:A和B为状态方程系数矩阵。对系统施加扰动,可得系统扰动方程: 将式(9)进行拉氏变换,可得系统基本状态平均方程频域表达式为: 将A,B,A1,A2,B1和B2等系数矩阵代入可得系统电流环、功率环、电压环开环传递函数GI(s),GP(s)和GU(s)分别为 通过上述对图5恒流恒功率恒压多模控制算法实现方式进行分析,可知其控制策略为三环嵌套闭环控制,算法系统控制框图如图7所示。在恒流恒功率恒压多模PI控制算法控制下的系统传递函数为: 图7 恒流恒功率恒压多模算法系统控制框图Fig.7 System control block diagram of CC-CP-CV multi-mode control algorithm 其中:DI(s),DP(s)和DU(s)为电流内环、功率中环、电压外环PI传递函数,HI(s),HP(s)和HU(s)为系统闭环反馈系数。 故系统闭环特征方程D(s)可作如下表示: 其中a,b,c,d,e,f和g为特征方程各项系数,KIp,KPp,KUp,TIi,TPi和TUi为 电 流 内 环、功 率 中环、电压外环PI参数,IL为流经电感的电流。通过上述条件约束,调整相关PI参数对系统的补偿,保证传递函数特征方程满足劳斯稳定判据,使得储能系统在恒流恒功率恒压多模控制算法中保持稳定。 根据图6中对恒流恒功率恒压多模控制策略状态切换点的选取分析,可进一步推导超级电容在恒流恒功率恒压多模控制策略下不同阶段的充电时长。 图6 控制策略状态切换点的选取Fig.6 Selection of control strategy state switching point 其中:t1,t2分别为多模控制策略中恒流、恒功率控制阶段的充电时长。 故使用恒流恒功率恒压多模控制策略下超级电容整个充电时长为 若使用恒流恒压控制策略储能系统充电目标,其超级电容整体充电时间为: 联立2种控制策略下的充电时长方程可得: 由式(26)可知:2种不同控制策略下储能系统充电快慢仅与系统输入电压,超级电容额定电压及多模控制策略恒流恒功率状态切换点有关。对式(26)进行求解可得:Uref1在0~Uout之间时,多模控制策略充电时长均短于恒流恒压控制策略。由此可以证明恒流恒功率状态切换点Uref1无论取何值,采用恒流恒功率恒压多模控制策略下的储能系统充电时长均短于恒流恒压控制策略。 为验证不同控制策略对储能充电系统工作性能的影响,搭建三电平直流变换器Simulink仿真模型及实物实验装置,分别使用恒流恒压、恒功率恒压及恒流恒功率恒压等多种控制策略对拓扑结构进行控制。有轨电车储能系统标准工况为将输入侧DC1 000~DC1 800 V电压斩波至DC950 V输出,参考有轨电车实际工况并结合实验室现有条件,实验中将DC1 000 V电压斩波至DC600 V,探究充电过程中不同控制策略下系统相关参数变化。仿真及实物实验所使用的各元器件参数如表1所示。 表1 实验参数设置Table 1 Experimental parameter setting 图8 直流变换器试验装置Fig.8 DC/DC converter test equipment 恒流恒压控制策略仿真波形如图9所示。可知:充电过程前期,系统保持恒流充电,输出电流维持在约40 A左右,随着超级电容电压匀速上升,输出电流峰值逐渐降低,波动量也逐渐增大,最大达到约5 A。在15 s时超级电容电压达到设定值,控制策略切换成恒压充电,超级电容电压保持稳定,输出电流迅速降低。在整个充电过程中飞跨电容电压保持动态稳定。 图9 恒流恒压控制策略仿真波形图Fig.9 Simulation waveform graph under CC-CV control strategy 恒功率恒压控制策略仿真波形如图10所示。可知:在恒功率充电模式下,充电过程中输出电流及超级电容电压变化较为平滑。但在超级电容电压较低时,输出电流最高可达250 A,是恒流恒压控制策略输出电流的约6.25倍,恒流恒功率恒压控制策略启动电流的约5倍。因此使用恒功率恒压充电控制策略极易超出器件最大导通电流,造成器件过流损伤甚至烧毁,不适用于对安全性要求高的轨道车辆储能系统。 图10 恒功率恒压控制策略仿真波形图Fig.10 Simulation waveform graph under CP-CV multi-mode control strategy 恒流恒功率恒压多模控制策略实验状态切换点A设置为DC400 V,状态切换点B设置为DC600 V。由图11可以看出:在恒流充电模式下输出电流保持在DC50 A左右,超级电容电压匀速上升,在8 s时达到状态切换点A,系统切换成为恒功率充电模式。在恒功率阶段,随着超级电容电压的升高输出电流逐渐减少,超级电容电压上升速率有所减缓。在13 s时,超级电容电压达到状态切换点B,系统切换为恒压充电模式,充电过程结束。飞跨电容电压在整个充电过程中保持稳定,超级电容电压在预定值附近波动。与恒流恒压控制策略相比,恒流恒功率恒压控制策略将储能系统充电时长缩短约13%。 图11 恒流恒功率恒压多模控制策略仿真波形图Fig.11 Simulation waveform graph under CC-CP-CV multi-mode control strategy 恒流恒压策略、恒流恒功率恒压策略关键节点波形图如图12所示。可知:恒流恒功率恒压多模控制算法满足了控制策略实现要求。在不同控制策略充电过程中,三电平直流变换器飞跨电容电压均在Uin/2小范围波动。实物实验波形符合仿真实验预期,验证了本文所提的控制策略的有效性。通过多个控制策略的理论分析、仿真及实物实验,充分证明了在满足储能系统安全稳定运行的前提下,恒流恒功率恒压控制策略可有效缩短超级电容充电时长。 图12 实物实验关键节点波形图Fig.12 Waveform of key nodes in physical experiment 1)本文将恒流恒功率恒压多模控制策略引入轨道车辆储能充电系统中,该策略集成恒流、恒功率、恒压单一充电控制策略性能优势,依次通过电流内环实现大电流稳定输出、功率中环实现大电流平滑过渡到较低水平,电压外环实现充电过程的平稳结束。利用三环嵌套算法,实现了3种模态的自动平稳切换及电压电流的全过程控制。 2)3种策略的仿真及实物实验表明:采用恒流恒功率恒压多模控制策略与恒流恒压、恒功率恒压控制策略相比,在输入功率和输出电流的约束范围内,实现了最大电流及最大功率输出,有效缩短了约13%充电时长。证明了在保证系统稳定性和安全性的前提下,相较于恒流恒压、恒功率恒压控制策略,恒流恒功率恒压控制策略可有效缩短超级电容充电时长,为轨道车辆储能系统在工程应用上的控制策略选择及算法实现提供了借鉴价值。



4 控制性能分析
4.1 算法稳定性分析


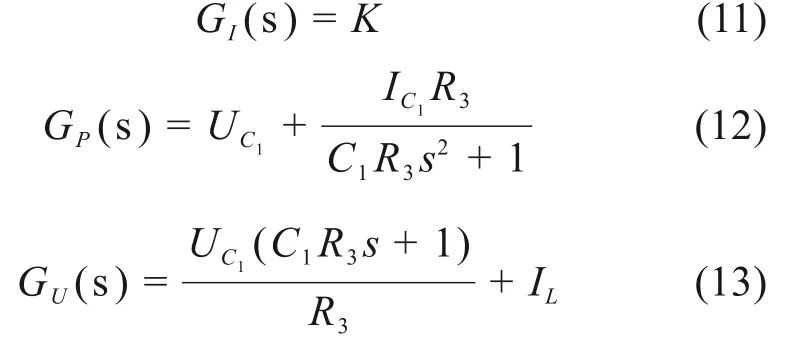


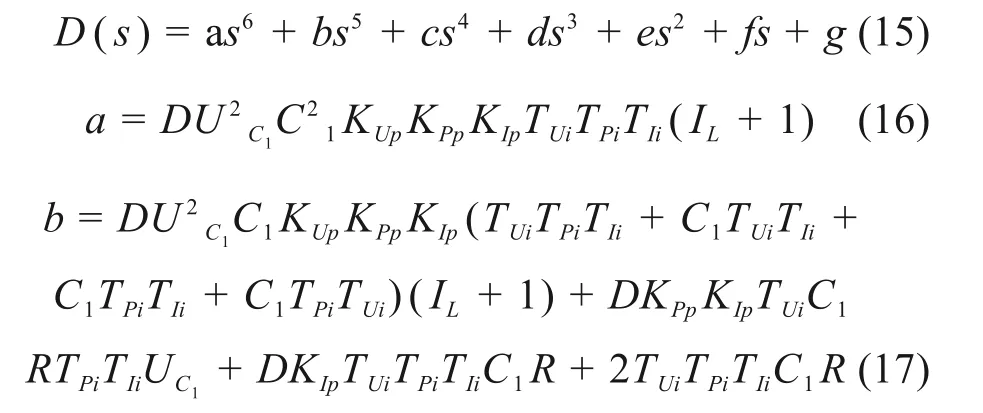

4.2 充电时长分析





5 实验验证





6 结论
