基于单元模态应变能与区间分析的不确定性损伤识别
2021-11-13鲁四平张会峰黄方林
鲁四平,张会峰,黄方林
(中南大学 土木工程学院,湖南 长沙 410075)
土木工程结构在服役期间,由于长期的荷载作用、疲劳效应、环境腐蚀、突发效应等因素的影响,内部结构必然会出现一定程度的损伤。当损伤累计达到一定程度时,可能会造成不可逆转的影响。为此,对既有结构进行健康监测具有重要的工程应用价值。损伤识别是结构健康监测的重要组成部分,已取得一定的成果,在固有频率、振型、单元模态应变能等基础上,提出静动力指纹识别方法。为精确地反映结构的真实物理特性,提出基于模型修正的损伤识别方法。仅通过所检测的结构响应来分析结构参数的变化,提出基于实测时域信号的识别方法,以及通过与大数据下的神经网络技术相结合,提出基于神经网络的结构损伤识别等方法[1]。其中基于模态应变能的损伤识别方法由于其广泛的适应性和有效性,已成为结构损伤领域的一个重要研究方向。STUBBS等[2−3]首先把模态应变能方法用于损伤破坏的诊断。随后其对损伤指标进行改进并在简支钢桥上进行准确的损伤定位。SHI等[4]提出利用单元模态变化率对结构进行损伤识别,并在2层平面钢架上进行了实验,验证了所提方法的准确性。刘晖等[5]将材料领域的耗散率引入到单元模态应变能理论中,提出一种新的损伤识别方法。颜王吉等[6]利用单元模态应变能和泰勒公式,导出了单元模态应变能1阶与2阶灵敏度损伤识别方法。YANG等[7]结合跨模型模态应变能和同步优化的优点,提出了一种2阶段损伤识别方法,基于模态应变能建立损伤指标,然后针对传统灵敏度分析计算量大的问题,引入同步优化的方法进行损伤识别。HOSSEINI等[8]对基于模态应变能的损伤识别方法进行研究,定义一种新的损伤识别影响因子,最后对所得的结果进行评价,为每一个基于该影响因子的数值算例引入最佳目标函数。现有方法大多没有考虑诸多不确定性因素的影响,如测量误差、结构体系的复杂性、环境噪声等[9],这些因素可能导致损伤识别精度下降,甚至出现误判。如何有效地解决测试中不确定性因素的影响[10]成为损伤识别中迫切需要解决的问题之一。目前,现有的不确定性分析技术方法有概率计算法、模糊计算法和区间分析方法。前2种方法都需要大量的实验数据进行计算才能确定参数所服从的概率密度函数和隶属度函数,在实际应用上具有一定的限制。区间分析方法[11]则很好地解决了测量数据较少、结构状态特征量界限难以量化的问题。王晓军等[12]较早提出将区间分析方法应用于结构损伤识别中。骆勇鹏等[13]提出了一种适用于当概率分布未知和数据样本较少时的不确定性损伤识别方法,并通过数值模拟算例和实测斜拉桥验证了方法的可行性和有效性。方圣恩等[14]在模态区间分析理论中,引入改进解析冗余度,提出一种崭新的损伤识别方法,解决了经典区间算法出现的区间扩张问题。本文首先基于多次重复测量数据,提出采用区间数来量化响应的不确定性,结合单元模态应变能理论,建立区间损伤识别方程组;然后,引入快速非支配排序遗传算法(NSGA-Ⅱ)求解该方程组,计算单元刚度折减系数区间范围,采用区间重叠度与区间中值距离构造损伤定位和损伤定量指标进行损伤识别;最后,采用数值模拟验证所提方法的有效性和可行性。
1 基于单元模态应变能理论和区间分析的不确定性损伤识别
1.1 基于单元模态应变能的结构损伤识别理论
单元模态应变能只与单元的刚度和单元对应的振型向量有关。单元模态应变能[6]为:
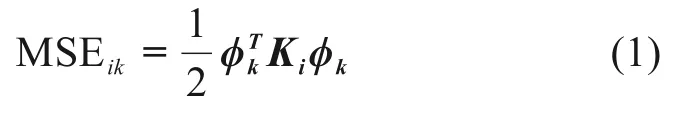
其中:φk表示第k阶振型向量;Ki是单元矩阵在整体坐标系下扩阶而来的。
以单元模态应变能的改变作为损伤识别的基本特征,依据单元模态应变能理论,将单元刚度的折减来作为损伤指标,文献[6]已经对其进行了理论推导,得出结构的损伤识别方程组为:[A]{α}={ΔS},即:

式中,损伤后的结构状态特征量用上标加d表示。下标n表示结构被分为n个单元。αi为第i单元的刚度折减系数;φdk为单元损伤后的第K阶振型;λk为结构损伤前后的第k阶特征值;Ki是单元矩阵K e i在整体坐标系下扩阶而来的;M为整体刚度矩阵。通过求解矩阵中的αi即可确定单元的损伤定位和损伤定量。
1.2 区间分析理论
区间分析可大致分为区间算数运算法,区间截断法,区间组合法[15]和区间优化算法[16]。但无论是区间算数方法还是区间组合方法都要求响应量随着变量在区间内单调变化,或者要求变量之间相互独立。但是,在仿真或者实验中很难看出响应量在变量区间中的规律变化,单纯的利用区间算数或者区间组合就会导致区间出现扩张,难以满足实际要求。
区间优化算法能较好地解决上述出现的问题。NSGA-Ⅱ遗传算法是一种快速非支配多目标优化算法。求解区间范围的流程如下:1)在变量区间内随机生成一个由多个个体组成的初始种群P0,以函数minf(a)作为目标函数,采用NSGA-Ⅱ遗传算法对minf(a)进行优化求解,将得到目标函数值的最优解αi作为下限值。2)同理以种群P1为初始种群,采用NSGA-Ⅱ遗传算法求解响应量αi的上限值,因此也就得到了响应量c的取值范围。即在区间的变化范围内求区间的上下限。
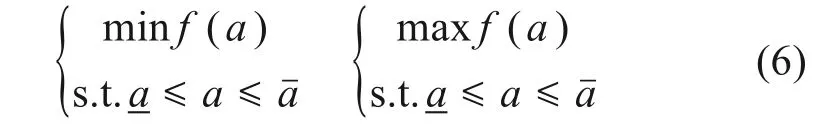
式中:minf(a),maxf(a)为优化函数的目标函数。
利用NSGA-Ⅱ遗传算法求解上述2个优化方程,所得到的最大化和最小化函数的解即为响应量αi的区间范围。
2 不确定性损伤识别的区间算法流程
2.1 损伤指标不确定性量化
因为在实际工程测量中,结构的响应往往会受到很多不确定性因素的影响,并且往往结构在实际的实验过程中无法测得足够多的实验数据,用来确定参数服从的概率密度函数。而区间分析理论则只需很少的实测数据即可对其进行损伤识别。因此损伤识别步骤为:
1)多次重复测试数据,求出系数矩阵、系数向量中各个元素的取值区间。系数矩阵及系数向量也就变成区间矩阵。
2)损伤识别方程也变成损伤区间识别方程组。
3)在此基础上,采用NSGA-Ⅱ区间优化算法求解损伤区间方程组,并转化成为对区间向量中各元素上下界的优化问题。
假设αi为第i个单元刚度损伤指标,则它的最小值和最大值将转化为:

单元刚度损伤矩阵αi的求解也就转变成已知变量取值范围下,αi求解最大值最小值的问题。多次重复上述操作即可得到单元刚度损伤指标α的区间向量:
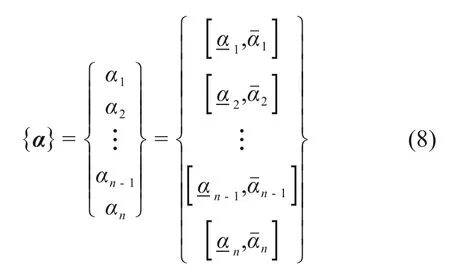
2.2 基于区间分析的损伤指标构建
对相关结构进行测试,获得相关测试数据后,采用前述损伤识别步骤可得出损伤识别指标αi的损伤区间,,由于通过区间的相互分离来判定结构是否发生损伤显得不够直观和明显,因此定义区间重叠度[17]来进行识别:
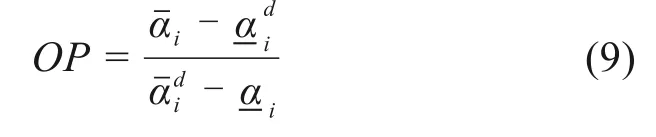
通过计算OP指标的所有情况如下:
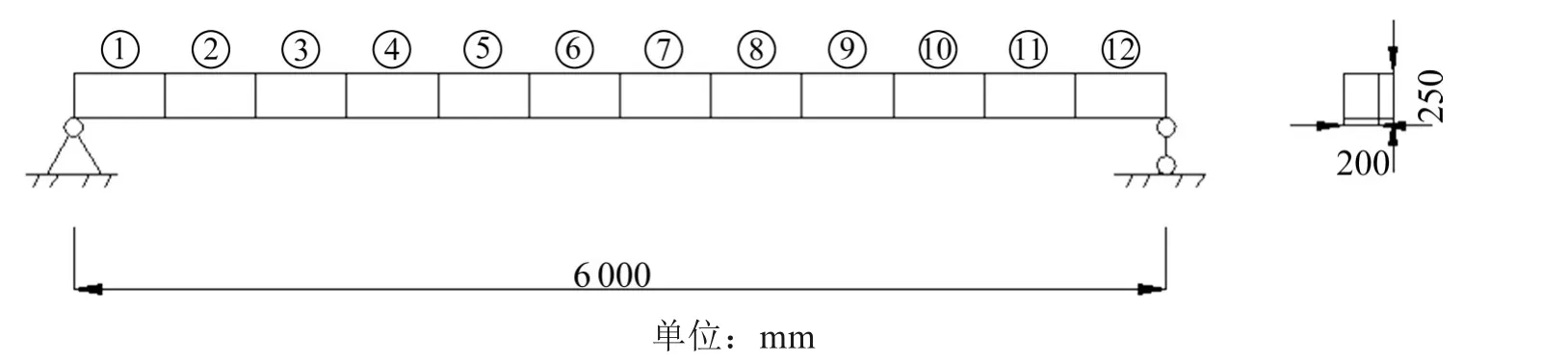
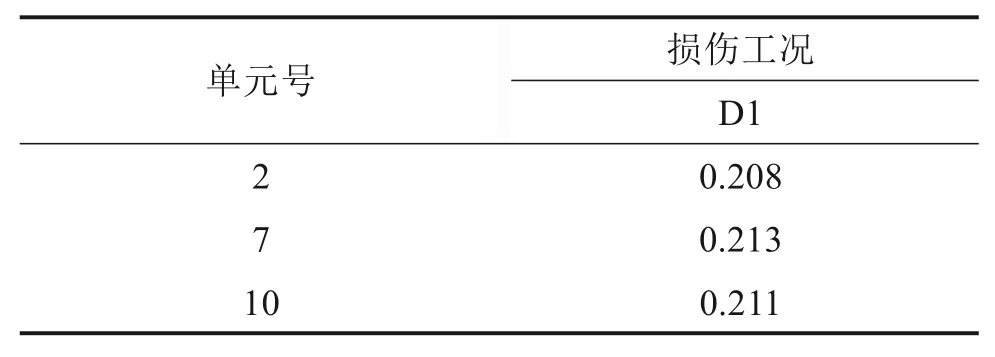
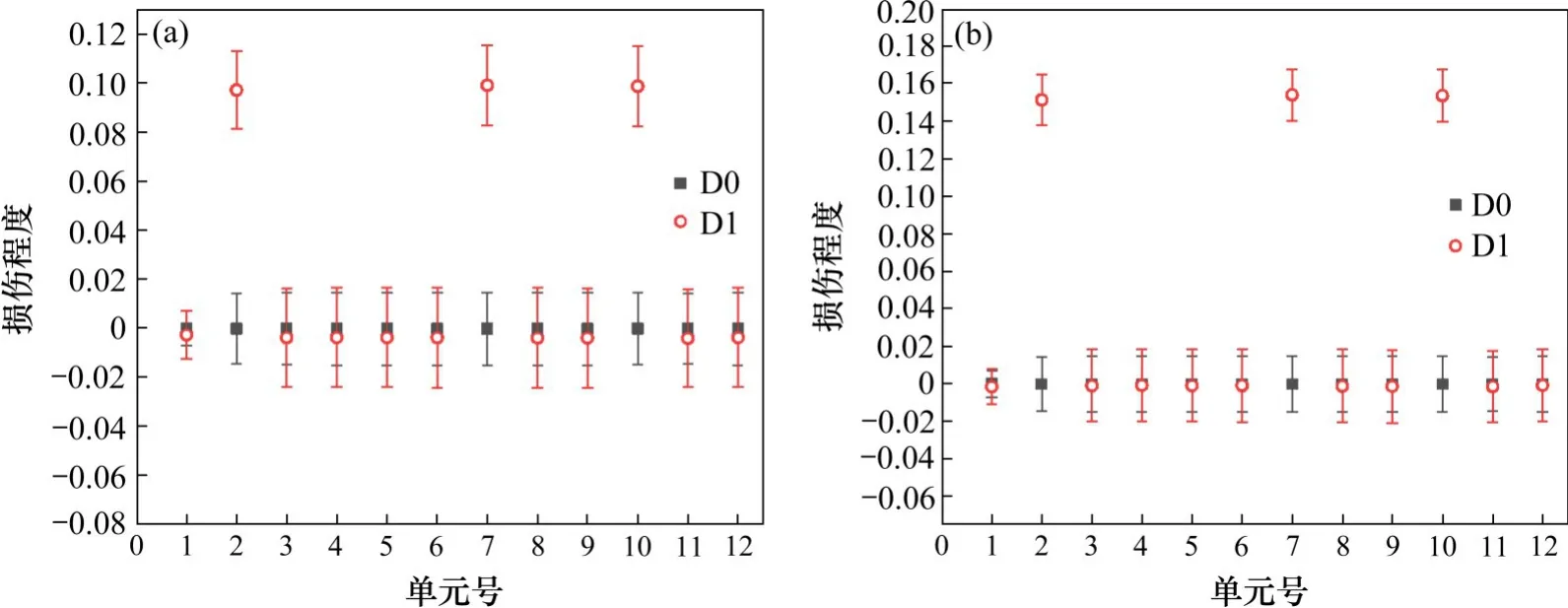
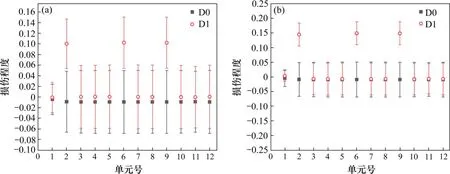
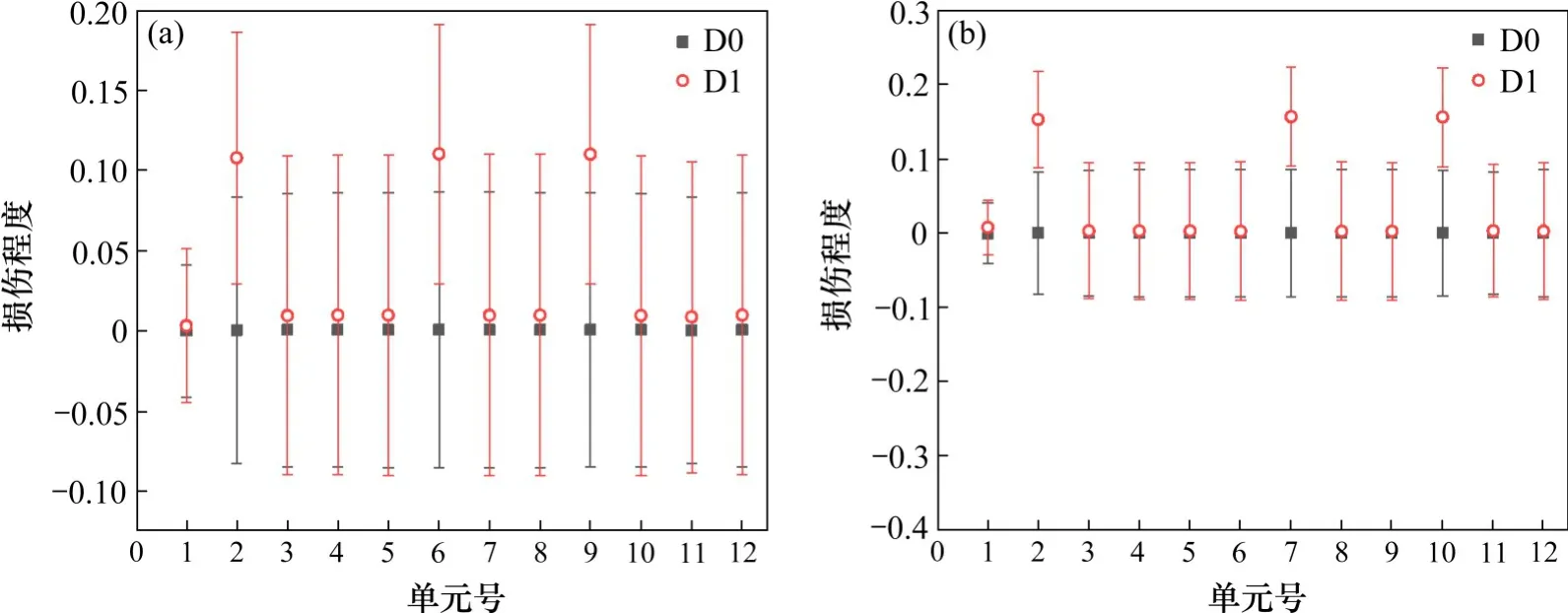
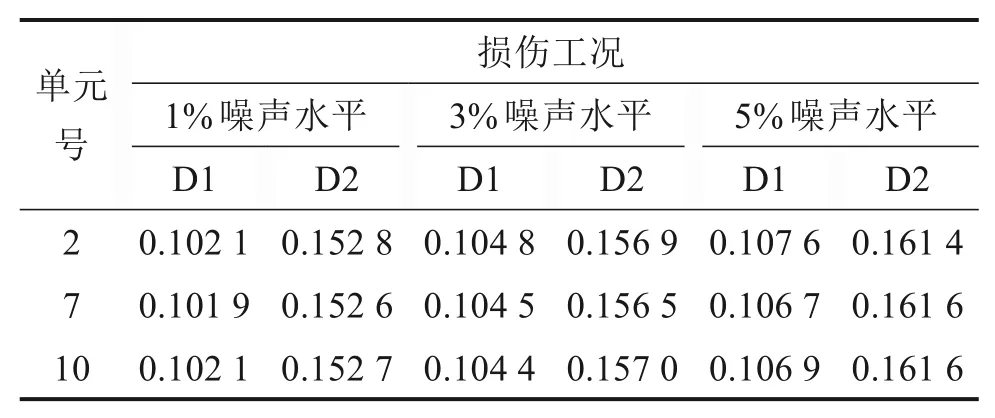
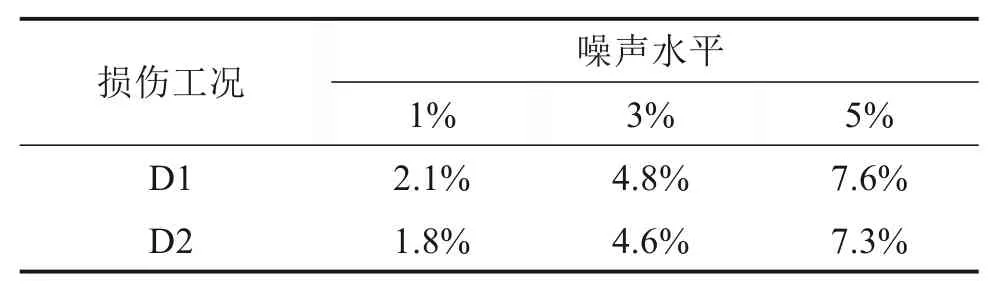
由图1可以看出,OP=1,以及OP≈1时可以判定结构未发生损伤;OP≤0,判定结构严格发生损伤;当0 图1 区间重叠度示意图Fig.1 Overlapping rate 当αi和的中值分别与的下限和αi的上限重合时,OP=1/3,故选取1/3作为判断结构是否损伤的阈值。当OP<1/3时,定义为损伤;反之,OP>1/3时,结构未损伤。 定义区间中值的差值IM作为损伤程度的定量标准, 简支梁长6 m,梁截面为0.2×0.25 m2,弹性模量E=32 GPa,密度ρ=2 500 kg/m3,梁被划分成12个单元,单元均长为0.5 m。采用降低单元刚度的方式来模拟结构单元损伤,共设计3个损伤工况,不同工况对应不同损伤位置及单元损伤程度,见表1。 表1 损伤工况Table 1 Damage cases 在实际工程测量中,结构的响应往往会受到测试噪声的影响,考虑观测数据不确定性的影响是很有必要的。测量噪声采用均值为0,方差为1高斯白噪声模拟,并将其直接加入到测量的振型和频率中去,因此加入噪声后的频率和噪声分别为: 式中:wk与分别为受噪声污染前后的第k阶特征值;φki与分别为受噪声污染前后的第k阶第i单元的振型;rw,rφ分别为特征值与振型的噪声水平;频率噪声、振型噪声为1%,3%,5%,用来考虑模型误差和测量误差;ρ为随机变量,服从于均值为0,标准差为1的正态分布。由于在实际的测量过程中往往无法测得足够多的数据,本文采用重复多次(50次)的方法,模拟来求的结构状态特征量的取值区间。 按照区间分析的损伤指标不确定性量化识别步骤进行计算各损伤工况下的αi的取值区间以及OP取值表见图3~5与表2。由图2和图3可知在噪声水平为1%和3%情况下,损伤单元在损伤状态下与健康状态下的区间完全分开,严格判定结构损伤,并没出现误判与漏判的情况;当噪声水平为5%时,损伤单元取值区间出现重合,故采用OP指标进行判定。根据表2可得出,区间重叠度指标值均小于1/3,判定结构出现损伤,损伤识别未出现误判和漏判。 图2 简支梁的模型Fig.2 Simply beam model drawing 表2 5%噪声水平下D1损伤工况下的OP指标Table 2 OP index under D1 damage condition under 5%noise level 图3 噪声水平为1%时,健康状态和损伤状态下的αi区间范围Fig.3 Range ofαi values for healthy and damaged states at 1%noise level 图4 噪声水平为3%时,健康状态和损伤状态下的αi区间范围Fig.4 Range ofαi values for healthy and damaged states at 3%noise level 图5 噪声水平为5%时,健康状态与损伤状态下的αi区间范围Fig.5 Range ofαivalues for healthy and damaged states at 5%noise level 其次采用IM指标进行损伤程度识别,结果如表3所示。为了进一步描述识别效果的好坏,定义损伤程度相对识别误差值: 式中:̂是采用本文方法所测得的结果;αi是真实的损伤值;|·|是结果的绝对值。 由表3~4可知: 表3 各噪声水平下各损伤工况的IM指标Table 3 IM index of each damage condition under various noise levels 1)对于任何损伤工况,本方法均能准确对单元进行损伤定位,未出现误判和漏判; 2)随着噪声水平的增大,损伤程度的识别精度有所降低,在5%噪声水平工况下,损伤单元损伤程度最大识别误差为7.6%。 表4 最大相对识别误差Table 4 Maximum relative recognition error 1)土木工程结构常常受到各种不确定性因素的影响,原有模态应变能理论以确定性分析方法为主,提出一种基于单元模态应变能理论与区间分析理论相结合的不确定性损伤识别方法,通过区间重叠度与区间中值距离构造损伤定位和损伤定量指标,识别损伤的目的。 2)数值算例表明,在不确定性因素的影响下,该方法能对损伤单元进行准确定位,其损伤程度的定量识别精度随着噪声水平的增大而有所降低,当噪声水平取5%时,损伤最大相对识别误差值为7.6%。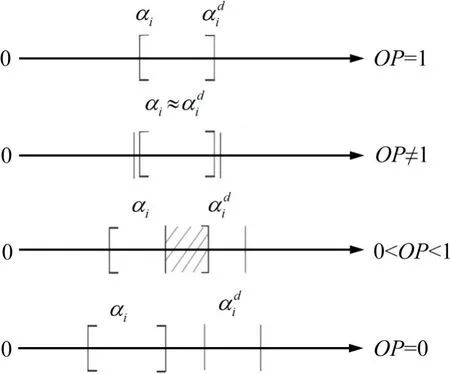
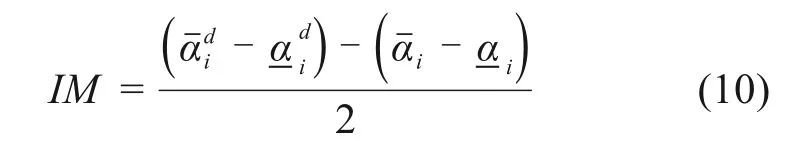
3 数值模拟验证

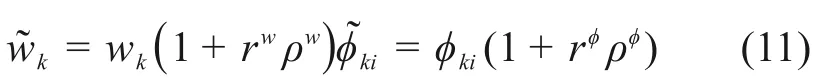
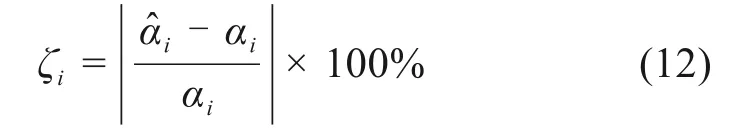
4 结论
