基于高职物流管理专业的数学建模应用案例研究

■王雪

（武汉交通职业学院公共教学与实践学院，湖北 武汉 430065）

高职物流管理专业的培养目标是为适应社会主义市场经济需要，为物流企业培养具有一定的物流管理和物流信息处理能力，能在物流领域从事采购、供应、运输、调度、仓储、配送、销售等物流核心环节的实务运作工作的高素质技能技术物流人才。数学建模是物流管理专业开设的重要基础课程，教学内容包括线性规划、图论、贮存等经典数学模型，这些数学模型在物流领域广泛应用，能为物流企业依据效益最大化原则进行资源优化配置提供科学依据，提升企业核心竞争力。但数学建模教学中还存在如下问题:教学内容陈旧，与物流专业问题联系不够紧密；模型求解注重数学理论和数学计算；鲜有运用快捷方便的数学软件求解等问题。这些问题导致学生不能灵活应用所学建模知识解决专业问题，严重影响了学生的核心职业能力和创新能力培养。因此，很有必要探讨数学建模在物流管理中的应用案例，使数学建模教学更好地为专业教学服务。

一、数学建模在优化采购方案中的应用

采购是一项保证物流企业正常开展生产及经营活动的重要物流活动，一方面为企业获取生产资源，为企业带来效益；另一方面采购过程中，也会产生采购成本[1]。采购时要努力追求科学采购，就是以最少的成本去获取最大的效益，追求利润最大化。因此，制定科学合理的采购方案是实现企业经济利润最大化的基本源泉，有助于提高企业竞争力。下面通过案例，阐述如何利用数学模型制定科学合理的采购方案。

案例1:某企业生产三种不同产品，需要同一种资源，采购主管从两个资源产地G1、G2进行采购，两个产地的产量分别为48吨、56吨，三种产品分别在三个分厂C1、C2、C3生产加工，根据生产计划安排，三种产品分别各需要这种材料37吨、22吨、32吨。从G1产地采购单位材料能给三个分厂带来的利润分别为6、3、8；从G2产地采购单位材料能给三个分厂带来的利润分别为5、9、7，其中利润单位为（百元/吨）。请问采购主管制定怎样的采购计划，才能使企业获得最大利润。

分析问题:由案例知两个产地的总产量为104吨，大于三个分厂的总需求量91吨，属于供大于求的采购模型。由此可知采购方案有很多种，但采购时要满足条件:每个产地的总采购量不能超过该产地的产量；每个分厂采购的原材料质量要等于该分厂的需求量。现从众多采购方案中选择获得最大利润的方案，这个问题可以转化为目标函数最大化的线性规划模型。现建立模型如下:

设Cj分厂从Gi产地采购xij单位的原材料，i=1,2，j=1,2,3，则目标函数为:

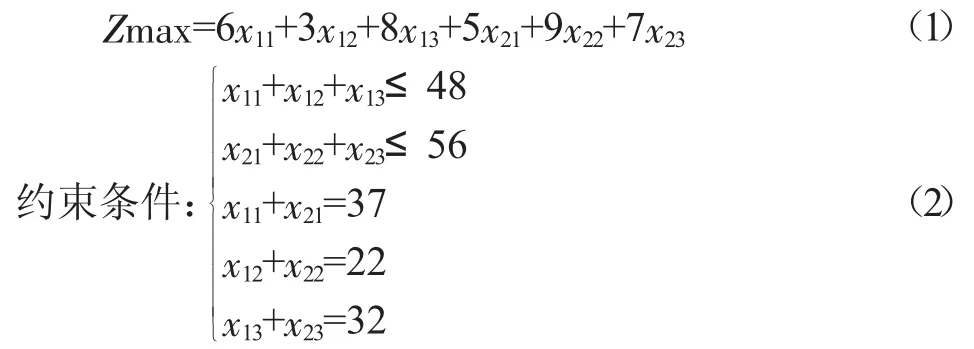
模型求解:现有数学建模教材中介绍的是单纯形法求解[2]，但是单纯形法计算步骤复杂、计算量大、学生不易掌握，不利于培养学生学习兴趣及解决问题的能力，下面介绍简单、快速、准确的LINGO软件求解步骤，并给出结果分析。

首先打开LINGO软件窗口，在窗口中输入上面建立的线性规划模型，注意，每个语句之间用英文状态下的分号隔开[3]，如图1所示。

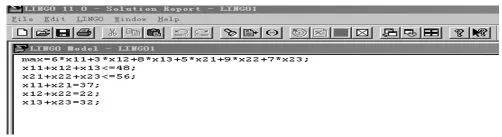
图1 线性规划模型输入

然后点击工具栏上的求解按钮，1秒钟即可得出模型求解结果，如图2所示。

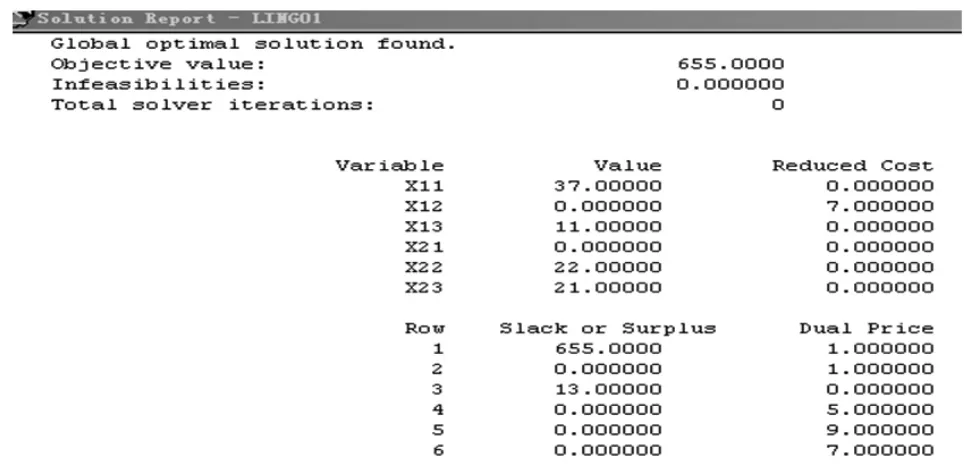
图2 模型求解结果

最后对模型结果进行分析，由图2可得出:x11=37，x13=11，x22=22，x23=21，Objective value为 655。结合前面假设知，最优采购方案为:C1分厂所需的37吨全部从G1产地采购，C2分厂所需22吨全部从G2产地采购，C3分厂所需11吨从G1产地采购，另外21吨从G2产地采购，企业获得最大利润为65500元。

二、数学建模在优化调运方案中的应用

运输是物流系统的核心，运输费用在物流各环节费用中占比重较大，因此合理优化运输方案，降低运输费用对降低物流系统成本起着至关重要的作用。

案例2:某物流企业从三个仓库调运某批货物到四个需求地，三个仓库分别为W1、W2、W3，它们的最大储存量分别为55吨、43吨、52吨；四个需求地分别为K1、K2、K3、K4，四个需求地的需求量分别为:35吨、45吨、40吨、30吨；从仓库 W1调运货物到 K1、K2、K3、K4四个需求地的单位货物运价分别为9百元/吨、8百元/吨、7百元/吨、2百元/吨；从W2调运货物到K1、K2、K3、K4四个需求地的运价分别为3百元/吨、9百元/吨、3百元/吨、1百元/吨；从W3调运货物到K1、K2、K3、K4四个需求地的单位运价分别为5百元/吨、6百元/吨、4百元/吨、3百元/吨；请问物流企业制定怎样的调运方案，使物流企业运费最少。

解决这一问题，传统数学建模课程中采用的是表上作业法[4]，表上作业法同样存在计算量大、结果容易出错等缺点，多数高职学生不能很好地把表上作业法应用到实际工作中。下面探讨通过建立数学模型，利用LINGO软件求解。

分析:从案例知，三个仓库的总储存量等于四个需求地的总需求量，这是供需平衡的运输问题，存在多种调运方案。但是调运时要满足每个仓库运往需求地的货物运量不得超过仓库的最大储存量，三个仓库运往同一个需求地的货物总量不得小于需求地的需求量。现从满足条件的众多方案中选择运费最少的方案。假设从第i个仓库Wi运往第j个需求地Kj的货物为xij吨。cij表示从仓库Wi运往需求地Kj的货物的单位运价，ai表示仓库Wi的供应量，bj表示需求地Kj的需求量。

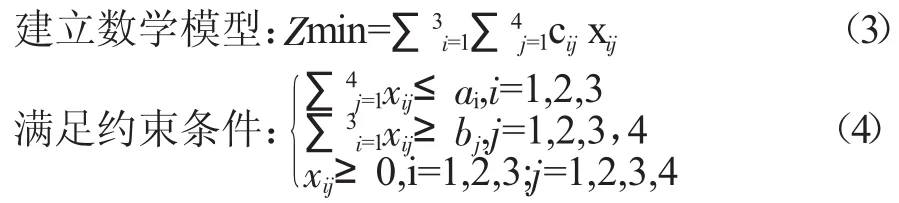
说明:模型中式（3）表示求运输费用函数的最小值；式（4）中第一个表达式表示三个仓库各自运往四个需求地的总运量应不超过各自的最大储存量55吨、43吨和52吨；式（4）中第二个表达式表示三个仓库运往四个需求地的总运量应不小于四个需求地各自的需求量35吨、45吨、40吨和30吨。

通过lingo软件求解模型，制定出最优的运输方案为:W1调运25吨货物到K2，调运30吨货物到K4；W2调运35吨货物到K1，调运8吨货物到K3；W3调运20吨货物到K2，调运32吨货物到K3，最少运费为63700元。

三、数学建模在优化仓库租用合同签订方案中的应用

案例3:某物流公司在2021年的1—3月的3个月内拟租用仓库。已知各月份所需仓库面积分别为:1500、1000、2500平方米。仓库租借费用随租用期限而定，租用1个月的费用为30元/平方米；租用2个月的费用为50元/平方米；租用3个月的费用为60元/平方米。租借仓库的合同每个月初都可办理，合同内容规定租用面积和期限，每次可以同时签订多份合同。请为该公司签订租借合同的最优决策，使租借费用最小。

分析:分析案例知租用方案有多种，租借时只需满足如下条件:各份合同中1月份的租用面积之和等于1500平方米，2月份的租用面积之和等于1000平方米，3月份的租用面积之和等于2500平方米。现制定使租借费用最小的租用方案。为便于把上述问题转化为数学问题，假设xij为第i个月月初开始租借且租借期限为j个月的租用面积。因为只有1—3个月需要租用仓库，如果第2个月初开始租借，租借期限最长为两个月，如果第3个月月初开始租借，租借期最长为1个月，故x23=x32=x33=0

利用lingo软件求解模型，可得出x11=5,x31=15,x13=10，x21=x12=x22=0。因此，最优的合同签订方案为:1月初签订1份租期为1个月、租用面积为500平方米的合同，再签订1份租期为3个月、租用面积为1000平方米的合同；3月初签订1份租期为1个月、租用面积为1500平方米的合同，最小的租用费用为120000元。

四、数学建模在销售人员任务分派中的应用

案例4:某企业销售部门拟派4名销售业务员制作4种不同产品的营销方案，每名业务员负责一种产品的营销方案制作。按照4名业务员上报的营销方案，完成销售工作预计为企业带来的利润（单位:百万元）见表1，请为4名业务员分配工作任务，使企业利润最大。

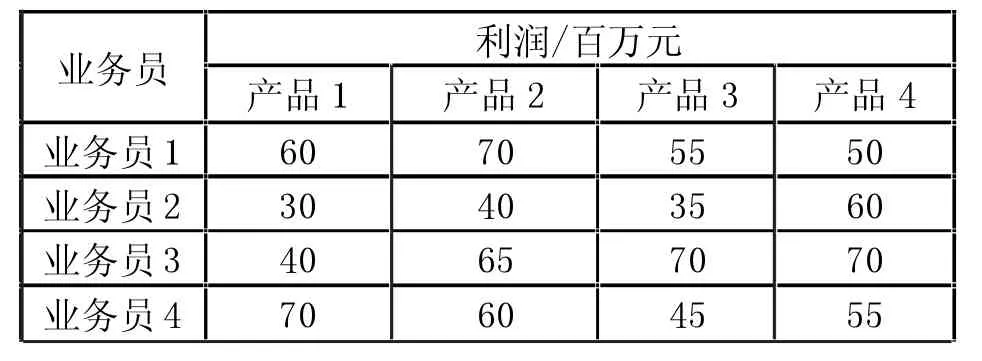
表1 预计利润

分析:这属于典型的指派问题[5]。设cij表示业务员i负责产品j的营销方案为企业带来的利润。设0-1决策变量为xij，xij=1时，表示业务员i负责产品j的营销方案，xij=0时，表示业务员i不负责产品j的营销方案。

建立数学模型:

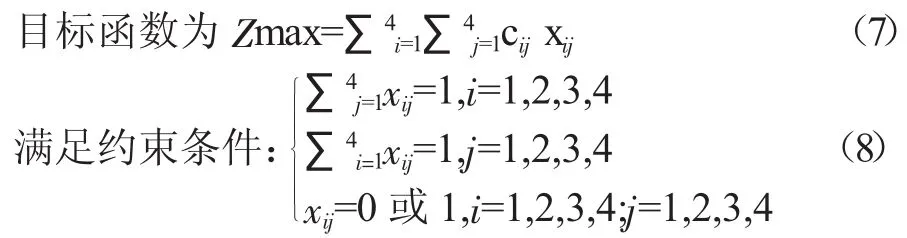
约束条件中第一个数学表达式的其含义为一个业务员只能负责一种产品的营销方案制作；约束条件中第二个数学表达式的含义为一种产品的营销方案只能一个业务员负责制作。

针对指派问题求解，传统数学建模教材中介绍的是匈牙利法求解，步骤繁琐。此处利用LINGO软件求解，方法同案例1所述，可得出最优的任务分派方案为:业务员1负责产品2的营销方案；业务员2负责产品4的营销方案；业务员3负责产品3的营销方案；业务员4负责产品1的营销方案，最大利润为27000万元。

随着数学软件的开发和使用，数学建模如虎添翼，广泛应用到现代物流活动的各个环节。围绕物流管理专业的人才培养目标，充分利用经典数学模型与物流实际问题的紧密联系，结合物流活动中的相关案例进行数学建模课堂教学，并选择简单、易学、快捷的lingo数学软件求解，不但能激发学生的内在学习动力，提高学生的数学建模能力和灵活运用数学建模解决问题的能力，更有助于学生职业能力和职业素养的提升。