扣件胶垫温变特性对车辆−轨道−桥梁耦合振动响应的影响研究

崔巍涛，刘林芽，秦佳良，左志远

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

近年来，我国高速铁路快速发展，轨道交通高架桥梁因其占地面积小、高平顺性和高稳定性得到了广泛应用，现已开通的京沪高铁与京津城际中桥梁比例达到了81%和77%，但是随之带来的振动与噪声问题也引起了人们的广泛关注[1−3]。扣件系统作为钢轨和下部结构的联结部分，其刚度和阻尼对轨道和桥梁结构的振动和噪声有重要影响[4−5]，张迅等[6]建立了有限元−边界元法箱梁结构噪声预测模型，研究扣件动参数对箱梁结构噪声声场分布和频谱特征；张燕等[7]采用动柔度法建立车−轨−桥频域分析模型，从频域角度研究扣件刚度对车辆、轨道和桥梁振动的影响。扣件系统主要由扣压件和弹性垫板组成，其中扣压件的刚度仅为0.5～1.2 kN/mm[8]，只占扣件刚度的很小一部分，同时扣压件的阻尼也非常小，故扣件垫板的刚度和和阻尼可近似看作整个扣件系统的刚度和阻尼。扣件垫板属于橡胶高分子材料，这类材料的动参数会因环境温度的改变而发生变化，具有明显的温度相关性[9−12]。我国地域辽阔，高速铁路运营范围广，极端气候明显，且部分地区昼夜温差大，扣件胶垫的温变特性会导致扣件的动参数发生变化，进而对车辆、轨道和桥梁的振动产生影响。目前，一些学者针对扣件胶垫的温变特性对轨道结构的振动影响进行了研究。翟志浩等[13]提出一种新型网孔式的弹性垫板，研究在低温时该铁路扣件对行车的安全性和平稳性的影响；韦凯等[14]以地铁常用的3种扣件为研究对象，研究扣件刚度的温变特性对轮轨耦合的频响特性影响，杨麒陆等[15]以Vossloh300扣件胶垫为实验对象，探究了扣件胶垫刚度的温变特性对高铁列车行车安全的影响；LIU等[16]通过对铁路扣件胶垫的变温定频试验，从频域角度研究扣件温变特性对车辆和轨道振动的影响。以往研究中大多只考虑了扣件胶垫动刚度的温变特性对车辆和钢轨振动的影响，但实际上扣件的动刚度和阻尼会随温度改变而同时发生变化，且以往研究均未考虑扣件动参数温变对轨道板和桥梁结构的影响。鉴于此，本文以高速铁路常用的WJ-7型扣件为研究对象，通过试验测得扣件的温变动参数，基于车辆−轨道−桥梁耦合动力学理论，采用自编程的车辆−轨道−桥梁垂向耦合振动的时域分析模型，对比不同温度下扣件动参数变化的时域响应和1/3倍频程转化后的频域响应，探究扣件垫板温变特性对车辆、轨道和桥梁振动的影响规律。

1 扣件胶垫温变特性试验

以我国高速铁路常用的WJ-7型扣件垫板为试验对象，采用橡胶动态力学分析仪对垫板进行温度扫描试验，激振频率为2 Hz，从−60℃扫描至40℃，每间隔2℃读取一次实验数据，试验对象和设备见图1。

图1 试验对象及设备Fig.1 Test object and equipment

将试验测得的扣件胶垫储能模量、耗能模量和损耗因子绘制成随温度变化的曲线，如图2所示。由图2(a)可知，扣件胶垫储能模量随温度的升高而不断减小，在−50℃以下变化较缓，在−50～40℃范围减小速率不断降低；耗能模量在−49.2℃左右达到峰值，在−49.2℃以下随温度的升高而增大，在−49.2℃以上随温度的升高而不断降低，减小的速率不断降低，可以发现储能模量和耗能模量在低温时比较敏感，高温时趋于稳定。图2(b)为扣件胶垫的损耗因子随温度变化曲线，损耗因子在−60～−45.7℃随着温度升高而增大，在−45.7℃以上则随着温度的升高不断减小，在−45.7℃左右达到峰值，这是因为该温度附近为材料从玻璃态向橡胶态转变的温度区间。

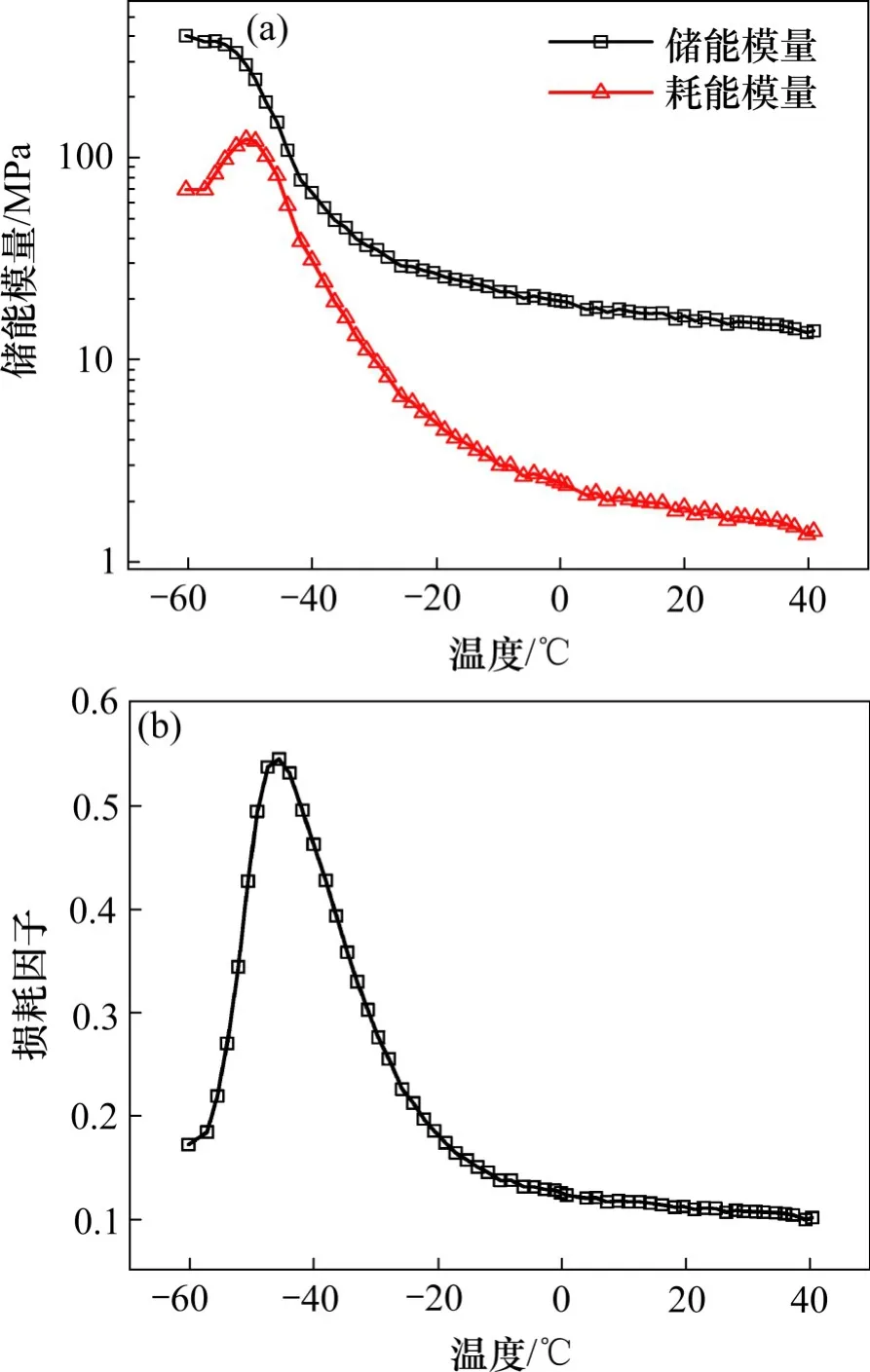
图2 弹性垫板温变动参数试验值Fig.2 Test value of temperature-dependent dynamic parameters of rail pads

在车辆−轨道−桥梁耦合时域分析模型中，常用刚度和阻尼2个动参数来表示扣件的性质，故需将试验测得的模量值和损耗因子进行转化。根据文献[17]，由试验得到的储能模量和损耗因子可以通过式(1)～(2)转化为耦合模型所需要的刚度和阻尼。

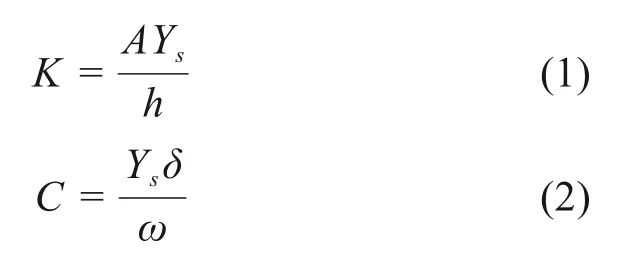
式中：K为扣件的刚度；C为扣件的阻尼；Ys和δ分别为扣件的储能模量和损耗因子；A和h依次为扣件胶垫的横截面面积和厚度。

因我国各地区的温度主要在−40～40℃范围内，故选择该温度范围计算扣件的动刚度和阻尼值，图3为转化后的动刚度和阻尼值。可以发现，刚度和阻尼具有明显的温度相关性，且低温时变化更为明显。

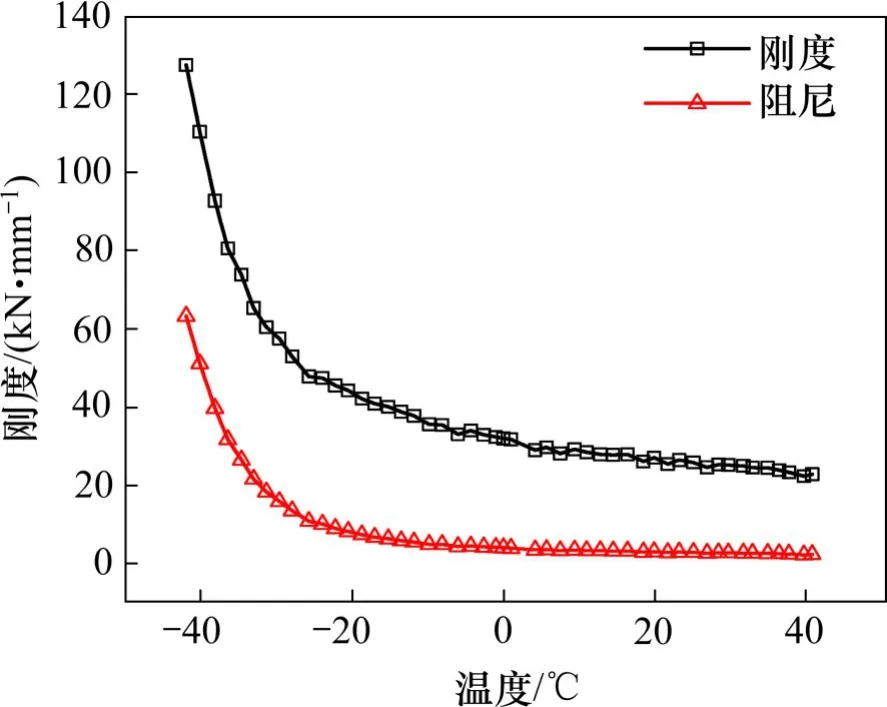
图3 弹性胶垫刚度和阻尼值Fig.3 Stiffness and damping value of rail pads

2 车−轨−桥耦合系统的时域计算模型

2.1 车辆−轨道−桥梁垂向耦合时域模型

图4为本文建立的车辆−轨道−桥梁耦合系统垂向模型，车辆和钢轨采用Hertz非线性弹性接触理论，钢轨与轨道板通过离散的扣件连接，轨道板和桥梁通过连续的CA砂浆层连接，底座板以参振质量的形式在桥梁模型中考虑。

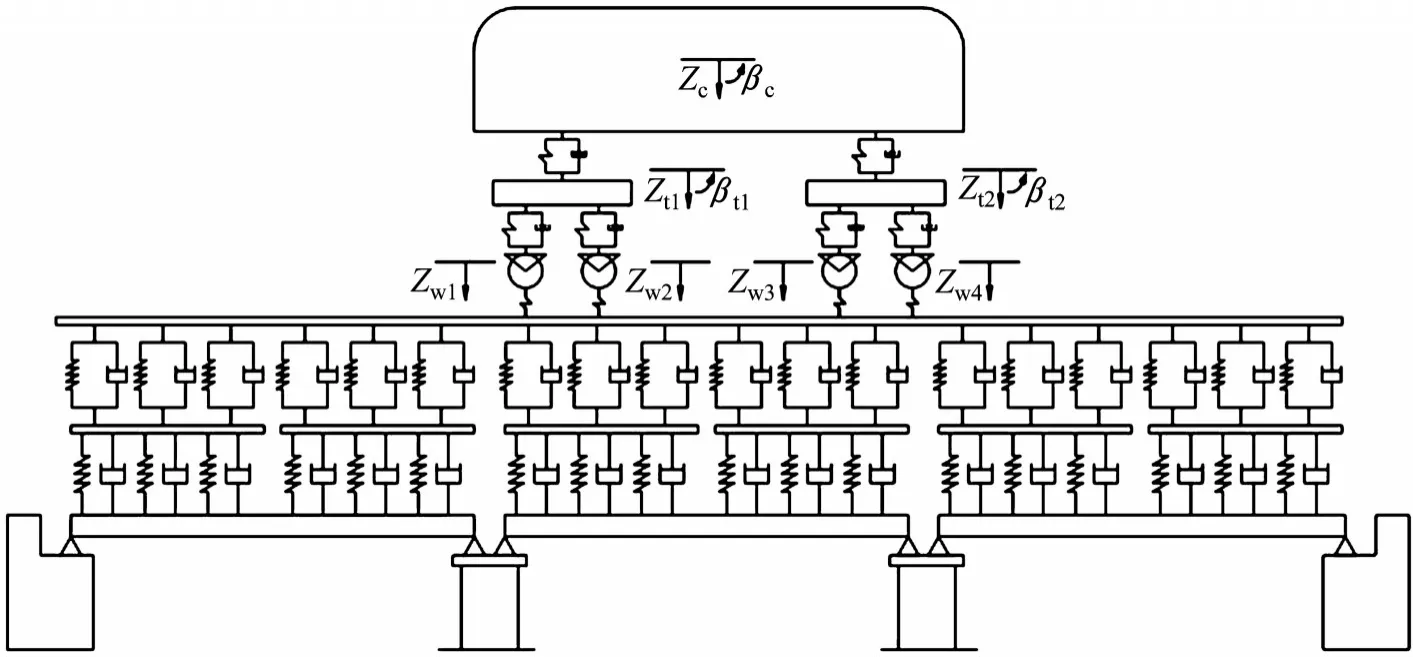
图4 车辆−轨道−桥梁耦合系统垂向模型Fig.4 Vertical model of vehicle-track-bridge coupled system

2.1.1 车辆模型

车辆系统考虑车体的沉浮和点头运动，前后构架的沉浮和点头运动，以及4个轮对的垂向振动共10个自由度[18]。车辆系统振动微分方程为

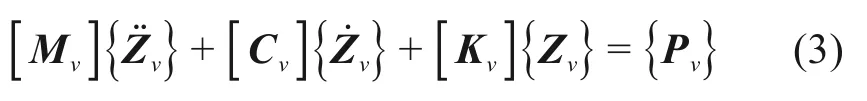
式中：[Mv]，[Kv]和[Cv]分别为车辆系统的质量矩阵、刚度矩阵和阻尼矩阵；和分别为车辆系统的位移向量、速度向量和加速度向量；{Pv}为车辆系统的广义力向量。

2.1.2 轨道模型

钢轨视为离散点支撑Euler梁，采用Ritz法求解，并引入钢轨正则振型坐标qk(t)，得到钢轨振型坐标的二阶常微分方程组为：

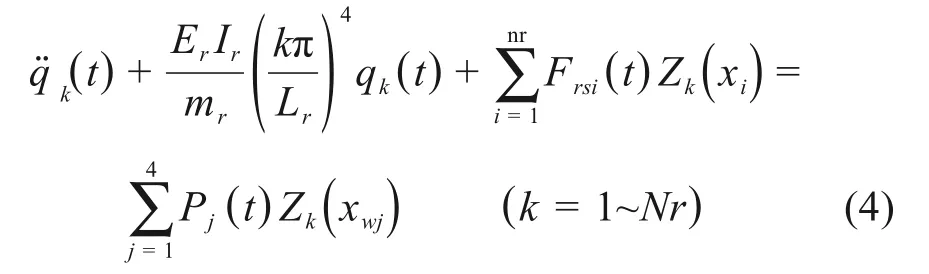
式中：Er，Ir分别为钢轨的弹性模量和截面惯性矩；mr，Lr为钢轨单位长度的质量和钢轨的总长度；Frsi(t)为第i个扣件位置处支反力；pj(t)为第j位轮轨作用力；xi和xwj分别为第i个扣件和第j个轮对沿线路纵向坐标；Zk(x)为钢轨的振型函数；nr为扣件的个数。

轨道板视为有阻尼的弹性基础上的两端自由梁，忽略板与板间的纵向连接，同样采用Ritz法求解，引入自由梁正交函数系{Xn}[18]，得到轨道板振型坐标2阶常微分方程组为：

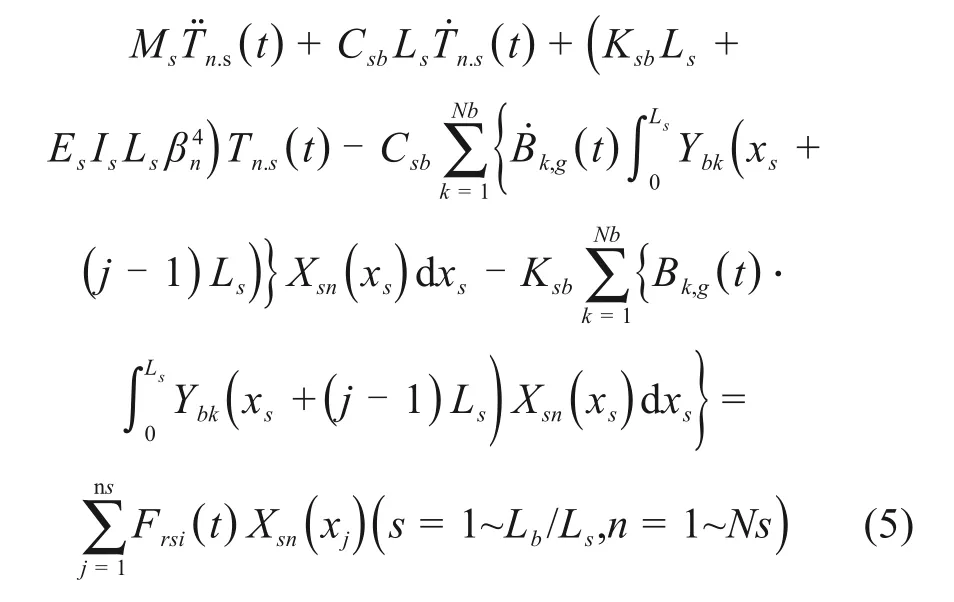
式中：Ms为轨道板的质量；Es，Is分别为轨道板的弹性模量和截面惯性矩；Ms为轨道板的质量；Ls为轨道板的长度；Ksb，Csb分别为轨道板下CA砂浆层沿长度方向的分布刚度和分布阻尼；ns为一块轨道板上的扣结点数；Zs(x,t)为轨道板的振动位移向量；Nb为桥梁的模态数；Ns为轨道板的模态数；Xsn(xi)为轨道板的自由梁正交函数系；Tn,s(t)为第s块轨道板的第n阶模态对应的广义坐标。

2.1.3 桥梁模型

桥梁同钢轨一样采用Euler梁模型，采用Ritz法求解，引入桥梁正则振型Bk(t)，化简得桥梁振型坐标微分方程组的详细形式为：

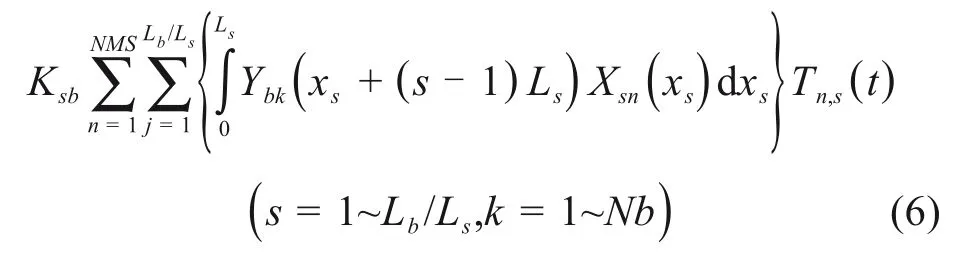
式中：Eb，Ib分别为桥梁的弹性模量和截面惯性矩；mb为桥梁单位长度的质量；ζ为桥梁的各阶阻尼比；ωbn为单跨桥梁的第n阶圆频率；Lb为一跨桥梁的长度；Yb,k(xi)为桥梁的振型函数；Bk,g(t)为第g跨桥梁的第k阶模态对应的广义坐标。

2.2 时域求解方法

将式(3)～(6)联立得到最终的车辆−轨道−桥梁耦合动力学微分方程组，采用新型显式积分法求解。其积分格式为

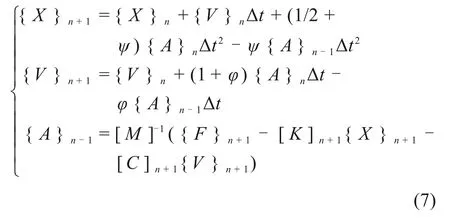
式中：ψ和φ为积分常数，取ψ=φ=1/2，Δt为积分时间步长，取0.1 ms；下标n-1，n和n+1分别代表第n-1，n和n+1时刻。初始条件设为{X}0={V}0={A}0={0}。

2.3 计算参数

本文列车采用CRH380高速客车，车辆参数见表1，轨道和桥梁的具体参数见表2。

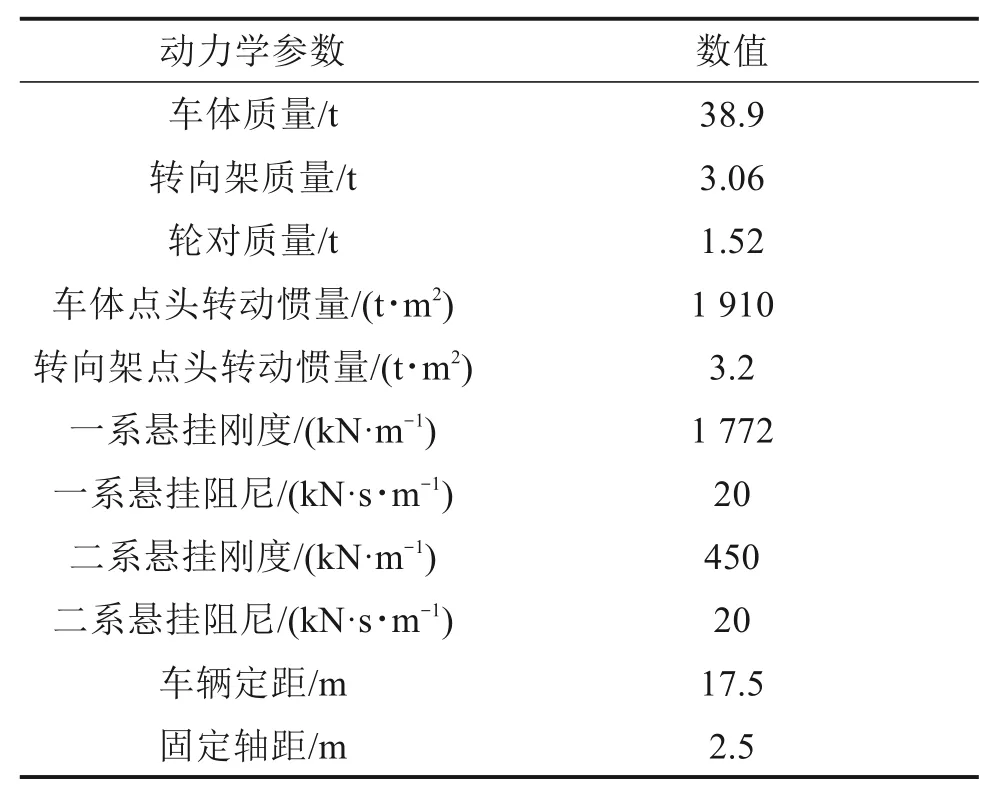
表1 CRH380高速客车的动力学参数Table 1 Dynamic parameters of CRH380 high speed train

表2 轨道和桥梁参数Table 2 Track and bridge parameters

本文以中国高速铁路无砟轨道的高低不平顺谱作为激励源[19]，列车运行速度为350 km/h，采用傅里叶逆变换法[20]获取不平顺的时域样本作为输入，见图5。

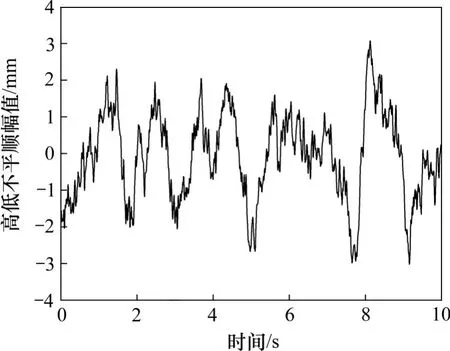
图5 中国高速铁路无砟轨道高低不平顺谱Fig.5 Power spectrum density of ballastless track irregularities of Chinese high-speed railway

3 扣件垫板温变特性对车辆−轨道−桥梁振动响应分析

根据温变试验结果，可以发现弹性垫板动参数在高温时变化较小，低温时变化较大，故选择弹性垫板在20，0和−30℃3种温度下的动参数来研究扣件胶垫温变特性对车辆−轨道−桥梁振动响应的影响，具体动参数见表3。应用上述模型和参数得到3种温度工况下车辆通过九跨简支梁的计算结果，对比分析车辆、轨道结构和桥梁动力响应，并采用1/3倍频程方法对比分析轮轨力和扣件力的频域结果。

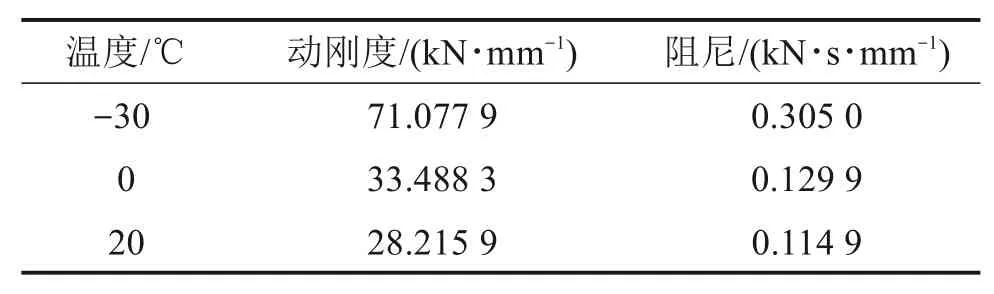
表3 计算工况Table 3 Calculated working condition

3.1 对车辆的影响

图6为不同温度下车体振动加速度的时频域对比。从图6(a)可以看出，车体垂向加速度均在−0.3～0.3 m/s2范围内变化且差别较小，远小于机车运行平稳性限值2.5 m/s2。从图6(b)可以看出，不同温度下车体振动加速度曲线几乎重合，主要集中在低频且峰值均在中心频率1 Hz，这是因为一系和二系悬挂隔绝了大部分的中高频振动。可以发现扣件动参数温变对车体的影响较小。

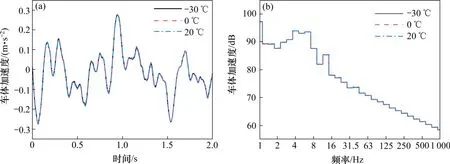
图6 不同温度下车体振动加速度Fig.6 Vibration acceleration of vehicle at different temperatures

3.2 对轮轨力和扣件力的影响

图7为不同温度下轮轨力的时频域对比。由图7(a)可知，温度为20℃时，轮轨力的最大值为92.489 kN，当温度从20℃降低到0℃时，轮轨力幅值整体增加，最大值为98.523 kN，增幅为7.61%；温度继续降低到−30℃时，轮轨力幅值普遍增大，最大值为103.597 kN，增幅为4.09%。文献[21]表明，扣件刚度增大会导致轮对力增大，本文也验证了这一观点。但当温度从20℃降低到0℃再到−30℃，轮轨力增幅减小，这是因为阻尼会随温度的降低而增大，导致轮轨力减小。同时考虑扣件刚度和阻尼的温变特性，轮轨力整体增大，说明在耦合振动中刚度温变特性的影响大于阻尼的温变特性。从图7(b)可知，随着温度的降低，轮轨力在中心频率16 Hz以下基本保持不变，在16～50 Hz和100～500 Hz范围内略微减小，在50～100 Hz范围内增大，轮轨力主频向高频偏移且峰值变大。

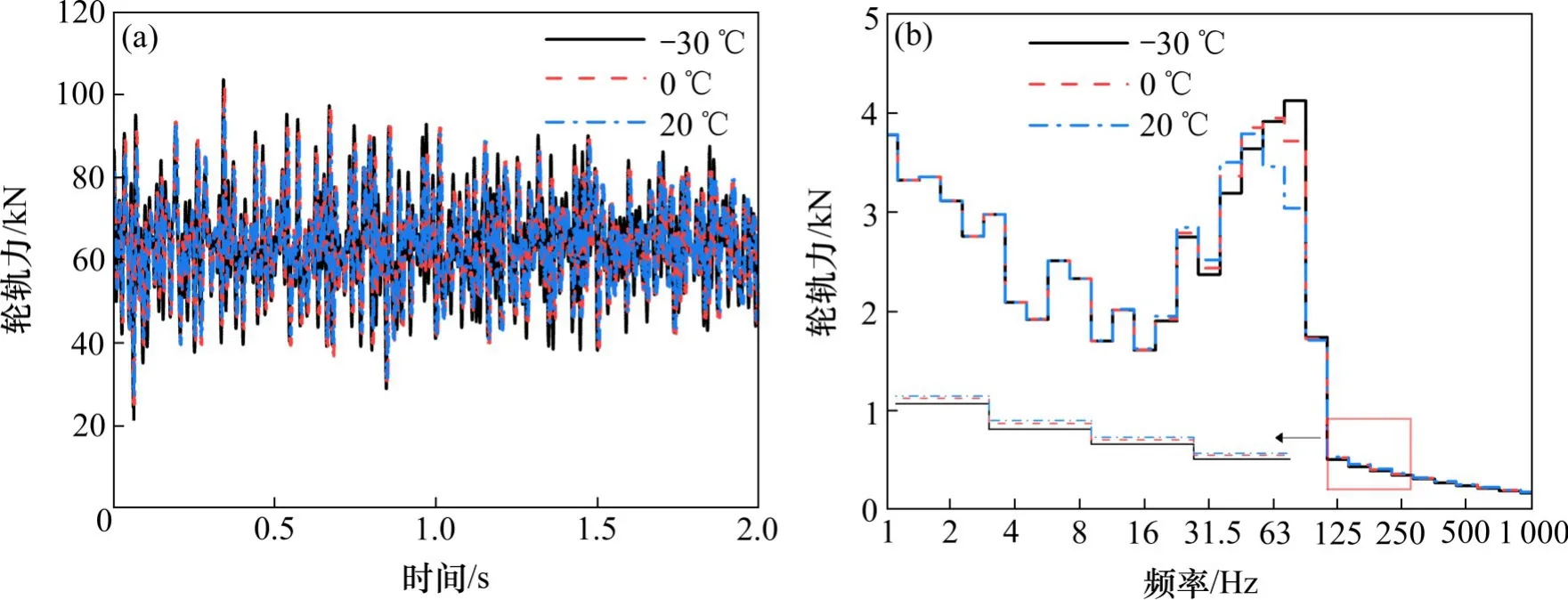
图7 不同温度下轮轨力Fig.7 Wheel-rail force at different temperatures

图8为不同温度下第5跨桥梁跨中扣件力的时频域对比。由图8(a)可知，温度为20℃时，扣件力的最大值为21.467 kN，降低到0℃时，扣件力增大，最大值为23.224 kN，增幅为8.18%；降低到−30℃时，扣件力继续增大，最大值为26.567 kN，增幅为14.39%。可以发现，随着温度降低，扣件力不断增大且增幅也变大，这是因为扣件刚度和阻尼随温度降低而增大，刚度和阻尼增大均会导致扣件力的增大，两者叠加导致扣件力明显增大。从图8(b)可知，随着温度降低，扣件力在16 Hz以下基本无变化，在16～200 Hz范围内有所增大，在中心频率31.5 Hz影响最为明显，当温度从20℃降低到−30℃，扣件力增大0.498 kN。

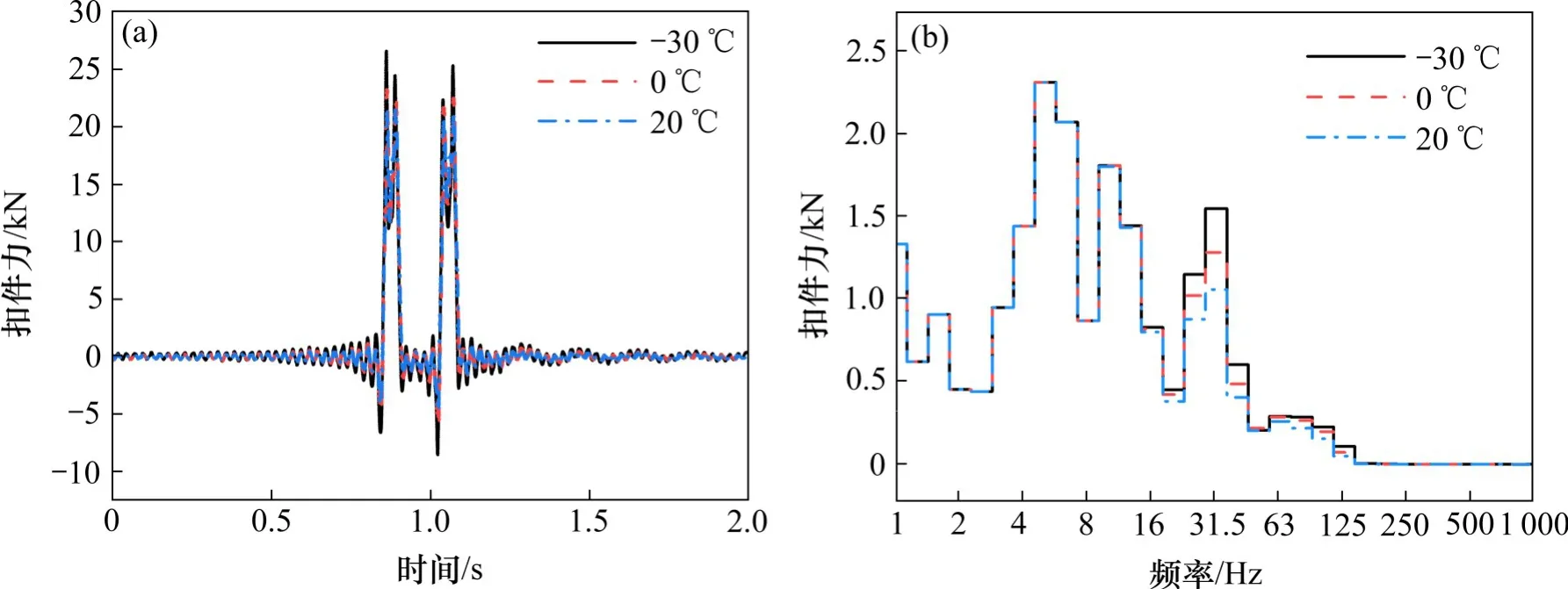
图8 不同温度下扣件力Fig.8 Fastener force at different temperatures

3.3 对钢轨的影响

图9为不同温度下的跨中钢轨相对桥面板的位移时程图。从图9可知，随着温度的降低，钢轨位移不断减小。当温度为20℃时，钢轨相对位移最大值为0.799 mm；温度降低到0℃时，钢轨位移最大值为0.626 mm，降低21.65%；温度继续降低到−30℃时，钢轨位移最大值为0.443 mm，降低29.23%，说明钢轨位移随温度降低而不断减小。

图9 不同温度下钢轨位移Fig.9 Rail displacement at different temperatures

图10为不同温度下的轨道板加速度时频域对比图。从图10(a)可知，当温度为20℃时，钢轨加速度最大值为21.28 m/s2；当温度降低到0℃时，钢轨加速度最大值为20.61 m/s2，降低3.15%；当温度继续降低到−30℃时，钢轨加速度最大值为17.98 m/s2，降低12.76%，说明温度降低会导致钢轨的加速度减小。从图10(b)可知，随着温度降低，钢轨加速度在8～125 Hz减小，在160～400 Hz增大，钢轨加速度主频在63 Hz附近，这与轮轨耦合共振有关。

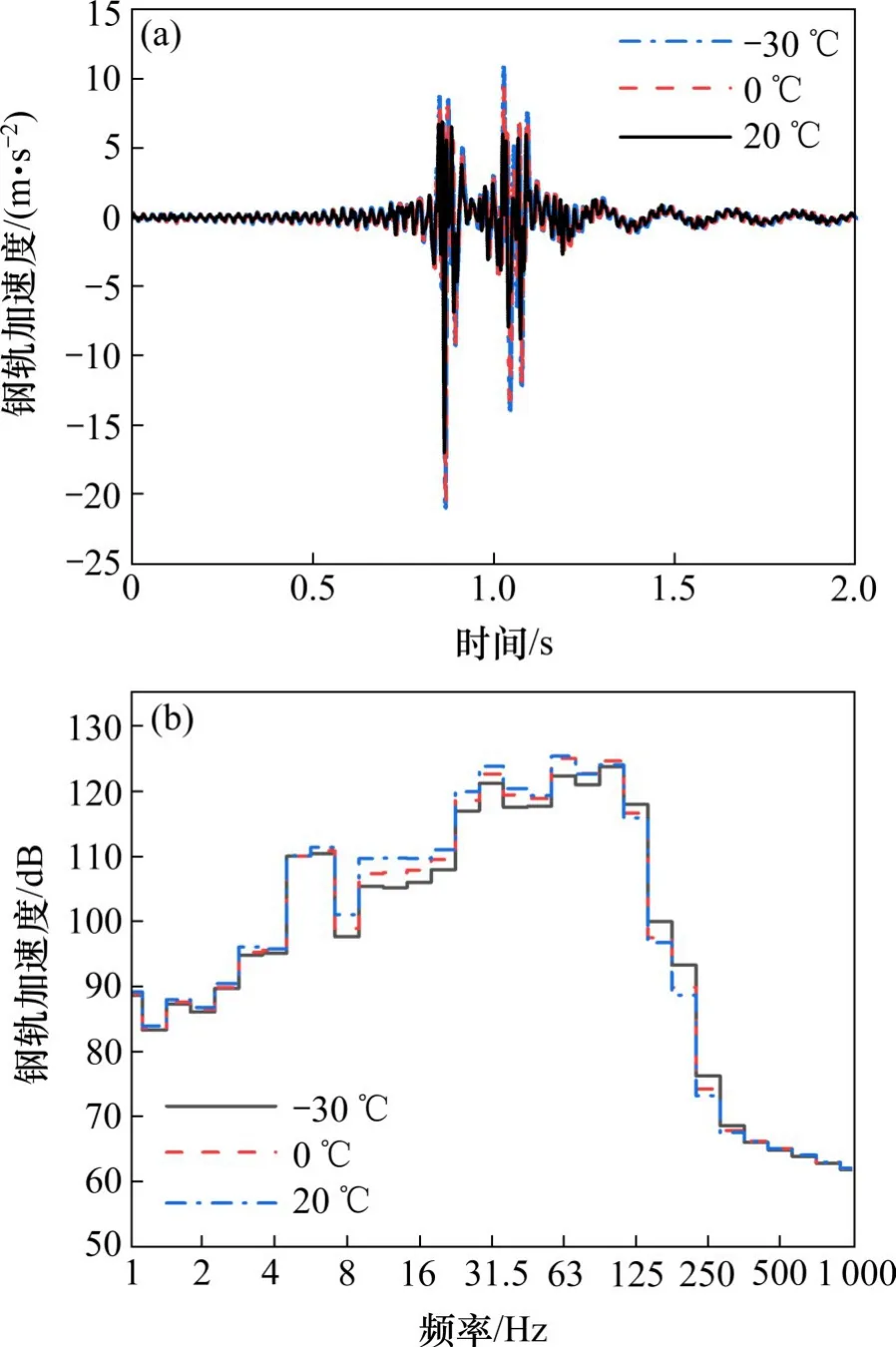
图10 不同温度下钢轨加速度Fig.10 Rail acceleration at different temperatures

3.4 对轨道板的影响

图11为不同温度下的第5跨桥梁跨中轨道板相对桥面板的位移图。从图11可知，当温度分别为20，0和−30℃时，轨道板相对位移最大值分别为0.103，0.108和0.112 mm，轨道板位移随着温度的降低而略微增大。

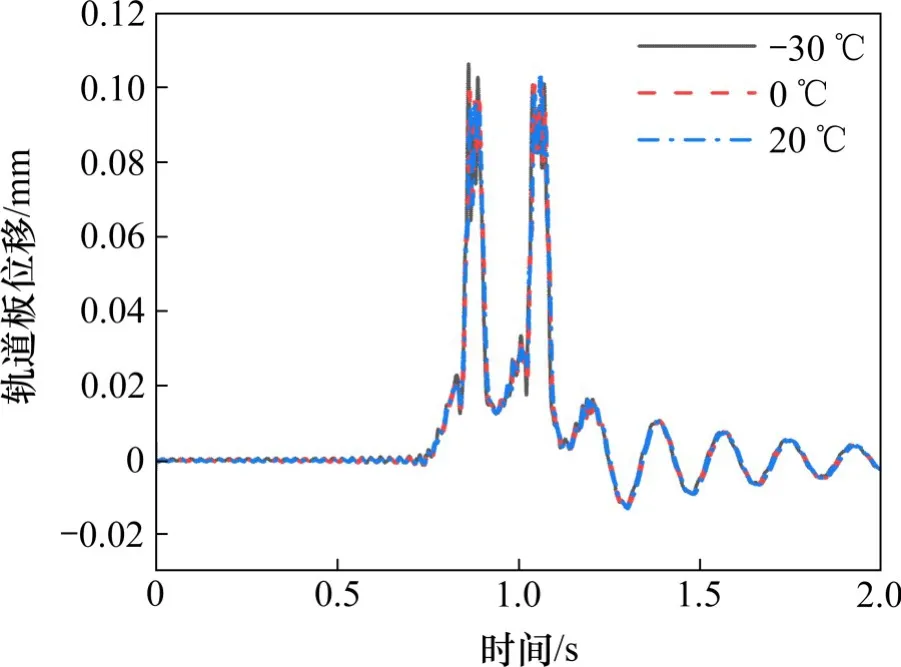
图11 不同温度下轨道板位移Fig.11 Track slab displacement at different temperatures

图12为不同温度下轨道板的加速度时频域对比。从图12(a)可知，随着温度的降低，轨道板加速度不断增大。当温度为20℃时，轨道板加速度最大值为3.078 m/s2；当温度为0℃时，轨道板加速度最大值为3.821 m/s2，增大24.14%；当温度为−30℃时，轨道板加速度最大值为5.368 m/s2，增大40.49%。由图12(b)可知，当温度降低时，轨道板加速度在20 Hz以下基本无变化，在20～63 Hz范围内变化较小，在80～400 Hz明显增大，在主频100 Hz处增大3.85 dB，说明扣件动参数温变主要影响轨道板的中高频振动，随温度的降低轨道板的中高频振动加剧但主频不变。

3.5 对桥梁的影响

图13为不同温度下的第5跨桥梁跨中位移图。从图13可知，3种温度下桥梁位移曲线图吻合较好，说明扣件动参数温变对桥梁垂向位移几乎没有影响。

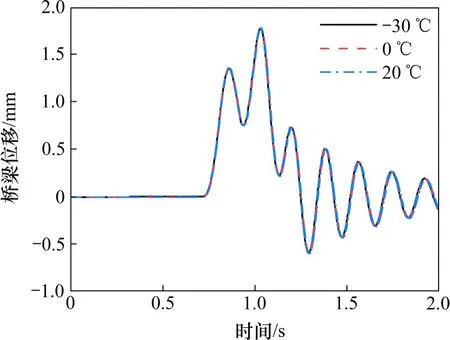
图13 不同温度下桥梁跨中位移Fig.13 Mid-span displacement of bridge under different temperatures

图14为不同温度下的第五跨桥梁的加速度时频域对比。从图14(a)可知，随着温度的降低，桥梁加速度有所增大。当温度为20℃时，桥梁加速度最大值为2.910 m/s；当温度降低到0℃时，桥梁加速度最大值为2.968 m/s2，增大1.99%；当温度继续降低到−30℃时，桥梁加速度最大值为3.122 m/s2，增大5.19%。从图14(b)可知，随着温度降低，桥梁加速度在63 Hz以下变化较小，在80～250 Hz明显增大，与轨道板加速度变化规律类似。

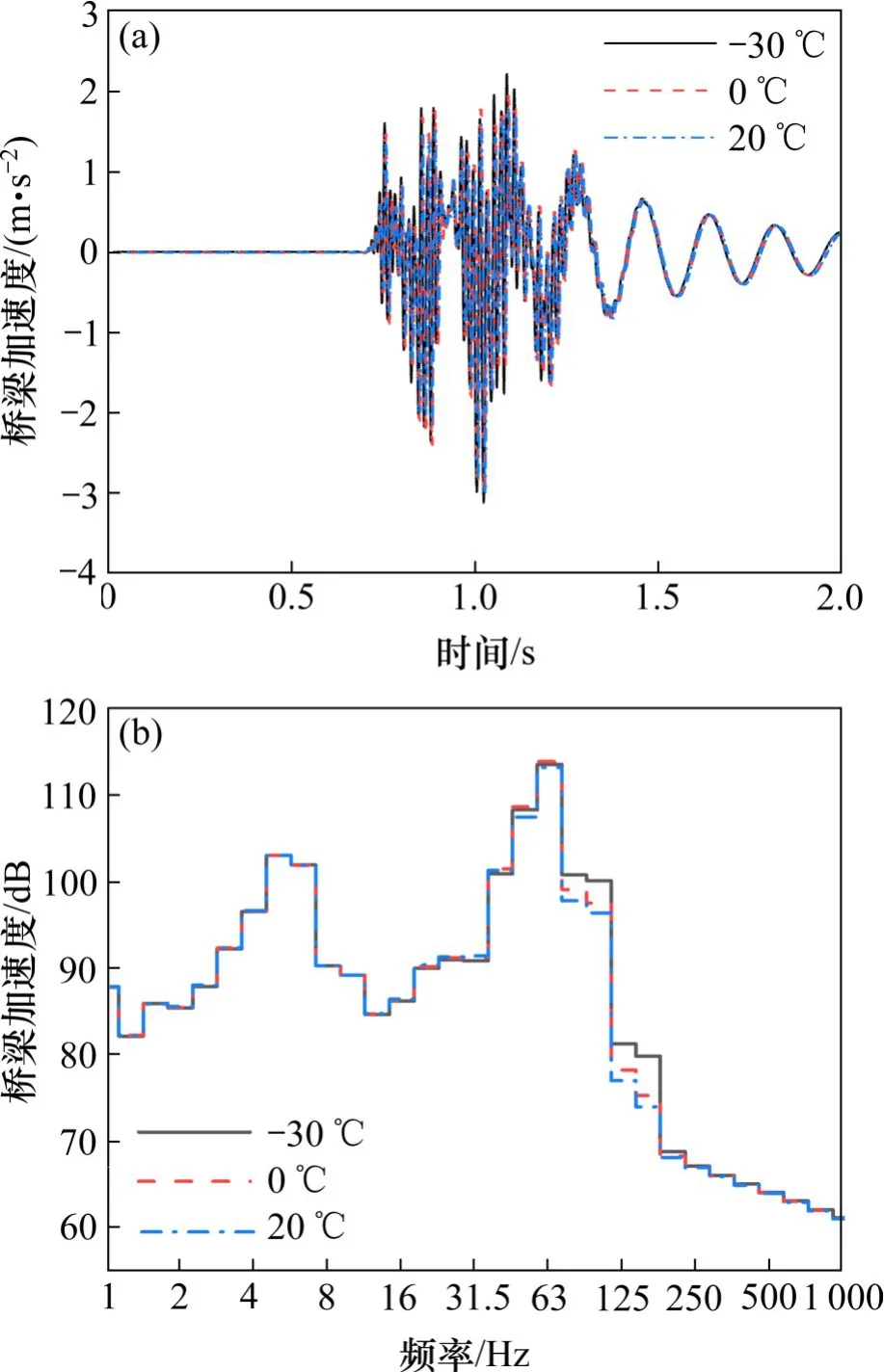
图14 不同温度下桥梁加速度Fig.14 Bridge acceleration at different temperatures

4 结论

1)扣件胶垫的动刚度和阻尼具有明显的温度相关性，均随温度的降低而不断增大，在低温时增幅明显，耦合振动分析中应同时考虑。相比于20℃，−30℃时弹性垫板的动刚度和阻尼值分别增大了1.52倍和1.74倍。

2)扣件动刚度和阻尼温变特性对轮轨力和扣件力影响明显，随着温度的降低，相比于20℃，−30℃时轮轨力和扣件力分别增大12.01%和23.76%，轮轨力的主频向高频偏移且峰值增大，扣件力在中心频率31.5 Hz附近峰值有明显增大。

3)从时域响应来看，扣件动刚度和阻尼温变特性对车体垂向振动加速度和桥梁位移几乎无影响。随着温度降低，轮对加速度、轨道板加速度、和桥梁加速度不断增大，相比于20℃，−30℃时分别增幅18.10%，40.49%和7.29%。随着温度的降低，钢轨的位移和加速度有所减小，相比于20℃，−30℃时分别降低了44.56%和15.51%。

4)从频域响应来看，扣件动刚度和阻尼温变特性对车体振动基本无影响。随着温度降低，钢轨振动在8～100 Hz范围内减小，在125～315 Hz增大。轨道板在80～400 Hz范围内振动加剧，桥梁在80～250 Hz振动加剧，其他频段变化不明显。

本文采用自编程序建立了车辆−轨道−桥梁垂向耦合振动分析模型，研究了扣件垫板的温变特性对车辆、轨道和桥梁结构振动的影响。一般来说，轨道板和桥梁结构在环境温度变化时自身也会产生变形，且影响机理和规律较为复杂。本文构建的二维模型暂无法同时考虑温度变化时轨道板和桥梁结构的变形，因此研究结论尚有一定的局限性，下一阶段将结合仿真分析软件建立精细化的三维模型进行深入研究。