运营隧道原型-模型衬砌应力理论模型及应用

陶永虎，饶军应，熊 鹏，聂崇欣，谢财进

(贵州大学 土木工程学院，贵州 贵阳 550025)

近年来，随着经济的高速发展，各类岩土工程、边坡工程及隧道工程等项目建设愈发频繁，而工程事故也随之增多，尤其在隧道建设方面，由衬砌变形、漏水、内应力增大等原因引起的事故不计其数[1-4]。目前，大多数施工单位都是通过布设测点测量衬砌变形情况来预判隧道安全与否，但此方法只能大概估计衬砌应变情况，误差较大，故准确判断已建隧道衬砌应力变化对隧道的安全使用是非常必要的。若能建立原型-模型衬砌应力理论模型，通过模型衬砌应力变化反映实际衬砌应力变化，那么就能从理论上准确掌握隧道衬砌应力变化情况，及时采取补救措施，这不但节省了劳动力，同时还保证了隧道运营安全[5-10]。

在原型与模型试验研究方面，朱叶艇等[11]进行了异形盾构隧道衬砌应力计算模型及受力特性研究，得到了衬砌应力计算的分析模型，但在原型-模型衬砌应力之间未给出明确的理论关系；江浩等[12]研究了几何相似比对模型试验及原型试验隧道衬砌内力的影响，总结出相似比的变化对衬砌应力变化影响显著，但未从隧道受力方面给出模型衬砌应力的具体计算方法；张鹏[13]利用模型试验研究海底隧道衬砌应力变化规律，根据相似准则建立模型试验，总结出衬砌应力与流固耦合之间存在较大关系，但在理论研究方面，没有明确给出其理论计算模型；景诗庭[14]利用模型试验研究衬砌应力变化，分析了原型-模型试验之间的区别，但未从理论上给出其计算方法；刘金云等[15]进行了流固耦合下的输水隧道动力模型试验研究，发现通过数值模拟，模型试验衬砌应力结果可反映到原型试验值上，但未从理论方面进行研究解释。综上所述，目前关于模型-原型试验的研究主要集中于相似材料、模型与原型关系、几何相似比对模型的影响等方面，并通过数值模拟来反映衬砌应力变化，但参数选择及材料假定会给数值模拟带来一定的偏差，导致模拟结果模棱两可，故从理论方面研究原型-模型衬砌应力关系是很有必要的，这既能纠正数值模拟的偏差，也能为衬砌应力计算提供理论方法。

本文在前人研究基础上，利用相似原理建立原型-模型衬砌应力关系，通过复变函数保角变换将双连拱隧道衬砌转化为两个相切的圆环，通过假定应力解析函数及位移解析函数对变换的模型进行应力求解，最后再根据已建的应力关系，得到化简后的原型-模型衬砌应力理论计算模型，并对模型进行化简及分析。

1 模型构建

1.1 原理介绍

这里视隧道衬砌为薄板结构，本模型试验采用静态平面应变模型。隧道衬砌相似条件主要依据弹性力学本构关系，若以下标N和M分别表示原型和模型的物理量，则原型和模型都应满足弹性力学的基本方程[16]：

1)平衡微分方程

原型：

(1)

模型：

(2)

2)相容方程

原型：

(3)

模型：

(4)

3)物理方程

原型：

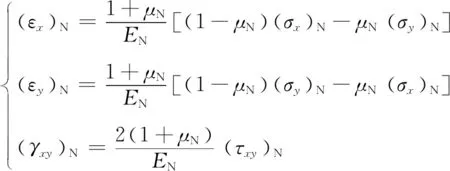
(5)

模型：

(6)

4)几何方程

原型：

(7)

模型：

(8)

5)边界条件

原型：

(9)

模型：

(10)

通过假定材料几何相似比，由式(1)～(10)可以确定模型试验的相似参数。

1.2 模型参数设定

由于双连拱隧道衬砌受力较为复杂，且假设衬砌材料均为弹性连续介质，故采用方程分析法确定相似常数。根据方程分析相似准则，设ξ表示相似常数，将其分别代入式(1)～(10)。

依据式(1)得：

(11)

同理,将ξσ、ξL、ξε、ξE代入式(3)～(10)得：

(12)

(13)

(14)

(15)

已知相似比时，便可通过式(11)～(15)求得其他相似常数，从而确定原型应力与模型应力之间的数量关系。

1.3 原型-模型衬砌应力关系构建

由相似试验可知，模型衬砌应力与原型衬砌应力之间相差一个常数关系，为求得模型与原型衬砌应力之间的关系，现将连拱隧道看作是一个平面应变问题，只在x、y方向受均布压力，其计算原型如图1、图2所示。

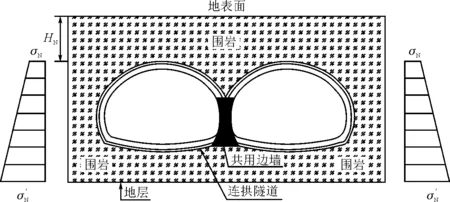
图1 原型连拱隧道自重应力场分布Fig.1 Self-weight stress field distribution of the prototype double-arch tunnel

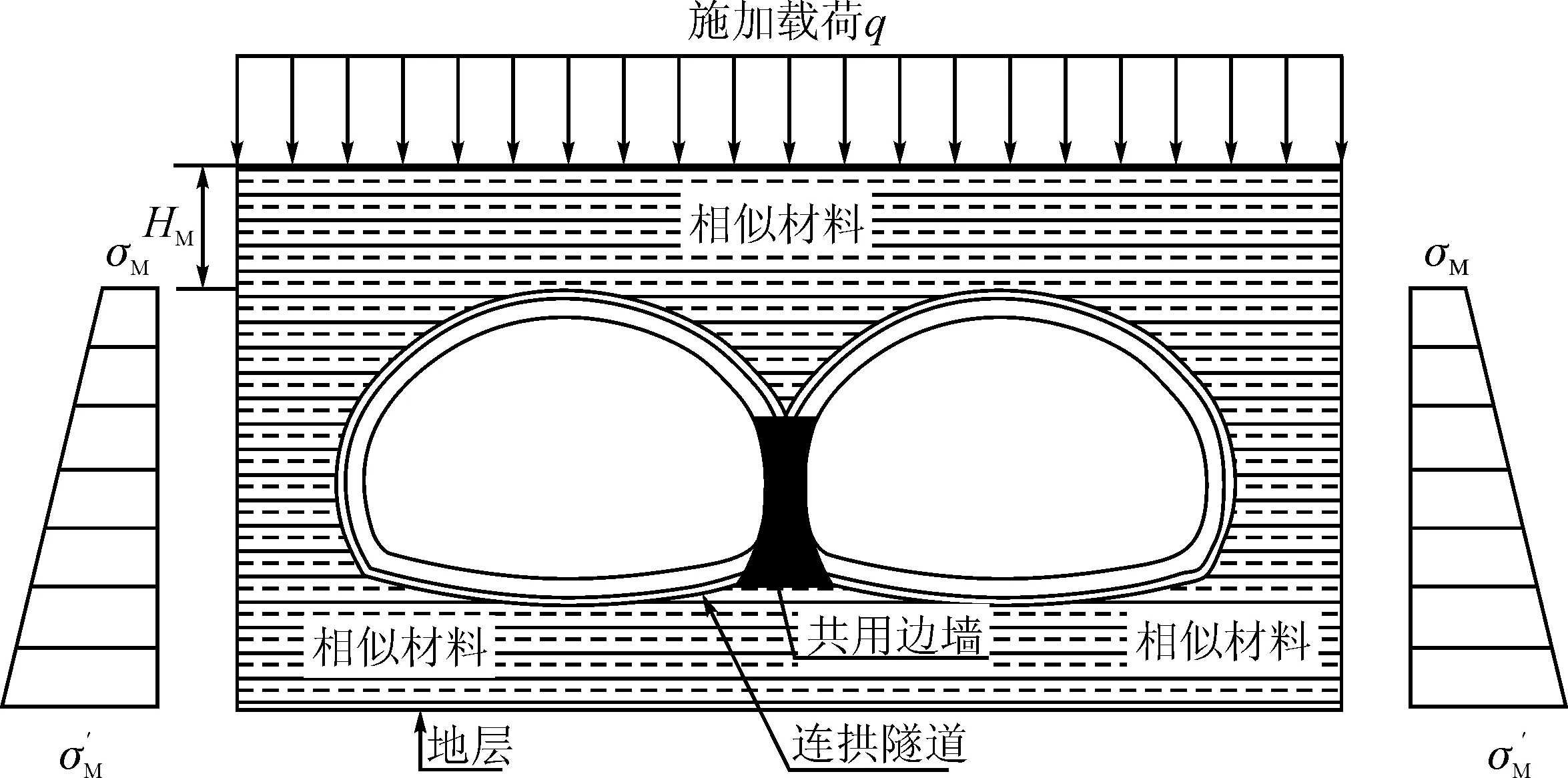
图2 等效模型施加外加应力的应力分布Fig.2 Stress distribution of equivalent model applied stress

1.4 原型-模型衬砌应力关系

1.4.1σN与σM关系的建立

在非两拱共用边墙部位，隧道衬砌受力较两拱连接处简单，采用弹性力学本构方程进行求解，其计算模型如图3所示。假设衬砌薄板均布压力为q，惯性矩为W，K为弯曲刚度，板厚为t。

图3 薄板受力Fig.3 Force of thin plate

根据材料力学薄板弯曲挠度方程[17]：

∇∇2δ=0

(16)

对应在直角坐标方程中，则有：

(17)

式中：δ为薄板发生弯曲时产生的挠度；∇表示哈密顿算子。

假设该隧道的几何相似比ξL=1/λ，弹性模量EN=EM，泊松比μN=μM，依据式(11)～(15)得：

(18)

再由式(11)～(15)可以得到原型与模型相关计算指标的关系：

(19)

原型与模型薄板弯曲方程：

(20)

由式(18)～(20)解得：

(21)

若EN=EM、μN=μM则：

(22)

若，则：

即：

(23)

由式(23)可知，模型衬砌应力与原型衬砌应力存在理论关系，通过确定模型衬砌应力，便可知道该隧道衬砌的受力情况及变化规律。

1.4.2模型应力σM复变解

在求解无中墙连拱隧道衬砌应力时，将其视为无限平面中的孔口问题，忽略边界条件及地应力的变化[18]。衬砌问题是一个多连通域问题，其边界由围岩、隧道衬砌、空气组成，而本文在计算衬砌应力时，利用复变函数保角变换思想，将隧道衬砌假设为连续相切的圆环，依据复变函数[19-22]幂级数展开及结合边界条件便可求得其隧道衬砌应力，该变换模型属于三连通域问题。该隧道模型关于边墙中心对称，故受力相同，下文均只取变换后的左圆环进行应力计算，其计算图如图4所示(其中ρ、θ表示极坐标下的极径、旋转角，a、b表示保角变换后的衬砌内径、衬砌外径)。

图4 Γ平面保角代换为φ平面示意图Fig.4 Schematic diagram of Γ plane conformal substitution to φ plane

Γ平面中，C1、C′1与C2、C′2分别为左幅隧道和右幅隧道的围岩与衬砌；P1、P′1分别表示左幅隧道与右幅隧道衬砌与大气的接触面；P2、P′2分别表示左幅隧道与右幅隧道衬砌与围岩的接触面，满足衬砌与围岩接触时的连续边界条件。由Γ平面通过保角代换得φ平面圆环结构，其中C1、C′1、C2、C′2区域映射为φ平面的Z1、Z′1、Z2、Z′2区域；P1、P1′、P2、P′2区域映射为φ平面的ω1、ω′1、ω2、ω′2区域。

设χ(Γ)、ψ(Γ)分别为应力解析函数、位移解析函数，则各计算指标用复函数表示为：

应力分量：

(24)

位移分量：

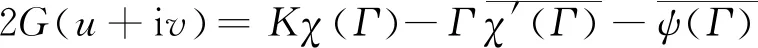
(25)

在P1边界面，其边界条件为：

(26)

在P2边界面，其边界条件为：

(27)

式中：u、ν分别表示围岩水平和竖向位移；fx、fy分别表示x、y方向的面力；A为弧长起算点，F为边界上任一点；C为弧长起算点，D为边界上任一点；G为剪切模量，G=E/(1+2μ)；μ为泊松比。

在双连通域中，其应力解析函数和位移解析函数的形式为：

(28)

式中：χ*(Γ)为ρ=1单连通域的应力单值解析函数；ψ*(Γ)为ρ=1单连通域的位移单值解析函数；m为边界值。

利用复变函数共性映射原理求解复杂平面问题时，常将复杂的计算截面通过保角代换为规则的几何形状进行求解，结合应力和位移边界条件进行计算。由于隧道衬砌受力问题可以理解为平面应变孔口受力问题，故将式(28)做如下化简：

取映射函数Γ=Φ(φ)=b/ζ，φ=ρ(cosθ+isinθ)=ρeiθ，从而得到φ平面的极坐标复变函数方程：

(29)

其中：

(30)

式中：M、M′、F′为无穷远处应力常数；mk、sk为边界面上某一点；ζk为幂级数展开关于ζ的项；bk表示常数b在第k序号时对应的幂；k为大于0的正整数，k=3-4μ。

在极坐标下，应力分量：

(31)

利用Laurent幂级数进行求解，将χ(Γ)、ψ(Γ)在φ平面上展开：

(32)

式中：α0和η0分别表示初始地应力及初始位移。

对于该隧道模型，在φ平面上有三个应力边界，且在三个边界面均不考虑面力，即当ρ=1、ρ=a、ρ=b时，有：

假设隧道左侧和右侧最大荷载为q1，拱顶最大荷载为q2，由式(28)～(32)结合边界条件化简可得：

(33)

由式(33)可得其衬砌所受应力关系，通过参数的确定便可求得衬砌在各个方向的应力值，结合式(23)就可得到原型-模型的衬砌应力关系。

2 模型化简及分析

2.1 模型化简

由于式(23)是直角坐标下的方程，式(33)是极坐标下的应力方程，为了便于计算，进行相应坐标变换，变换公式为：

(34)

σρ+σθ、σρ-σθ计算如下：

(35)

将式(35)代入式(34)得到：

(36)

式(36)较为复杂，而真实修建隧道时，只考虑最大衬砌应力的影响(应力过大，容易引起衬砌开裂、渗水)，为安全起见，现对模型进行如下简化：根据弹性力学可知σρ+σθ=σx+σy，根据保角代换可知当θ→0时，相应的β→0，此时对应的衬砌应力为边墙应力最大值，拱顶最大荷载q2几乎为零，这时ρ近似为B(边界值)，衬砌应力为：

(37)

式(37)即为右边墙受到的应力情况，符合隧道在边墙处的衬砌受力情况。

当θ→π时，相应的β→π，此时不考虑拱顶最大荷载q2，左边墙衬砌受力为：

(38)

当θ→π/2时，相应的β→π/2，此时不考虑边墙最大荷载q1，拱顶部位衬砌受力为：

(39)

式中：h为隧道净高。

根据式(23)及式(37)～(39)建立组合模型，其结果为：

当θ→0，β→0时：

(40)

当θ→π，β→π时：

(41)

当θ→π/2，β→π/2时：

(42)

式(40)～(42)即为隧道衬砌受力的三种极端情况，保证三种应力安全情况下，隧道偏于安全。

2.2 误差分析

为分析该理论模型的误差变化情况，现做如下计算：

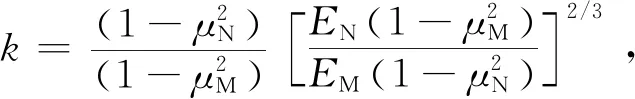
y*-y=k(x*-x)

记e(y)=y*-y，e(x)=x*-x，则有：

e(y)=ke(x)

由Taylor公式展开得到绝对误差及相对误差：

(43)

将已知条件代入式(43)得：

(44)

式(44)即为该模型的误差表达式，只要知道其相似参数，便可确定其误差范围。

3 典例分析

本文依托于云南大理某连拱隧道，其右幅K37+750～K38+205段(左幅ZK37+742～ZK38+180段)地形起伏较大，右幅全长455 m(左幅438 m)，最大埋深64.76 m。隧道区海拔高程1 743～1 817 m，相对高差74 m，属构造剥蚀中山地貌区。隧道区地形较为陡峻，地表植被发育较好。隧道围岩等级为Ⅴ级，围岩较破碎，风化岩较多。

该模型的相关相似常数为ξL=25、ξγ=1、ξε=ξμ=1、ξR=ξσ=ξC=ξE=25(ξR、ξC为强度相似常数、粘聚力相似常数)，其相关的物理力学参数及相似材料力学参数如表1所示。其测点布置如图5所示，由于隧道左右幅受力情况相同，现取左幅隧道进行衬砌应力分析，原型-模型相关参数如表2所示，理论值与原型测量值相关参数如表3所示。原型-模型衬砌应力如图6所示。

表1 隧道物理力学参数Tab.1 Parameters of prototype tunnel

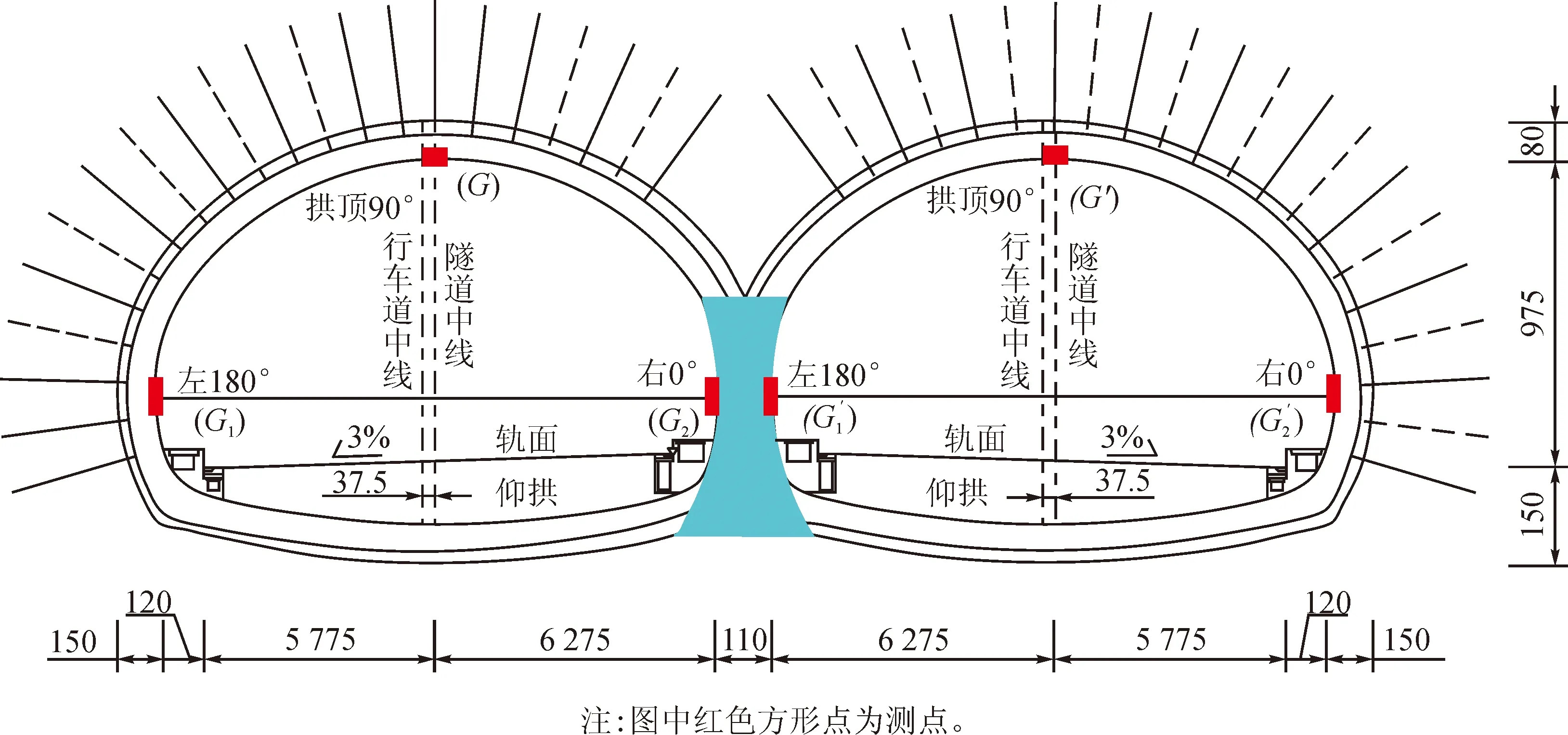
图5 测点布置示意图(单位：cm)Fig.5 Schematic diagram of measuring point layout (unit:cm)

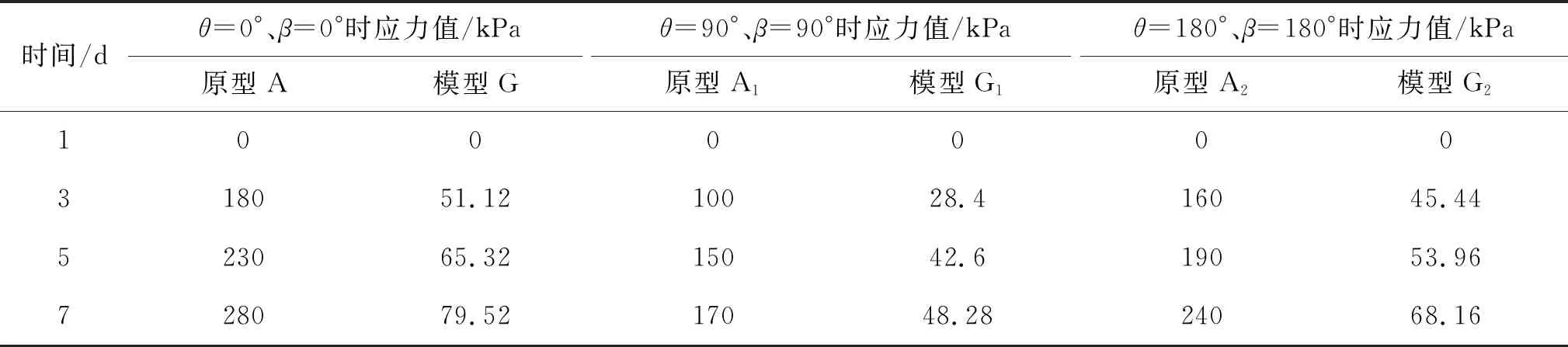
表2 模型实测值与原型实测值之间的关系Tab.2 Relationship between model measurement value and prototype measurement value

表3 原型实测值与模型理论值之间的关系Tab.3 Relationship between prototype measured value and model theoretical value

图6 原型-模型衬砌应力示意图Fig.6 Schematic diagram of prototype-model lining stress

由图6(a)可知，模型实测值与原型实测值变形趋势相同，均随着时间增加，且σN/σM≈0.31；当1d～3d时，原型与模型的衬砌应力均随时间大幅增加；当3d～7d时，模型与原型衬砌应力虽随时间增加，但变化幅度较小。

由图6(b)可知，模型理论计算值与原型实测值均随时间增加，且其变化趋势一致，说明模型理论值与原型实测值较为接近，表明该理论方法合理可行；理论值与实测值之间最大误差为5.02%，最小误差为0。

4 结 论

1)本文基于相似原理，构建了原型-模型的衬砌应力关系计算模型，其原型衬砌应力与模型衬砌应力之间相差一个常数，此常数可通过相似材料及围岩物理力学参数来确定。

2)连拱隧道受力较为复杂，采用复变函数保角代换求解模型应力，理论化简得到原型-模型衬砌应力关系，经围岩压力计算可分别得到q1、q2，从而可通过模型应力反推原型实际衬砌应力。

3)经模型化简、误差分析可得高应力区模型-原型衬砌应力理论关系，该模型产生的绝对误差较小，最大误差为5.02%，最小误差为0。

4)经分析，原型实测值与模型实测值均随时间增加，其变化趋势一致，且σN/σM≈0.31；原型实测值与模型理论值较为接近，且均随时间增加。该结果验证了模型的合理性，说明根据模型值反推原型隧道衬砌应力是可行的。

5)本文未考虑地下水压力、地应力的影响，后续研究会将其纳入考虑，以便分析其对衬砌应力变化的影响。