非均匀张力作用下斜支承运动薄膜的振动特性研究

邵明月，王 静，武吉梅，庆佳娟

(西安理工大学 印刷包装与数字媒体学院，陕西 西安710054)

薄膜作为一种常见的承印材料在柔性电子印刷及卷到卷制造中得到了广泛应用。在传输过程中薄膜由多个牵引辊以及导向辊支承，当薄膜传输方向需要改变时通常采用斜支承辊，斜支承辊的支承作用以及辊与辊之间的安装误差所引起的张力不均情况[1]都会改变运动薄膜的振动特性，导致印刷过程中产生套印不准等故障，引起较大的印刷误差。因此，研究非均匀张力作用下斜支承运动薄膜的振动特性对优化印刷设备，提高印刷质量具有重要意义。

目前，已有部分学者分别对非均匀张力作用下运动材料的振动问题及具有支承的轴向运动系统进行研究。王砚等[1-2]分别基于解析法和微分求积法对非均匀张力作用下的运动薄膜稳定性进行研究。Banichuk等[3]的研究表明较小的张力不均匀性会对薄膜的发散形式产生较大影响。Nguyen和Hong[4]在考虑薄膜非均匀张力的基础上提出了一种用于控制轴向运动薄膜系统振动的新颖算法。Ma等[5]对张力呈抛物线分布的轴向运动薄膜横向振动稳定性进行研究，结果表明较小的非均匀张力就会对薄膜的振型有影响。武吉梅等[6-7]采用次最优控制法对非均匀张力作用下的运动薄膜振动进行控制并对中间支承运动薄膜振动特性进行研究。马亮[8]考虑了柔性基板非均匀张力以及中间弹性支承影响，对柔性基板卷到卷输送中横向振动特性、振动控制及应用进行分析，结果表明变张力系数对基板内应力分布有较大影响。Liew等[9]在考虑多种边界条件情况下研究了带有内部斜支承矩形板的自由振动。Lai等[10]将DSC-Element法应用于斜板的自由振动分析，验证了DSC-Element法的有效性并得到具有混合边界条件斜板的频率解。Ketabdari等[11]通过参数研究，分析不同边界条件、偏斜角、非均匀性因子及变弹性基础刚度对斜板自由振动的影响。Parida[12]和Ramu[13]分别对功能梯度材料斜板的振动特性进行研究。郭旭侠和薛晓飞[14]基于微分求积法对热弹耦合运动斜板的振动特性进行研究。Kuma[15]等应用有限元法对斜夹层板的自由振动进行研究。胡寒和聂国隽[16]研究了变角度纤维复合材料层合斜板的颤振，采用Ritz法得到了层合板的自振频率和颤振不稳定的临界速度。

综上所述，目前的研究表明考虑斜支承影响的研究对象多为板，未曾见到考虑斜支承对运动薄膜稳定性影响的研究。本文综合考虑了非均匀张力以及斜支承对运动薄膜振动特性的影响，对其进行研究。本文通过直角坐标系与斜坐标系的转化，建立斜坐标系中非均匀张力作用下斜支承运动薄膜的运动微分方程，并采用微分求积法求解得到运动薄膜的无量纲复频率，分析变张力系数以及斜支承角度对运动薄膜横向振动的影响。

1 建立运动薄膜运动微分方程

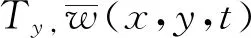
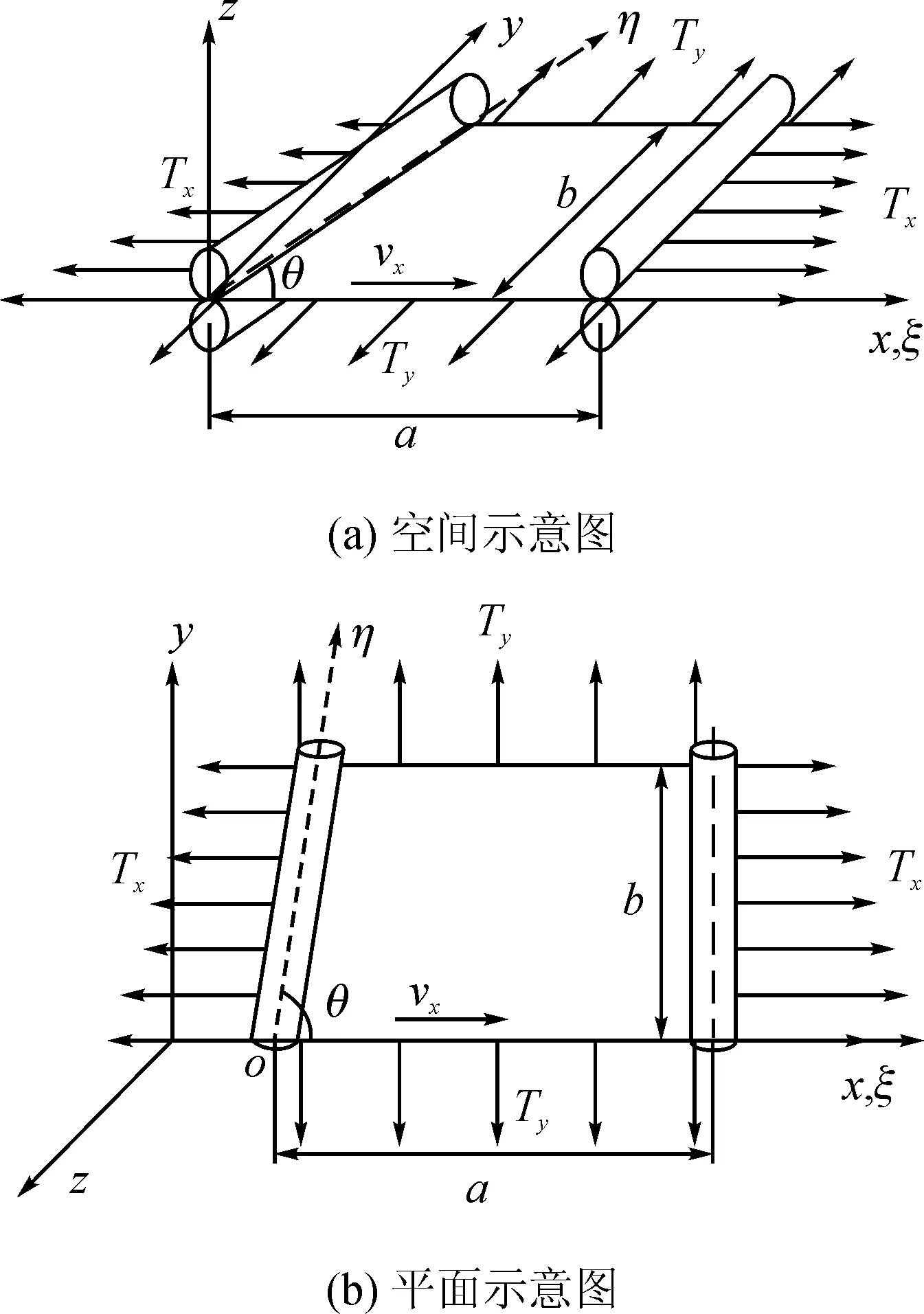
图1 非均匀张力下斜支承运动薄膜力学模型Fig.1 Mechanical model of a moving membrane on oblique supports subjected to non-uniform tension

Tx沿y方向的变化规律为：

(1)

式中：β为非均匀张力系数。

令薄膜在z轴方向所受的外力为F(x,y,t)，由d’Alembert原理可知当非自由质点受到约束时，其主动力F以及约束力FN，与虚加的惯性力FI=-ma之和为零，即F+FN+FI=0，由此将动力学问题转化为静力学问题进行分析[17]。则基于d’Alembert原理得到运动薄膜的横向振动微分方程为：

(2)

坐标转换函数为：

ξ=x-ycotθ,η=ycscθ

(3)

令F(x,y,t)=0，将式(3)代入式(2)得到斜坐标下的运动薄膜横向振动微分方程为：

(4)

引入下列无量纲量：

(5)

式中：c为无量纲速度；r为长宽比；λ表示长度方向与宽度方向的张力比；τ表示无量纲时间。

得到无量纲方程为：

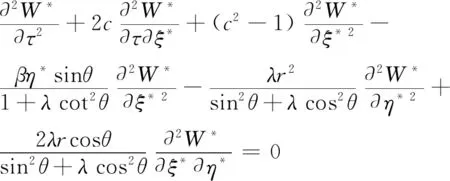
(6)

设方程(6)的解为：

W*(ξ*,η*,τ)=W(ξ*,η*)eIωτ

(7)

将式(7)代入式(6)，得到非均匀张力作用下斜支承运动薄膜的运动微分方程为：

(8)

薄膜四边简支边界条件为：

(9)

2 离散得到系统复特征值方程

应用微分求积法对所得薄膜运动方程(8)求解，将薄膜区域划分为N×N(N=15)个节点，应用δ法将四边简支边界划分为：

(10)

函数各阶偏导数值为：

(11)

由Lagrange插值公式得到一阶权系数为：

(12)

由此得到各阶权系数为：

(13)

根据微分求积法得到运动薄膜的复特征值方程为：

(14)

根据微分求积法可将边界条件离散为：

(15)

合并方程(14)与(15)得到系统特征方程为：

|ω2R+ωG+K|=0

(16)

式中：

K=[Kij]，其中Kij为：

(17)

3 数值分析

本文以陕西北人B624卷筒纸印刷机的基本参数为例，对变张力作用下斜支承运动薄膜进行横向振动特性的研究，取薄膜张力T0=90 N/m，Ty=90 N/m，薄膜面密度ρ=0.12 kg/m2。

当β=0，θ=π/2时，非均匀张力作用下斜支承运动薄膜的振动方程退化为均匀张力作用下直辊支承运动薄膜的振动方程。取无量纲速度c=0.164,张力比λ=0.2,长宽比分别为r=1和r=2，计算运动薄膜振动无量纲复频率，将本文解与解析解[18]比较，见表1。取无量纲速度c=0.16,长宽比r=1.8,张力比分别为λ=0.1和λ=0.5，计算运动薄膜振动无量纲复频率，将本文解与解析解[18]比较，见表2。

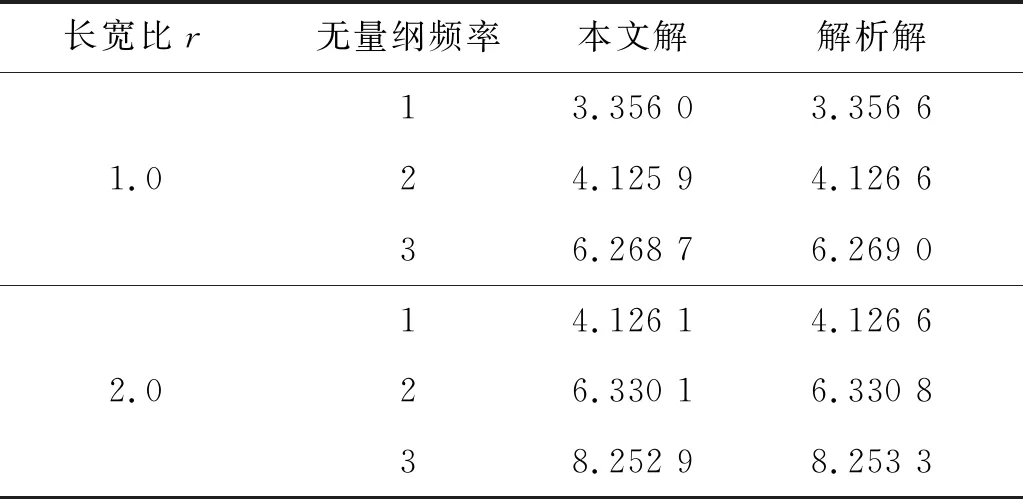
表1 无量纲频率本文解与解析解[18]对比(c=0.164,λ=0.2)Tab.1 Comparing the solutions of dimensionless frequency in this paper and the analytical solution (c=0.164,λ=0.2)

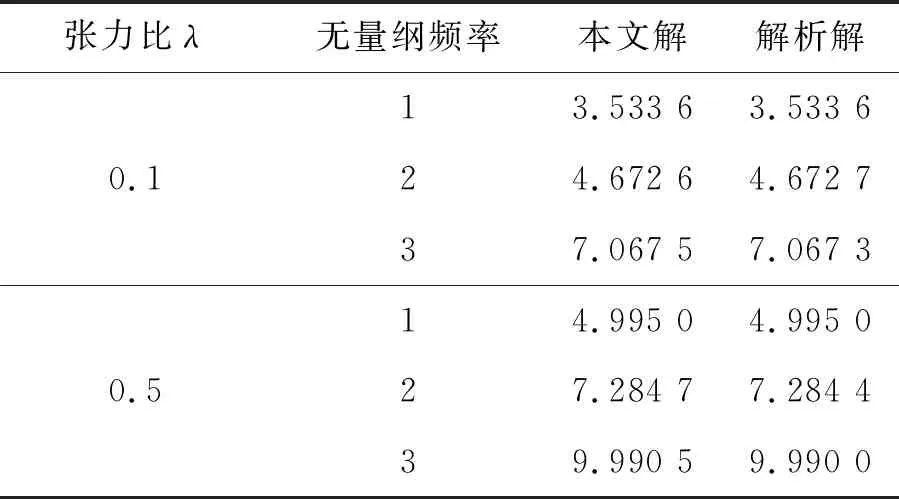
表2 无量纲频率本文解与解析解[18]对比(c=0.16,r=1.8)Tab.2 Comparing the solutions of dimensionless frequency in this paper and the analytical solution (c=0.16,r=1.8)

由表1和表2可知，采用微分求积法求得的频率解与解析解有很好的一致性，且精度很高，表明使用该方法研究非均匀张力作用下斜支承运动薄膜的振动特性可行有效。

3.1 非均匀张力系数对运动薄膜振动特性影响

图2，图3和图4为斜支承角度θ=π/3，张力比λ=0.3，长宽比r=0.5，非均匀张力系数分别为β=0.1,β=0.4和β=0.8时运动薄膜无量纲复频率与无量纲速度之间的关系曲线。

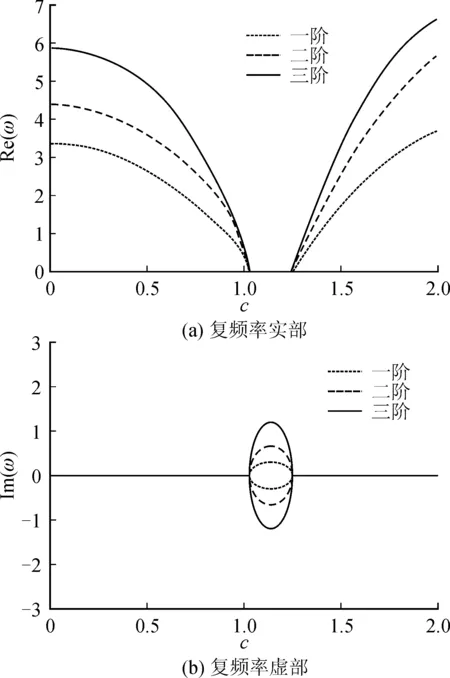
图2 无量纲速度与无量纲复频率关系曲线(β=0.1)Fig.2 Relationship between the dimensionless speed and dimensionless frequency (β=0.1)

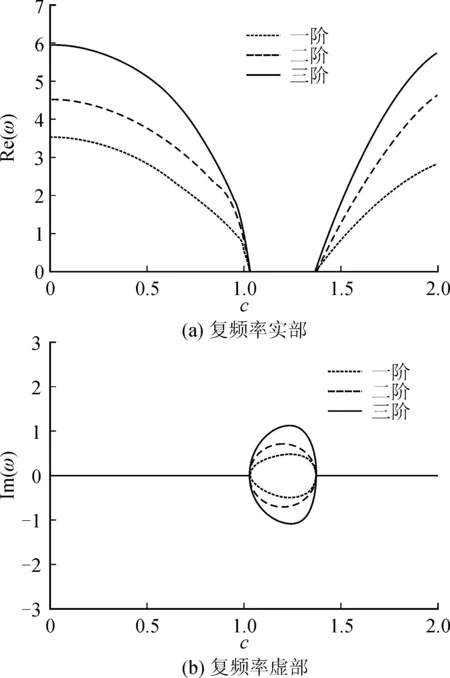
图3 无量纲速度与无量纲复频率关系曲线(β=0.4)Fig.3 Relationship between the dimensionless speed and dimensionless frequency (β=0.4)

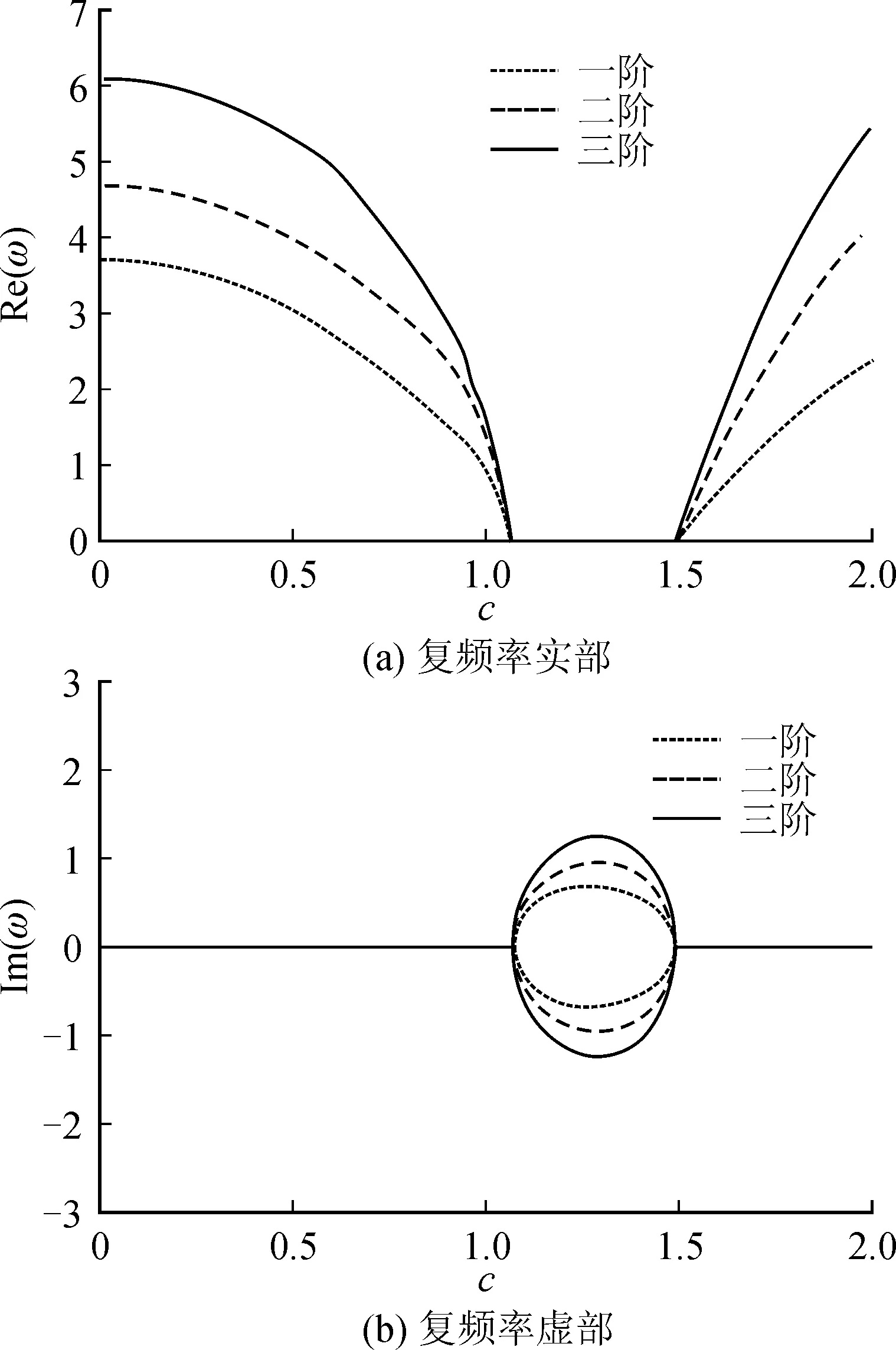
图4 无量纲速度与无量纲复频率关系曲线(β=0.8)Fig.4 Relationship between the dimensionless speed and dimensionless frequency (β=0.8)

图2为非均匀张力系数β=0.1。当01.25时，运动薄膜前三阶模态又重新稳定。c=1.03为系统的无量纲临界发散失稳速度，对应薄膜工作的实际临界速度为v=28.7m/s。

图3为非均匀张力系数β=0.4。当01.37时，运动薄膜前三阶模态又重新稳定。c=1.04为系统的无量纲临界发散失稳速度，对应薄膜工作的实际临界速度为v=29.0 m/s。

图4为非均匀张力系数β=0.8。当01.49时，运动薄膜前三阶模态又重新稳定。c=1.07为系统的无量纲临界发散失稳速度，对应薄膜工作的实际临界速度为v=29.8 m/s。

由上可知随着非均匀张力系数的增加，系统工作的临界速度增大。当无量纲复频率实部为正，虚部为零时，系统处于稳定状态；当虚部出现，实部为零时，系统是不稳定的，而系统临界速度就是无量纲频率实部和虚部均为零时所对应速度，所以系统工作的临界速度增加时，系统稳定性增强。

3.2 斜支承角度对运动薄膜振动特性影响

图5，图6和图7为非均匀张力系数β=0.1，张力比λ=1，长宽比r=2时运动薄膜斜支承角度分别为θ=π/4,θ=π/3和θ=5π/12时运动薄膜无量纲复频率与无量纲速度之间的关系曲线。

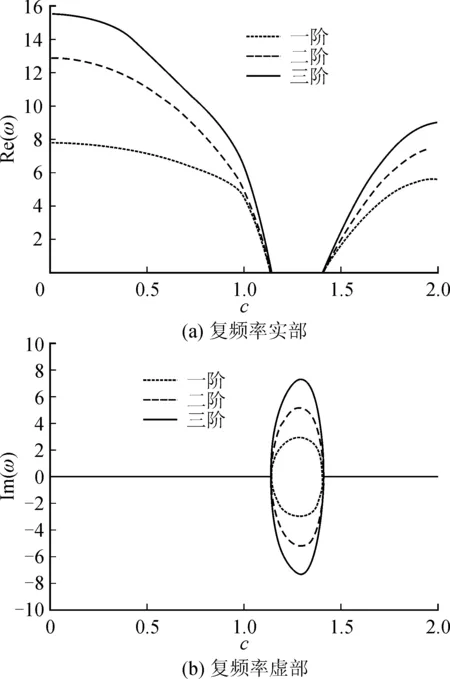
图5 无量纲速度与无量纲复频率关系曲线(θ=π/4)Fig.5 Relationship between the dimensionless speed and dimensionless frequency (θ=π/4)

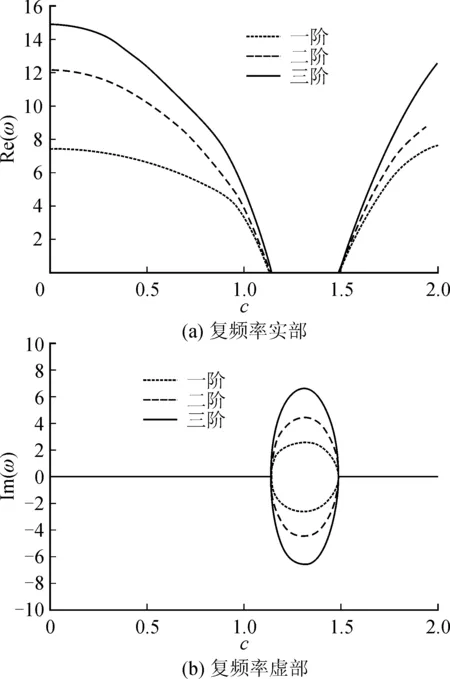
图6 无量纲速度与无量纲复频率关系曲线(θ=π/3)Fig.6 Relationship between the dimensionless speed and dimensionless frequency (θ=π/3)

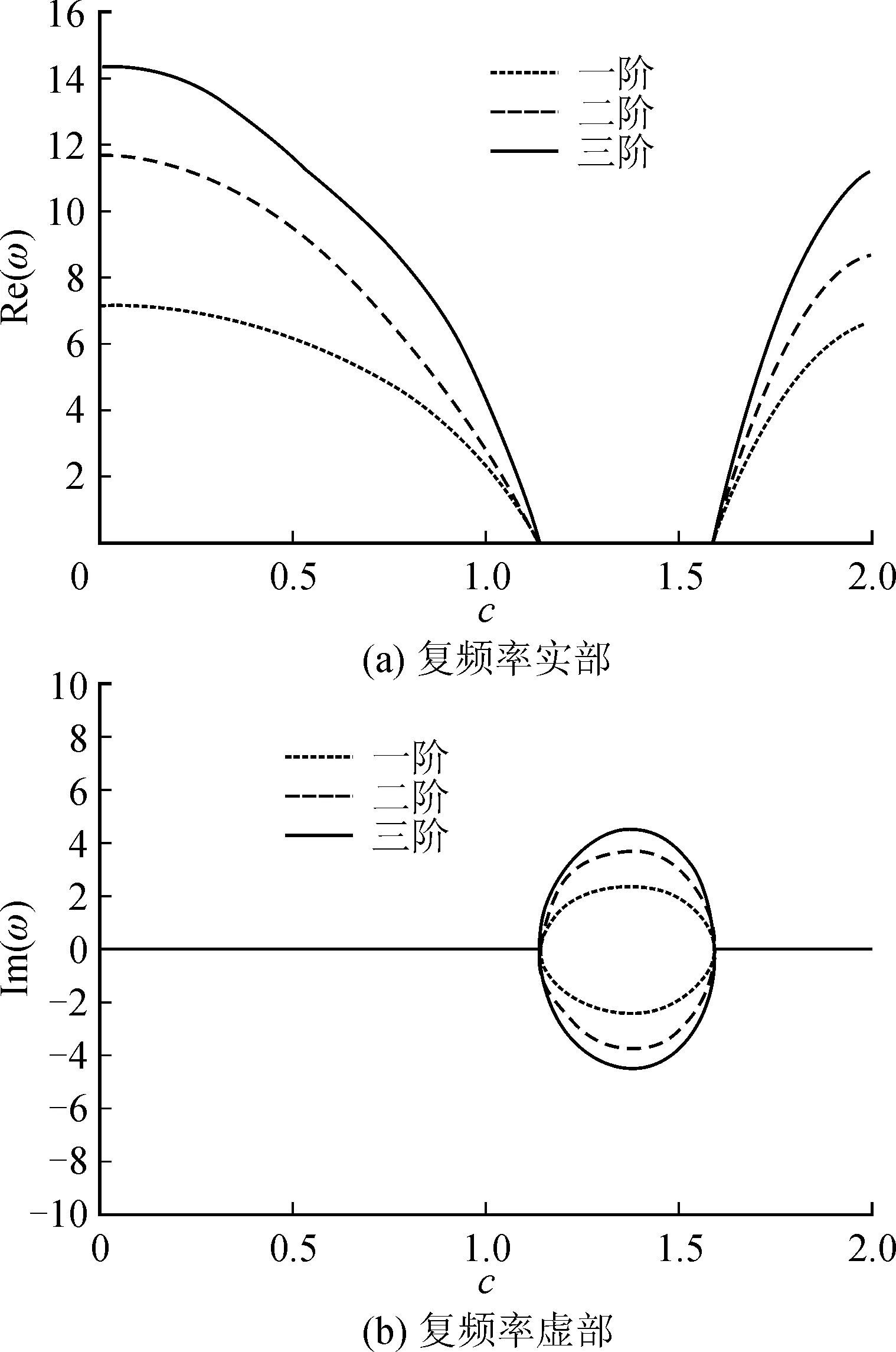
图7 无量纲速度与无量纲复频率关系曲线(θ=5π/12)Fig.7 Relationship between the dimensionless speed and dimensionless frequency (θ=5π/12)

图5为斜支承角度θ=π/4。当01.41时运动薄膜前三阶模态又重新稳定。c=1.14为系统的无量纲临界发散失稳速度，对应薄膜工作的实际临界速度为v=32.9 m/s。

图6为斜支承角度θ=π/3。当01.49时运动薄膜前三阶模态又重新稳定。c=1.14为系统的无量纲临界发散失稳速度，对应薄膜工作的实际临界速度为v=31.8 m/s。

图7为斜支承角度θ=5π/12。当01.59时运动薄膜前三阶模态又重新稳定。c=1.14为系统的无量纲临界发散失稳速度，对应薄膜工作的实际临界速度为v=31.3 m/s。

由上可知随着斜支承角度的增加，系统工作的临界速度减小，系统不稳定区域增大。运动薄膜的斜支承角度对系统稳定性有重要影响。

4 结 论

本文以陕西北人B624卷筒纸印刷机为例，采用微分求积法对非均匀张力作用下斜支承运动薄膜的横向振动特性进行研究，得到以下结论。

1)随非均匀张力系数的增加，系统稳定性增强。当非均匀张力系数分别为β=0.1，β=0.4和β=0.8时，系统工作的临界速度v分别为28.7 m/s，29.0 m/s和29.8 m/s。

2)随斜支承角度的增大，系统稳定性减弱。斜支承角度分别为θ=π/4，θ=π/3和θ=5π/12时运动薄膜实际工作中的临界速度v分别为32.9 m/s，31.8 m/s和31.3 m/s。适当减小运动薄膜的斜支承角度可有效保障系统的稳定性。